On Weyl-Dirac gravitation theory and its development

More than a century ago, in 1918, G. Weyl proposed a theory of gravitation based on local symmetry with respect to the gauging of measurements [1]. The original idea of G. Weyl was the geometric unification of gravity and electromagnetism. In 1918, G. Weyl generalized Riemannian geometry. This generalization was called Weyl geometry. The action had the form:

S w

/ d ⁴ 色 J 1 det g | • L w /w = 户 ² - 产理亦 "" ,

(.1)

where R is a Weyl curvature of a space-time (different from Riemann curvature), F^ is a strength of the electromagnetic field, ® is a parameter of the theory. In case of local changes of a scale, the value of the Lagrangian density ^- ^ • L w stays invariant. The vector of the electromagnetic field A ^M was subjected to a gauge transformation taking into account a change in the scale, leaving unchanged the value of ， - ^ • F^ F 『 Let us note that this value is invariant for dimension 4 of space-time only.

In its original form, integration of gravitation and electromagnetism appeared to be incompatible with observations and enlarged the collection of inviable theories of gravitation. The basic objections against Weyl theory are given in the famous review on gravitation by V.Pauli [2]. Since the original Weyl theory did not satisfy astronomical observations and contradicted quantum theory, it was abandoned.

Now it is recognized that Weyl vector Л ^л as a part of both strength F ^“ and geometric connection Г 頂 cannot be of electromagnetic origin. Nevertheless, the ideas of using a quadratic term of curvature in gravitational Lagrangian, as well as a compensating vector field in geometric connection in order to preserve the local scale invariance of the action, are still of interest today.

According to E.Sholtz [3], let us briefly describe further research. In the middle of the 20th century, the interest to Weyl’s ideas renewed as it was understood that local scale transformation can play an important role in physics. Different groups of physics brought their attention back to Weyl’s ideas 40 years later: Omote, Utiyama, Dirac, Kanuto, Pirani et al. [4] - [8].

In the beginning of 1960s, Carl Brans and Robert Dicke proposed a modified relativistic gravitation theory with non-minimal connection with scalar field [9]. This theory allowed consistent introduction of a variable parameter of the intensity of gravity. Brans and Dicke developed a theory of gravitation, which, with a certain choice of parameter, corresponds to a special case of the theory of gravitation with Weyl geometry of integrable type. Then many authors, in the spirit of Weyl’s ideas, introduced a scalar field connecting gravity and particle physics into their models.

The fundamental paper by Dirac [6] develops a new approach to the Weyl gravity. Dirac used Weyl geometry that had been forgotten by physics by 1970s. Dirac followed Eddington’s notation and terminology of geometric covariants and invariants for scale-covariant fields.

Dirac introduced a very important concept of the scale-covariant derivative for large-scale covariant fields into the arsenal of Weyl geometry. Besides, the same as Brans and Dikke, Dirac introduced a fundamental scalar field into the theory and marked it with p. Dirac connected this /3 field with gravitation in a non-minimal way.

In the 1980s, the interest in local scale transformations in gravitational physics began to intersect with the study of the mechanisms of mass generation in elementary particle physics [10], [11]. In addition, alternative theories of gravity based on Weyl geometry began to be used to solve the problem of the origin of dark matter and dark energy [12].

The problems of cosmology caused some interest to conformal versions of gravitation with a scalar field. As a result, Weyl’s approach to the description of the gravity in the 21 “ century has gained the second wind. Here, we can mention the papers by Nathan Rosen and Mark Izraelit [13], and detailed reviews by Erhard Scholz [3], [14].

Russian author also contributed to the research on scale invariant gravitation theories. Here we can mention the works by K.P.Stanyukevich, V.N.Melnikov et al [15].The publications by M.V. Gorbatenko, A.V.Pushkin and Yu.A. Romanov [15] - [18] describe an approach close to the works of Kanuto [7].The work by A.T.Filippov offers the models of affine gravitation on the basis of Weyl ideas [19].In the publications by O.V.Baburova and V.N.Frolov the space-time is attributed with a geometric structure of Kartan–Weyl space with the curvature, torsion and nonmetric properties of the Weyl type with the scalar Deser-Dirac field [20]. In the works of V.A. Berezin, V.I. Dokuchaev, Y.N. Eroshenko, cosmological models based on Weyl geometry are developed [20], [21].

During the last five years different alternatives to apply Weyl (local) conformal symmetry towards gravitation are considered from the point of view of modification of the general theory of relativity (GR) for describing dark matter, dark energy, evolution of early Universe. Modifications of the GR on the basis of the local conformal invariance has been studied for a long period of time as the attempts to solve different problems. In particular they search for the ways to do renormalization in quantum gravitation, consider consequences of renormalization of the energy-momentum tensor, and study the dynamics of the inflation in the early Universe and origin of mass for elementary particles.

Currently, there are many researchers dealing with different versions of gravitation based on Weyl geometry. The number of publications is currently increasing. As some examples we shall mention such authors as Philip Mannheim [23], [24], Ichiro Oda [25], [26], Israel Quiros [27], Beltran Jimenez [28], Carlos Romero [29], Dimitru Ghilencea [30], Tiberiu Harko [31].

Here, we shall focus only on Weyl-Dirac gravitation theory.

• A.    Weyl geometry

The subject of Weyl geometry is a differential manifold M with a set bi-linear non-degenerate differential 2-form (metric function) g and differential 1-form / . This geometric object is called Weyl space, it can be marked as ( M, g, A ) . We shall specify a particular signature of metric g . A new thing as compared to Riemann geometry is introduction of additional 1-form A . This 1-form is closed if dA = 0 , and is exact if there is such 2-form ст, that A = do . Here, d is the operator of exterior differentiation.To put it short, an exact form A corresponds to the case when vector A _a can be represented as a gradient of some scalar A _a = 今? . A closed form corresponds to the case when 凡户 = 历^ — d| ^ 三 0 . In a general case of Weyl geometry A is not a closed form.

Weyl (local scale) transformation is set with ratios:

g T g = Q ² • g , A т A = A - d log Q

(A.1)

where Q is a strictly positive differential real function. In the coordinate form, it looks as follows:

9 叩 ⑺ т g^ ⑵ =Q ² ⑵ • g p," ⑵ , Q(t) = ехр(ст( т )) , (A.2) do

^A p ^{T A} p = ^A p - d^ p = ^A p - ▽ н ^{с, с} = ^lnQ ( £ ) . (^A ・ 3) Here, the transformed quantities are marked with a wavy line above. Coefficients of Weyl connection Г is found with metric g ^© (t) and Weyl vector A " (t) . In the coordinate form, they look as follows:

ГP" = уgXa (dpg@" + d"g@p - d@gH") = ГР" + *A" + 6)Ah - gp"A% , where

%ga© = (dp + 2Ap) g@户, rP" = 2g"“(％g。" + d"gap - %g“")

Here gamma’s are regular Christoffel symbols of connection of Levi-Civita. A convex line above shows Weyl analogues of the quantities of Riemann geometry.

A condition of non-metric property for the metric tensor in the case of Weyl geometry is:

j 入 g @户 = ^{- 2}&g @户

(A.7)

▽ 入 is defined similarly in a general case with replacement of Levi-Civita connection with the Weyl one: Г for Г . Let’s remember that metric conditions are valid for Riemann space

V _A g _a© = 0 .

(A.8)

Number к = W ( К ) is called Weyl weight of the geometric quantity H ;it is the degree in the Weyl transformation:

H T H = Q * H.

(A.9)

Weyl covariant derivatives are determined as follows in the general form for scalar h, vector h _a and tensor h &B :

D ^ h(x) = 仔丛 + W ( h )4j h ( r ) = d p. h (吟                    ( A.10)

D ^ h _a 三[乙 + W ( h 。 )/ ] h _a ,                          (A.11)

D ^ h _ap 三[乙 + W ( h °0 )4] h*                      (A.12)

Geometric quantities that get transformed with Weyl weight W are called Weyl covariants, and if W (H ) = 0 , then they are Weyl invariants. The action for the Weyl gravitation S should be Weyl invariant: S = S . Lagrangian of gravitation L respectively should be Weyl covariant with weight W ( L ) = - 4 , since W ( J | det g |) = 4 , and

S g = / d ⁴ £ J | det g | • L g .

~.

(A.13)

Let us note that spaces ( M, g, A ) and ( M, g, A ) coincide up to isomorphism a Weyl transformation, i.e. a local scale transformation does not change Weyl space. All examples of ( M, g, A ) are equivalent. They are joined in the class of equivalency with regard to gauge Q . Real physical space-time ( M,g i ,A i ) is unique with regard to the choice of gauge, i.e. among the set of all Weyl equivalent examples from the class of ( M, g, A ) one example is separated at a fixed gauge function Q = Q i . In this case, we shall say that Weyl invariance is violated. Such violation is related to the fact that in physical gravitation the scales of time, distance and mass are well-defined. Let’s point out that in the case when A is the exact 1-form in the object ( M, g, A ) , we can select gauge Q in such a way that A * will turn to zero on the all space M :

Эст

^A * ^{T A} * = ^A * -      = 0 .                            (^A.14)

дт ^

Such Weyl space is called an integrable Weyl space. For integrable Weyl geometry A = de . Object ( M, g, de ) is called in the references as IWG (Integrable Weyl Geometry) or WIST (Weyl Integrable Space Time).

• B.    Weyl-Dirac Theory

The action of Weyl-Dirac gravitation is written as follows:

S。= - M2 / L^ V^d4, = - + / L0 V^d%, where Lagrangian L。is written as:

or

And the strength of vector A ' :

F^" = %A“ - 瓦丄.

Let us introduce an ordinary matter. Its presence can both preserve Weyl symmetry (electromagnetic, radiation) and violate it (baryon matter). Equations of motion are obtained by varying the action by metric Bg ^" , by field 8/ and by vector SA " :

£"" - 1 g“"金三 G“" = T“" = T(。)“" + T(Q“" +T(F)h" + 8亓7(：)“" - g""* /2 (,)  ,

2'

where

T ⑻"一   ( - 2+ 2 ) .严伝歹 + &  (2 - a ) 夕"- g 产 / •瑞 + m //" ,

T ⑷ "" =( a - 6) ( T5 + 哆 4 Х 人) + "-^ 俨 4 " + /3 " 4 " - g "" //)

(B.6)

(B.7)

T (尸)""

87r

F

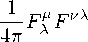
部 [2 产 ^ғ ^а-

2F " F "X ,

(B.8)

T ^(m) "" is the tensor of energy-momentum of regular matter. Quantities T ^(m) "" , ^ and J " are parts of the expression for variation of Lagrangian L _matter of the regular matter:

〃 ⁴“ j^0Mte

,

(B.9)

8 ( b _matter V- ^ ) = ^{8 7T} ( * "" 5^ _Д" ^- ^ + 16 7J Х 8 厶 ^- ^ +w83 ^- ^.         (B.10)

This density of the Weyl charge of the regular matter and the density of the Weyl current of the usual matter. Variations by field 83 give the following equation:

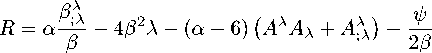
(B.11)

Variation by vector 84 " gives the equation:

4 ® ² F "" = I6 7J " - 2( a - 6) 3 ( 3 " - 34 " )

(B.12)

Let us say some words about different gauges.

As it follows from the equation for function 3 (B.11) when parameters A >  0 , a = 0 , W = 0 , the following ratio is valid

3 ² =-石冗                              ( B.13)

With replacements of this value in the Weyl-Dirac operation, we get:

S /

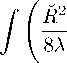
— G

² F "" F "" 丽 d ⁴ ,,

(B.14)

That is we get Weyl gravitation action.

If we put 4 ^X 三 3 ^X , then we get integrable Weyl geometry, and F "" = 0 .

If we put 3 = 1 , then conformal symmetry gets violated, and Weyl-Dirac operation complies with GR operation; but there is a small detail — when F "" = 0 , the geometry of space-time will not be the Riemann one and there will be the ”second clock effect”.

• C.    Problems of Weyl-Dirac theory

• 1.    Weyl vector 4 ^X as a part of Weyl connection can’t be associated with electromagnetic potential B ^A . Let us emphasize that unlike electromagnetic potential Weyl vector 4 " acts on the particle not only due to the Weyl charge available and non-zero strength, but also as it is via Weyl connection.

• 2.    As Albert Einstein noted, existence of sharp spectral lines in the radiation from stars is impossible in space-time described with non-integrable Weyl geometry due to the fact that the velocity of travel speed of the atomic clock depends on its past history or, in other words, two clocks that have travelled in the Universe in different ways and come back to the initial point will have different rate speed (the ”second clock effect”).

In fact, if Weyl vector 4 ^X is a vector of electromagnetic potential 8 ^X , it will be a part of electromagnetic connection and then you have to differentiate two metrics 曲* and ds ^ . Metric df * is connected with gravitation and electromagnetism equations, and metric ds ^ is connected with the distances measured in atomic physics and elementary particle physics. It is not natural, as Albert Einstein noted [2]. Besides, the development of quantum mechanics has shown that electromagnetic potential B ^A is connected with a compact group of transformations of the field phase and so it is a part of ”long derivative” as ieB ^X , that is with a multiplier in the form of an imaginary unit. Vector 4 ^X is connected with a noncompact group of length scale transformations.

Weyl geometry results to two types of geodesic lines – invariant and covariant. Covariant geodesic lines can be interpreted as extremals of action for the point particle with a variable mass. Equations of free motion, respectively, for a point particle in Weyl geometry contain an additional term that can be called a specific Weyl force.This term changes the scale of the mass until violation of conformal invariance, but after the local conformal invariance is violated, it results into real changes in the mass of a physical particle.

A violation of the conformal invariance implies the choice of a particular example of Weyl space from the class of equivalence with regard to Weyl transformations.

Change of the 4-momentum of p ^M classical Weyl particle is defined with equation

午 + 丄Г*讨犷=m 4X + qw • F^   , as m ““ where dxa

卩入=mux ,  ua = ——, ds = ,|д@/зdxadx^ |,   luaual = 1 ,  W(u) = —1, qw is Weyl charge.

In a non-relativistic case the change of the momentum is △万 = △ (mv) = m • △不 + A m • ^

In a non-integrable case in the loop at 写 =0 the change of mass A m takes take place for the mass point mass point. This is also a manifestation of the so-called ”second-clock effect”. Our interpretation of the mass change is based on parameterization set with expression (C.2), which is most close to the parameterization of geodesic lines in the general theory of relativity.

We note that manifestation of the ”second-clock effect” can be interesting as the way to change the mass of the particle when going through microscopic areas of nonzero strength F 、 of Weyl vector 4 . But such change of the mass surely must be a discrete one; that is the field of the Weyl vector and its strength must be quantum. Besides, such a possibility should not contradict experimental facts and general concepts of particle physics.

Some authors use the gradient of scalar function В instead of the Weyl vector in geodesic lines despite the fact that there is a nonzero strength 乙户 of Weyl vector Л ^л in the Lagrangian. In our opinion, it is inconsistent option. Of course, it allows getting rid of the”second-clock effect”, but it does not correspond to the spirit of the Weyl geometry.

• D.    Solving the problems of Weyl-Dirac gravitation theory

In a non-integrable case of the Weyl vector,we offer two ways out. In particular, these methods are as follows:

• 1.    a non-integrable Weyl vector has small norm at the macroscopic scales, and changes chaotically, so averaging by vector field results in some stochastization of the motion of the particle;

• 2.    a non-zero value of the Weyl vector is only in the area of Plank scales, in analogues of vortons– vortex rings. And here the change in the mass of other particles at interaction with Weyl analogues of vortons happens in a discrete way.

• •    Method 1. Stochastic Weyl vector. Let the influence of random Weyl vector field Л ^л on the motion of the particle be rather small, the field of vector Л ^л itself does not have preferential directions and is isotropic. Let us consider the equation of particle motion in compliance with covariant Weyl geodesic line

duH + г^n°^ • ds = - [(/%a) wA - Лл] • ds(D.1)

Let us consider value

产=-(4入-(Ааиа)仆)(厶-(Ааиа) и力=(Аапа)2 - 4入4.

This value is invariant. So, we can introduce density distribution of the normal type for random value g =，-5W (a0 At ⑵ А；⑵, where А^ = A入一(Ааиа) • u入.

Let’s introduce Lagrangian equation with the proper time of the particle d丁 = ds, duH + Г^^uau^ • d丁 = стА^ • dr,   〈А)(丁)〉= 0 ,   〈А)(丁i) • А丄〃(丁2)〉= -ст2 •心• 8 (丁i - 丁2).

(D.4)

We get an equation that describes Brownian process. In fact, there is fluctuation around classical GR trajectory.

• •    Method 2. Tubes of weylons. Let us assume that the field of Weyl vector at quantization results to very massive particles - weylons [13]. Weylons interact with usual particles at very small distances. Let us consider non-relativistic motion of very heavy weylons. If weylons form structures as closed, chaotically directed tubes, then we see analogue with superfluid vortex lines in helium. It would have been more realistic to consider a model of vortex threads in the form of vortons analogues.

With the chaotic orientation of these vortons, the average contribution to the change in the mass of particles when passing through a region of vortons is zero. If the mass of the weylon is close to the Planck mass, then the processes of particle scattering on the vortons are significant only at small (Planck) distances. In that case, the ”second-clock effect” at macroscopic distances is not observed, and at small (Plank) distances the particles should be described with quantum theory and can change the mass in discrete way interacting withweylon. So, these vortons that are analogues to rotons. These processes could take place at the early stage of the Universe existence at very high energies.

• •    Method 3.Integrable Weyl Geometry (IWG). Let Weyl vector А in defining Weyl space (M, g, A ) be equal to the gradient of scalar function:

4 — %/( a )

(D.5)

“ =/   ， where p(x) is Dirac function. Let us introduce another vector, CM(a), that changes the same way as Weyl vector А* in Weyl transformation:

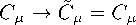
d In Q( x ) dx ^H

(D.6)

Then modified Weyl-Dirac Lagrangian takes the form:

丄 mod = / 2 冗 + 6&H + q 回 -& • / ) •(严- 。匕 / ) + 2 入炉 + ® ² E ^h" %" ,      (D.7)

There is the strength of vector C 入 in the Lagrangian:

E q"

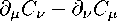
(D.8)

and Weyl vector Л ^л is not a part of the Lagrangian any more, and number 6 is not subtracted from q . Let us emphasize again that A _M and 。 丛 are completely different vectors. Exactly vector 4 is used in defining Weyl connection:

Г 頂 =г 書 + 心 4 + 心 4 S' ・

(D.9)

• Accounting for the electromagnetic field. Let us introduce a complex field g . And let us introduce a complex gauge Weyl vector w that combines real vector C (related to the changes in the norm of field g ) and real electromagnetic potential В (related to the changes in the phase of field g ) :

w = C + 分 В.

(D.10)

An electric charge is included in the electromagnetic potential vector В . Let us introduce the expression for the complex scalar field:

д ( т ) = tr ( £ )• exp ( 勿 • 〃 ( £ ) ) .

(D.11)

Then we can define the complex invariant Weyl derivative:

^d “ g = %g - ^w “ • g = (号 - ^C j x + * ( 〃 “ - ^В “ ) x ・              (D.12)

E. Modification of the Weyl-Dirac theory of gravitation

Taking into account all the comments made, we formulate a modified model of gravitation close in

spirit to the Weyl-Dirac gravitation.

Modified model. In our model there is a real dilaton field / ( £ ) , a complex scalar field g (: r ) , a real

vector C ^ ( x) , electromagnetic potential В ^ (x). Let us introduce dimensionless parameters q , 閥 ， 入 , 夕 ， £ ,

J, 8 2 . Action

Sb 屮 =--2^ / c^x^- g • 丄 /g .

(E.1)

The Lagrangian of the model gets written as:

Z /g = 斤金 + 6 丛俨 + ag “" 仇- C “ • /3) •仇- C “ • /3) + 〃 ( gg * - “ 斤) 2

+2 X/3 ⁴ + £g “" (％ g ^— (^c h + * ^В д ) • g ) * • (^d“ ^一 ( ^C “ + 〃 ^В “ ) • g )               ^        (E.2)

+ 8 2 H" Я д. + JE H" %”

Affine connection is written within the framework of the integrable Weyl geometry (IWG),that is Weyl

vector is gradient:

—d3 "

—~.

(E.3)

Before the violation of conformal symmetry, the mass of the particles depends on the dilaton field: m = m o • 3 ( x ) . The strengths of vector fields C and В , generally speaking, are nonzero:

^E H"

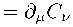
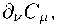
Я д"

д _м В " - d " В д .

(E.4)

In this model, the vector C also transformed by local conformal transformations as the Weyl vector A gH" ~^ 行H" = C (x) • gH"

4 T(

d In Q( x ) dx ^H

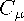
d In Q( x ) dx ^H

(E.5)

but does not coincide with it. This property allows getting rid of the ”second clock effect”.

In model (E.2) you can replace scalar g with a doublet of the Higgs field: g ( x ) T Я ( x ) , as well as add interaction with fermions. You can also enter gauge fields.

Let us note that vector C 入 after fixing the gauge of 3 = 1 satisfies Proca equations [13], and can be studied as a component of the dark matter. Constant Л in Einstein equations comes from the term 2 入 3 in the Lagrangian (E.2), and can be a source of dark energy.

• F.    Violation of conformal symmetry in Weyl-Dirac gravitation

In the real Universe, the symmetry of the gravity equations with regard to local scale transformations of the metric is violated; the mass scale is fixed at the atomic level and the level of elementary particles. So, here comes the question: What is the ”right” way to break this symmetry?

• 1.    It can be broken ”manually” ， by putting / ( £ ) = 1+ £ ( £ ) , | f ( £ ) | <<  1 . Many researchers did that, including Dirac, Rosen, and Israelit.

• 2.    You can try to come up with a mechanism for spontaneous breaking of this symmetry, combining it with the Higgs mechanism of mass generation in particle physics.

• 3.    Note that its ”natural” violation occurs due to quantum corrections. We will consider this mechanism further in more detail using an example.

As an example, we shall further consider conformal invariant operation with Dirac field /3 and real scalar massless field g:

S 3 屮 = - 歳 / d⁴x ^- g { R • ^{3 2} + 6 g “" 廿凤

(F.1)

+2* /3 ⁴ + 2“ 9 ⁴ + 金 g "" (% 9 - % • 9 ) • ( ^d" - ³ f • 9 ) }

• •    The first type of quantum corrections. This kind of quantum corrections is related to the fact that the term 2 A ^ • g ⁴ changes taking into account quantum fluctuations. We will interpret field 9 in a quantum way by introducing classical parts of the field g _quant = 9 + A g , where A g are quantum fluctuations. If the classical part of the field is nonzero, then a replacement should be made [32]:

  ² 儿 ^{g 4} T ² 儿 ^{g 4} • J   9% [RU + ^Rg 2

  
  

  1 + ( s - 1) •

  
  

  ( ¹ -符 ]n { 晉 }) 3

  
  

  (F.2)

  
  

This type of corrections does not violate Weyl invariance if we introduce an additional conformal -invariant field for cutting mass M ⑺ 〜 3 ⑺ .

If we turn to splitting the potential

2A^g4 T 2A^ ^92) 92, then we can put〈92〉〜 32(£). So, there is a way to avoid the violation of the local scale symmetry for the first type of quantum corrections.

• •    The second type of quantum corrections. Vacuum polarization takes place in a strong gravitation field, and the trace of the energy-momentum tensor of the quantized field 9 receives quantum additives. Let us note that value 帆审 ) = 舄| ) is Weyl invariant. Let ^ = 0 . Nevertheless, there are additives due to quantum fluctuations in field “ • The vacuum state | 0 >  should be taken for the field 9 = /3“ ， and consider the renormalized energy-momentum tensor 〈 0 ] !} ( " ) 〃 I 0 )   =

ren

〈0 I/32^/(^)^I 0〉   , taking 3 as a classical quantity. Let us note that 3 function should not be quantized as it is a part of geometric connection (D.3), (40). Besides, the function is strictly positive 3(T)> 0 , and vacuum state with 3 = 0 is not determined for it. We presume field 3(£) as non-physical dilaton field.

Let us provide an expression for anomalous trace of the energy-momentum tensor (see [33]):

T*)»

(e • С °з,б С ^a3 ^ ^s + 6

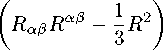
+ cR + d •

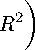
\      / ren = _______

8 ^     = 2880*

where С зз^ is Weyl tensor, 6, c, d, e are numerical coefficients.

Unsteady-state isotropic metrics of FLRW with conformal time 〃 ：

{sh(r), к = —1 ] sin(『)，k =+1 ，   , r, к = 0 J result into the equation for / as follows (see [15], [34]):

/'+ к • / — sign(X) •/3 = 0

Here, / ( 〃 ) is determined with the expression with random p(x) >  0 :

/⑺• a⑺=/詮/e).

² |

Accounting for quantum corrections of the second type, we get:

/ + к • / — s® ( 》)•尸 =У|Й • 0 3 2^ ( б (友 0 岁。— 3 炉) + cR + d •露) . ( F.7)

Anomalous quantum additives have appeared that violate scale invariance of the initial equation.

• •    Example. Let’s consider a flat case, к = 0 . Then, having taken the values of parameters b = — 1 , c = 6 , d = — 2 from [33], we get here 炉⑺ 三 、：?) ) :

b ( R^R aB — 3 R ² ) + c • 2 R + d • R ² 〜一 岑 • 5 8 / 4 — 232 ( 4 4 / ³ / ( 1 ) 〃 + 10 4 / ² / ( ² ) 〃 ² + 4 4 // ( ³ ) 〃 ³ +58 /⑷〃 ⁴ —( 94 /⑵〃 ² — 16 // ⁽¹⁾ 〃 + 22 / 2 ) / ² /⑵〃 ²

+33 / ² / ⁽²⁾ / ⁽²⁾ 4 ⁴ + 24 / 2 / ⁽³⁾ / ⁽¹⁾ ^ ⁴ — 6 / 3 / ⑷ 4 ⁴ ) .

At / = 1

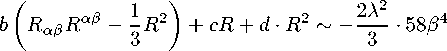
So, the equation for scale factor a ( 〃 ) takes the form:

/ + к ■ / — sign(X _ren ) • / ³ = 0

.

(F.8)

where

》 re 〃 = A ⁺ 1080 ^ ^{( b} - ¹2 ^d )『， /®) = a ⑺， #¹

So, anomalous trace of the energy-momentum tensor (F.7) leads to appearance of derivatives of the function / by conformal time 〃 in Einstein equation.These derivatives explicitly have violated conformity of equations of gravitation with Lagrangian (F.1). However, we have nullified quantum additives containing derivatives of function / over conformal time 〃. To do this, we put / (〃)= const and in such a way fix gauge /. For agreement with GR we put / = 1. We have got rid of quantum corrections in Einstein equations that depend on derivatives:〈0 ІН")”| 0〉 = 0, but cosmological parameter A happened to be renormalized: Aren = A + 上。打(b — 12d) A2.

So, in our opinion, a natural way to violate Weyl invariance is accounting for quantum vacuum corrections for the energy-momentum tensor of different physical fields in the Lagrangian.

• G.    On Mannheim-Kazanas solution

Within Einstein’s standard equations of general relativity, the flat rotation curves of galaxies cannot be explained without the hypothesis of dark matter, the particles of which have not yet been identified. The vacuum centrally symmetric solution of the equations of conformal gravity is the well-known

Mannheim-Kazanas metric (see [23]), on the basis of which these curves have got a purely geometric explanation [24]. In 2017, we showed (see [35]), that the Mannheim-Kazanas metric is a solution not only to the Bach equations obtained from the Weyl conformal invariant Lagrangian, but also the solution of the equations of a simplified version of the Weyl-Dirac theory with a nonzero Weyl vector [16], [17]:

R a/з - у д ^в R = - 2 / @ 4 - д @/ 片 ² - 2 д @//% + ^ _а ； ^ + 4 ； @ + 入⑺ д @/

The solution looks as follows:

,             ..с dR²                         о

曲‘* 2 = - f ( R ) 必 ² + 戸® + R ² [曲 ² + sin ² %，] ,

"*_     1         、,*_》 0 R 0

.zi                                   、，/ A                                        ,

( R o - R )         ( R o - R ) ²

F ( R )- ( 1 - R ) 2 ( 1+ R 0 - %) + 于

This solution can lead to the Mannheim-Kazanas solution

曲2 — — (е7)^к 必2 + (е-7)^к dR2 + R2 [面2 + sin2 %g2], where

⁽ e ⁷ ) ^к ^{— (1} - 3 /) ) - “^{( 2} - ³ "“) ⁺ ? ^R - k^{r 2} . R

To do this, you need to turn parameters /,)，片 into parameters 『 ° , R o as follows:

/

『 0

^{R o} ( 2 + 3 能)

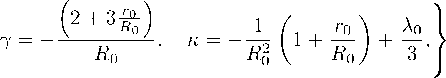
Piyabut Burikham, Tiberiu Harko, Kulapant Pimsamaru and Shahab Shabidi [31] showed that the Mannheim-Kazanas metric is the solution of Weyl-Dirac gravitation equations in the integrable case. Their solution is as follows:

exp( - A ) -exp ( “ ) — 2 / + 『『- ^ 2^¹ + 蝕户

0 2            3      『

It is evident that it gets down to Mannheim-Kazanas solution.

So, Weyl-Dirac gravitation can be used as an alternative theory to explain the dark matter phenomenon. We should note that the required deviation of Dirac function /(t) from unit is small (when measured in Planck units of mass).

Conclusion

The paper discusses the models of conformal gravitation with Lagrangians linear in scalar curvature and minimal coupling with the scalar field. A variant of the conformal Lagrangian with two scalar fields is proposed, in which the Weyl vector is replaced by a vector that gets transformed like the Weyl vector, but is not a part of the Weyl connection. The space of such a model is the integrable Weyl space.

Within the Weyl’s theory of gravitation with a non-minimal coupling of a real scalar field, the problem of describing the conformal stage of the evolution of the Universe, based on the Friedmann metric, is considered. Conformal-invariant solutions for the scale factor are presented and it is shown that quantum corrections to the trace of the energy-momentum tensor violate conformity, partially they are compensated by the gauging of the Dirac function that leads to the Lagrangian of the general theory of relativity.