Operations and Ranking Methods for Intuitionistic Fuzzy Numbers, a Review and New Methods
Автор: Abazar Keikha, Hassan Mishmast Nehi
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 1 vol.8, 2016 года.
Бесплатный доступ
Intuitionistic Fuzzy Numbers (IFNs) transfer more information than fuzzy numbers do in uncertain situations. It is caused that many others tried to define methods for ranking of IFNs and arithmetic operations on them, which are used in practical applications of IFNs such as decision making. Arithmetic operators on IFNs changed membership and non-membership degrees. The resulted degrees have important interpretations in real application of IFNs. In this paper, we will first review the existing methods for ranking and arithmetic operations on several representations of IFNs. Then, we will propose a new method based on arithmetic mean and geometric mean to compute membership and non-membership degrees of resulted IFN from arithmetic operations on IFNs. It is caused that the resulted degrees don't change monotonousness and be closer to reality. Furthermore, a new method for ranking of IFNs will be proposed. Finally, the proposed methods are used in the numerical examples, compared to some other existing methods.
Fuzzy Numbers, Intuitionistic Fuzzy Numbers, Ranking of IFNs, TrIFN
Короткий адрес: https://sciup.org/15010785
IDR: 15010785
Текст научной статьи Operations and Ranking Methods for Intuitionistic Fuzzy Numbers, a Review and New Methods
Published Online January 2016 in MECS
-
I. Introduction
After the introduction of the Theory of Fuzzy Sets (FSs) by Zadeh in 1965 [45]; Atanassov generalized Zadeh’s Fuzzy Sets in 1983, it is called Theory of Intuitionistic Fuzzy Sets (IFSs) [1]. These concepts enabled scientists to model vague and uncertain situations, occurred in many practical problems. However, because of more information which is carried out by the IFSs than FSs, recently, many authors have been interested to apply them in different contexts. IFSs are based on membership and non-membership degrees, but, in many real problems, these values are difficult to be expressed as crisp numbers. Instead, the range of them can be specified. In this case the concept of IFS generalized to Interval-Valued Intuitionistic Fuzzy Set (IVIFS) by Atanassov and Gargov [4]. More details on IFSs have been presented in [1-7].
Vague Sets, another concept for the analysis of vague/uncertain situations, proposed in 1992 by Gau and Buchrer [14]. Bustince and Burillo [10] showed that vague sets are IFSs. Xu [38] used this homology and developed some intuitionistic fuzzy aggregation operators for aggregating intuitionistic fuzzy information and established various properties of these operators. In [37], there exist more details on aggregation of IFS and IVIFS information which, were presented by Xu and Cai. Liu and Yuan [20] introduced another type of IFS called triangular IFS (TIFS) where, membership and nonmembership degrees are triangular fuzzy numbers in [0, 1]. Beg and Rashid [9] introduced the concept of Trapezoidal-valued Intuitionistic Fuzzy Set (TrIFS), where membership and non-membership degrees are trapezoidal fuzzy numbers in [0, 1].
Qiang and Zhong [27, 28] proposed another type of Trapezoidal Intuitionistic Fuzzy Numbers (TrIFNs), are defined with real parameters, membership and nonmembership degrees. They proposed some aggregation operators on TrIFNs and apply them in solving multi criteria decision making problems. Parvathi and Malathi [25] defined arithmetic operations on symmetric TrIFNs.
Solving of Multi Attribute Decision Making (MADM) problems is one of the most practical applications of IFNs that, apply the defined arithmetic operations on IFNs or their ranking methods [8, 9, 11-13, 15-18, 21-23, 26-36, 40, 42, 46]. For example, Sagaya and Henry [29], proposed a new method for ranking intuitionistic fuzzy numbers based on the circumcenter of centroids of membership function and nonmembership function of intuitionistic fuzzy numbers. To compute the circumcenter of a trapezoidal intuitionistic fuzzy number, first the trapezoids of membership function and nonmembership function are divided into three regions, a triangle, a rectangle and a triangle respectively. Then the centroids of three figures of membership function and nonmembership function are calculated followed by the calculation of the circumcenter of these centroids. Finally ranking functions of membership function and nonmembership function of intuitionistic fuzzy number are defined which, are the Euclidean distances between the circumceter point and the original point respectively to rank intuitionistic fuzzy numbers. In this paper, because of the importance of membership and nonmembership degrees of IFNs, we proposed a new method to determine them with respect to the obtained IFN from arithmetic operations, also, a new method for ranking of IFNs is proposed.
The rest of the article is organized as follows: In Section two, needful preliminaries, such as fuzzy sets and fuzzy numbers, IFSs and IFNs, arithmetic operations on IFNs and some existing method for ranking of IFNs are presented. We proposed a new method for arithmetic operations on IFNs which is caused to membership and non-membership degrees obtained in a real manner in Section three. A new method for ranking of IFNs is proposed in Section four. Numerical examples are given in Section five. Conclusions and recommendations are presented in Section six.
-
II. Definitions and Preliminaries
In this section, some basic concepts and definitions are introduced, which will be used in the sequent sections. Some real problems have uncertain or vague information. In these cases, Fuzzy Sets Theory, which has been introduced by Zadeh [45] in 1965, is very helpful. Atanassov [6] generalized FSs to IFSs, which carry out more information about uncertain situations.
Definition 2.1
Let X is the universal set:
0 A set A = { ( x , m.. ( x ) ) | x е X } is called a fuzzy set of X where, m- ( x ) : X ^ [ 0,1 ] is membership function that, for all x е X; m^ ( x ) expresses the degree of membership of element x in A .
-
ii) A set A = { ( x , m . ( x ) , n . ( x ) ) | x е X } is called IFS of X where, m ( x ), n ( x ) are membership function and non-membership function, respectively, so that: 0 < m ^ ( x ) + n ^ ( x ) < 1, V x е X .
For each IFS in X, n (x) = 1 - m^ (x) - n^ (x) for all x е X is called intuitionistic fuzzy index or hesitation degree of x in A . It is obvious that 0 < n~ (x) < 1. Fig. 1 shows geometrical interpretation of IFS and FS [31]. We can imagine a unit cube with three edges given by these parameters, as (m, n, п) е [0,1]3 . Because of the condition m + n + тс = 1, the values of the parameters characterizing an intuitionistic fuzzy set can belong to the triangle ABD only. Each x е X is mapped on ". in the triangle ABD. If тс = 0, we have m + n = 1 that, in Fig. 1 this condition fulfilled in segment AB . Then AB viewed to represent a described FS by two parameters; m, n. The triangle ABC is orthogonal projection of the triangle ABD gives a representation of an intuitionistic fuzzy set on the plane where, the interior of triangle ABC is the area with n > 0. The orthogonal projection of segment AB on the axis m (in [0,1] ) gives a fuzzy set represented by only one parameter .
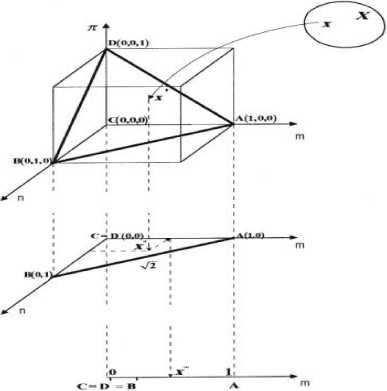
Fig.1. Geometrical Interpretation of IFSs and FS
Definition 2.2
-
[3] Suppose that A and B be two IFSs with membership functions m ( x ) and m ( x ) , nonmembership functions n ( x ) and n ( x ) respectively, then:
-
2)
-
3)
-
4)
-
5)
-
6)
-
7)
-
8)
-
9)
-
A c B о V x е X : m -( x ) < m6 ( x ) & n- ( x ) > ns ( x );
A = B о V x е X : m ( x ) = mb ( x ) & nA ( x ) = n6 ( x );
A = { ( x , n A ( x ), m A ( x ) ) | x е X } ;
A u B = {(x, min( mA (x), m& (x)), max (nA (x), n§ (x)) | x е X};
A u B = {( x ,max ( mA ( x ), m6 ( x ) ) ), min ( nA ( x ), n ^ ( x ) ) | x е X };
A + B = {( x , mA ( x ) + m6 ( x ) - mA ( x ). m6 ( x ),
n A ( x )n B ( x )) I x е X } ;
-
A . B = {( x , m A ( x )^m6 ( x ), n A ( x ) + n B ( x ) - n A ( x ) nB ( x ))| x е X } ;
A A = {( x ,1 - (1 - m A ( x)) л ,( n A ( x )) л )|
AA = {(x,(mA (x))A ,1 - (1 - nA (x))A )| x е X}, A > 0.
An IFS such as A on universal set x is called intuitionistic normal if there exist x0 e X and xt e X such that m ~ ( x 0) = 1 and n^ ( x ) = 1.
In the above definition, membership and nonmembership values are crisp but, in many real problems it is impossible to determine them exactly. Atanassov and Gargov [4] introduced the IVIFS, when the range of membership and non-membership degrees can be determined.
Definition 2.3
-
[4] An IVIFS A over X is defined as an object of the form A = {( x , m ~ ( x ), n^ ( x )) | x e X } where, m A ( x ) = [ m A ( x ) l , m A ( x ) u ] C [0,1] and n A ( x ) = [ n A ( x ) l , n A ( x ) " ] c [0,1] are intervals, and for all x e X : т-д ( x ) " + n A ( x ) " < 1.
Let A = { < x ,[ a , a " ],[ bl , b " ] > | x e X } and B = {< x ,[ c , c " ],[ d , d u ]> | x e X } be two IVIFSs which are defined on universal , then ([4, 38]):
-
2)
-
3)
-
4)
A' = { < x ,[ b l , b " ],[ a l , a " ] > | x e X };
A n B = { < x ,[min{ al , cl },min{ a " , c " }],[max
{ bl , dl },max{ b " , d u }] > | x e X };
A и B = {^ x ,[max{ al , cl },max{ a " , c u }],[min{ bl , d1 },min{ bu , d" }]^| x e X } A + B = { < x ,[ al + cl - al .c , a " + c u - a " . c " ],
[ bl . dl , b " . d " ] > | x e X };
XA = { < x ,[1 - (1 - al ) X ,1 - (1 - a " ) л ],
( bl ) X ,( b " ) X > | x e X }, X > 0;
A X = { < x ,[( al ) X ,( a " ) X ],[1 - (1 - bl ) X ,
-
1 - (1 - b " ) X ] > | x e X }, X > 0.
Finally, normal and convex IFS on with upper semi-continuous membership function and lower semi-continuous non-membership function called Intuitionistic Fuzzy Number (IFN).
There are two types of IFNs. The first type contains the IFNs that are expressed, only, by the membership and non-membership degrees are interpreted as satisfaction and non-satisfaction degrees, respectively. These quantities may are crisp or uncertain, which will be discussed in detail. The latter, in addition to membership and non-membership degrees, are interpreted as the maximum of satisfaction and the minimum of nonsatisfaction degrees respectively, including fuzzy numbers.
-
A. The first type representation of IFNs
Based on Vague Sets concept [14], which are characterized by a truth-membership function and a false-membership function and its similarity to IFS, have been shown by Bustince and Burillo [10], Xu [38] defined as an IFN or an intuitionistic fuzzy value (IFV), where and such that
It is obvious that in this form, (1,0) is the largest IFN and (0,1) is the smallest one. Voting can be a good example of such a situation as the human voters may be divided into three groups: vote for, vote against and abstain or giving invalid votes [31]. For instance let the physical interpretation of such numbers can be expressed as " the vote for the resolution is 6 in favor, 1 against and 3 abstentions" [37].
Definition 2.4
-
[37] Let A = ( m~A , nA ) and B = ( m ^, n ^) be IFNs. Then:
-
1) A' = ( n A , m A );
-
2) A n B = (min{ m ^, m B },max{ n -, n B });
-
3) A и B = (max{ m -, m -},min{ n -, n -});
-
4) A + B = ( m A + m B - m A .m B , n A .n B ); (3)
-
5) A . B = ( m A .m B , n A + n B - n A .n B );
-
6) XA = (1 - (1 - m A ) X , n A X ), X > 0/
-
7) A X = ( m A X ,1 - (1 - n A ) X ), X > 0.
Intuitionistic fuzzy aggregation operators are developed by Xu, see [37], he also, introduced IntervalValued IFNs (IVIFNs) and developed aggregation operators on them [41].
Definition 2.5
-
[41] an ordered pair such as A = ([ a , b ],[ c , d ]) where, [ a , b ] and [ c , d ] are subinterval in [0,1] such that b + d < 1, is called an IVIFN. In this form, ([1,1],[0,0])is the largest IVIFN and ([0,0],[1,1]) is the smallest one.
Some defined operational laws of IVIFNs are introduced as follows:
Let A = ([ al , a " ],[ bl , b " ]) and B = ([ cl , c " ],[ dl , d " ]) be two IVIFNs, then ([34, 41]):
A '= ([ bl , b " ],[ al , a " ]);
A n B = ([min{ al , cl },min{ a " , c " }], [max{ bl , dl }, max{ bu , du }]);
A ∪ B = ([max{ al , cl },max{ au , cu }], [min{ bl , dl }, min{ bu , du }]);
λA = ([1 - (1 - al ) λ ,1 - (1 - au ) λ ],
[( bl ) λ ,( bu ) λ ]), λ > 0;
A λ = ([( al ) λ ,( au ) λ ],[1 - (1 - bl ) λ , 1 - (1 - bu ) λ ]), λ > 0.
Liu and Yuan [20] displayed the membership and nonmembership degrees of an IFN by triangular fuzzy numbers in [0,1] and introduced Triangular IFNs (TIFNs). Also, similarly to Liu's work, Beg and Rashid [9] and Ye [42] defined the trapezoidal IFNs (TrIFNs).
Definition 2.6
-
[20] A triangular intuitionistic fuzzy number that, its membership and non-membership degrees are triangular fuzzy numbers in [0, 1], displayed by
〈 [ al , a , au ],[ bl , b , bu ] 〉 where, al , a , au , bl , b , bu ∈ [0,1], and a u + b u ≤ 1.
Also, Liu and Yuan [20] presented some operations of two TIFNs.
Let A =< [ a 1 l , a 1 , a 1 u ],[ b 1 l , b 1 , b 1 u ]> and
B =<[ a 2 l , a 2 , a 2 u ],[ b 2 l , b 2 , b 2 u ]) be two TIFNs. Then [20]:
λ A =〈 [1 - (1 - al ) λ ,1 - (1 - a ) λ ,1 - (1 - au ) λ ], [( b 1 l ) λ ,( b 1 ) λ ,( b 2 u ) λ ] 〉 , λ > 0;
A λ =〈 [( a 1 l ) λ ,( a 1 ) λ ,( a 1 u ) λ ],[1 - (1 - b 1 l ) λ ,1 - (1 - b 1 ) λ ,1 - (1 - b 2 u ) λ ] 〉 , λ > 0.
Definition 2.7
-
[42] A TrIFN which, its membership and nonmembership degrees are trapezoidal fuzzy numbers in [0,1] displayed by
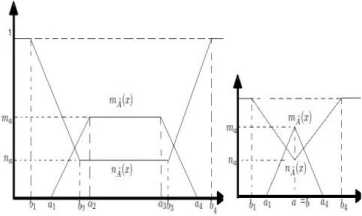
Fig.2. General TrIFN & TIFN
A = 〈 [ a 1, a 2, a 3, a 4],[ b 1, b 2, b 3, b 4] 〉 where, a , a , a , a , b , b , b , b ∈ [0,1] and a + b ≤1.
Some defined operational laws for two TrIFNs are as follows [9, 42]:
Let A = 〈 [ a 11 , a 12 , a 13 , a 14 ],[ b 11 , b 12 , b 13 , b 14 ] 〉 and B = 〈 [ a 21, a 22, a 23, a 24],[ b 21, b 22, b 23, b 24] 〉 be two TrIFNs. Then:
A + B =〈 [ a + a - a a , a + a - a a ,
a 13 + a 23 - a 13 a 23 , a 14 + a 24 - a 14 a 24 ],
[ b 11. b 21, b 12. b 22, b 13. b 23, b 14. b 24] 〉 ;
A . B =〈 [ a 11 a 21 , a 12 a 22 , a 13 a 23 , a 14 a 24 ],
2) [ b 11 + b 21 - b 11 b 21 , b 12 + b 22 - b 12 b 22 , (6)
-
b 13 + b 23 - b 13 b 23, b 14 + b 24 - b 14 b 24] 〉 ;
λ A =〈 [1 - (1 - a 11 ) λ ,1 - (1 - a 12 ) λ ,1 - (1 - a 13 ) λ , 1 - (1 - a 14 ) λ ],[ b 11 λ , b 12 λ , b 13 λ , b 14 λ ] 〉 , λ > 0;
A λ =〈 [ a 11 λ , a 12 λ , a 13 λ , a 14 λ ],[1 - (1 - b 11 ) λ ,
-
4) 1 - (1 - b 12 ) λ ,1 - (1 - b 13 ) λ ,
1 - (1 - b 14 ) λ ] 〉 , λ ? > 0.
-
B. The second type representation of IFNs
Qiang and Zhong defined another type of IFNs [27]. In this type, IFNs are defined based on membership and non-membership functions, where, right basis function of membership function and left basis function of nonmembership function are continuous monotone decreasing functions, left basis functions of membership function and right basis functions of non-membership function are continuous monotone increasing functions.
In the following, TIFNs, TrIFNs and some defined arithmetic operations on them are reviewed. Fig. 2 shows a general TrIFN and TIFN.
Note: If for an IFN, a = b ; i = 1,2,3,4, it is called canonical IFN.
Definition 2.8
[20] A TIFN such as л represented by
A = < ( b , ax , a = b,a 4, b 4); ma , na > where bi < ai < b = a < a 4 4 < b4 ; is a special case of IFN with membership function m and non-membership function n which are defined as:
0; x < ax or x > a4, m, = <
A
x - a
-----1 ma; ax < x < a, a - ax ma;x = a, a4 - x
—4---- mn ; a < x < a, , a 4
-
a 4 - a
'1; x < b i or x > b 4 , b - x + nn(x - b)
b 4 " a ; M x < b ,
"a ; x = b, x " b + "a (b4 " xI „, ; b < x < b
I b 4 - b a 4
Definition 2.9
-
[20] A TrIFN such as represented by
A = < ( b i, ai,b 2, a 2 , a 3, b 3, a 4, b 4); ma , na > where bx< a , < b 2< a 2< a 3< b 3< a 4< b 4; is a special case of IFN with membership function m and nonmembership function n which are defined as:
the latest one is presented by Wang et al. [34] in 2013.
Definition 2.10
-
[27] Suppose A = < ( au,a u, a i3 , a i4 ; m a ),( b n, b 2 ,^3, b i4 ; " a ) > and B = < ( a 2p a 22, a 23, a 24; mb ),( bpb 2, b 3, b 4; nb ) > to be two TrIFNs, then:
A + B = < ( a n + a 2 p a 12 + a 22, a 13 + a 23, a 14 +
-
i) a 24 ; m a + m b - m a .mb ),( b n +
b2i, bi2 + b22, bi3 + b23, bi4 + b24; "a • nb )>;
A - B = < ( axx - a 24, a 12 - a 23, a 13 - a 22, a 14 -
-
2) a 2i ; m a + m b - m a . m b ), ( b ii - (7)
b 24 , b i2 - b 23 , b i3 - b 22 , b i4 - b 2i ; n a . n b ) > ;
< ( a ii . a 2i , a i2 . a 22 , a i3 . a 2 3 , a i4 - a 2 4 ; m a . m b ), ( b ii .b 2i , b i2 . b 22 , b i3 . b 23 , b i4 . b 24 ; " a +
" b - " a . " b ) > , A > 0, B < °;
A . B = j
,
0; x < ax or x > a4, m~ = < A
x - a
------- ma; ax < x < a2, a2 - ax ma; a2 < x < a3,
-
a - x . .
-------m a ; a 3 < x < a 4 , a, - a
-
< ( a i4 . a 24 , a i3 - a 23 , a i2 * a 22 , a ii a 2i ; m a • m b ), ( b i4 . b 2i , b i3 . b 22 , b i2 . b 23 , biVb 24 ; " a + ^ nb - na . nb ) > , A < 0, B < 0;
2 A = < ( X ax ,, X ax T , 2 a , 3, 2 a , 4 ;i - (i - mQ ) x ), ( 2 b n, 2 b i2 , 2 b i3 , 2 b i4 ; na2 ) > ; 2 > 0.
" a =i
b 2 - x + " a ( x - b i )
b 2 - b 1
a ;1
2 ,
x - b 3 + na ( b 4 - x )
b 4 - b
a ; 3
In this paper, a TrIFN is displayed by A = < ( a i, a 2, a 3, a 4; ma),(bi,b2,b 3, b4;na ) > and
A = < ( a , a , a 4; mQ ),( b , b , b 4; no ) > displayed a TIFN. The arithmetic operations of this type of IFNs are defined similarly to the arithmetic operations of fuzzy numbers. As we will see, to compute membership and nonmembership degrees of resulted IFN from arithmetic operations, there exist three methods. The first method is presented by Qiang and Zhong [27] in 2009, the second, introduced by Nan et al. [21] and Li [18] in 2010, also,
If A and B be two TIFNs, it is sufficient to replace in the above formulas a ,2 = a ,3 = a , and b ,2 = b ,3 = b ,.
The following definition shows how to compute membership and non-membership degrees of resulted IFNs from arithmetic operations (the second method):
Definition 2.11
[i8, 2i] Let A = < ( a n, a i , a i4 ; m a ),( b n, b i , b i4 ; " a ) > and B = < ( a 2p a 2, a 24; mb ),( b2pb 2, b 4; nb ) > to be two TIFNs, then:
A + B = < ( a n + a 2 p a + a 2, a 14 + a 24;min{ ma , mb }), ( b p + b 2i , b i + b 2 , b i4 + b 24 ; max { " a , " b } > ;
A - B = < ( a ii - a 24, a i - a 3, a i4 - a 2i;min{ m a , m b }), ( b ii - b 24 , b i2 - b 23 , b i3 - b 22 , b i4 - b 2i ; " a . " b ) > ;
(( a11.a 21 , a 12 . a 22 , a 13 .a 23 , a 14 . a 24 ; max{ ma , mb }),( b 11 . b 21 , b 12 . b 22 , b 13 . b 23 , b 14 . b 24 ;
min{ na , n 4})), A > 0, B < 0;
(( an .a 24 , a i2 . a 23 , a i3 .a 22 , a M a 21 ; max{ ma , A . B = ^ m b }), ( b n . b 24 , b i2 . b 23 , b i3 . b 22 , b i4 . b 2i ;
min{ П а , П ь })), A > 0, B < 0;
(( a 14 . a 24 , a 13 . a 23 , a 12 . a 22 , a 11 . a 21 ; max{ m a , m b }),( b 14 . b 21 , b 13 . b 22 , b 12 . b 23 , Ь 11 . Ь 24 ;
min{ na , n 4}) ) , A < 0, B < 0;
( ( X a1 1 , X a12, X a13, X a14 ;1 - (1 - ma ) X ),
|
( X b 11 , X b 12 , X b 13 , X b 14 ; n a X », X > 0; |
||
|
4) |
X A = ^ |
|
X A = ((X a 1 1 , X a 12 , X a 13 , X a 14 ;1 - (1 - ma )Л ), (X b 11 ,X b 12 ,X b 13 ,X b 14 ;naX ) ) ; X > 0.
Wang et al. [34], firstly, expressed the weaknesses of the previous approaches in determining of membership and non-membership degrees in arithmetic operations, then, they proposed a new method to compute them.
Definition 2.12
-
[34] Let A = ( ( a n, a 1 , a 1 4; m a ),( b n, b 1 , b 14 ; n a ) } and B = ( ( a 21 , a 2 , a 24 ; m b ), ( b 21 , b^ , b 2 4 ; П ь ) ) be TIFNs, let
I a 11| + 2 | a 1| + | a 141 ||^ГЦ _ | b | + 2 | b 1| + | b u|
I a 21| + 2 | a 2 | + | a 241 ||y ,|| _ | b 21| + 2 | b 21 + | b 241
( ( X a M, X a B, X a ^, X a n;1 - (1 - m a ) X ), ( X b 14 , X b B, 2 b 12 , X b n; na X ) ) , X < 0;
then:
- - ||A\ ma + | B|
A + B = (( a ^ + a 2 j, a^ + a 2, a 14 + a 24;—■—:
If A and B be two TrIFNs, the above definition can be generalized to obtain operational laws of TrIFNs:
Suppose A = (( an,a ^, a ^, a ^; m a ), ( b u, Ь 12, b B, b 14; n a )) and B ( ( a 21 , a 22 , a 23 , a 24 ; m b ),( b 21 , b 22 , b 23 , b 24 ; n b ) ^ to be two TrIFNs, then:
( Ьц + b 21 , Ь 1 + b 2, Ь 14 + Ь 2 4 ;
A - B = ( ( a 11 -
a 21, a 1 - a 2, a 14 - a 24;
m
b ),
n a + I B'| П Ь
mb
A + B = ( ( au + a 2 p a 12 + a 22, a 13 + a 23, a 14 +
-
1) a 24 ;min{ m a , m b }),( b p + b 21 ,
b 12 + b 22 , b 13 + b 23 , b 14 + b 24 ;
max{ n a , n b }) ) ;
A - B = (( a 11 - a 24 , a 12 - a 23 , a 13 - a 22 , a 14 -
-
2) a .м] m a , m b }),( b 11 - b 24 ,
-
b 12 - b 23 , b 13 - b 22 , b 14 - b 21 ; max{ n a , П ь }));
-
( ( a11 .a 21 , a 12 . a 22 , a 13. a 23 , a 14. a 24 ;
max{ m a , m b }),( Ь 11 Ь 21 , b 12 . b 22 , b 13 Ь 23 , b 14 Ь 24 ;
min{ n a , n b }», A > 0, B < 0;
( Ь 11 - Ь 24 , Ь 1 - Ь 2 , Ь 14 - Ь 2
|| Ama + | B| 21 ;
m
—».
Ranking of IFNs, is necessary in some practical application of IFNs, is discussed by many authors [13, 15, 17, 18, 22, 26, 27, 29, 36, 46]. In the rest of this section, some of the existing ranking methods will be reviewed.
Li [17, 18] proposed to use value and ambiguity indices. Let A = ( ( ax , a , a 4; ma ),( b , b , b 4; na ) ) be a TIFN, then
V ( A, X ) = V ц ( A ) + X (V v ( A ) - V ц ( A )),
A ( A , X ) = A ^ ( A) + X ( A v ( A ) - A ^ ( A )), Л e [ 0,1 ] ,
( ( a 11. a 24, a 12. a 23, a 13. a 22, a 14. a 21;
max{ ma , mb }),( b 11. b 24, b 12. b 23, b 13. b 22, b 14. b 21;
min{ na , nb }) ) , A > 0, B < 0;
are value and ambiguity indices respectively where, maL(a) + R(a) z x
V. (A )=! ( )9 ) f (a) da,
Vv(A, = j£(£).«(£) f(e)dв, na
( ( a 14 . a 24 , a 13 . a 23 , a 12 . a 22 , a 11 . a 21 ;
max{ m a , m b }),( b 14 .b 21 , b 13 . b 22 , b 12 . b 23 , b 11 .b 24 ;
mm! n a , n b }) ) , A < 0, B < 0;
f (a) on [0, ma ] is nonnegative and non-decreasing ma function, satisfied in f (0) = 0 and J f (a)da = m . Also, 0
nonnegative and non-increasing function g(p) with 1
conditions J g ( Д ) d p = 1 — n , g (1) = 0 is defined on [ n a ,1]. n a
Now, if A = ( ( a 1 , a , a 4 ); ma , na ) and B = { ( b 1 , b , b 4); m b , n b ) be two arbitrary TIFNs, based on proposed method in [17], the TIFN which, its value index is greater will be better, else, if their value indices are equal, the greater one, has a small ambiguity index. If both value indices and ambiguity indices of these TIFNS are equal, then they are equal.
Also, based on ambiguity and value indices, Li [18], proposed to obtain
Peng and Chen [26], in order to rank the canonical IFNs, proposed a new method based on the concepts of center index and radius index of canonical intuitionistic fuzzy numbers. According to this method, let A = [a.,b,c.,d;m,n],i = 1,2,.,n, be arbitrary canonical intuitionistic fuzzy numbers. Then with respect to each number, first calculate center index ai +2bi+2ci +di (mi+ ni-1)2 mCIF(Ai) = r [ o +
(1 - n,-)2 + (1 - nt)(mi + ni -1)], and radius index
R ( A, 2) = V ( A , 2
1 + A ( A, 2)
and
™„ ( A i ) = ~“■ " 2b' + 2 c- + d ' V
(1 - n ) 2 + (1 - n )( m i + n i - 1)].
R ( B , 2 ) =
V ( B , 2 )
1 + A ( B , 2 )
Then, compute ranking index
then the bigger one has greater ratio.
Qiang and Zhong [27] proposed accuracy function and score function with respect to TrIFN
5 ( A ) = I ( A ) x ( ma — na ) is its score function,
H ( A ) = I ( A ) x ( ma + na ) is its accuracy function and
I ( A ) =
( ax + a 2 + a 3 + a 4) x (1 + ma - na )
is mean value of TrIFN A . Then the number which, its score function is greater, has greater rank, otherwise, the greatest number has a greater accuracy function. If, both accuracy function and score function of two TrIFNs are equal, then, they are equal.
Nayagam et al. [22] proposed a new method for ranking of interval-valued intuitionistic fuzzy sets. Let A = ([a,b],[c,d]) , be an interval-valued intuitionistic fuzzy number, a general accuracy function LG of an interval-valued intuitionistic fuzzy value, based on the unknown degree is defined as
( a + b )(1 - 5 ) + 5 (2 - c - d )
LG ( A ) =-----------------------,
2 (12)
where, 5 e[0,1] is a parameter depending on the individual intention. If A = { [ ax , b ],[ cx , dx ] } and A =( [ a 2, b 2],[ c 2, d ] ) be two IVIFSs. For some values of 5 we have LG ( A ) > LG ( A ), then A > A , and for some other values of 5 we have LG ( A ) < LG ( A ) , then A < A .
r ( A i ) = m CIF ( A i ) +
1 + am,, ( A i )
where, 0 reflects the degree of optimism of a decision maker. A larger value of indicates a higher degree of optimism. Finally, the ranking of the n canonical intuitionistic fuzzy numbers are according to nonincreasing order of r ( A ), i = 1,2,..., n .
Sagaya [29] based on the circumcenter of centroids of membership function and non-membership function of intuitionistic fuzzy numbers proposed a ranking method for TrIFNs. In this method, one obtain circumcenters of centroids of membership function and non-membership function of TrIFN A = ( ( ax , a 2, a 3, a 4; ma ),( b , b 2, b 3, b 4; na ) ) as ( x 0, y 0) and ( x ' , y ' ) respectively. Then, r ( A ^ ) = 4X o 2 + y 02 and r ( A v ) = 4X o2 + y 02 are used in comparison process:
Let A and B be TrIFNs then A > B if we have r ( A p ) > r ( B p ) or r ( A ^ ) = r ( B p ) & - r ( A v ) >- r ( B v ). If r ( A ^ ) = r ( B M ) and r ( A ) = r ( Bv ), then A = B .
Recently, De and Das [13], similarly to Li's method, proposed another method to compare TrIFNs. For each TrIFN A = ((ax, a, a4 ); ma, na ) they obtain the value and ambiguity indices based on Li's method as i V (A)+vu (A) - i av (A)+au (A)
-
V ( A ,-) = vl±YL , A ( A ,^) = 2 Ц
and compute r(A) = у(A,l) + a(A,1). Based on this method, the greater TrIFN has greater R(A).
Wang et al. [35] presented the correct centroid formula for fuzzy numbers and justify them from the viewpoint of analytical geometry:
Definition 2.13
Suppose A — ( a , a 2, a 3, a 4; m ) to be a TrFN. They computed the coordinates the center of gravity of the as:
— ax a2
х^ — — [ ax + a^. + а з + a^
—
a 3 a 4 a 1 a 2
( a 3 + a 4) — ( ax + a 2)
— m a — a y0 — [1 +---------3----2-------].
0 3L ( a 3 + a 4 ) — ( a 1 + a 2 )'
Finally, the rank of fuzzy number determined by:
We will extend the above definition for IFNs and apply it for ranking of IFNs.
-
III. New Methods for Arithmetic Operations on Ifns and RANKING of THEM
In this section we proposed new methods for arithmetic operation on IFNs and ranking of them.
-
A. A new method for arithmetic operation on IFNs
It is believed that the IFNs carry out more information than the FNs. It is because of non-membership degree which is used in IFNs simultaneously with membership degree. Membership and non-membership degrees play basic roles in the analysis of resulting information from data processing. Therefore, obtaining right degrees are important issues in arithmetic operation processes. As we see before, there are many methods to compute these degrees. In some methods min and max operators [19] are used to determine these parameters and the other one used mathematical formulas to compute them [7, 27, 34]. But, using and operators caused to the other degrees don't participate in computing final degrees. In the proposed methods in [7, 27], let A, i — 1,2,..., n, be IFNs which their membership and non-membership degrees displayed by m, n, then nn mA = 1 — П(1 — mA ), nA = nnA , i—1 i—1
are membership and non-membership degrees of
n
XAi i—1
and nn mA —Пт, nA — 1 — П(1 — nA), i—1 i—1
n
are membership and non-membership degrees of П A ,?
i — 1
respectively. In this method, because of
0 < m~., n ~ < 1 then AiAi nn mA — 1 —П(1 — mA) ^ 1,nA —nnA ^ 0,
— 1 i — 1
while n increased, and it is a problem. For this reason, we use arithmetic and geometric mean operators to obtain membership and non-membership degrees of resulted IFNs from the arithmetic operations process on the IFNs which are introduced by Wang [27]. Based on our proposed method, the arithmetic operations on TrIFNs and TIFNs can be defined as follows:
Definition 3.1
Let A — ( ( an, a. 12 , « 13 , ^4 ; m a ),( b n, b n, ^, b M; na ) ) and B — { ( a 2p a 22, a 23, a 24; mb ),( b2p b 22, b 23, b 24; nb ) ) to be two TrIFNs, then:
A + B — \(ax ^ + a2 j, a12 + a22, a13 + a23, a14 +
-
1) a 24 ; m a + m b ), ( b n + b 21 , b 12 + ?
b 22 , b 13 + b 23 , b 14 + b 24 ; V nO^n T ) > ;
A—B — ((au — a24, an — a23, a^ — a22, a14 — m„ + m
-
2) a 21 ; 2 ),( b 11 b 24 , b 12
b 23 , b 13 — b 22 , b 14 — b 2 ; V n a^ n ? )>; (
( ( a11 .a 21 , a | 2 .a 22 , a13 .a 23 , a | 4 . a 24 ;
^т ^ .^ ),( b n^, b12 .b 22 , b 13 b 23 , b14 .b 24 ; n a l n b ) ) , A > 0, B < 0;
( ( a 11 . a 24 , a 1 2 . a 23 , a 1 3 . a 22 , a 14 .a 21 ;
A . B — j
n a + n b
\ ( a 14 . a 24 , a 13 . a 23 , a 12 . a 22 , a n . a 21 ;
л(тЛ ь ),( b 14 b 21 , b 13 b 22 , b 12 b 23 , b11b 24 ; n^ + n^)\
A < 0, B < 0;
|
'( ( A an, A a j2 , A a 13, A a 14 ; ma ), ( A b u, A b 12 , A b 1 3, A b 14 ; na ) ) , X > 0; |
|
|
4) A A = J |
( ( A a 14 , Xa13, A a j2 , A a „; m0 ), _ (Ab14,Xbu,Ab„bb;nna ) ) , A < 0; |
0 < mmi + ^n . < Xt ^
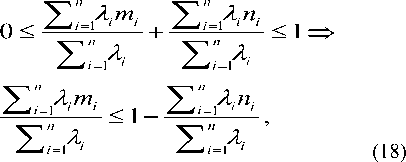
The above definition, in a similar way, can also be updated to canonical TrIFNs. For any numbers of canonical TrIFNs, the definition 3.1 is extended as follows:
Definition 3.2
Let A = [ a. , b , c. , dt ; mt , n ], i = 1,2, ™ , n ; be canonical TrIFNs, be positive canonical TrIFNs, then
in the other hand, we know that geometric averaging of numbers is less than their arithmetic averaging, hence:
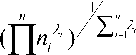
Zn An i=1 i i i=1
Z n An ^^ i = 1 i 1
Zn A i=1 i
n nnnn
A = Z A = &, Z b , Z c, Z d ; m, n ]
г = 1 i = 1 i = 1 i = 1 i = 1 (16)
and n nnnn
A = n^ = № Л ПЛ № W’ m , n 1 = 1 i = 1 i = 1 i = 1 i = 1
are TrIFNs, where
Уn A i = 1 i
n n
< 1 - (П " - 1 )7 Z^ A i
i = 1
and then from Eq. 18 and Eq. 19, we have:
n>Ln ^i
^Z^ i = 1 i 1
nAn A i =1 i
thus,
,?
n 1 n
- (ПпЛу zi-л, i =1
m =
nm
Z—t i = 1 i
, n =
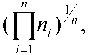
n m '= ( П m i ) i = 1
1 n
Z n n , n' = ^ i =1
Z n mnt
Д^ i =1 1 i
Z n A i =1 i
n n
+(П"»"1/Z “ i=1
The following theorem shows that the obtained membership and non-membership degrees are satisfied in intuitionistic fuzzy condition.
Theorem 3.1
Let A = [ai,bi,ci,di;mi,ni],i = 1,2,...,n ; be canonical TrIFNs, then membership and non-membership nn degrees of A = Zaa and A =ПAA are satisfied in i=1 i=1
IFN's condition, where A > 0, i = 1,2,..., n ; i.e.:
Proof
We prove only for A = Z XtA . Based on the definition i = 1
of IFNs, for all 1 < i < n : 0 < mt + n < 1 and we have:
B. A new method for ranking of IFNs
In this subsection we proposed a new method based on centroid points, to rank IFNs.
In the Sagaya's method [29], let A and B be TrIFNs where and are centroid points of their membership functions, respectively. Let and be the centroid points with respect to their non-membership functions, respectively. Then, this method expressed incorrect result A = B .
In our proposed method, Wang's method is used to obtain the centroid points of membership function and non-membership function. If we assume that A = ( ( a , , a 2, a 3, a 4; ma ),( b 1 , b 2, b 3, b 4; na ) ) be a TrIFN, we extend the Wang's method to determine circumcenter points of membership and non-membership functions. As we know in definition of TrIFN, membership and nonmembership functions are trapezoids. According to the Wang's method, the centroid point of membership function is obtained i.e.
x0 m = “[ al + a 2 + a3 + a 4 - a3a4 1 2
( a3 + a 4 ) - ( a 1 + a 2 ) ,
mri a - a
У 0 m = T[1 + / ^ 4 / ^J -
3 ( a 3 + a 4) - ( a , + a 2)
- aa
Now, based on the W a ng 's method, we calculate the circumcenter point ( x ' , y ' ) of determined trapezoid by ( b , b^ , b , b 4 ;1 - n ). Then, the circumcenter point of the determined trapezoid by ( b , b , b , b ; n ) is obtained as:
( x 0 n , У 0 n ) = ( x 0 n ,1 - У 0 n ) =
(— [ ax + a^ + a3 + a^ — a3 a4 - a1 a2
( a 3 + a 4) - ( ax + a 2)
1 - m [1 + 7-----' ' -----7 ])
3 ( a 3 + a 4) - ( ax + a 2)
Finally, in order to avoid some of the flaws in methods such as Euclidean distance or the product of the coordinates [44], we propose the following algorithm:
According to the obtained centroid-points of TrIFNs A and B (4 points), we have eight parameters. In the proposed algorithm, the parameters of the memberships have direct effects in determining the rank of TrIFNs and non-membership's parameters has indirect effects on it.
-
IV. The Proposed Algorithm
We will describe two steps in our algorithm.
Let A ( X 0 a , У 0 a ) and A '( X 0 a , У 0 a ) be the centroid points of membership and non-membership functions of IFN A . Also, B ( x 0 ь , У 0 ь ) and B ‘ ( x 0 b , У 0 b ) are the centroid points of membership and non-membership functions of IFN B .
Step 1 Choose the centroid points of membership functions i.e. A ( x 0 a , y 0 a ),? B x 0 b , y 0 b ) :
If xoa < x^b then A < B , else if xOa > xQb then A > B, else if x0a = x0b and У0a < У0b then A < B, else if X0a = X0b and У0a > У0b then A > B, else if X0a = X0b and У0a = У0b then go to step 2.
Step 2 Choose the centroid points of non-membership functions i.e. A '( x 0 a , У 0 a ), B' xob , У 0 b ) :
|
If x 0 a < x 0 b |
then A |
> B , |
|
else if x 0 ' a |
> x 0 b |
then A < B , |
|
'' |
||
|
else if x ' |
= x 0 b |
and У 0 a < У 0 b then A > B |
|
else if x ' |
= x 0 b |
and У 0 a > У 0 b then A < B' |
|
else if x 0 ' a |
= x 0 b |
and У 0 a = У 0 b then A ~ B . |
In the following theorem, some useful properties of the proposed algorithm are proved:
Theorem 4.1
Let A , B and C be three TrIFNs, then:
-
i. A < B If and A > B , then A « B .
-
ii. A < B imply that A + C < B + C .
-
iii. If A < B and B < C , then A < C .
Proof
-
i. Assume that A < B and A > B . If, in the proposed algorithm, there exists at least one equation that is satisfied as " < " , then we have only A < B or A > B and it contradicts the assumptions. It means that x 0 a = x 0 b /■ У 0 a = У 0 b , x 0 a = x 0 b and У 0 a = У 0 b ,
finally A « B .
-
ii. Let A < B and C be an arbitrary IFN. Based on the defined properties for fuzzy addition,
A + C and B + C are IFNs which, are obtained from the same shifting A and B by C . Then, ranking order of initial IFNs doesn't vary, i.e. A + C < B + C .
-
iii. Assume that A < B and B < C , we show that the
case A ≮ C can't be satisfied. If A ≮ C then A > C or A = C .
If A > C , then C has at least one parameter, i.e. x , y , x ' or y ' , that is worse than its corresponding in A and finally, because of A < B , it is worse than its corresponding in B , i.e. C < B . It contradicts the assumption B < C .
In the other hand, if A = C , then, based on the proposed algorithm, x 0 a = x 0 c У 0 a = У 0c , x 0 a = x ^^c
, and уOa = уOc . Assumption A < B implies that A (and then, based on the above equality, C ) has at least one parameter which is worse than its analog inB . It means that C < B and contradicts the assumption B < C .
Then, we have A < C .
-
V. Numerical Examples
In this section we compare the proposed method and the other ones.
-
Example 1
Let
A=( 2,3,4,5; 0.2,0.7 ),
B = ( 1,1.5,2,2.5; 0.2,0.6 ) ,
C = ( 0,0.5,1,1.5;0.1,0.8), D = (1,3,5,7; 0.1; 0.7 ), E=(1.5,2.5,3.5,4.5; 0.3,0.6), be TrIFNs. These numbers express that the satisfaction degrees are very low and non-satisfaction degrees are high. We expect that a similar interpretation is provided from each composition of them. Table 1 shows the combined results of the different methods and it is easy to compare them.
The second column in the Table 1 shows, as the number of contributed values in summation increased, the satisfaction degree (membership degree) is increased and dissatisfaction degree is decreased.
If we multiply the above IFNs, we have Table 2.
Based on Def. 2.10, in the second column of Table 2, as the number of IFNs are increased, satisfaction degree tends to 0 , while dissatisfaction degree tends to 1 . Therefore, answering to the question " What are the satisfaction and non-satisfaction degrees of obtained IFNs from A + B + C + D + E and A . B . C . D . E ?" by our proposed method is closer to reality. It is because of the closeness of the obtained degrees to initial degrees in both addition and multiplication.
-
Example 2
Let W = ( 0.3,0.2,0.1,0.25,0.15 ) be the multiplication vector of the given numbers in the Exam. 2. Then, the total factor of them is obtained as in Table 3.
-
Example 3
Let
A = ([7,8,9,10; 0.1];[6.5,7.5,9.5,10; 0.8]),
B = ([5,6,7,8; 0.5];[4,5.5,7.5,9; 0.3]),
C = ([4,5.5,7.5,9; 0.3];[7.25,7.75,8.75,9; 0.6]),
D = ([2,3,4,5; 0.6];[1.5,2.5,4.5,5.5; 0.2])
and
E = ([5,6,7,8; 0.4];[4.5,5.5,7.5,8; 0.3])
be TrIFNs. Table 4 gives arithmetic operators on them based on some existing methods and the proposed method.
-
Example 4
Let
A 1 = ([(3,5,5,7); 0.6,0.4]),
A 2 = ((3,5,5,7); 0.5,0.3),
A 3 = ((5,7,9,10);0.5,0.3)
and
A 4 = ([(5,7,9,10); 0.5,0.4]) .
Then:
Table 1. The Sum Operator in IFNs
|
Sum |
Definition 2.10 |
Proposed method |
|
A + B |
( 3,4.5,6,7.5; 0.36,0.42 ) |
( 3,4.5,6,7.5; 0.2,0.648 ) |
|
A + B + C |
( 3,5,7,9; 0.424,0.336 ) |
( 3,5,7,9; 0.166,0.695 ) |
|
A + B + C + D |
( 4,8,12,16; 0.4816,0.2352 ) |
( 4,8,12,16; 0.15,0.696 ) |
|
A + B + C + D + E |
( 5.5,10.5,15.5,20.5; 0.63712,0.14112 ) |
( 5.5,10.5,15.5,20.5; 0.18,0.676 ) |
Table 2. The Product Operator in IFNs
|
Product |
Definition 2.10 |
Proposed method |
|
A . B |
( 2,4.5,8,12.5; 0.04,0.88 ) |
( 2,4.5,8,12.5; 0.2,0.65 ) |
|
A . B . C |
( 0,2.25,8,18.75; 0.004,0.976 ) |
( 0,2.25,8,18.75; 0.159,0.7 ) |
|
A . B . C . D |
( 0,6.75,40,131.25; 0.0004,0.9928 ) |
( 0,6.75,40,131.25; 0.1414,0.7 ) |
|
A . B . C . D . E |
( 0,16.875,140,590.625; 0.00012,0.99712 ) |
( 0,16.875,140,590.625; 0.164,0.68 ) |
Table 3. The Sum Operator IFNs with Positive Coefficients
|
Weighted Sum |
Definition 2.10 |
Proposed method |
|
wxA + wB + wC + w4D + w5E |
( 1.28,2.5,3.48,4.58; 0.18,0.63 ) |
( 1.28,2.5,3.48,4.58; 0.18,0.67 ) |
Table 4. The Arithmetic Operators on TrIFNs
|
Sum |
Wang’s method |
Nan’s method |
Proposed method |
|
A + B |
[12,14,16,18;0.55],[10.5,13,17,19;0.24] |
[ ;0.1],[ ;0.8] |
[ ;0.3],[ ;0.49] |
|
A + B + C |
[19.5, 22, 24.5, 27;0.64],[17.75, 20.75, 25.75, 28;0.144] |
[ ;0.1],[ ;0.8] |
[ ;0.267],[ ;0.524] |
|
A + B + C + D |
[21.5, 25, 29,32;0.856],[19.25, 23.25,30.25,33.5;0.00288] |
[ ;0.1],[ ;0.8] |
[ ;0.35],[ ;0.412] |
|
A + B + C + D + E |
[26.5,31,36,40;0.9136],[23.75,28.75,37.75, 41.5.;0.00864] |
[ ;0.1],[ ;0.8] |
[ ;0.36],[ ;0.387] |
|
Product |
|||
|
A.B |
[35, 48,63,80;0.05],[26, 41.25,71.25,90;0.86] |
[ ;0.5],[ ;0.3] |
[ ;0.223],[ ;0.55] |
|
A.B.C |
[262.5,384,535.5,720;0.01],[188.5,319.69,623.44,810;0.944] |
[ ;0.5],[ ;0.3] |
[ ;0.215],[ ;0.56] |
|
A.B.C.D |
[525,1152,2142,3600;0.006],[282.75,799.225,2805.48,4455;0.9712] |
[ ;0.6],[ ;0.2] |
[ ;0.495],[ ;0.475] |
Table 5. Ranking Order based on Li's Method
|
2 |
R ( A ) |
R ( A 2 ) |
R ( A 3 ) |
R ( A 4 ) |
Ranking |
|
0.2 |
1.67 |
1.44 |
2.01 |
2.05 |
A > a > A > A |
|
0.4 |
1.67 |
1.59 |
2.22 |
2.16 |
A > A > A > A |
|
0.6 |
1.67 |
1.75 |
2.45 |
2.28 |
A> A 4 > A 2 > A , |
|
0.8 |
1.67 |
1.92 |
2.69 |
2.4 |
A 3 > A 4 > A 2 > A . |
|
1 |
1.67 |
2.1 |
2.94 |
2.52 |
A 3 > A 4 > A 2 > A 1 |
-
1) Li's method [18] based on different values of X, gives different orders which are displayed in Table 5.
-
2) De's method [13] gives:
A>a >a =a .
-
3) Peng's method [26] for an optimistic decision maker ( 0 = 1) gives:
A > a > a > a .
-
4) Our proposed method gives the following order:
A > a > a > a .
-
Example 5
Let
A = ( ( 0.592,0.774,0.774,0.910 ) ;0.6,0.4) ,
A = ( ( 0.769,0.903,0.903,1 ) ; 0.4,0.5)
and
A = ( ( 0.653,0.849,0.849,0.956 ) ; 0.5,0.2)
be canonical IFNs. Based on the proposed method, we have A > A > A . This ranking order is similar to Peng's method [26] for an optimistic decision maker ( 0 = 1 ) .
-
VI. Conclusions
We know that the IFNs are expressed with membership and non-membership degrees. These characteristics will be changed during the arithmetic operations on IFNs. It is important that the changes are not far from reality. This significance is observed in our proposed method for arithmetic operations on IFNs. Moreover, ranking of IFNs is unavoidable in many practical applications of them. Although, some methods have been proposed for arranging IFNs, depending on the parameter and others, they do not report the correct order in special circumstances. We proposed to use center of gravity of membership and non-membership functions. It is help us to sort IFNs reality. In the future, we can apply proposed methods to solve practical problems such as MADM problems.
Acknowledgment
The authors would like to thank the associate editor and the anonymous reviewers whose comments are quite useful for us to improve the paper.
Список литературы Operations and Ranking Methods for Intuitionistic Fuzzy Numbers, a Review and New Methods
- K.T. Atanassov, Intuitionistic Fuzzy Sets, in: V. Sgurev, Ed., VII ITKR'S Session SO_a Jone 1983.
- K. T. Atanassov, Intuitionistic Fuzzy Sets Past, Present and Future, in EUSFLAT Conf., M. Wagenknecht and R. Hampel, Eds. University of Applied Sciences at Zittau/G¨orlitz, Germany, 12-19, 2003.
- K. T. Atanassov, Intuitionistic fuzzy sets and interval valued fuzzy sets, First Int. Workshop on IFSs, GNs, KE, London, 6-7 Sept., 1-7, 2006.
- K. T. Atanassov, G. Gargov, Interval valued intuitionistic fuzzy sets, Fuzzy Sets and Systems, 31, 343-349, 1989.
- K. T. Atanassov, Operators over interval valued intuitionistic fuzzy sets, Fuzzy Sets and Systems, 64, 159-174, 1994.
- K. T. Atanassov, Intuitionistic fuzzy sets, Fuzzy Sets and Systems, 20, 87-96, 1986.
- K. T. Atanassov, Intuitionistic Fuzzy Sets: Theory and Applications, Springer-Verlag,1999.
- A. I. Ban, D. A. Tuse, Trapezoidal/triangular intuitionistic fuzzy numbers versus interval-valued trapezoidal/triangular fuzzy numbers and applications to multicriteria decision making methods, 18th Int. Conf. on IFSs, Sofia, 10-11 May 2014.
- I. Beg. T. Rashid, Multi-criteria trapezoidal valued intuitionistic fuzzy decision making with Choquet integral based TOPSIS, OPSEARCH, 51, 98-129, 2014.
- H. Bustincee, P. Burillo, Vague sets are intuitionistic fuzzy sets, Fuzzy Sets Systems, 79,403-405, 1996.
- Z. Chen, W. Yang, A new multiple attribute group decision making method in intuitionistic fuzzy setting, Applied Mathematical Modeling, 35, 4424-4437, 2011.
- T. Y. Chen, H. P. Wang, Y. Y. Lu, A multicriteria group decision-making approach based on interval-valued intuitionistic fuzzy sets: A comparative perspective, Expert Systems with Applications, 38, 7647-7658, 2011.
- P. K. De, D. Das, A study on ranking of trapezoidal intuitionistic fuzzy numbers, International Journal of Computer Information Systems and Industrial Management Applications, ISSN 2150-7988, 6, 437-444, 2014.
- W. L. Gau, D. J. Buehrer, Vague Sets, IEEE Transaction on system, Man, and Cybernetics, 23, 2, 610-614, 1993.
- A. Kumar, M. Kaur, A ranking approach for intuitionistic fuzzy numbers and its application, Journal of applied research and technology, 11, 3, 381-396, 2013.
- D. F. Li, Multiattribute decision making method based on generalized OWA operators with intuitionistic fuzzy sets, Expert Systems with Applications, 37, 8673-8678, 2010.
- D. F. Li, J. X. Nan, M. J. Zhang, Ranking method of triangular intuitionistic fuzzy numbers and application to decision making, International Journal of Computational Intelligence Systems, 3, 5, 522-530, 2010.
- D. F. Li, A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems, Computers and Mathematics with Applications, 60, 1557-1570, 2010.
- D. F. Li, A note on using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly, Microelectronics Reliability 48, 17-41, 2008.
- F. Liu, X. H. Yuan, Fuzzy number intuitionistic fuzzy set, Fuzzy Systems and Mathematics, 21, 88-91, 2007.
- J. X. Nan, D. F. Li, M. J. Zhang, A lexicographic method for matrix games with payoffs of triangular intuitionistic fuzzy numbers, International Journal of Computational Intelligence Systems, 3, 280-289, 2010.
- V. L. G. Nayagam, G. Venkateshwari, G. Sivaraman, Rank ing of intuitionistic fuzzy numbers, Applied Soft Computing, 11, 3368-3372, 2011.
- V. L. G. Nayagam, S. Muralikrishnan, G. Sivaraman, Multi-criteria decision-making method based on interval-valued intuitionistic fuzzy sets, Expert Systems with Applications 38, 1464-1467, 2011.
- V. L. G. Nayagam, S. Muralikrishnan, G. Sivaraman, Ranking of interval-valued intuitionistic fuzzy sets, Applied Soft Computing 11, 3368-3372, 2011.
- R. Parvathi , C. Malathi, Arithmetic operations on symmetric trapezoidal intuitionistic fuzzy numbers, International Journal of Soft Computing and Engineering (IJSCE), ISSN: 2231-2307, 2, 2, 2012.
- Z. Peng, Q. Chen, A new method for ranking canonical intuitionistic fuzzy numbers, Proceedings of the International Conference on Information Engineering and Applications (IEA) 2012, Lecture Notes in Electrical Engineering, 216, 609-616, 2013.
- W. J. Qiang, Z. Zhong, Aggregation operators on intuitionistic trapezoidal fuzzy number and its application to multi-criteria decision making problems, Journal of Systems Engineering and Electronics, 20, 2, 321-326, 2009.
- W. J. Qiang, Z. Zhong, Programming method of multicriteria decision-making based on intuitionistic fuzzy number with incomplete certain information, Control and decision, 23 , 10, 1145-1148, 2008.
- S. S. Roseline, E. C. H. Amirtharaj, A new ranking of intuitionistic fuzzy numbers with distance method based on the circumcenter of centroids, International Journal of Applied Mathematics & Statistical Sciences (IJAMSS) 2, 4, 37-44, 2013.
- A. Solairaju, P. J. Robinson, S. R. Kumar, Interval valued intuitionistic fuzzy MAGDM problems with OWA entropy weights, International Journal of Mathematics Trends and Technology, 9, 2, 2014.
- E. Szmidt and J. Kacprzyk, Concept of distances and entropy for intuitionistic fuzzy sets and their applications in group decision making, Sixth Int. Conf. on IFSs, Varna, 13-14 Sept. 2002, NIFS, 8, 3, 11-25, 2002.
- C. Tan, X. Chen, Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making, Expert Systems with Applications, 37, 149-157, 2010.
- S. P. Wan, Power average operators of trapezoidal intuitionistic fuzzy numbers and application to multi-attribute group decision making, Applied Mathematical Modeling 37, 4112-4126, 2013.
- J. Q. Wang, R. Nie, H. Y. Zhang, X. H. Chen, New operators on triangular intuitionistic fuzzy numbers and their applications in system fault analysis, Information Sciences, 251, 79-95, 2013.
- Y. M. Wang, J.B Yanga, D. L. Xua, K. S. Chinc, On the centroids of fuzzy numbers, Fuzzy Sets and Systems 157, 919-926, 2006.
- C. P. Wei, A new method for ranking intuitionistic fuzzy numbers, International Journal of Knowledge and Systems Science, 2, 43-49, 2011.
- Z. Xu, X. Cai, Intuitionistic Fuzzy Information Aggregation: Theory and Applications, Science Press Beijing and Springer-Verlag Berlin Heidelberg 2012, ISBN 978-7-03-033321-6 Science Press Beijing.
- Z. Xu, Intuitionistic Fuzzy Aggregation Operators, IEEE Transactions on Fuzzy Systems, 15, 6, 2007.
- Z. Xu, Intuitionistic preference relations and their application in group decision making, Information Sciences, 177 , 2363-2379, 2007.
- Z. Xu, M. Xia, Induced generalized intuitionistic fuzzy operators, Knowledge-Based Systems 24, 197-209, 2011.
- Z. Xu, Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making, Control and Decision, 22, 215-219, 2007.
- J. Ye, Prioritized aggregation operators of trapezoidal intuitionistic fuzzy sets and their application to multicriteria decision-making, Journal of Neural Computing and Applications, 25, 6, 1447-1454, 2014.
- D. Yu, Intuitionistic trapezoidal fuzzy information aggregation methods and their applications to teaching quality evaluation, Journal of Information & Computational Science 10:6, 1861-1869, 2013.
- V. F. Yu, L. Q. Dat, N. H. Quang, T. A. Son, S.Y. Chou, A. C. Lin, An extension of fuzzy TOPSIS approach based on centroid-index ranking method, Scientific Research and Essays, 7, 14, 1485-1493, 2012.
- L. A. Zadeh, Fuzzy sets, Information and Control, 8, 338-353, 1965.
- M. J. Zhang, J. X. NAN, A compromise ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems, Iranian Journal of Fuzzy Systems, 10, 6, 21-37, 2013.


