Операторные методы поиска вырожденных экстремальных управлений в линейных по управлению задачах оптимального управления

Распространенным подходом к решению задач оптимального управления является поиск экстремального решения, т. е. удовлетворяющего необходимым условиям оптимальности. Классическим подходом является поиск решения краевой задачи принципа максимума [1-3] с общеизвестными трудностями. Альтернативный подход состоит в построении итерационных процессов улучшения управления, сходящихся в том или ином смысле к экстремальному решению. Здесь наиболее известны градиентные методы [2; 3]. В последние десятилетия активно развиваются методы нелокального улучшения управления [4].

В работах [5; 6] рассматривается новый подход к поиску экстремального решения, основывающий на представлении необходимых условий оптимальности управления в форме операторных задач о неподвижной точке в пространстве допустимых управлений. Такое представление дает возможность применить и модифицировать известные методы неподвижных точек для поиска экстремальных решений. Подход неподвижных точек для конструирования условий оптимальности и улучшения управления развивается более десяти лет для различных классов непрерывных, дискретных и дискретно-непрерывных задач оптимального управления, в том числе включающих терминальные и фазовые ограничения, смешанные управляющие функции и параметры, нефиксированное время окончания процесса управления и другие особенности.

Поиск экстремальных решений существенно усложняется в вырожденных задачах оптимального управления, в которых необходимые условия оптимальности в форме классического принципа максимума не позволяют определять экстремальные решения. В частности, метод краевой задачи принципа максимума и градиентные методы становятся не эффективными в вырожденных задачах.

В настоящей работе в классе линейных по управлению задач оптимального управления рассматриваются методы поиска экстремальных управлений, удовлетворяющих операторным формам принципа максимума в виде задач о неподвижной точке. Для рассматриваемого класса задач характерным является свойство вырожденности классического принципа максимума во многих физико-технических, эколого-экономических и других актуальных приложениях.

Целью работы является анализ рассматриваемых методов поиска вырожденных экстремальных управлений, удовлетворяющих операторным формам принципа максимума. Анализируются и сравниваются с известными понятиями условия вырожденности экстремальных управлений на основе рассматриваемых операторных форм принципа максимума. Проводится сравнительный анализ предлагаемых операторных методов принципа максимума с известными методами. Исследуется сравнительная эффективность предлагаемых операторных методов принципа максимума на модельном примере вырожденной задачи рассматриваемого класса.

1 Вырожденные экстремальные управления

Рассматривается класс линейных по управлению задач оптимального управления:

Ф(и) = ф(x(t,)) + J F(x(t),и(t),t)dt ^ inf,(1)

Tu

x(t) = f (x(t),и(t),t), x(10) = x°, и(t) e U c Rm, t e T = [t0,t1],(2)

в котором функция ф(x) непрерывно-дифференцируема на Rn, функции f (x,и,t) и F(x, и,t) непрерывно-дифференцируемы по переменной x, линейны по переменной u и непрерывны по переменной t на множестве Rn х U x T. В качестве допустимых управлений и(t) = (и 1(t),...,ит (t)) рассматривается множество V кусочно-непрерывных функций на интервале T со значениями в компактном и выпуклом множестве U c Rm. Начальное состояние x0 и интервал T фиксированы. Используется общее обозначение линейных по управлению функций f (x,и,t) и F(x, и,t) для удобства и простоты представления конструкций операторных методов принципа максимума.

Функция Понтрягина и стандартная сопряженная система с сопряженной переменной у в задаче (1), (2) соответственно представляются в следующей форме:

Н ( у , x , и , t ) = < у , f ( x , и , t ) >- F ( x , и , t ),       у e R n ;

^{у (} t ) = ^- H x ⁽ У ⁽ t ). ^{x (} t ). ^{и (} t ). t ),        t e T , у ⁽ t i ) = -ф _х ⁽ x ⁽ t ^.      ⁽³⁾

Обозначим x ( t , v ), t e T — решение системы (2) для допустимого управления v e V ; у ( t , v ), t e T — решение стандартной сопряженной системы (3) при x ( t ) = x ( t , v ), и ( t ) = v ( t ) .

Известное [1-4] необходимое условие оптимальности (принцип максимума) для управления и e V в классе задач (1), (2) можно записать в форме:

и ( t ) = arg max ( Н_я ( у ( t , и ), x ( t , и ), и ( t ), t ), w ^, t e T .           (4)

w ∈ U

С помощью отображения и *, определяемого соотношением и * (у, x, t) = argmax H (у, x, w, t), у e Rn, x e Rn, t e T, w∈U условие (4) можно представить в следующем виде:

и ( t ) = и * ( у ( t , и ), x (t , и ), t ), t e T .

Условие (4) с помощью операции проектирования можно записать в эквивалентной форме с параметром a >  0 :

и ( t ) = P U ( и ( t ) + аН_и ( у ( t , и ), x ( t , и ), и ( t ), t ) ) , t e T .           (5)

Определим отображение и ^а с параметром a >  0 на основе соотношения:

и ^а ( у,x , w , t ) = P U ( w + аН_и ( у , x , w , t ) ) , x e R n , у e R n , w e U , t e T .

С помощью отображения u a принцип максимума в проекционной форме (5) можно записать в виде:

u ( t ) = u a (у(t , u ), x ( t , u ), u ( t ), t ),        t e T .

Управление u e V , удовлетворяющее необходимым условиям оптимальности (4) и (5), называется экстремальным.

Рассмотрим функцию переключения g ( у , x , t ) = H_u ( у , x , u , t ).

Управление u e V называется вырожденным, если для этого управления существует интервал времени [ # , , 0 2 ] с T ненулевой меры, на котором выполняется условие g(у(t , u ), x ( t , u ), t ) = 0.

Для вырожденного управления условия (4) и (5) на интервале вырожденности выполняются тривиально и не могут служить для определения экстремального управления на интервале вырожденности. В этом смысле условия принципа максимума (4) и (5) вырождаются на вырожденном экстремальном управлении.

Задача (1), (2) называется вырожденной, если существует хотя бы одно вырожденное экстремальное управление.

В соответствии с работой [6] определим отображения X , Т , V * , V a , a >  0 :

X ( u ) = x , u e V , x ( t ) = x ( t , u ), t e T ,

T ( u ) = у , u e V , у ( t ) = у ( t , u ), t e T ,

V * ( у , x ) = v * , у e C ( T ), x e C ( T ), v * ( t ) = u * ( у ( t ), x ( t ), t ), t e T ,

V ^a ( у , x , u ) = v a , у e C (T ), x e C ( T ), u e V , v a ( t ) = u a ( у ( t ), x(t ), u (t ), t ), t e T , где C ( T ) — пространство непрерывных на T функций.

Рассмотрим оператор X * :

X * ( у ) = x , у e C (T ), где x ( t ), t e T — решение задачи Коши:

x ( t ) = f ( x ( t ), u * ( у ( t ), x ( t ), t ), t ), x ( t o ) = x ⁰.

Для a >  0 рассмотрим оператор X a :

Xa (у, u) = xa,     у e C(T), u e V , где xa (t), t e T — решение задачи Коши:

^x ( t ) = f ( x ( t ), ua (у(t ), x ( t ), u ( t ), t ), t ), x ( 1 0 ) = x ⁰.

Введем оператор Т ' :

Т * ( x ) = у , x e C ( T ), где у ( t ), t e T — решение сопряженной задачи Коши:

у ( t ) = - H x ( у ( t ), x ( t ), u * ( у ( t ), x ( t ), t ), t ), у (1 1 ) = - y x ( x ( 1 1 )) .

Для a >  0 введем оператор T a :

Т a (x, u) = ya ,      x e C (T), u e V , где va (t), t e T — решение сопряженной задачи Коши:

V ( t ) = - H x (у ( t ), x ( t ), u ^a (v(t ), x ( t ), u ( t ), t ), t ), у ( 1 1 ) = -Ф_х ( x ( t , )) .

В соответствии с [6] следующие операторные задачи о неподвижной точке являются эквивалентными условиям принципа максимума (4) и (5):

u = V * (Т( u ), X (u)), u = V * (Т( u), X * (Т( u))),(7)

u = V * (T* (X (u)), X (u)), u = V a (T( u), X (u), u),(9)

u = V a (T( u), X a (T(u), u), u),(10)

u = V a (Ta (X (u), u), X (u), u).(11)

Вырожденность операторных форм принципа максимума (6)-(11) определяется на основе соответствующих эквивалентных поточечных форм этих условий.

Очевидно, что поточечными формами операторных принципов максимума (6) и (9) являются условия (4) и (5) соответственно, вырожденность которых определяется выше на основе функции переключения g ( у , x , t ).

Операторный принцип максимума (7) в поточечной форме имеет следующий вид:

u ( t ) = u * ( у ( t , u ), x ( t ), t ), t e T , где x ( t ), t e T является решением специальной задачи Коши:

x ( t ) = f ( x ( t ), u * ( у ( t , u ), x ( t ), t ), t ), x ( t o ) = x ⁰.                    (12)

Введем функцию переключения g 1 ( x , t ) = g( у ( t , u ), x , t ).

Если для управления u e V существует интервал времени [ У , , 0 ₂ ] с T ненулевой меры, на котором выполняется условие g 1 ( x ( t ), t ) = 0 , где x ( t ) является решением специальной задачи Коши (12), то это управление назовем вырожденным в смысле функции g 1 ( x , t ).

Для вырожденного управления в смысле функции g 1 ( x , t ) соотношение u ( t ) = u * ( у ( t , u ), x ( t ), t ) не может служить для определения экстремального управления, входящего в правую часть системы (12) на интервале вырожденности. В этом смысле принцип максимума (7) вырождается на таком вырожденном экстремальном управлении.

Покажем, что понятия вырожденности экстремальных управлений, удовлетворяющих условию (4) на основе функции g(у,x,t) и удовлетво- ряющих условию (7) на основе функции g1(x, t), являются эквивалентными. Имеет место следующее утверждение.

Предложение 1. Вырожденное экстремальное управление u е V на основе функции переключения g ( у , x , t ) является вырожденным экстремальным управлением на основе функции переключения g 1 ( x , t ) и наоборот. При этом соответствующие интервалы вырожденности совпадают.

Действительно, пусть экстремальное управление и е V является вырожденным на основе функции переключения g ( у , x , t ), т. е. g(у(t , и ), x ( t , и ), t ) = 0, t е [ Д 1 , Д ₂] с T . В силу экстремальности управления и е V имеем и ( t ) = и * ( у ( t , и ), x ( t , и ), t ), t е T . Следовательно, функция x ( t ) = x ( t , и ), t е T удовлетворяет задаче Коши:

x( t ) = f ( x ( t ), и * ( у ( t , и ), x ( t ), t ), t ), x ( t o ) = x ⁰.

Отсюда получаем, g 1 ( x ( t ), t ) = g(у(t , и ), x ( t , и ), t ) = 0, t е [ 0 1 , 0 ₂] с T .

Обратно, пусть экстремальное управление и е V является вырожденным на основе функции переключения     g 1 ( x , t ), т. е.

g j ( x ( t ), t ) = g (у( t , и ), x ( t ), t ) = 0, t е [ Д 1 , Д ₂] с T , где x ( t ), t е T является решением задачи Коши (12). В силу системы (12) и условия экстремальности и ( t ) = и * ( у ( t , и ), x ( t ), t ) имеем x ( t ) = x ( t , и ), t е T . Следовательно, получаем 0 = g , ( x ( t ), t ) = g ( у ( t , и ), x ( t , и ), t ), t е [ 0 , , 0 2 ] с T .

Аналогично функция g 1 ( x , t ) определяет вырожденность поточечной формы операторного принципа максимума (10):

и ( t ) = и ^а ( у ( t , и ), x ( t ), и ( t ), t ) , t е T , где x ( t ), t е T является решением специальной задачи Коши:

;x ( t ) = f ( x ( t ), и^а ( у ( t , и ), x ( t ), и ( t ), t ), t ), x ( 1 0 ) = x ⁰.      (J 3)

Если для управления и е V существует интервал времени [ Д , 0 ₂ ] с T ненулевой меры, на котором выполняется условие g 1 ( x ( t ), t ) = 0 , где x ( t ) является решением специальной фазовой задачи Коши (J3), то это управление назовем вырожденным в смысле функции g 1 ( x , t ).

Имеет место аналогичное Предложению j утверждение.

Предложение 2 . Вырожденное экстремальное управление на основе функции g(у,x , t ), удовлетворяющее условию (5), является вырожденным экстремальным управлением на основе функции g 1 ( x , t ), удовлетворяющим условию (j0), и наоборот. При этом соответствующие интервалы вырожденности совпадают.

Определим вырожденность операторного принципа максимума (8) с соответствующей поточечной формой, имеющей вид:

и (t) = и * (у( t), x (t, и), t), t е T, где у(t), t е T является решением специальной сопряженной задачи Коши:

у ( t ) = - H x (у ( t ), x ( t,u ), u * ( у ( t ), x ( t,u ), t ), t ), у ( t J = -ф х ( x ( t 1 , u )). (14)

Введем функцию переключения g₂( у ,t ) = g( у ,x ( t , u ), t ).

Если для управления u е V существует интервал времени [ 0 1 , 0 ₂ ] с T ненулевой меры, на котором выполняется условие g₂(у(t ), t ) = 0, где у ( t ) является решением специальной сопряженной задачи Коши (14), то это управление назовем вырожденным в смысле функции g ₂( у , t ).

Для вырожденного управления в смысле функции g₂( у ,t ) соотношение u ( t ) = u * ( у ( t ), x ( t , u ), t ) не может служить для определения экстремального управления, входящего в правую часть системы (14) на интервале вырожденности. В этом смысле принцип максимума (8) вырождается на таком вырожденном экстремальном управлении.

Предложение 3 . Вырожденное экстремальное управление u е V на основе функции переключения g ( у , x , t ), удовлетворяющее условию (4), является вырожденным экстремальным управлением на основе функции переключения g ₂( у , t ), удовлетворяющим условию (8), и наоборот. При этом соответствующие интервалы вырожденности совпадают.

Действительно, пусть экстремальное управление u е V , удовлетворяющее условию (4), является вырожденным на основе функции переключения g ( у , x , t ), т. е. g(у(t , u ), x ( t , u ), t ) = 0, t е [ 0 , , 0 ₂] с T . В силу экстремальности управления u е V имеем u ( t ) = u * ( у ( t , u ), x(t , u ), t ), t е T . Следовательно, функция у ( t ) = у ( t , u ), t е T удовлетворяет сопряженной задаче Коши:

у ( t ) = - H x (у ( t ), x ( t , u ), u * ( у ( t ), x ( t , u ), t ), t ), у ( 1 1 ) = - ф x ( x ( 1 1 , u )).

Отсюда получаем g ₂( у ( t ), t ) = g(у(t , u ), x ( t , u ), t ) = 0, t е [ 0 1 , 0 ₂] с T .

Обратно, пусть экстремальное управление u е V , удовлетворяющее условию (8), является вырожденным на основе функции переключения g 2 ( у , t ), т. е. g 2 (у( t ), t ) = g (у( t ), x ( t , u ), t ) = 0, t е [^Д] с T , где у ( t ), t е T является решением задачи Коши (14). В силу сопряженной системы (14) и условия экстремальности u ( t ) = u * ( у ( t ), x ( t , u ), t ) имеем у ( t ) = у ( t , u ), t е T . Следовательно, получаем:

0 = g 2 ( у ( t ), t ) = g(у(t , u ), x ( t , u ), t ), t е [ 0 ₁, 0 2 ] с T .

Аналогично функция g ₂( у , t ) определяет вырожденность поточечной формы операторного принципа максимума (11):

u ( t ) = u a (у(t ), x ( t , u ), u ( t ), t ) , t е T , где у ( t ), t е T является решением специальной сопряженной задачи Коши:

У ( t ) = - H x (у ( t ), x ( t , u ), u a ( у ( t ), x ( t , u ), u ( t ), t ), t ), у ( t У = -Ф х ( x ( t„u )). (15)

Если для управления u e V существует интервал времени [ 0 1 , 0 ₂ ] с T ненулевой меры, на котором выполняется условие g ₂( у ( t ), t ) = 0, где у ( t ) является решением специальной сопряженной задачи Коши (15), то это управление назовем вырожденным в смысле функции g ₂( у , t ).

Также имеет место аналогичное Предложению 3 утверждение.

Предложение 4 . Вырожденное на основе функции g(у,x , t ) экстремальное управление, удовлетворяющее условию (5), является вырожденным на основе функции g₂( у ,t ) экстремальным управлением, удовлетворяющим условию (11), и наоборот. При этом соответствующие интервалы вырожденности совпадают.

Таким образом, для поиска вырожденных в классическом смысле (на основе функции переключения g(у,x , t )) экстремальных управлений, удовлетворяющих условиям классического принципа максимума (условия (4) и (5)), можно применять методы, основанные на операторных формах принципа максимума (6)-(11).

2 Операторные методы принципа максимума

Следуя работе [6], для поиска вырожденных экстремальных управлений рассмотрим итерационные процессы метода простой итерации с индексом к >  0 с заданным начальным управлением u ⁰ e V при к = 0 для численного решения соответствующих задач о неподвижной точке (6)-

(11):

uk+1 = V * (^( uk), X (uk)), uk+1 = V * (^( uk), X * (^( uk))),(17)

uk+1 = V* (^* (X(uk)),X(uk)),(18)

uk+1 = Va (Щ( uk), X (uk), uk), uk+1 = Va (Щ( uk), X a (^(uk), uk), uk),(20)

uk+1 = Va (Щa (X(uk),uk),X(uk),uk).(21)

Сходимость указанных итерационных процессов можно анализировать на основе известного принципа сжимающих отображений, принципа возмущений и принципа продолжения решения по параметру аналогично работам [5; 6].

Процесс (16) в поточечной форме имеет вид:

u^{k + 1}( t ) = u * ( у ( t , u^k ), x ( t , u^k ), t ) , t e T .                    (22)

Этому процессу в пространстве управлений эквивалентно соответствует известный метод последовательных приближений Крылова — Черноусько в пространстве фазовых и сопряженных состояний для решения краевой задачи принципа максимума. Отметим, что таким образом возникает возможность анализа сходимости метода

Крылова — Черноусько с помощью анализа сходимости итерационного процесса (22).

Процесс (19) в поточечной форме имеет вид:

u k ^{+ 1}( t ) = u ^a ( у ( t , u k ), x ( t , u k ), u k ( t ), t ) , t e T .           (23)

В отличие от известного метода проекции градиента [2; 3] на каждой итерации процесса (23) не производится варьирование полученного приближения управления u k ^{+ 1}( t ) с целью улучшения значения функционала Ф ( u k ). Это является существенным фактором повышения вычислительной эффективности итерационного процесса (23), оцениваемой суммарным количеством расчетных фазовых и сопряженных задач Коши, по сравнению с методом проекции градиента. Сходимость процесса (23) к экстремальному управлению можно обосновать при достаточно малых значениях параметра проектирования a >  0 аналогично [5; 6].

Процесс (17) на основе операции максимизации в поточечной форме имеет вид:

u k ( t ) = u * ( у ( t , u k ), x ( t ), t ) , t e T , где x ( t ), t e T является решением специальной задачи Коши: x ( t ) = f ( x ( t ), u * ( у ( t , u k ), x ( t ), t ), t ), x ( t o ) = x ⁰.

Процесс (17) в поточечной форме можно записать в неявном виде:

u k ^{+ 1}( t ) = u * ( у ( t , u k ), x ( t , u k ^{+ 1}), t ) , t e T .                  (24)

Процесс (20), являющийся проекционным аналогом процесса (17), в поточечной форме имеет вид:

u k ^{+ 1} ( t ) = u ^a (у ( t , u k ), x ( t ), u k ( t ), t ) , t e T , где x ( t ), t e T является решением специальной задачи Коши:

• *( t ) = f ( x ( t ), u ^a ( у ( t , u k ), x ( t ), u k ( t ), t ), t ), x ( t o ) = x ⁰.

Процесс (20) можно также записать в неявной поточечной форме:

u k ^{+ 1}( t ) = u ^a (у(t , u k ), x ( t , u k ^{+ 1}), u k ( t ), t ) , t e T .        (25)

Процесс (18) в поточечной форме имеет вид:

uk+1(t) = u* (у(t),x(t,uk),t), t e T, где у(t), t e T является решением специальной задачи Коши:

у ( t ) = - H x ( у ( t ), x ( t , u k ), u * ( у ( t ), x ( t , u k ), t ), t ), у ( t 1 ) = - ^ x ( x ( t 1 , u k )).

Поточечная форма процесса (21), являющегося проекционным аналогом процесса (18), имеет вид:

u k ^{+ 1}( t ) = u ^a (у ( t ), x ( t , u k ), u k ( t ), t ) , t e T , где у ( t ), t e T является решением специальной сопряженной задачи Коши:

У ( t ) = - H x (у ( t ), x ( t , u k ), u a (у(t ), x ( t , u k ), u k ( t ), t ), t ) ,

• У ⁽ t 1 ) = ^-Ф x ^{( x (} t 1 , u k )b

В классе билинейных задач оптимального управления, в котором функция ф ( х ) линейна на R n , функции f ( х , u , t ) и F ( х , u , t ) линейны по переменной x , линейны по переменной u и непрерывны по переменной t на множестве R n х U х T , процессы (18) и (21) в поточечной форме можно соответственно также представить в неявном виде:

u k ^{+ 1}( t ) = u * ( у ( t , u k ^{+ 1}), x ( t , u k ), t ), t _e T ,                 (26)

u k ^{+ 1}( t ) = u a (у(t , u k ^{+ 1}), x ( t , u k ), u k ( t ), t ), t e T .             (27)

В указанном классе билинейных задач оптимального управления неявным процессам (24) и (26) соответствуют известные [4] x -метод нелокального улучшения управления и ψ -метод нелокального улучшения управления соответственно. Проекционным неявным процессам (25) и (27) также соответствуют известные [4] проекционные нелокальные методы улучшения.

Таким образом, в классе билинейных задач оптимального управления операторные методы (18)-(21) становятся эквивалентными известным методам нелокального улучшения управления, имеющими возможность строгого улучшения экстремальных управлений, в том числе вырожденных экстремальных управлений. В работе [4] сходимость указанных методов улучшения управления анализируется по невязке принципа максимума.

В нелинейных по состоянию задачах оптимального управления (1), (2) итерационные процессы (18)-(21) не имеют известных или близких аналогов и являются принципиально новыми для поиска экстремальных управлений. При этом на каждой итерации этих процессов улучшение управления не гарантируется.

Трудоемкость реализации одной итерации процессов (16)-(21) составляет две задачи Коши. Последовательные приближения итерационных процессов (16)-(21) характеризуются нелокальностью приближений управления и отсутствием трудоемкой операции варьирования управления для удовлетворения условия строгого улучшения по функционалу. Указанные свойства итерационных процессов (16)-(21) являются важными для повышения эффективности поиска экстремальных управлений.

3 Модельный пример вырожденной задачи

Эффективность операторных методов поиска вырожденных экстремальных управлений в рассматриваемом линейном по управлению классе задач оптимального управления иллюстрируется на примере известной вырожденной модельной задачи управления системой спинов квантовых частиц [7], которая может быть представлена в следующем виде:

Ф ( и ) = 1 - Хх ( t 1 ), Lx ( t 1 )) ^ min , x 1 ( t ) = и ( t ) x ₃ ( t ) + x ₄ ( t ), x ₂ ( t ) = x ₃ ( t ) - и ( t ) x ₄ ( t ), x ₃ ( t ) = - и ( t ) x 1 ( t ) - x ₂ ( t ), x ₄ ( t ) = - x 1 ( t ) + и ( t ) x ₂ ( t ),

^Л a ' + b j      a 1 a ₂ + bb ₂        0        a 1 b₂ - b 1 a ₂

aa + bK a 2 + b ²     a₂b. - La.      0

L 1 2      1 2      2      2           2 1      2 1

0        a ₂ b 1 - b ₂ a 1      b + a j      b 1 b₂ + a 1 a ₂

v a b2 - b1 a 2     0       b1b2 + a a2     b22 + a 2 y x1(0) = ^ x 2(0) = ^, x3(0) = 0, x4(0) = 0, t e T = [0, t1], t1 = 1.5.

a 1 = 0.6, b 1 =- 0.3, a ₂ = 0.1, b ₂ = 7054.

Вектор x ( t ) описывает состояние квантовой системы, функция

и ( t ) e U = [ - 30,30] характеризует воздействие внешним полем.

Функция Понтрягина в задаче имеет вид:

H ( v , x , и , t ) = v ₁ ( ux ₃ + x ₄) + v ₂( x ₃ - ux ₄) + V ₃( - ux₁ - x ₂) + v ₄( - x 1 + ux ₂).

Стандартная сопряженная система записывается в виде: V1 (t) = и (t)V3 (t) + V4( t), V 2 (t) = V3 (t) - и (t)V4 (t), t e T,

V 3 ( t ) = - и ( t ) V 1 ( t ) - V 2 ( t ), V 4 ( t ) = и ( t )V 2 ( t ) - V 1 ( t ),

V 1 ⁽ t i ) = ²⁽ a l^{2 + b} 1^{2 ) x} i ( t i ) ^{+ 2(} a l a 2 ^{+ b} 1 ^b 2 ) x 2 ⁽ t i ) ^{+ 2(} a l ^b 2 ^{- b} 1 a 2 ) x 4 ⁽ t i ) , V 2 ⁽ t i ) = ²⁽ a i a 2 ^{+ b} 1 ^b 2 ) ^x i ( t i ) ^{+ 2(} a 22 ^{+ b} 2^{2 )} x 2 ⁽ t i ) ^{+ 2(} a 2 ^b 1 ^{- b} 2 a i ) x 3 ⁽ t 1 ) , V ₃( t 1 ) = 2( a ₂ b 1 - b ₂ a 1 ) x ₂( t 1 ) + 2( b 1² + a 1² ) x ₃( t 1 ) + 2( b 1 b ₂ + a 1 a ₂) x ₄( t 1 ), V 4 ⁽ t i ) = ^{2( a} i b 2 ^- b i ^a 2 ) ^x i ⁽ t i ) ^{+ 2( b} 1 ^b 2 ^{+ a} i ^a 2 ) ^x 3 ⁽ t i ) ^{+ 2(} b 2^{2 + a} 2² ) x 4 ⁽ t i ) ^.

Условие принципа максимума (4) имеет вид: и ( t ) = и *( v ( t , и ), x ( t , и ), t ), t e T ,

'+30,     g(V, x) > 0, и * (v, x, t) = ^-30,     g (v, x) < 0,

g ( v , x ) = V 1 x ₃ - V ₂ x ₄ - V ₃ x 1 + V ₄ x ₂ .

, w e U ,   g ( v , x ) = 0,

Вырожденные интервалы экстремальных управлений определяются тождеством g ( v ( t , и ), x ( t , и )) = 0.

В работе [7] для расчета рассматриваемой задачи оптимального управления применялся глобальный метод Кротова, эффективность которого сравнивалась с известным градиентным методом. В качестве стартового начального приближения управления для указанных методов выбиралось управление, определяемое из физических соображений:

u ( t ) = tg (2 γ (2 t - 1.5)), t ∈ T , γ =- ¹ ₃ arctg ( - 30) .

При этом было получено расчетное приближение экстремального управления с значением целевого функционала Ф ∗ ≈ 0.000952 . Вырожденный интервал расчетного управления равен [0.0667, t ₁]. Точность вырождения условия принципа максимума в смысле равенства нулю модуля функции переключения g ( ψ , x ) на итерационных приближениях методов принималась равной значению ε _v = 10 -³ .

В рассматриваемых операторных методах принципа максимума численное решение фазовых и сопряженных задач Коши осуществлялось с помощью модуля DIVPRK из библиотеки IMSL языка программирования FortranPowerStation 4.0 [8]. Данный модуль реализует метод Рунге — Кутта — Вернера (5–6) порядка точности. Значения фазовых, сопряженных и управляемых переменных запоминались в узлах заданной равномерной сетки T_h с шагом дискретизации h = 10 - ⁵ . В промежутках между соседними узлами сетки T_h значение управления принималось постоянным и равным значению в левом узле.

Итерационные процессы последовательных приближений управления осуществлялись до выполнения следующего критерия остановки:

max{Iuk+1(t) - uk(t)I,t∈Th}≤εm, где εm = 10-3 — заданная точность расчета операторной задачи о неподвижной точке.

Операторный метод (16) .

Итерационный процесс (16) в поточечной форме при k ≥ 0 имеет вид: u^k + ¹ ( t ) = u ^*( ψ ( t , u^k ), x ( t , u^k ), t ) , t ∈ T .

Для адекватного сравнения эффективности результатов итерационного процесса (16) с результатами, полученными в [7], равенство нулю функции переключения g ( ψ , x ) на итерационных приближениях также оценивалось с точностью ε _v = 10 -³ . В этом случае значение управления u^k + ¹( t ) на вырожденном интервале определялось по правилу дифференцирования тождества g ( ψ ( t , u ), x ( t , u )) ≡ 0 и вычисления вырожденного управления u ( t ) в силу фазовой и сопряженной систем.

На рисунке 1 представлено конечное расчетное управление v 1( t ), t ∈ T , полученное методом (16) с указанного выше начального управления u ( t ) с количеством итераций улучшения, равным 18, и значением функционала Ф ∗ ≈ 0.000989 . Вырожденный интервал конечного управления равен [0.0693, 1.4717].

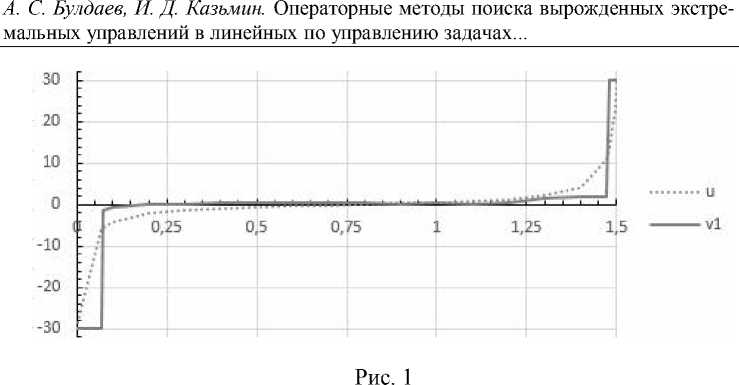
Операторный метод (17) .

Итерационный процесс (17) в поточечной форме при к > 0 имеет вид: ик+1(t) = и*(^(t, ик), x(t), t), t G T , где x(t), t g T является решением специальной фазовой задачи Коши, получающейся при замене переменной управления на выражение и*(у(t, ик), x(t), t) в правой части фазовой системы.

Для адекватного сравнения эффективности результатов итерационного процесса (17) с результатами, полученными в [7], равенство нулю функции переключения g 1 ( x ) = g ( ^ ( t , и^к ), x ) на итерационных приближениях также оценивалась с точностью e v = 10 ^-3 . В этом случае значение управления и^{к + 1}( t ) на вырожденном интервале определялось по правилу дифференцирования тождества g 1 ( x ( t , и )) ^ 0 и вычисления вырожденного управления и ( t ) в силу фазовой системы.

На рисунке 2 представлено конечное расчетное управление v 2( t ), t g T , полученное методом (17) с указанного выше начального управления и ( t ) с количеством итераций улучшения, равным 24, и значением функционала Ф * ® 0.000552 . Вырожденный интервал конечного управления равен [0.0857, 1.4463].

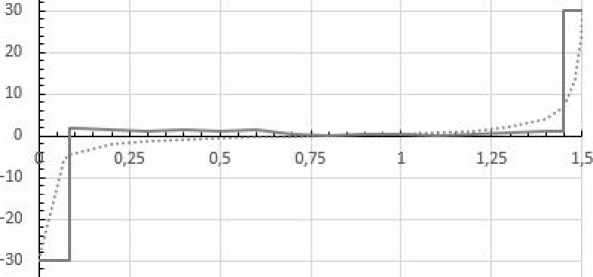
Рис. 2

Проекционный операторный метод (19).

Для заданного a >  0 итерационный процесс (19) в поточечной форме при k >  0 принимает вид:

u^{k + 1} ( t ) = P U ( u^k ( t ) + ag(у(t , u^k ), x ( t , u^k ))), t e T.

На рисунке 3 представлено конечное расчетное управление v 3( t ), t e T , полученное методом (19) с указанного выше начального управления u ( t ) при a = 10 ^{- 2} с количеством итераций улучшения, равным 14, и значением функционала Ф * ® 0.001421 . Вырожденный интервал конечного управления в смысле функции g(у, x ) равен [0.0698, 1.4609].

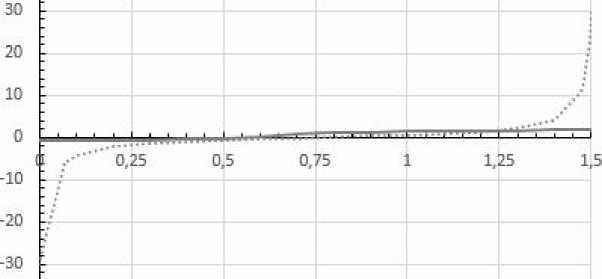
Рис. 3

Проекционный операторный метод (20).

Для заданного a >  0 итерационный процесс (20) в поточечной форме при k >  0 принимает вид:

uk+1(t) = Pu (uk (t) + ag(у(t,uk),x(t))), t g T, где x(t), t g T является решением специальной фазовой задачи Коши, получающейся при замене переменной управления на выражение PU (uk (t) + ag(у(t,uk),x(t))) в правой части фазовой системы.

На рисунке 4 представлено конечное расчетное управление v 4( t ), t g T , полученное методом (20) с указанного выше начального управления u ( t ) при a = 10 ^{- 2} с количеством итераций улучшения, равным 26, и значением функционала Ф * ® 0.000704 . Вырожденный интервал конечного управления в смысле функции g ₁( x ) равен [0.0751, 1.4512].

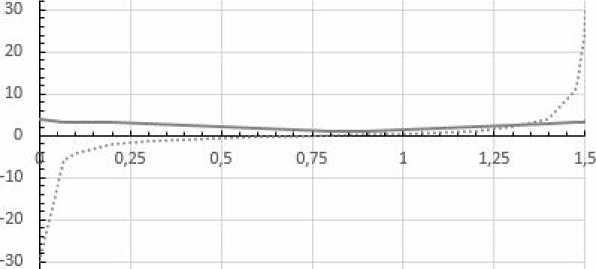
Рис. 4

Проекционный операторный метод (21) .

Для заданного a >  0 итерационный процесс (21) в поточечной форме при k >  0 принимает вид:

uk+1(t) = Pu (uk (t) + ag(у(t),x(t,uk))), t G T, где у(t), t g T является решением специальной сопряженной задачи Коши, получающейся при замене переменной управления на выражение PU(uk(t) + ag(у(t),x(t,uk))) в правой части сопряженной системы и переменной x(t1) на выражение x(t1, uk) в правой части начального условия в момент времени t1 .

На рисунке 5 представлено конечное расчетное управление v 5( t ), t g T , полученное методом (21) с указанного выше начального управления u ( t ), c a = 10 ^{- 2} и с количеством итераций улучшения, равным 17, и значением функционала Ф * ® 0.000676 . Вырожденный интервал конечного управления в смысле функции переключения g ₂( V ) = g(V,x ( t , u k )) равен [0.0799, 1.4485].

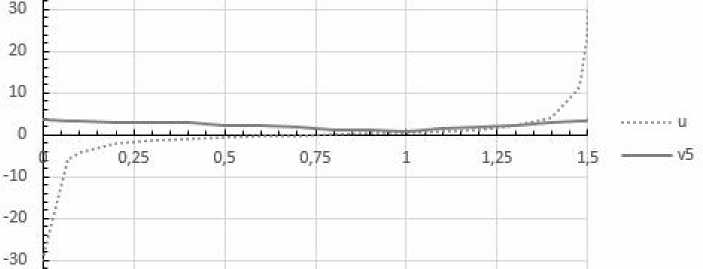
Рис. 5

Комбинированный операторный метод

В отличие от оптимального управления расчетные приближения экстремального управления, полученные проекционными операторными методами, не принимают граничных значений управления вне интервалов вырожденности управления. Поэтому указанные расчетные приближения в целях лучшего приближения к оптимальному управлению можно уточнять операторными методами на основе операции максимизации, позволяющими получать граничные значения управления вне интервалов вырожденности.

На рисунке 6 представлено конечное расчетное управление v 6( t ), t g T , полученное методом (17) с указанного выше расчетного управления v 5( t ), t g T , полученного проекционным методом (21), при a = 10 ^{- 2} с количеством итераций улучшения, равным 3, и значением функционала Ф * ® 0.000598 . Вырожденный интервал конечного управления равен [0.0799, 1.4485].

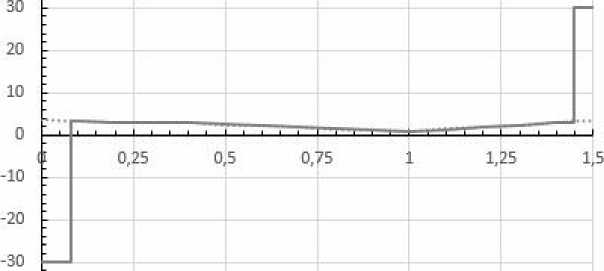
Рис. 6

В результате получаем, что вырожденные интервалы расчетных управлений v 5 и v 6 совпадают и на вырожденном интервале уточненное расчетное управление v 6 практически не отличается от расчетного приближения v 5 экстремального управления, полученного проекционным методом.

Проведенные расчеты в рамках модельной задачи показывают высокую эффективность рассматриваемых операторных методов принципа максимума для поиска вырожденных экстремальных управлений, позволяющих получать лучшие значения критерия оптимальности по сравнению с известным глобальным методом Кротова. При этом существенно более простой в вычислительной реализации проекционный операторный метод по сравнению с операторным методом на основе операции максимизации позволяет достаточно точно рассчитывать вырожденные интервалы экстремальных управлений.

Заключение

В классе нелинейных задач оптимального управления на основе рассматриваемых операторных форм принципа максимума рассмотрены модельно-ориентированные итерационные алгоритмы, позволяющие находить вырожденные экстремальные управления.

Разработанные операторные методы поиска вырожденных экстремальных управлений характеризуются следующими свойствами:

• 1)    нелокальность последовательных приближений управления на каждой итерации, получаемых расчетом двух задач Коши для фазовых и сопряженных переменных;

• 2)    численное решение задач Коши без определения специальных вспомогательных функций переключения Кротова на каждой итерации в отличие от известного глобального метода Кротова ;

• 3)    вычислительная устойчивость, которой не обладают стандартные методы решения краевой задачи принципа максимума;

• 4)    отсутствие трудоемкой процедуры игольчатого или выпуклого варьирования управления в малой окрестности рассматриваемого приближения, свойственной градиентным методам.

Указанные свойства предлагаемых операторных методов являются важными для повышения эффективности поиска вырожденных экстремальных управлений в рассматриваемом классе линейных по управлению задач оптимального управления.