Операторные уравнения и алгоритмы принципа максимума в задачах оптимального управления

Известный подход для решения задач оптимального управления состоит в построении и решении систем необходимых условий оптимальности управления. В частности, строят и решают краевую задачу принципа максимума [1; 2]. Другим распространенным подходом является построение релаксационных последовательностей управления на основе последовательного решения задач локального улучшения управления. При определенных условиях такие последовательности сходятся к экстремальным управлениям (удовлетворяющим необходимым условиям оптимальности). Пример такого подхода представляют известные градиентные методы [1–3].

В статье рассматривается новый подход к поиску экстремальных управлений, состоящий в построении необходимых условий оптимальности управления в форме операторных уравнений, интерпретируемых как задачи о неподвижной точке. Такая форма позволяет применить и адаптировать известные в вычислительной математике теорию и алгоритмы [4] для поиска неподвижных точек конструируемых операторных уравнений. Операторный подход неподвижных точек иллюстрируется в рамках класса задач оптимального управления со свободным правым концом. В работах [5-7] были предложены задачи и методы неподвижных точек принципа максимума на основе операции на максимум функции Понтрягина. В данной работе рассматриваемый подход неподвижных точек дополняется операторными уравнениями принципа максимума на основе операции проектирования и анализом сходимости проекционных итерационных процессов.

1 Задача оптимального управления со свободным правым концом Рассматривается задача оптимального управления:

Ф ( и ) = ф (x ( t j )) + [ F ( x ( t ), и ( t ), t ) dt ^ inf,            (1)

T                            u ∈ V

x ( t ) = f ( x ( t ), и ( t ), t ), x ( t 0 ) = x ⁰, и ( t ) g U , t g T = [ 1 0 , 1 1 ], (2) в которой x ( t ) = ( x 1 ( t ),..., x n ( t )) — состояние системы, и ( t ) = ( u 1 ( t ),..., u m ( t )) — управление. Множество допустимых управлений состоит из кусочнонепрерывных функций, принимающих значения в выпуклом компактном множестве U с R m :

V = { v g PC ( T ): v ( t ) g U , t G T } .

Начальное состояние x ⁰ и интервал времени T заданы.

Используется следующая система обозначений: qx — частная производная первого порядка функции q по соответствующему аргумен- n ту x; (х, у^ = ^xy — скалярное произведение векторов x, у в i=1

евклидовом пространстве E n ; || x || — норма вектора x в евклидовом пространстве.

Предполагается, что функция ф ( x ) непрерывно дифференцируема на R n ; функции F ( x , и , t ), f ( x , и , t ) и их производные F_x ( x , и , t ), F u ( x , и , t ), f_x ( x , и , t ), f_M ( x , и , t ) непрерывны по совокупности аргументов на множестве R n х U х T ; функция f ( x , и , t ) удовлетворяет условию Липшица по x в R n х U х T с константой L >  0 :

II ^{f ( x} , ^и , t ) ^{- f (} у , ^и , t )|| <  L ||x ^- у || .

Рассмотрим функцию Понтрягина с сопряженной переменной ψ ∈ Rⁿ

H ( ^ , x , и , t ) = ( f ( x , и , t ), ^ ) - F ( x , и , t ).

Стандартная сопряженная система имеет вид:

^у ( t ) = ^{- H} x ⁽ у ⁽ t ), ^x ( t ), ^{u (} t ), t ) ,       у ⁽ t 1 ) = Ф ^{( x} ( t D).

Для допустимого управления v e V обозначим x ( t , v ), t e T — решение системы (2); у ( t , v ), t e T — решение сопряженной системы при u ( t ) = v ( t ), x ( t ) = x ( t , v ), t e T .

С помощью отображения

u* (у, x, t) = argmax H(у, x, w, t), у e Rn, x e Rn, t e T (3) w∈U известное необходимое условие оптимальности управления v∈V (принцип максимума) [1-3] можно представить в следующей форме:

v(t) = u* (у(t,v),x(t,v),t), t e T.(4)

Соотношение (4) на множестве допустимых управлений является эквивалентным краевой задаче принципа максимума в пространстве состояний:

x( t) = f (x (t), u * (у( t), x (t), t), t),    x (to) = x °,(5)

у(t) = -Hx (у(t),x(t),u* (у(t),x(t),t),t), у(tr) = -Фx(x(t1)).

Эквивалентность понимается в следующем смысле.

Пусть пара ( x ( t ), у ( t )), t e T является решением краевой задачи (5), (6). Тогда формируемое по правилу (3) выходное управление v ( t ) = u * ( у ( t ), x ( t ), t ) удовлетворяет условию (4). Обратно, пусть управление v e V является решением задачи (4). Тогда формируемая пара функций ( x ( t , v ), у ( t , v )), t e T в силу их определения удовлетворяет краевой задаче (5), (6).

В общем случае правые части краевой задачи (5), (6) разрывны и многозначны по фазовым переменным x , у .

Из принципа максимума (4) следует ослабленное необходимое условие оптимальности, известное как дифференциальный принцип максимума [2; 3], который в форме неравенства имеет вид:

{H u ( у (t , u ), x ( t , u ), u ( t ), t ), w - u ( t )) <  0, w e U , t e T .         (7)

Введем отображение wa , a > 0 с помощью соотношения wa (у, x, u,t) = PU (u + aHu (у,x, u, t)), у e Rn, x e Rn, u e U, t e T, где PU — оператор проектирования на множество U в евклидовой норме

P u ( z ) = arg min(|| w - z ||),     z e R m .

w ∈ U

На основании условия Липшица для оператора PU функция wa непрерывна по совокупности (у,x,u,t) e Rn x Rn x U x T . При этом имеет место неравенство

(H u ( у , x , u , t ), w ^a ( у , x , u ,

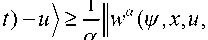
t ) ^- u ||².

Указанная оценка обеспечивается свойствами операции проектирования.

Дифференциальный принцип максимума (7) для управления u е V с помощью отображения w ^a можно записать в следующей форме:

u ( t ) = w a ( v (t , u ), x ( t , u ), u ( t ), t ), t e T , a >  0.

Отметим, что для выполнения (7) достаточно проверить условие (8) хотя бы для одного a >  0. Обратно, из условия (7) следует выполнение (8) для всех a >  0.

Условие (8) можно представить в форме эквивалентной дифференциально-алгебраической краевой задачи дифференциального принципа максимума:

x ( t ) = f ( x ( t ), u ( t ), t ), x ( 1 0) = x ° , ^{v (} t ) = - H x ⁽ v ⁽ t ), ^{x (} t ), u ⁽ t ), t ), v ⁽ t j = ф ^{( x (} t D), u ( t ) = w ^a ( v ( t ), x ( t ), u ( t ), t ), t e T .

Выделим важный для приложений подкласс линейных по управлению задач (функции f ( x , u , t ), F ( x , u , t ) линейны по u ), представляемый в виде:

Ф ( u ) = ф ( x ( t 1 )) + j^ (( a ( x ( t ), t ), u ( t )) + d ( x ( t ), t )) dt ^ inf, (9)

ueV

x ( t ) = A ( x ( t ), t ) u ( t ) + b ( x ( t ), t ), x ( 1 ₀) = x ⁰, u ( t ) e U , t e T . (10)

В задаче (9), (10) функция Понтрягина имеет следующую структуру

H( v ,x , u , t ) = H o ( v , x , t ) + ( H , ( v , x , t ), u ),

H o ( v , x , t ) = V , b ( x , t )} - d ( x , t ), H i ( v , x , t ) = A T ( x , t ) v — a ( x , t ). Отображение u * представляется в форме

u * ( v , x , t ) = arg max ( H , ( v , x , t ), w \.

weU

В частности, для скалярного управления ( m = 1) с областью значений U = [ u - , u ⁺ ] (двусторонние ограничения) имеем:

u -, H 1(v, x, t) < 0, u * (v, x, t) = <

u ⁺ , H 1 ( v , x , t ) >  0, w e U , H 1 ( v , x , t ) = 0.

При этом если U = [ - 1 , l ], то отображение u * можно представить в форме u * ( v , x , t ) = 1 • sign ( g ( v , x , t )), в которой значение

'-1, g(v, x, t) < 0, +1, g(v, x, t) > 0, sign (v, x, t) = <

, w e [ - 1,1], g ( v , x , t ) = 0

определяется знаком функции переключения g ( v , x , t ) = H 1 ( v , x , t ).

В задаче (9), (10) дифференциальный принцип максимума (7) является эквивалентным принципу максимума (4). Таким образом, в линейной по управлению задаче для поиска экстремальных управлений, удовлетворяющих принципу максимума, можно использовать проекционную форму

• (8)    дифференциального принципа максимума, которая проще по свойствам гладкости, чем условие принципа максимума (4).

Трудности решения краевой задачи принципа максимума (5), (6) известными методами (метод стрельбы, метод линеаризации, конечноразностный метод), в том числе и в случае гладкости и однозначности правых частей краевой задачи, связаны с вычислительной неустойчивостью методов, обусловленной наличием положительных вещественных значений собственных чисел соответствующей матрицы Якоби.

В данной работе развивается подход [5-7] к поиску экстремальных управлений, основанный на переходе от решения краевых задач принципа максимума в пространстве состояний к решению эквивалентных операторных уравнений принципа максимума в пространстве управлений, рассматриваемых как задачи о неподвижной точке конструируемых операторов управления.

• 2 Операторные уравнения на основе операции на максимум

Условие принципа максимума (4) с помощью применяемой системы обозначений решений фазовой и сопряженной систем в форме зависимости от управления можно интерпретировать как задачу о неподвижной точке некоторого оператора управления:

v = G ^ ( v ), v g V .

Оператор G , можно формализовать в виде суперпозиции трех отображений.

Первое отображение X определим с помощью соотношения

X ( v ) = x , v G V , x ( t ) = x ( t , v ), t G T .

Второе отображение V сконструируем аналогичным образом:

V ( v ) = у , v G V , у ( t ) = у ( t , v ), t G T .

Третье отображение V ∗ построим в виде

V * ( у , x ) = v * , у G C (T ), x G C ( T ), v * ( t ) = u * ( у ( t ), x ( t ), t ), t G T , где C ( T ) — пространство непрерывных на T функций.

В результате задачу (4) можно представить как операторное уравнение в пространстве управлений:

v = V * ( V ( v ), X ( v )), v G V .                     (11)

Уравнение (11) можно записать в канонической форме задачи о неподвижной точке с оператором G ^ , определяемым в виде суперпозиции:

G ( v ) = V * ( V ( v ), X ( v )).

Построим новые операторные задачи о неподвижной точке, эквивалентные краевой задаче принципа максимума (5), (6) и условию (4).

Введем отображение X * следующим образом:

X * ( у ) = x , у G C (T ), x G C ( T ), где x ( t ), t g T является решением специальной задачи Коши

i( t ) = f ( x ( t ), u * ( у ( t ), x ( t ), t ), t ), x ( 1 0 ) = x ⁰.

Рассмотрим операторное уравнение v = V* (T(v), X* (T(v))), v g V.                (12)

Покажем, что уравнение (12) эквивалентно уравнению (11).

Действительно, пусть v g V является решением уравнения (11), т. е. пара ( x ( t , v ), у ( t , v )), t g T является решением краевой задачи (5), (6).

Тогда функция x ( t , v ), t g T является решением задачи Коши

*( t ) = f ( x ( t ), u * ( у ( t , v ), x ( t ), t ), t ), x ( 1 0 ) = x ⁰,

• т. е. X ( v ) = X * ( T ( v )).

Отсюда получаем, что

V * ( T ( v ), X * ( T ( v ))) = V * ( T ( v ), X ( v )) = v .

Обратно, пусть v g V является решением уравнения (12), т. е.

v (t) = u * (у( t, v), x (t), t), где x(t), t g T является решением специальной задачи Коши

x ( t ) = f ( x ( t ), u * ( у ( t , v ), x ( t ), t ), t ), x ( 1 0 ) = x ⁰.

Следовательно, x ( t ) = x ( t , v ), t g T , т.е. X * ( T ( v )) = X ( v ).

Таким образом получаем:

V * ( T ( v ), X ( v )) = V * ( T ( v ), X * ( T ( v ))) = v .

Рассмотрим оператор управления G 2 в форме суперпозиции отображений:

G * ( v ) = V * ( T ( v ), X * ( T ( v ))).

Тогда операторное уравнение (12) представляется в форме канонической задачи о неподвижной точке:

v = G 2 ( v ), v g V .

В поточечной форме задачу (12) можно записать в виде:

v ( t ) = u * ( ^ ( t , v ), x ( t , V * ( T ( v ), X * ( T ( v )))), t ), t G T .

Еще одну операторную задачу о неподвижной точке, эквивалентную краевой задаче принципа максимума и условию (4), получаем с помощью следующего отображения:

T * ( x ) = у , x G C ( T ), _V G C ( T ), в котором у ( t ), t g T является решением специальной сопряженной задачи Коши

^{у (} t ) = - H x⁽ у ⁽ t ), ^{x (} t ), ^u * ⁽ у ⁽ t ), ^{x (} t ), t ), t ), у ⁽ t 1 ) = -Фх ^{( x (} t 1 )).

Рассмотрим операторное уравнение v = V* (T* (X(v)),X(v)), v g V.                (13)

Аналогично проведенному рассуждению можно показать эквивалентность уравнений (13) и (11).

Построим оператор управления G ₃ * по формуле:

G * ( v ) = V * ( V * ( X ( v )), X ( v )).

Тогда уравнение (13) представляется в канонической форме задачи о неподвижной точке v = G3* (v), v g V.

В поточечной форме задача (13) записывается в виде:

v ( t ) = u * ( у ( t , V * ( V * ( X ( v )), X ( v ))), x ( t , v ), t ), t g T .

Операторные формы задач о неподвижной точке на основе операции на максимум (11), (12), (13) являются основой для конструирования численных методов поиска экстремальных управлений.

• 3    Операторные уравнения на основе операции проектирования

Условие дифференциального принципа максимума в проекционной форме (8) можно представить в виде эквивалентных операторных уравнений на множестве допустимых управлений, интерпретируемых как задачи о неподвижной точке.

Введем вспомогательный оператор V a , a >  0 соотношением

Va (v, x, v) = va ,      у G C (T), x G C (T), v G V, va (t) = wa (v(t),x(t),v(t),t) = Pu(v(t) + aHu (v(t),x(t),v(t),t)), t g T. Определим оператор Xa , a > 0:

X ^a ( у , v ) = x ^a , V G C ( T ), v G V , x ^a ( t ) = x ^a ( t у ,v ), t G T , где x ^a ( t , v , v ), t g T — решение задачи Коши:

i( t ) = f ( x ( t ), w ^a ( у ( t ), x ( t ), v ( t ), t ), t ), x ( 1 0 ) = x ⁰.

Построим оператор V ^a , a >  0:

V ^a ( x , v ) = V^a , x G C ( T ), v G V , V^a ( t ) = V^a ( t , x , v ), где v^a ( t , x , v ), t g T — решение сопряженной задачи Коши:

^{V (} t ) = ^- H x ⁽ V ⁽ t ), ^{x (} t ), w ^{a (} V ⁽ t ), ^{x (} t ), ^{v (} t ), t ), t ), V ⁽ t 1 ) = -Фх ^{( x (} t 1 )).

На основе введенных ранее отображений V : u ^ v ( t , u ), t g T и X : u ^ x ( t , u ), t g T сконструируем операторы G a , G a , G a в форме: G a ( v ) = V ^a ( V ( v ), X ( v ), v ), v G V , G a ( v ) = V ^a ( V ( v ), X ^a ( V ( v ), v ), v ), v g V , G a ( v ) = V ^a ( V ^a ( X ( v ), v ), X ( v ), v ), v G V .

Рассмотрим три операторных уравнения в виде задач о неподвижной точке v = Va (V(v), X(v), v) = Ga (v), v g V, a > 0,(14)

v = Va (V(v), Xa (V(v), v), v) = Ga (v), v g V, a > 0,(15)

v = Va (Va (X(v), v), X(v), v) = Ga3 (v), v g V, a > 0.(16)

Эквивалентность задач (14), (15), (16) и условия дифференциального принципа максимума (8) показываются аналогично предыдущему разделу.

Выделим следующие важные особенности проекционных операторных уравнений. Конструируемые проекционные операторы управления в силу свойств операции проектирования являются непрерывными и удовлетворяют условию Липшица в отличие от разрывных и многозначных в общем случае операторов управления на основе операции на максимум.

Экстремальные управления, интерпретируемые как неподвижные точки операторных проекционных задач (14-16), могут определяться при любом значении параметра проектирования a >  0, в том числе при достаточно малом значении.

Указанные особенности являются существенными факторами повышения эффективности численного поиска экстремальных управлений на основе проекционных операторных уравнений.

• 4    Итерационные алгоритмы на основе операции на максимум

Рассмотрим задачу о неподвижной точке v = G(v), vеVe,                         (17)

в которой G : V _E ^ V _E является оператором, действующим на множестве V _E в полном нормированном пространстве E с нормой ||-||_Е .

Для численного решения задачи (17) можно использовать известный в вычислительной математике метод последовательных приближений и его модификации [4]. В частности, метод простой итерации при к >  0, имеющий вид:

v k ^{+ 1} = G ( v^k ), v ⁰ е V e .                             (18)

Для того чтобы улучшить сходимость итерационного процесса метода последовательных приближений, задача (17) может быть преобразована к эквивалентной задаче о неподвижной точке с параметром 5 е R :

v = v + 5 ( v - G ( v )), v е V _E , 5 * 0 .

Метод простой итерации для преобразованной задачи принимает вид:

v^{k + 1} = v^k + 5 ( v^k - G ( v^k )), v ⁰ е V _E , 5 * 0.

Выбором параметра 5 * 0 можно регулировать сходимость указанной модификации метода простой итерации.

Задачи о неподвижной точке принципа максимума (11), (12), (13) являются основой для соответствующих методов простой итерации при к >  0:

v^{k + 1} = V * ( Т ( v^k ), X ( v^k )), v ⁰ е V , v^{k + 1} = V * ( Y ( v^k ), X * ( Y ( v^k ))), v ⁰ е V , v^{k + 1} = V * ( Y * ( X ( v^k )), X ( v^k )), v ⁰ е V .

В поточечной форме первый метод имеет вид:

v^{k + 1}( t ) = u * И t , v^k ), x ( t , v^k ), t ), v ⁰ е V , t е T .          (19)

В соответствии с определением отображений имеет место следующее соотношение:

X(V * ( V ( v ), X * ( V ( v )))) = X * ( V ( v )), v е V .          (20)

Действительно, для любого p е C(T ) по определению получаем:

X* (p)|t = х(t), t е T, где х(t), t е T является решением задачи Коши:

х ( t ) = f ( х ( t ), u * ( p ( t ), х ( t ), t ), t ), х ( t 0 ) = х ⁰.

Далее, согласно определению имеем:

V*(Р, X*(Р))|t = u *(Р(t),х(t), t), t е T, где х(t), t е T является решением задачи Коши:

х ( t ) = f ( х ( t ), u * ( p ( t ), х ( t ), t ), t ), х ( t 0 ) = х ⁰.

Следовательно,

х ( t ) = X * ( V * ( p , X * ( p )))| t , t е T .

Таким образом, из поточечных равенств получаем операторное равен -ство:

X(V * ( p , X * ( p ))) = X * ( p ), p е C ( T ), из которого следует (20).

Согласно итерационному процессу из (20) следует:

X * ( V ( v k )) = X (V * ( V ( v k ), X * ( V ( v k )))) = X ( v k ^{+ 1}).

Следовательно, второй метод простой итерации представляется в следующем неявном виде:

v k ^{+ 1} = V * ( V ( v k ), X ( v k ^{+ 1})), v ⁰ е V , или в поточечной форме:

v k ^{+ 1}( t ) = u * ( ^ ( t , v k ), х ( t , v k ^{+ 1}), t ), v ⁰ е V , t е T .         (21)

Аналогично из определения рассматриваемых отображений следует выполнение следующего соотношения:

V ( V * ( V * ( X ( v )), X ( v ))) = V * ( X ( v )), v е V .          (22)

Отсюда получаем:

V * ( X ( v k )) = V ( V * ( V * ( X ( v k )), X ( v k ))) = V ( v k ^{+ 1}).

В итоге, третий метод простой итерации принимает следующий неявный вид:

v k ^{+ 1} = V * ( V ( v k ^{+ 1}), X ( v k )), v ⁰ е V , или в поточечной форме:

v k ^{+ 1}( t ) = u * ( ^ ( t , v k ^{+ 1}), х ( t , v k ), t ), v ⁰ е V , t е T .         (23)

Для оценки вычислительной эффективности итерационных алгоритмов важно отметить, что трудоемкость реализации одной итерации неявных методов (21), (23) аналогична трудоемкости реализации явного метода (19) и составляет две задачи Коши для фазовых и сопряженных переменных.

Действительно, на к -й итерации при к >  0 процесса (21) после вычисления решения задачи Коши у ( t , v^k ), t e T находится решение x ( t ), t e T фазовой системы:

x(t ) = f ( x ( t ), u * ( у ( t , v^k ), x ( t ), t ), t ), x ( t o ) = x ⁰.

Затем строится выходное управление по правилу:

v^{k + 1}( t ) = u * ( у ( t , v^k ), x ( t ), t ), t e T .

При этом в силу построения выполняется соотношение:

x ( t ) = x ( t , v^{k + 1}), t e T .

Аналогично, на к -й итерации процесса (23) после вычисления x ( t , v^k ), t e T находится решение у ( t ), t e T сопряженной системы:

у ( t ) = - H x ( у ( t ), x ( t , v^k ), u * ( у ( t ), x ( t , v^k ), t ), t ), у ( t i ) = - y x ( x ( t i , v^k )).

Затем строится выходное управление по правилу:

v^{k + 1}( t ) = u * ( у ( t ), x ( t , v^k ), t ), t e T , для которого по построению выполняется соотношение:

у ( t ) = у ( t , v^{k + 1}), t e T .

Отметим, что только на начальной итерации процесса (21) при k = 0 для вычисления у ( t , v ⁰), t e T требуется решить дополнительную задачу Коши, чтобы получить решение x ( t , v ⁰), t e T .

Сравнивая предлагаемые алгоритмы с другими известными итерационными методами принципа максимума, отметим, что явный метод (19) совпадает с простейшим методом последовательных приближений [8] для решения уравнения (4). Известных аналогов неявных итерационных методов неподвижных точек (21) и (23) в литературе не найдено.

Для сравнительного выделения характерных особенностей предлагаемых операторных методов неподвижных точек (19), (21), (23) рассмотрим структуру двух распространенных известных методов принципа максимума в используемых обозначениях.

Стандартный метод условного градиента [2; 3] для решения (4) описывается соотношениями:

v^k ( t ) = u * ( у ( t , v^k ), x ( t , v^k ), t ), t e T , v ⁰ e V , k >  0, v ^k ( t ) = v^k ( t ) + Л ( v^k ( t ) - v^k ( t )), t e T ,

A e [0,1]: Ф ( v ^k ) <Ф ( v^k ) ^ v^{k + 1}( t ) = v ^k ( t ), t e T .

Метод игольчатой линеаризации [3] для решения уравнения (4) характеризуется соотношениями:

vk(t) = u*(у(t,vk),x(t,vk),t), t e T, v0 e V, k > 0, gk(t) = AvkH(у1(t, vk),x1(t,vk), vk(t),t), t e T, Amin = inf gk (t) , Anax = SUP gk (t) , t∈T                         t∈T vX( t) =

; v k ( t ), g ( t ) <  x ,

X e [ X _mm, X _max], t e T ,

\ v^k ( t ), g^k ( t ) >  X ,

X e [ X _mm, X _max]: Ф ( v X ) <Ф ( v^k ) ^ v^{k + 1}( t ) = v X ( t ), t e T .

Характерным для указанных известных методов является поиск первого приближения v^k управления, которое затем варьируется в окрестности улучшаемого управления v^k с целью улучшения по целевому функционалу задачи.

Таким образом, в предлагаемых операторных методах неподвижных точек, в отличие от известных градиентных методов и методов принципа максимума, не гарантируется релаксация по целевому функционалу на каждой итерации методов. Компенсируют свойство релаксации нелокальность последовательных приближений управления и отсутствие на каждой итерации достаточно трудоемкой операции выпуклого или игольчатого варьирования управления в окрестности текущего управления.

• 5    Итерационные алгоритмы на основе операции проектирования

Для решения операторных задач о неподвижной точке дифференциального принципа максимума (14), (15), (16) можно применить соответствующие методы простой итерации при k >  0, которые в операторной форме имеют вид:

vk+1 = Va (T(vk), X(vk), vk), v0 e V, a > 0, vk+1 = Va (T(vk), Xa (T(vk), vk), vk), v0 e V, a > 0, vk+1 = Va (Ta (X(vk), vk), X(vk), vk), v0 e V, a > 0.

Аналогично получению в предыдущем разделе соотношений (20) и (22) можно получить следующие операторные соотношения:

X(V ^a ( p , X ^a ( p , v ), v )) = X ^a ( p , v ), p e C(T ), v e V , T ( V ^a ( T ^a ( x , v ), x , v )) = T ^a ( x , v ), x e C ( T ), v e V . Отсюда имеем:

X ^a ( T ( v^k ), v^k ) = X(V ^a ( T ( v^k ), X ^a ( T ( v^k ), v^k ), v^k )) = X ( v^{k + 1}),

T ^a ( X ( v^k ), v^k ) = T ( V ^a ( T ^a ( X ( v^k ), v^k ), X ( v^k ), v^k )) = T ( v^{k + 1}).

Таким образом, второй и третий методы простой итерации для поиска неподвижных точек дифференциального принципа максимума можно записать в неявном виде:

vk+1 = Va (T(vk), X (vk+1), vk), v0 e V, a > 0, vk+1 = Va (T(vk+1), X(vk), vk), v0 e V, a > 0.

В поточечной форме итерационные методы дифференциального принципа максимума принимают вид:

vk+1( t) = wa И t, vk), x (t, vk), vk (t), t), v0 e V, a > 0, t e T,(24)

vk+1(t) = wa (^(t, vk),x(t, vk+1), vk(t), t), v0 e V, a > 0, t e T,(25)

vk+1( t) = wa И t, vk+1), x (t, vk), vk (t), t), v0 e V, a > 0, t e T.(26)

Трудоемкость вычислительной реализации одной итерации явных и неявных проекционных методов составляют две задачи Коши для фазовых и сопряженных переменных.

Известных аналогов проекционных итерационных методов неподвижных точек (24), (25) и (26) в литературе не найдено.

Для сравнения разработанных проекционных методов неподвижных точек представим в используемых обозначениях стандартный метод проекции градиента с a >  0 [2; 3]:

va (t) = wa Иt,vk),x(t,vk),vk(t),t), t e T, ae (0,»): Ф(vka) <Ф(vk) ^ vk+1 = vka .

На каждой итерации рассматриваемого метода проекции градиента проекционный параметр варьируется для обеспечения улучшения имеющегося управления.

В построенных проекционных методах неподвижных точек, в отличие от стандартного метода проекции градиента, параметр проектирования a >  0 фиксируется в итерационном процессе последовательных приближений управления. Таким образом, на каждой итерации предлагаемых методов релаксация по целевому функционалу не гарантируется, но это свойство компенсируется нелокальностью последовательных приближений управления, отсутствием операции варьирования управления в окрестности текущего приближения для обеспечения улучшения по функционалу задачи, возможностью получения экстремальных управлений при достаточно малых параметрах проектирования, обеспечивающих принципиальную сходимость итерационных процессов.

• 6    Условия сходимости итерационных процессов

Анализ сходимости построенных итерационных процессов можно осуществить на основе известного принципа сжимающих отображений. Операторный аналог известной теоремы [4] можно сформулировать следующим образом.

Теорема 1. Пусть оператор G : V E ^ V E , действующий на множестве V E в полном нормированном пространстве E с нормой ||-||_Е, удовлетворяет условию Липшица в шаре:

B(v 0,1) = {v e VE : I v — v cl |E < l, v0 e VE, l > 0} с константой 0 < M = M(v0,1) < 1:

||G ( v ) - G ( u )| < M |v - u |, v e B ( v 0 , 1 ), u e B ( v 0 , 1 ).        (27)

При этом выполняется условие:

||G ( v о ) - v ₀|^< (1 - M ) l.                           (28)

Тогда задача о неподвижной точке (17) имеет единственное решение v е B ( v ₀ , l ) и итерационный процесс (18) сходится к v в норме ||-||_Е для любого начального приближении v ⁰ е B ( v ₀ , l ). Для погрешности метода выполняется оценка:

II ^v k ^{- v} lL< ^Mk\V ⁰ - v L,     ^k ^⁰.

Доказательство теоремы несложно проводится по методике аналогично работе [4].

Следует отметить, что условие (28) вводится для того, чтобы обеспечить невыход итерационных приближений процесса (18) за пределы множества B ( v ₀ , l ), на котором выполняется условие Липшица (27).

В работах [5-7] рассмотрены условия сходимости для явных итерационных процессов (19), (24). Анализ сходимости предлагаемых неявных процессов можно провести аналогично.

В качестве примера сформируем с помощью теоремы 1 следующие условия сходимости явного (23) и неявных (24), (25) процессов к решению уравнения (8) на подмножестве непрерывных допустимых управлений:

VC = {v е C (T): v (t) е U, t е T} с V с нормой ||v||C = max||v(t)||, v е VC.

Пусть семейство фазовых траекторий системы (2) на множестве V является ограниченным:

x ( t , v ) е X , t е T , v е V ,                        (29)

где X с R n — выпуклое компактное множество.

Отметим, что достаточным условием ограниченности (29) может быть выполнение известной оценки [1; 3] с константой C >  0 :

II f ( x , u , t )|| <  C (|| x || + 1), x е R n , u е U , t е T .

Предположим дополнительно, что функции f ( x , u , t ), F ( x , u , t ), ф (x ) дважды непрерывно дифференцируемы по совокупности переменных на соответствующих множествах R n x U x T и R n .

При выполнении ограничения (29) на основе достаточного условия применительно к сопряженной системе с учетом ее линейности получаем условие ограниченности семейства траекторий сопряженной системы:

^ ( t , v ) е P ,      t е T , v е V ,                    (30)

где P с R n — выпуклое компактное множество.

При сделанных предположениях можно показать аналогично [2] , что операторы X , V удовлетворяют условию Липшица с константами С , >  0, C ₂ >  0:

|| X (v) - X (u )| С < С,| v - 4С , IIТ (V) -т u )| С < C2I v - 4с , v е VC, u е VC, v е VC, и е VC .

Используя условие Липшица для оператора проектирования P_U и условий ограниченности (29), (30), получаем:

||x ^- ( t , p , и ) - x ^- ( t , q , v )|| =

= I x ( t , V a ( p , X a ( p , и ), и )) - x ( t , V a ( q , X a ( q , v ), v ))|| <

• < M 1 J| V a ( p , X a ( p , и ), и )| t - V a ( q , X a ( q , v ), v )\_t\\dt <

T

• < M ₂ J| | u ( t ) - v ( t )|| dt +

+- M 2 J|| H u ( p ( t ), x a ( t , p , и ), и ( t ), t ) - H u ( q ( t ), x a ( t , q , v ), v ( t ), t )|| dt ,

T где t е T, и, v е VC, p, q е C(T), M 1 = const > 0, M2 = const > 0.

Аналогично получаем:

I y a ( t , x , и ) - y^- ( t , y , v )|| =

= I y ( t , V ^a ( Т a ( x , и ), x , и )) - y ( t , V a ( Т a ( y , v ), y , v )) || <

• < M 3 J| V ^a ( Т a ( x , и ), x , и )| t - V ^a ( Т a ( y , v ), y , v H\\dt <

• < m , ji u ( t ) - v ( t ) | dt +

+a M ₄ J|| H , ( y a ( t , x , и ), x ( t ), и ( t ), t ) - H u ( y a ( t , y , v ), y ( t ), v ( t ), t )|| dt ,

T где t е T, и, v е VC, x, y е C(T), M3 = const > 0, M4 = const > 0.

Отсюда нетрудно обосновать при достаточно малом a >  0 оценки:

II X ^a ( V ( и ), и ) - X a ( Ф ( v ), v )| С <  (li a / M ⁵1 u - v c ,

⁽i a,v Z₆)

II^Т - ( X ( и ), и ) ^Т - ( X ( v ), v )| С <  11± а ) М 1 | и - v ll c ,

⁽1 ^— M g )

где и е V C , v е V C , константы M i >  0 , i = 5,6,7,8.

Для оператора проектирования P_U на основе выполнения условия Липшица имеет место следующее неравенство:

||w ^{- (} p , ^x , ^и , t ) ^- w ^{- (} q , y , v , t H < ||^{( u - v} ) + ^{- ( H} u ⁽ p , ^x , ^u , t ) ^{- H} u ⁽ q , y , v , t ^Ц² <

< l| u - v ||² + 2 - ( u - v , H u ( p , x , и , t ) - H u ( q , y , v , t )) + ^{+ a 2} 1 l ^H u ⁽ p , ^x , ^u , t ) ^{- H} u ⁽ q , y , v , t )||²,

и , v е U , p , q е P , x , y е X , t е T .

Предположим, что в шаре B ( v ₀, l ) с V C радиусом l >  0 с центром в точке v ₀ е V C для вектор-функции H u ( у , x , u, t ) выполняется условие:

(и ( t ) - v ( t ), H u ( у (t, u ), x ( t, u ), u ( t ), t ) - H u ( у (t, v ), x ( t, v ), v ( t ), t ) ) <

• <- K 1 || u ( t ) - v ( t )||² , u , v е B ( v 0 , l ), t е T ,

где K j = const >  0.

Тогда на основе неравенства (31) при достаточно малом a >  0 можно получить оценку:

||Va ( V ( u ), X ( u ), u ) - V a ( V ( v ), X ( v ), v )|| C <  (1 - 2 a K j + a ² M ₉)² | u - v|| C , где M ₉ = const >  0, u , v е B ( v ₀, l ).

Аналогично предположим, что в шаре B ( v ₀, l ) с V C радиусом l >  0 с центром в точке v ₀ е V C для вектор-функции H_u ( у , x , u , t ) выполняется условие:

uu ( t ) - v ( t ), H u ( у ( t , u ), x ( t , V a ( V ( u ), X a ( V ( u ), u ), u )), u ( t ), t ) -

• - H u ( у ( t , v ), x ( t , V a ( V ( v ), X a ( V ( v ), v ), v )), v ( t ), t )) < - K 21 u ( t ) - v ( t )f,

• u , v е B ( v 0 , l ), t е T , где K ₂ = const >  0.

Тогда на основе неравенства (31) при достаточно малом a >  0 можно получить оценку:

||V ^a ( V ( u ), X a ( V ( u ), u ), u ) - V a ( V ( v ), X a ( V ( v ), v ), v ) || C <

< (1 - 2a K 2 + a2 M ю)21|u - v^C где M10 = const > 0, u,v е B(v0,l).

Также предположим, что в шаре B ( v ₀, l ) с V C радиусом l >  0 с центром в точке v ₀ е V C для вектор-функции H_u ( у , x , u , t ) выполняется условие:

uu ( t ) - v ( t ), H u ( у ( t , V a ( V a ( X ( u ), u ), X ( u ), u )), x ( t , u ), u ( t ), t ) -

• - H u ( у ( t , V a ( V a ( X ( v ), v ), X ( v ), v )), x ( t , v ), v ( t ), t )) < - K 31 u ( t ) - v ( t )f,

• u , v е B ( v 0 , l ), t е T , где K ₂ = const >  0.

Тогда на основе неравенства (31) при достаточно малом a >  0 можно получить оценку:

||V a ( V a ( X ( u ), u ), X ( u ), u ) - V a ( V a ( X ( v ), v ), X ( v ), v )| ^ <

• < (1 - 2 a K ₃ + a ² M _H)² \\u - v||_C

где M ₁₁ = const >  0, u , v е B ( v ₀, l ).

Таким образом, в сделанных предположениях при достаточно малых a >  0 операторы G a , G a , G а удовлетворяют условию Липшица с константой меньше единицы на множестве B ( v ₀, 1 ).

В силу определения при достаточно малых а >  0 операторы G ^ , G a , G а удовлетворяют условию (28) в норме ||-| C пространства непрерывных функций C ( T ) для любого v ₀ е V_C . Таким образом, при достаточно малых а >  0 итерационные приближения процессов (24), (25) и (26) остаются в пределах множества B ( v ₀, 1 ) для любого начального приближения ^{v 0 е} B ^{( v} 0 , ¹ ) .

В результате на основе теоремы 1 можно сформировать соответствующие утверждения о сходимости процессов (24), (25) и (26). В частности, следующее утверждение о сходимости явного итерационного процесса (24).

Теорема 2. Пусть

• 1)    семейство фазовых траекторий в задаче (1), (2) ограничено:

x ( t , и ) е X , t е T , и е V , где X с Rⁿ — выпуклое компактное множество;

• 2)    вектор-функция f ( x , и , t ), функции F ( x , и , t ), ф (x ) дважды непрерывно дифференцируемы по совокупности переменных на соответствующих множествах R n х U х T и Rⁿ ;

• 3)    для вектор-функции Н_и( у ,x , и , t ) в шаре B ( v ₀, 1 ) с V_C радиусом 1 >  0 с центром в точке v ₀ е V_C выполняется условие:

Uи ( t ) - v ( t ), H u ( у ( t , и ), x ( t , и ), и ( t ), t ) - H u ( у ( t , v ), x ( t , v ), v ( t ), t )} <  <- K\\u ( t ) - v ( t )||² , и , v е B ( v 0 , 1 ), t е T , где K = const >  0.

Тогда для достаточно малых параметрах проектирования а >  0 итерационный процесс (24) сходится в норме ||-| C к единственному решению v ^а е B ( v ₀, 1 ) уравнения (8) для любого начального приближения v ⁰ е B ( v ₀, 1 ) при к = 0 .

Утверждения о сходимости неявных итерационных процессов (25) и (26) формулируются аналогично.

Теорема 3. Пусть

• 1)    семейство фазовых траекторий в задаче (1), (2) ограничено:

• x ( t , и ) е X , t е T , и е V , где X с Rⁿ — выпуклое компактное множество;

• 2)    вектор-функция f ( x , и , t ), функции F ( x , и , t ), ф (x ) дважды непрерывно дифференцируемы по совокупности переменных на соответствующих множествах Rⁿ х U х T и Rⁿ ;

• 3)    для вектор-функции H_u( у ,x , и , t ) в шаре B ( v ₀, 1 ) с V_C радиусом 1 >  0 с центром в точке v ₀ е V_C выполняется условие:

Uu ( t ) - v ( t ), H_u ( y ( t , u ), x ( t , u ), u ( t ), t ) - H_u ( y ( t , v ), x( t , v ), v ( t ), t )} <

• <- K\\u ( t ) - v ( t )||² , u , v e B ( v o , l ), t e T , где K = const >  0, функция x ( t , u ), t e T — решение задачи Коши:

x ( t ) = f ( x ( t ), w a ( y (t , u ), x ( t ), u ( t ), t ), t ), x ( t o ) = x ⁰.

Тогда для достаточно малых параметрах проектирования a >  0 итерационный процесс (25) сходится в норме ||-|| C к единственному решению v ^a e B ( v ₀, l ) уравнения (8) для любого начального приближения v ⁰ e B ( v ₀, l ) при k = 0 .

Теорема 4. Пусть

• 1)    семейство фазовых траекторий в задаче (1), (2) ограничено:

x ( t , u ) e X , t e T , u e V , где X c R" — выпуклое компактное множество;

• 2)    вектор-функция f ( x , u , t ), функции F ( x , u , t ), ф (x ) дважды непрерывно дифференцируемы по совокупности переменных на соответствующих множествах R " x U x T и R " ;

• 3)    для вектор-функции H_u( y ,x , u , t ) в шаре B ( v ₀, l ) c V C радиусом l >  0 с центром в точке v ₀ e V C выполняется условие:

uu ( t ) - v ( t ), H u ( y ( t , u ), x ( t , u ), u ( t ), t ) - H u ( y ( t , v ), x ( t , v ), v ( t ), t )} <  <- K||u ( t ) - v ( t )||² , u , v e B ( v 0 , l ), t e T , где K = const >  0, функция y ( t , u ), t e T — решение задачи Коши:

y ( t ) = - H x ( y ( t ), x ( t , u ), w ^a ( y (t ), x ( t , u ), u ( t ), t ), t ), y ( t j ) = -ф_х ( x ( t j , u )).

Тогда для достаточно малых параметрах проектирования a >  0 итерационный процесс (26) сходится в норме ||-|| C к единственному решению v ^a e B ( v ₀, l ) уравнения (8) для любого начального приближения v ⁰ e B ( v ₀, l ) при k = 0 .

Следствие. Пусть в условиях теорем 2, 3, 4 центр v ₀ e V C шара B ( v ₀, l ) удовлетворяет уравнению (8). Тогда v ^a = v ₀.

В условиях теорем 2, 3, 4 итерационные процессы для непрерывных начальных приближений v ⁰ e B ( v ₀, l ) могут сходиться только к непрерывным экстремальным управлениям.

Результаты теорем 2, 3, 4 могут быть обобщены на более широкий класс измеримых функций:

V c Vl = {v e L „ (T): v (t) e U, t e T} с нормой ||v||m = ess sup ||v(t)||, v e VL. В этом случае появляется принципи-∞         t∈T альная возможность сходимости итерационных процессов к экстремальным управлениям в классе кусочно-непрерывных управлений.

Таким образом, при достаточно малых параметрах проектирования операторы процессов (24), (25) и (26) определяют последовательности итерационных приближений, однозначно определенных и непрерывно зависящих от параметра проектирования, которые обладают принципиальной сходимостью к экстремальному управлению, удовлетворяющему дифференциальному принципу максимума (8). Результаты сходимости итерационных процессов зависят от выбора начального приближения процессов. В частности, в случае не единственного решения уравнения (8) сходимость итерационных процессов к тому или иному экстремальному управлению определяется выбором начального приближения.

Заключение

Предложены новые операторные формы принципа максимума в виде задач о неподвижной точке в пространстве управлений, которые позволяют эффективно применить и модифицировать известный аппарат теории и методов неподвижных точек для конструирования итерационных алгоритмов поиска экстремальных управлений.

Разработанные итерационные операторные методы поиска экстремальных управлений характеризуются нелокальностью последовательных приближений управления, отсутствием трудоемкой процедуры игольчатого или выпуклого варьирования управления в малой окрестности рассматриваемого приближения, характерной для градиентных методов, наличием в проекционных методах одного основного настроечного проекционного параметра, регулирующего сходимость итерационного процесса. В целом трудоемкость каждой итерации предлагаемых алгоритмов последовательных приближений определяется последовательным решением двух задач Коши для фазовых и сопряженных переменных.

Указанные свойства предлагаемых методов поиска экстремальных управлений принципиально важны для повышения эффективности решения задач оптимального управления и определяют перспективное направление развития методов оптимизации нелинейных динамических систем.