Описание электромагнитного поля в плоском конденсаторе при высокочастотном нагреве длинномерных диэлектриков
Автор: Качанов А.Н., Коренков Д.А.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Технические науки
Статья в выпуске: 10, 2016 года.
Бесплатный доступ
В статье рассматриваются вопросы высо-кочастотного нагрева. Исследование посвя-щено неравномерности нагрева, главной при-чиной которой является волновой характер распределения электромагнитного поля в материале. Неравномерность повышается с увеличением частоты поля и габаритов ма-териала. Данная проблема особенно актуаль-на для высокочастотных аппаратов для сушки древесины, длина загрузки которых может достигать 8 м. Для демонстрации неравно-мерности производятся расчеты распределе-ния напряженности электрического поля на разных частотах. Задача рассматривается в одномерной постановке. В качестве диэлек-трика выбрана древесина. Вычисления осу-ществляются 3 способами математического описания волновых явлений. Первый способ основывается на системе уравнений Максвел-ла и после ряда преобразований приводится к косинусоидальному виду. Второй описывает распределение электромагнитного поля в многослойной среде. Последний способ пред-ложен авторами и включает волновое уравне-ние Гельмгольца и граничные условия сим-метрии на свободном конце конденсатора и третьего рода в точке подключения токопро-вода. Для проверки корректности каждой из рассмотренных математических моделей приводятся ранее полученные эксперимен-тальные данные распределения напряжения по длине электродов рабочего конденсатора. На основе анализа расчетных и эксперименталь-ных результатов делаются выводы, что пер-вый способ наименее точный. Это объясняет-ся пренебрежением коэффициента затухания, который для влажной древесины обладает существенной величиной. Второй способ бо-лее точный, но, так же как и первый, привно-сит дополнительную погрешность в узлах напряжения. Максимальное совпадение с экс-периментом обеспечивает предложенная ав-торами модель при различных соотношениях длины волны и длины загрузки.
Высокочастотный нагрев древесины, распределение электромагнитного поля, вакуумно-диэлектрическая сушка
Короткий адрес: https://sciup.org/14084506
IDR: 14084506 | УДК: 621.365.5:621.319.4
Текст научной статьи Описание электромагнитного поля в плоском конденсаторе при высокочастотном нагреве длинномерных диэлектриков
Введение . Высокочастотный (ВЧ) диэлектрический нагрев используется во множестве технологических процессов различных отраслей промышленности. Основные требования, предъявляемые к ВЧ нагревательным установкам, заключаются в обеспечении достаточной интенсивности и равномерности нагрева. Соблюдение данных требований зависит от правильного выбора частоты и мощности ВЧ-генератора. На этапе проектирования, чтобы определить оптимальные параметры генератора, часто прибегают к математическому моделированию процесса нагрева с использованием дифференциального уравнения теплопроводности Фурье с внутренними источниками теплоты [1-4]
дТ _ ~ ср — = V(X VT) + Q, (1) от где с - теплоемкость, Дж/(кг°С); р - плотность, кг/м3; т - время, с; X - теплопроводность, Вт/(м-°С); T - температура, °С; Q - удельная мощность внутренних источников теплоты, Вт/м3.
Вопрос об обеспечении равномерного нагрева наиболее существенен для процессов термической обработки длинномерных диэлектриков, например для ВЧ-сушки пиломатериалов. В этом случае точность моделирования сильно зависит от правильного задания закона распределения удельной мощности Q , пропорциональной квадрату напряженности электрического поля [1]. Как будет показано ниже, известные способы описания волнового характера распределения электромагнитного поля имеют ограничения и подходят только для приближенных расчётов.
Цель работы . Поиск более точного способа описания электромагнитного поля в процессах ВЧ-нагрева длинномерных диэлектриков.
Задачи : получить более точную математическую модель волнового распределения напряженности электрического поля и проверить её адекватность.
ВЧ-сушка пиломатериалов проводится в конвективно-диэлектрических и вакуумнодиэлектрических камерах, которые снабжаются генераторами, работающими на частотах 5,28 или 13,56 МГц, и предназначаются для сушки штабелей древесины длиной до 6,5 м [5]. В то же время длина волны вдоль волокон сосновых досок при температуре 20оС и влажности 10 % на частоте 13,56 МГц составляет 14 м [6], т.е. она всего в 2,15 раза больше длины материала. Поэтому ВЧ сушильные камеры являются ярким примером объектов с распределёнными параметрами.
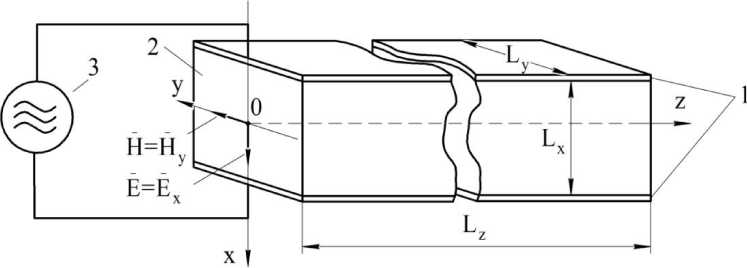
Рис. 1. Принцип установки для высокочастотного нагрева: 1 – электроды; 2 – материал; 3 – высокочастотный генератор
В отмеченных камерах электроды образуют со штабелем плоскопараллельный конденсатор, причём его длина Lz обычно в 5–6 раз превосходит остальные габариты Lx и Ly. Система координат приведена на рисунке 1. Описание электромагнитного поля осуществляется с помощью уравнений Максвелла, которые после ряда преобразований сводятся к волновым уравнениям Фредгольма для векторов напряженности электрического E и магнитного H полей [4]. Ввиду малости высоты и ширины штабеля по сравнению с длиной волны изменениями векторов E и H вдоль осей oy и ox пренебрегаем. Тогда уравнения Фредгольма могут быть упрощены до одноразмерной фор- мы:
∂ 2 E x - k 2 E = 0 , ∂ z 2 x
∂2H ∂z2y-k2Hy=0, где – k волновой коэффициент, 1/м; k(z)=j⋅2π⋅ f 4 ε0μ0ε(1 - j ⋅ tgδ)
= α+j ⋅ β ,
где μ – магнитная постоянные, Гн/м; α – коэффициент затухания, 1/м; β – коэффициент фазы, 1/м.
Аналитическое решение уравнения (2) приведено в [7] для среды с постоянными свойствами и допущением об отсутствии затухания волн (α= 0). После ряда преобразований оно записывается в виде
E x ( z ) = E max cos(β(L z - z )) , (4) где E – максимальное значение напряженности электрического поля (В/м), наблюдаемое на крае электродов, противоположном точке подключения генератора.
Такое упрощенное описание не может быть использовано при моделировании процессов диэлектрического нагрева по ряду причин. Во-первых, многие материалы, в том числе и влажная древесина, обладают существенным коэффициентом α, и дополнительным источником неравномерности нагрева является затухание электромагнитных волн. Во-вторых, диэлектрические свойства многих материалов зависят от температуры, а в случае древесины – ещё и от влажности. Поэтому в процессе сушки волновой коэффициент оказывается непостоянным как в пространстве, так и во времени.
В зарубежной литературе можно найти способ описания волнового характера распределения поля при неоднородном коэффициенте распространения, который используется при моделировании микроволнового нагрева. Согласно [8], исследуемый объект разбивают на участки. В пределах каждого из них диэлектрические свойства усредняются, и определяется волновой коэффициент k . Для i-го участка распределение напряженности электрического поля находят по закону
E ( z ) = A ( e -j-k ■ ■ z ■ + Rii+1e - j‘( k ■ • z ' - 2 k ' i A ) ) ; (5)
i• A Формулы для вычисления коэффициентов A и R приведены в указанном источнике. В работе [9] данный способ был применен для вычисления поля в конденсаторе при высокочастотной сушке древесины. Ниже произведён сравнительный анализ результатов и сделаны выводы об ограничениях его использования. Также в литературе, например [3, 10], встречается способ, заключающийся в непосред- ственном численном решении волнового уравнения (2), которое с учетом неоднородности диэлектрических свойств записывается в виде dE - k 2( z) Ex = 0. dz Решение может быть легко получено методом конечных разностей, однако основной вопрос возникает при выборе граничных условий. В [10] при моделировании процесса СВЧ- нагрева на конце загрузки со стороны излучателя ставится следующее уравнение: ^EP = k (0) (Ex(0) - 2 • E )• (7) где E – амплитуда падающей волны. Вычис- ления показывают, что достаточная сходимость с экспериментальными данными обеспечивается при замене в (7) параметра 2 • Eo на E^ и использовании на свободном конце условия симметрии. Таким образом, авторами данной статьи предлагаются следующие граничные условия: в точке подключения генератора ^0- = k(0)(Ex(0)- Em ); (8) на свободном краю электродов dEx(Lz) = 0. (9) dz Сравним кривые распределения напряжен- ности электрического поля, полученные по формуле (4), способом [8] и путём численного решения системы (6), (8), (9). Также сопоставим результаты расчётов с экспериментальными данными, приведёнными в [11]. Здесь изучалась зависимость напряжения на электродах от расстояния до точки подключения на частотах 1,76; 5,28 и 13,56 МГц при длине конденсатора 8 м. В эксперименте конденсатор был заполнен сосновым пиломатериалом («сухая» плотность 400 кг/м3) в комнатно-сухом состоянии (влажность 8–12 %). С учётом зависимости [12] диэлектрических свойств от плотности древесины и частоты поля, а также с учётом поправки плотности на влажность [13] принимаем их равными: z = 2,2, tg^ = 0,25. Теоретические и практические кривые имеют разные размерности. Однако напряжение на электродах в конкретной точке пропорционально напряженности E в материале в этой же точке, поэтому для удобства анализа представим результаты в безразмерной форме. Для этого разделим соответствующую функцию распределения на её максимальное значение E •( z»= ' U '* z) = ■ max (|EX (z )|) max (U (z)) В этом случае величину E можно задать произвольно. Результаты показаны на рисунке 2. На частоте 1,76 МГц (рис. 2, а) отношение длин конденсатора и волны составляет 0,07. Формула (4) и система (6), (8), (9) достаточно точно предсказывают распределение напряженности электрического поля. Кривая E2, полученная способом [8], демонстрирует максимальную напряженность в точке подключения генератора, чего не наблюдается на практике. Тем не менее данный способ может быть использован при зеркальном отображении результатов расчёта (кривая E2`). Аналогичные выводы можно сделать и для частоты 5,28 МГц (L/λ = 0,2), причем наиболее точно повторяет эксперимент кривая E3 (рис. 2, б). При частоте генератора 13,56 МГц длина волны больше конденсатора всего в 2 раза. Здесь начинает проявляться затухание электромагнитных колебаний. На рисунке 2, в видно, что уровни напряженности в точке подключения и на противоположном краю одинаковы, если в расчёте пренебречь коэффициентом α (кривая E1). В то же время практика показывает снижение напряженности на противоположном краю конденсатора почти на 25 % (кривая U). На данной частоте результаты решения системы (6), (8), (9) (кривая E3) также максимально приближены к экспериментальным. Вычисления способом [8] неудовлетворительны вне зависимости от направления отображения кривой E2, поэтому он может быть использован только при малых соотношениях L/λ. в Рис. 2. Кривые распределения напряженности электрического поля и напряжения на электродах: а - результат расчёта по формуле (4); б - результат расчёта способом [8]; в - зеркально отображенная кривая б; г - результат решения системы (6), (8), (9); д - экспериментальная кривая по данным [10] Выводы. Предложен способ описания волнового распределения напряженности электрического поля на основе дифференциального уравнения Гельмгольца, дополненного авторскими граничными условиями. Полученный способ рекомендуется использовать для моделирования высокочастотного нагрева длинномерных материалов с однородными и неоднородными переменными свойствами. Полученный способ достаточно адекватно описывает распределение электромагнитного поля даже при больших величинах отношения длины конденсатора к длине волны.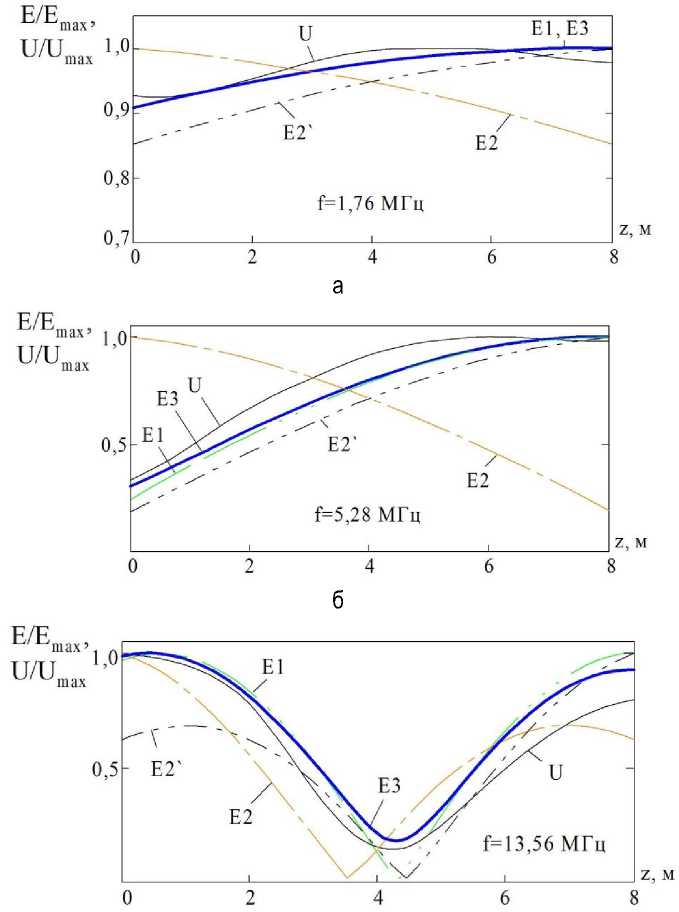
Список литературы Описание электромагнитного поля в плоском конденсаторе при высокочастотном нагреве длинномерных диэлектриков
- Марков А.В. Математическая модель СВЧ-термообработки влажных материалов//Прикладная физика. -2005. -№ 3. -С. 92-95.
- Petrescu С., Ferariu L. Modeling of dielectric heating in radio-frequency applicator optimized for uniform temperature by means of genetic algorithms//International journal of computer, electrical, automation, control and information engineering. -2008. -Vol. 2. -№ 11. -P. 3668-3673.
- Palade P.А., Vicaş S.M., Vuşcan F.B. Aspects regarding the wood processing in high fre-quency electromagnetic fields//Analele Uni-versitătii din Oradea Fascicula: Ecotoxicologie, zootehnie şi tehnologii de industrie alimentară. -2010. -P. 1207-1214.
- Hossan M.R., Dutta P. Effects of temperature dependent properties in electromagnetic heat-ing//International Journal of Heat and Mass Transfer. -2012. -Vol. 55. -P. 3412-3422.
- Качанов А.Н., Чукумов М.Н. Повышение качества сушки на ПМО “Арай”//Проблемы комплексного развития регионов Казахста-на: мат-лы Междунар. науч.-практ. конф. Ч. 1. -Алматы: Изд-во КазгосИНТИ, 1996. -С. 131-134.
- Качанов А.Н., Коренков Д.А. Повышение энергоэффективности камер для вакуумно-диэлектрической сушки//Актуальные про-блемы энергосбережения и энергоэффек-тивности в технических системах: лекции 2-й Междунар. конф. с элементами научной школы. -Тамбов: Изд-во Першина Р.В., 2015. -С. 84-92.
- Княжевская Г.С., Фирсова М.Г., Килькеев Р.Ш. Высокочастотный нагрев диэлектри-ческих материалов/под ред. А.Н. Шамова. -2-е изд., перераб. и доп. -Л.: Машино-строение, 1989. -64 с.
- Alpert Y., Jerby E. Coupled thermal-electromagnetic model for microwave heating of temperature-dependent dielectric media//IEEE Transactions on plasma science. -1999. -Vol. 27. -№ 2. -P. 555-562.
- Коренков Д.А. Распределение внутренних источников теплоты в процессе сушки дре-весины вакуумно-диэлектрическим спосо-бом//Энерго-и ресурсосбережение -XXI век: сб. науч. тр. XIII Междунар. науч.-практ. интернет-конф. -Орел, 2015. -С. 89-94.
- Jolly P., Turner I. Non linear field solution of one dimensional microwave heating//Journal of microwave power and electromagnetic en-ergy. -1990. -Vol. 25. -№ 1. -P. 3-15.
- Дьяконов К.Ф., Горяев А.А. Сушка древеси-ны токами высокой частоты. -М.: Лесн. пром-сть, 1981. -168 с.
- Torgovnikov G.I. Dielectric properties of wood and wood based materials. -Berlin: Springer Verlag, 1993. -194 p.
- Справочник по сушке древесины/Е.С. Богданов, В.А. Козлов, В.Б. Кунтыш . -4-е изд., перераб. и доп. -М.: Лесн. пром-сть,1990. -304 с.


