Определение, классификация и матричное описание преобразований петрографических структур

Одной из самых интригующих проблем современной петрографии является неопределенность ее основного предмета – кристаллической горной породы. Иначе говоря, петрограф знает много горных пород, поименованных в петрографических словарях по признакам менее или более устойчивых химического и минерального состава, структуры и текстуры. Но горная порода не определена в петрографии с той математической строгостью, с какой определен, например, кристалл в геометрической кристаллографии ( Белоусов , 1987). Напомним бытующие определения.

Горные породы – минеральные агрегаты, обладающие более или менее постоянным составом и структурой… Структура горной породы – строение, совокупность ее признаков, определяемых морфологическими особенностями отдельных составных частей и их пространственными взаимоотношениями… Текстура – особенности расположения и соотношения отдельных участков, слагающих горную породу и характеризующих степень однородности ее сложения… Морфологической единицей текстуры является минеральный агрегат, а структуры – минеральное зерно ( Левинсон-Лессинг, Струве , 1963; Петрографический словарь , 1981).

В этой связи представляется перспективным развитие представления о горной породе как пространстве ( Вернадский , 1987; 1988) – не только физическом, но и математическом, с определенными элементами и связующими отношениями. На этом фундаменте автором определена категория петрографической структуры, из чего автоматически следуют классификация и описание преобразований средствами матричной алгебры.

2.    Горная порода как пространство

Примем в качестве исходного, эмпирически обоснованного посыла, что любая горная порода как целое состоит из элементов – минеральных зерен, образующих различные сочетания (связные агрегаты и несвязные ассоциаты), на множестве которых определены фундаментальные отношения: фактической (не) тождественности, видовой (не) тождественности и пространственного (не) контактирования. Этого достаточно, чтобы различными способами определить горную породу как пространство.

Вестник МГТУ, том 17, № 2, 2 014 г. стр.266-2 70

Определение 1. Множество 91 элементов любой природы называется топологическим пространством, если оно может быть представлено как объединение некоторого семейства 3 своих подмножеств, замкнутого относительно объединения любого числа и пересечения любых двух из них. 3 называется топологией 91. Если в 91 можно выбрать семейство К подмножеств так, что каждое множество из 3 есть объединение некоторых множеств из К, то К называется базой 91 ( Вулих , 1965).

Горная порода - топологическое пространство с целым спектром топологий от тривиальной до дискретной. По-видимому, поиски фундаментального представления о принципах устройства горной породы означают не что иное, как поиски промежуточной - между указанными крайностями -топологии.

Определение 2. Отношение * называется рефлексивным, если V x : х * x ; симметричным, если V x , y: x * y =^> y * x ; транзитивным, если V x , y , z : x * y , y * z =^> x * z . Эквивалентность = рефлексивность + + симметричность + транзитивность, толерантность = рефлексивность + симметричность, строгий порядок = антирефлексивность + транзитивность, нестрогий порядок = рефлексивность + транзитивность + + антисимметричность, квазипорядок = рефлексивность + транзитивность ( Вулих , 1965).

Горная порода - пространство толерантности с определяющим (рефлексивным, симметричным, нетранзитивным) отношением неконтактирования минеральных зерен или непустого перекрытия их агрегатов. Как интерпретировать этот результат? Если изучение природы состоит в поиске структур, подразумевающих один из названных выше порядков, то пространство толерантности - не структура. Этому препятствуют наличие симметричности и отсутствие транзитивности у порождающих отношений. Но именно благодаря отказу от транзитивности толерантность есть логическое расширение эквивалентности, а пространства толерантности суть обобщения классификаций, лежащих в основаниях всех естественных наук как первый шаг, требующий шага второго. Если классификации разбивают целое на части, то пространства толерантности возвращают им целостность. Поэтому их иногда нестрого называют классификациями с размытыми границами. Концепция толерантности нетривиальным образом выражает идею целостности пространства горной породы.

Определение 3. Мерой в множестве 91 называется вещественная, неотрицательная, монотонная, аддитивная и ограниченная функция, заданная в некоторой алгебре подмножеств множества 91 ( Вулих , 1965).

Горная порода - измеримое пространство с целым спектром мер, требующих лишь ее составленности из минеральных зерен (различных видов). Для горной породы мерами будут число минеральных зерен данного вида в данном объеме пространства; их объемы; площади их сечений, измеряемые под микроскопом, и др. Меры можно использовать для определения метрик.

Определение 4. Множество 91 элементов любой природы называется метрическим пространством, если V i , j определено как вещественное число h ( i , j ), называемое метрикой (расстоянием): (1) h ( i , j ) > 0, h ( i , j ) = 0 о i = j , (2) h ( i , j ) = h(j' , i ), (3) V i , j , k =^> h (i , j ) + h (j' , k ) > h ( i , k ) ( Вулих , 1965).

Горная порода - метрическое пространство с целым спектром метрик, заданных через различные отношения минеральных зерен и агрегатов, а также их меры. Примеры метрик: h ( a , b ) = min [dist( a , b )], где dist( a , b ) - число бинарных границ на непрерывном пути из а в b в пространстве горной породы. Метрика Хаусдорфа о( A , В ) = max {{^( а , В ) | а e A }, {^( b , A ) | b в В }}, где £( а , B ) = max { h ( а , b ) | b в В }, bA A) = = max { h (b , а ) | а в A }. Метрика ^( A , В ) = р( A и В ) - ц ( A п В ). Метрика р( A , В ) = 1 - р( A п В ) / ц( A и В ), где и - мера. Корректное определение метрики позволяет создать более высокий этаж теории -о пространственной коррелируемости минеральных зерен и агрегатов различных видов.

Определение 5. Ковариационная функция c ij ( h ) = E [( x - Ex ) ( y - Ey )], где Е - математическое ожидание случайной величины ( Rivoirard, 1994).

Горная порода - частично упорядоченное пространство, в котором положение минеральных зерен и их агрегатов коррелировано: c ij ( h ) ^ 0. Заметим, что случаю пространственной некоррелируемости (т.н. случайная мозаика) соответствует c ij ( h ) = 0.

Горная порода - пространственно распределенная случайная функция, значение которой в каждой точке (т.е. минеральный вид каждого зерна) вычисляемо по его окружению ( Rivoirard , 1994; Voytekhovsky, Fishman , 2003). По-видимому, это представление о горной породе фундаментально. Оно охватывает все ее реализации и не нуждается - в отличие от кристаллографии - в противопоставлении идеального и реального.

3.    Определение и классификация петрографических структур

Из системного анализа заимствуем представления об организации и структуре. Организация -совокупность всех отношений между частями целого. Структура - совокупность принципиально важных отношений, определяющих целое, без которых оно не существует. Организацию горной породы мы фиксируем распределением вероятностей межзерновых контактов:

т\ mi тп

Ри P12 - Pm

У  п ™         [              1 Р21   Pl2 - Pin

L Pijmjmj = [да; mi - т„1

_Рп\  Р п2  "'   Рпп

По сути, из приведенной формулы следует, что горная порода представляет собой многомногозначное отображение определенного набора минералов на себя, управляемое оператором P ij вероятностей межзерновых контактов:

и

Z Ри mi mj = i,j=A

Vm^" ---^-> Vm^" .

Он представляет собой симметрическую матрицу коэффициентов квадратичной формы от n переменных, где n - число минералов в горной породе. Соответствующую квадратичную поверхность в n -мерном пространстве назовем структурной индикатрисой. Отсюда следует несколько идей. Во-первых, структуру горной породы удобно фиксировать (геометрически) индикатрисой и (алгебраически) диагональной формой матрицы вероятностей P ij .

Определение 6. Петрографическая структура - инвариант горной породы, фиксируемый (геометрически) индикатрисой и (алгебраически) диагональной формой матрицы вероятностей P ij межзерновых контактов.

Классификация петрографических структур сведена к таковой для квадратичных форм (поверхностей). "Сущность проблемы (описания геологических объектов. - Ю.В .), по-видимому, состоит в том, чтобы обнаружить такие математические структуры и алгебры, которые были бы изоморфны геологическим системам, то есть позволяли бы их описывать на математическом языке" ( Косыгин, Соловьев , 1969). Нетрудно доказать, что в принятых определениях для n -минеральных горных пород существует ровно n структур. Для би- и триминеральных горных пород все возможные структуры найдены в норитах и габброноритах Федорово-Панского массива на Кольском п-ове.

На рисунке показан условный переход от состояния 1 (эллиптический тип) к состоянию 5 (гиперболический тип). Границей является условие p и p ₂₂ = p ₁₂ ² в точке 3 (пара параллельных прямых). В геометрических образах переход состоит в непрерывном повороте и удлинении эллипса, его разрыве в бесконечно удаленных точках, изгибании пары параллельных прямых в гиперболу и ее непрерывной деформации. Соответствующие изменения в вероятностях межзерновых контактов при наблюдении петрографических шлифов неуловимы, что и сформировало устоявшееся мнение: "Петрология до сих пор не выработала никакой философской классификации горных пород… Не может быть создана никакая классификация, которая обладала бы определенностью и точностью, найденными в некоторых других областях науки… Горные породы различных типов часто связаны непрерывными переходами, так что никакая искусственная классификация с резкими разделительными границами не может истинно представлять факты природы" ( Harker , 1908).

Предложенный подход решает проблему. Всякая петрографическая структура устойчива относительно некоторых непрерывных вариаций вероятностей p ij межзерновых контактов. Но это не противоречит скачкообразному изменению типа структуры на резких (других не бывает) границах классификации. Они определяются соотношениями Харди-Вайнберга, известными в биологии как условия равновесия конкурирующих аллелей.

4.    Матричное описание преобразований

В предложенной классификации петрографических структур возможны преобразования двух типов - в пределах класса и между ними. Первые логично назвать количественными, поскольку они изменяют организацию, но сохраняют структуру, вторые - качественными, так как они меняют структуру. Преобразования первого типа - подобия - хорошо известны в алгебре и легко интерпретируемы геометрически: петрографические структуры одного типа подобны в том же смысле, что эллипсы, гиперболы, эллипсоиды, гиперболоиды, … (в пределах своего класса). Для любых двух состояний [ P ij ] и [* P ij ] горной породы с одной структурой найдется связывающее их невырожденное преобразование подобия [ Q ]:

[* P j ] = [ Q ]^т [ P ij ] [ Q ].

Вестник МГТУ, том 17, № 2, 2014 г.    стр.266-270

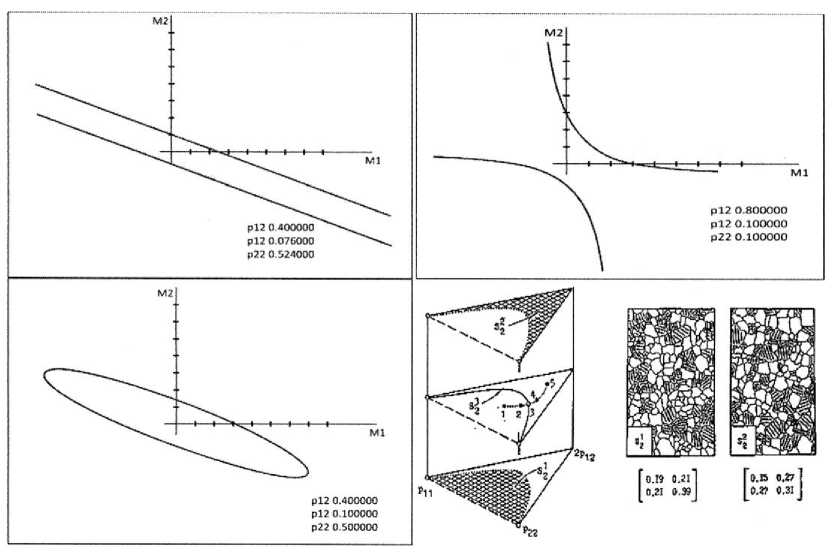
Рис. Соотношение биминеральных петрографических структур на примере норитов Федорово-Панских тундр, Кольский п-ов

Все преобразования подобия образуют мультипликативную группу ( Гантмахер , 1988).

Описание качественных преобразований представляет не столь тривиальную задачу, легко понятную геометрически. Например, как преобразовать эллипс в гиперболу, эллипсоид в одно- или двуполостный гиперболоид? Наша идея состоит в том, чтобы сначала описать переходы между специальными представителями классов, характеризуемыми каноническими формами матриц [ P ij ] с ± 1 на диагоналях. Для этого использованы те же диагональные матрицы, образующие мультипликативную группу. Переход от канонической матрицы к любому представителю того же класса выполняется как преобразование подобия, описанное выше.

5.    Заключение

Историкам и философам естественных наук еще предстоит понять, почему до сих пор не была создана теория строения кристаллической горной породы из видимых элементов – минеральных зерен, хотя теория организации кристалла из невидимых атомов известна уже 100 лет. Мы не знаем, какую математическую идею заложила природа в кристаллические горные породы, в том смысле, что в кристаллы она заложила идею 230 пространственных групп Федорова-Шенфлиса. Автором разработано связное представление о горной породе как топологическом, толерантном, измеримом, метрическом и коррелированном пространстве, не претендующее на полноту. Для одной горной породы могут быть определены различные топологии, меры и метрики. Тем самым одно пространство получает взаимно дополняющие представления. Такая относительность не противоречит тому, что одно из них может оказаться фундаментальным, характеризующим пространство горной породы наиболее рационально. Так, кристаллическое пространство "строится" на волновых и корпускулярных представлениях. Но лишь во втором случае выводимы федоровские группы, признанные его фундаментальным представлением. Подчеркнем, что в предложенных подходах ключевую роль играет категория пространства, систематически введенная в естественные науки В.И. Вернадским.