Определение количества альтернативных маршрутов для выполнения с заданной вероятностью задачи сетевого обмена

Выполнение задач сетевого обмена в информационно-вычислительных сетях (далее – ИВС) предполагает построение нескольких альтернативных (проходящих через различные транзитные узлы сети) маршрутов для обеспечения с заданным уровнем надежности обмена данными между конечными узлами – узлом-источником и узлом-приемником.

Формирование требуемых маршрутов (подбор допустимых промежуточных узлов) возможен в рамках маршрутизации от источника.

Однако при использовании общедоступных (публичных) сетей даже с использованием технологии VPN-каналов для каждого маршрута возможна компрометация (случайная или намеренная) активного маршрута и, как следствие, признание его отказавшим с переключением на другой альтернативный маршрут. Отказавший маршрут не восстанавливается и исключается из альтернативных.

Определение количества альтернативных маршрутов для выполнения с заданной вероятностью ...

Баглюк Сергей Иванович кандидат технических наук, доцент, преподаватель кафедры информационно-вычислительных систем и сетей, Военно-космическая академия имени А.Ф. Можайского, Санкт-Петербург. Сфера научных интересов: информационно-вычислительные системы и сети. Автор более 30 опубликованных научных статей.

Под компрометацией маршрута будем понимать его физическое разрушение, критическое снижение пропускной способности, перехват, перенаправление или подмену трафика.

Ранжирование последовательности активации маршрутов (назначение альтернативным основному и резервным, маршрутам метрик) [1] будем полагать эквивалентным определению для каждого из них вероятности безотказного функционирования [2]. Детальное рассмотрение технологии сбора статистических данных об отказах маршрутов и формирования на их основе законов распределения вероятностей безотказного функционирования (вероятностей отказов) маршрутов выходит за рамки данной работы. Отметим лишь, что эта рутинная задача может быть решена сетевыми администраторами с использованием штатных средств анализа сетей, например, встроенными в сетевое программное обеспечение программами (утилитами) pathping (ping , tracert) в среде Windows или mtr (ping , traceroute) в среде Linux и математическим аппаратом обработки статистических данных для построения законов распределения вероятности отказа каждого из маршрутов.

Постановка задачи

Рассмотрим подход к определению минимально необходимого количества альтернативных сетевых маршрутов для гарантированного выполнения задачи сетевого обмена в ИВС.

Полагаем, что закон распределения вероятности отказа каждого из маршрутов известен и в процессе их эксплуатации корректируется, результат корректировки учитывается оперативно.

Тогда задача определения требуемого (в смысле надежности) количества резервных маршрутов сводится к задаче отыскания необходимого количества резервных элементов резервированной системы с ненагруженным резервом без восстановления, описываемой интегральным уравнением Вольтерры второго рода [3]. Общий вид такого уравнения

T

Р_дир(Т) = P_OM(T) + \ a _B . ( т ) P _pe3 ( ^T -т ) d T ,                      (1)

где                                                 0

Pдир(T) – директивно заданная вероятность безотказного функционирования ИВС в течение времени T;

Pом(T) – вероятность безотказного функционирования основного маршрута сети в течение времени T;

а _ом ( т ) — плотность распределения вероятности отказа основного маршрута сети в случайный момент времени т , 0 <  т <  T ;

P _pe3 ( T -т ) - вероятность безотказного функционирования последовательно подключаемых (вместо отказавшего основного) резервных (альтернативных) маршрутов на интервале ( т , T ).

Решение задачи

Рассмотрим задачу при произвольном законе распределения вероятности отказа каждого из маршрутов. Сомножитель второго слагаемого уравнения (1), отображающий интегральную вероятность безотказного функционирования последовательно подключаемых (взамен отказавших) альтернативных маршрутов, разворачивается (пример одного основного и четырех резервных альтернативных маршрутов) в следующее выражение:

T

^P c (T) = ^P _OM (T + j a oM ( т ) P _pe3 ( ^T -т ) ^d т = P _OM (T) +

TT

1 ^а ом ^{(т ) {} P 1 ^{( T -т ) +} a ^{( т} 1 ^{) [} P 2 ^{( T -т - т} 1 ^{) +}

0                           т

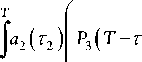
T

^-т 2 ⁾⁺ [ a 3 ( ^т 3 ) P 4 ( ^{T -т - т} 1

^-т 2 ^-т 3 ) ^{d т} 3

d т ₂ ] d т ₁ } d т

где

Pc(T) – вероятность безотказного функционирования ИВС в течение времени T, обе- спечиваемая включением основного и четырех резервных альтернативных маршрутов;

т1, т2 , т3 - случайные интервалы времени (т,т1), (т1,т2 ), (т2,т3 ) работы между отказами последовательно подключаемых (взамен отказавших) первого, второго и третьего резервных маршрутов соответственно; время на переключение маршрутов из рассмотрения исключаем;

а 1 ( т 1 ) , а 2 ( т 2 ) , а 3 ( т 3 ) - плотности распределения вероятности отказа альтернативных первого, второго и третьего альтернативных маршрутов соответственно,

P 1 ( t -т ) , P 2 ( t -т-т 1 ) , P ₃ ( t -т-т 1 -т 2 ) , P ₄ ( t -т-т 1 -т 2 -т 3 ) - вероятности безотказного функционирования первого, второго, третьего и четвертого из резервных альтернативных маршрутов сети в течение временных интервалов ( T -т ) , ( T -т-т 1 ) , ( T -т -т 1 -т 2 ) и ( T -т -т 1 -т 2 -т 3 ) соответственно.

Последовательность случайных интервалов времен работы до отказа маршрутов иллюстрирует Рисунок.

Определение количества альтернативных маршрутов для выполнения с заданной вероятностью ...

Рисунок. Последовательность случайных интервалов времен работы до отказа основного и резервных маршрутов

Источник: рисунок выполнен авторами.

Сравнивая далее директивно заданную вероятность безотказного функционирования ИВС на интервале (0,T) Pдир(T) с числовым значением, получаемым в результате подстановки в правую часть уравнения (2), рассчитанных на основе статистических данных об отказах числовых значений показателей надежности основного и альтернативных маршрутов, добиваемся того, чтобы уравнение (1) превратилось в нестрогое неравенство: левая часть уравнения оказалась меньше либо равна правой его части: Pдир(T) ≤ Pc(T).

Тогда при соблюдении условия полученного неравенства количество альтернативных маршрутов будет равно количеству сомножителей в правой части неравенства.

В качестве упрощенного примера рассмотрим сеть, включающую основной и один резервный маршрут; распределения вероятностей отказов основного и резервного маршрутов подчиняются экспоненциальным распределениям с различными интенсивностями отказов. Интервал Т = 1000 ч. Директивно заданная вероятность безотказного функционирования ИВС на интервале (0,T) Pдир(T) = 0,99.

Положим, что надежностные характеристики маршрутов имеют следующие числовые значения:

POM(T) = 0,85; \М = 0,000163[1/ч];

P“(T) = 0,75 £“ = 0,000288 [1/ч];                         (3)

Тогда выражение (2) принимает следующий вид:

T p.m = p.M (T) + \a0. (t ) p,, ( T-T ) dT

T

= P (T) + t = P (T) + A_nM e - *1"' f e^(Л 1 ^{p 7 T} T = 0,977 (4)

OM             OM         ^OM

Таким образом, сеть, включающая основной и один резервный маршруты с характеристиками, указанными в (3), не позволяет (4) выполнить условие Pдир(T) ≤ Pc(T), что требует включения в рассматриваемую схему еще одного резервного маршрута. Выражение (2) в этом случае трансформируется:

T

T

^P c ^(T) = ^P OM ^{(T) +} \ a o« ( ^T ) { ^P 1 ( ^T — ^T ) + a ( ^T 1 ) ^{[ P} 2 ( ^T — ^{T - T} 1 ) ^] d ^T 1 ^{} d T} .

0 ^t

Далее следует подстановка в (5) числовых значений характеристик второго резервного маршрута и проверка выполнения условия Pдир(T) ≤ Pc(T). Итерации следуют до выполнения указанного условия.

Заключение

Рассмотрен подход к определению необходимого количества резервных сетевых маршрутов для выполнения с директивно заданной вероятностью задачи сетевого обмена в информационно-вычислительных сетях при следующем ограничении: отказавший маршрут не восстанавливается и для дальнейшей эксплуатации не рассматривается. Подход опирается на построение сетевых маршрутов в общедоступных (публичных) сетях с использованием маршрутизации от источника.

Решение сформулированной задачи базируется на представлении совокупности альтернативных маршрутов в виде резервированной системы с ненагруженным резервом без восстановления, анализе выявленных законов распределения времени наработки на отказ для каждого из маршрутов и формулировании вывода о необходимом их количестве.