Определение области осаждения аэрозоля с помощью фракционной модели

Проблема определения зоны выпадения токсичных осадков вокруг промышленных зон в настоящее время весьма актуальна. Многие токсичные вещества выбрасываются в атмосферу промышленными объектами в дисперсном или в газообразном состоянии, после чего они могут взаимодействовать с каплями туманов и облаков, образуя токсичный аэрозоль, который переносится воздушными массами и может выпадать в виде осадков.

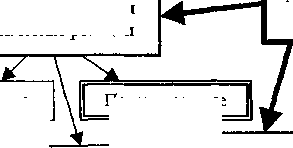
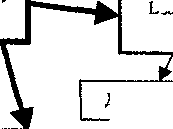
Накопление примеси в каплях аэрозоля, перенос капель в атмосфере и их выпадение сопровождаются различными процессами, которые можно условно разделить на четыре основные группы (рис. 1). Однако, если ограничиться невысокими скоростями ветра, положительной температурой воздуха, а также отсутствием химических реакций в каплях, то количество процессов, рассмотрение которых необходимо для моделирования образования и выпадения токсичных осадков, можно существенно уменьшить.

Объемные

Фазовые переходы и химические реакции

Поверхностные

Нуклеация

Взаимодействие с потоком

Аэрозольные процессы

Дробление__|

Воздействие внешних сил

Взаимодействие частиц

Коагуляция

__^ Электромагнитное воздействие

Аэродинамические деформация и дробление

Перенос и диффузия

Срыв частиц с поверхности

Гравитационная седиментация

Рис. 1. Процессы происходящие с атмосферным аэрозолем

В настоящее время исследованию процесса накопления и переноса примеси атмосферным аэрозолем уделяется много внимания. Однако известные в настоящее время работы, посвященные данному вопросу, концентрируются на моделировании одного или нескольких процессов и поэтому не обладают необходимой полнотой. Так, в [1] наряду с учетом поверхностных фазовых переходов игнорируется процесс коагуляции, являющийся, по существу, определяющим фактором роста капель. В работах [2, 3, 4], напротив, рассматривается только процесс коагуляции. Исследование [5] наиболее полно охватывает процессы массообмена, однако, как и во всех упомянутых ранее источниках, исследуются только моменты распределения капель по массе составляющих их веществ, чем достигается высокая эффективность методов, при этом теряются детали распределения, которые важны при исследовании выпадения токсичных осадков. Кроме того, во всех указанных работах рассматривается пространственно однородный случай. В [6] исследуются перенос и диффузия токсичного аэрозоля с учетом коагуляции, однако не учитывается наличие в атмосфере чистого водного аэрозоля, не рассматривается также и массообмен на поверхности аэрозольных частиц.

Таким образом, существует необходимость построения модели, описывающей образование, перенос, диффузию и выпадение токсичных осадков с учетом коагуляции, нуклеации, поверхностных фазовых переходов и гравитационной седиментации.

Постановка задачи

Для простоты рассматриваются однородные по объему капли, которые находятся в газовой смеси, состоящей из воздуха, паров воды (с концентрацией с^) и 5 загрязняющих веществ (с концентрацией £^,7 = 1,5). Вводится функция распределения капель /(/,х.//⁰⁾,...,//^) по массе содержащихся в них воды ц^-1' и загрязняющих веществ//', 7 = 1,5 в каждый момент времени / в произвольной точке рассматриваемой области х Кинетическое уравнение баланса в фазовом пространстве записывается в виде

^ + V.l)/ + £--+                         (1.1)

.=o        '

Здесь второе слагаемое в левой части описывает перенос капель со скоростью U^x,^^,...,^1*^; третье слагаемое описывает увеличение или уменьшение размера капель за счет фазовых переходов на поверхности капель и сорбции или десорбции Ж. т (о)     (s) (о) (sh примеси жидкостью, при этом 1 \t,x,l,c ,...,с ^/л ,...,ц    — скорость измене ния массы /-го вещества в капле; первое слагаемое в правой части описывает диффузию капель как пассивной примеси, D^t, х, Т, т) — коэффициент диффузии; второе слагае-/        (о)      (s) (о)      (s)\ мое описывает гомогенную конденсацию, J /,х,Т,с ,...,с ,ц           —скорость нуклеации капель; функционал ok^,xj Ж\---^^ описывает взаимодействие капель — исчезновение мелких капель и увеличение количества крупных капель при коагуляции, функция G(/,x,m) описывает гравитационную седиментацию.

Решение уравнения (1.1) совместно с уравнениями движения, а также переноса водяного пара и газообразных примесей, позволит описать образование, перенос и выпадение токсичных осадков.

Фракционная модель

Далее, во избежание громоздких формул, рассматривается случай одной примеси (5 = 1), рассуждения для произвольного количества примесей 5 в пространственно од- нородном случае без учета седиментации приведены в [7]. Следуя этой работе, функция / аппроксимируется кусочно-постоянной функцией по аргументам //" следую щим образом:

где ^^ = 0 (//^— масса вещества в критическом зародыше), h() — ступенчатая функция Хевисайда. Будем считать, что капли, удовлетворяющие неравенствам (0) / (0)      (0)        (1) . (1)      (1)                                      „ , р < р <ри р. < р < р, принадлежат к одной фракции, при этом все капли,

„ ,                                                                 (0) (О принадлежащие к одной фракции, имеют одинаковую массу т^- р + р. .

Используя гипотезу о взаимопроникающих континуумах и рассматривая каждую фракцию как «газ» одинаковых частиц, можно ввести распределенную плотность фракции, которая определяется соотношением

(о) ^(1)

f , , (0) , М               Л (0)А (1)                         „ _ где Др = р +[ - р , и?( ^ ^ = (m^.^^+ m J/2 . Далее для простоты принимается гипотеза об односкоростной однотемпературной среде, когда несущая газовая смесь и все «газы» частиц в каждой точке имеют равную скорость и температуру.

Умножая обе части уравнения (1.1) на массу капли т и шгтегрируя по массе в пределах одной фракции, используя аппроксимацию (2.1), можно получить уравнение баланса распределенной плотности для каждой фракции:

— р +V-U р = D Др + J + сг -G +--^--

Л V’ ^чИи^РИ^г (0) (0) 1|АЛ^о) W 0) tW WA ^лр-^^тИИ

‘ V’ H\jH)^PHV_ (1) /о 1А/0      (0) (О (0) (О     (о) А

> ——m~----- ²А ч ,+- 47, _|V .р, ,.+/, .р + Z, „ .и

=-i zxp т, _v , l                      ⁴

j*4 Hki+q+i)

Функция Z(x,y) = (-l)xh(l-2xsgn(y))sgn(y) определяет направление процессов массо-обмена. Эта функция, в зависимости от аргументов, принимает значения

у < 0 у - 0 у > 0 х = -1 1       0      0 х = 0 -1      0      1 Х = 1 0     0    -1, что позволяет ей «включать» и «выключать» щие обмен массой с другими фракциями.

соответствующие слагаемые, описываю-

Выражение в правой части (2.3) описывает увеличение числа капель в рассматриваемой фракции, в первой и второй сумме соответственно, за счет конденсации водяно- го пара и поглощения примеси каплями меньшего размера (q = -1); испарение жидкости и выделение примеси каплями большего размера (с/ -1), при q = 0 обе суммы описывают уменьшение количества капель за счет перехода в другие фракции.

Как и в [7], коагуляция описывается с помощью модели Смолуховского. Для капель, состоящих из двух веществ, можно записать:

X <^{0)              (0)}  0) ~(°) ~O)V/~(o) ~(1)V~(O)  0)

сгМ,Ц ,Д I =                                   A -А «А +

(°) ~(°) и -(ОЪГ-П ~(ГА / (о) ДО) (1)

К ц ,р ,р -р ,р -р Дд ,р /д -р ,р где К — ядро коагуляции, которое определяется величиной вероятности столкновения капель различных размеров с последующим слипанием. Для простоты предположим, что для любых двух фракций ядро коагуляции остается постоянным в пределах каждой из фракций. Тогда для случая одной примеси [7]

j р+1 5+1 р+1 5+1

( (о) (1)     (0) (1)

> р К \ш ф + ф ы rpkl цНк ik ^Т jl ^ik ^Y jl

РЧ                                ,

2 z—¹"                                , (о) (1) (оТ" (ГУ¹

^ /=о j=ok=Q z=o т, _]V ап, _|V .Дп Дд Дд Дд У+гЛт+г) (^"ЧЛ' + г) i ] к I

(2.4)

где

Y ^   (?)Y (?)2   Y)2 Д ( ’л)   YY I?)2

— p + p д -p , - \p + p д 2 <  '+1    ⁴⁺¹А  ⁴^     ³P’k)  у '        •=■ )\_ ip*

k)2 - д pik

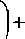
. ( . (?) . (?)Y (?)² + min Дд ,Дд p

JX^ipik

- p

“2 pik

_ (?)3

З^Х pik ^2pik

№ (D ) , + p

3 pik   ~4 pik J

(9)    (  (?)

ф . = i p ^Y pik    \ i-v\

(?)Y (?)    (?) ( (?) W X (?)

+ p p - д - д + p д - p

“ку\Д'4рк 3pik ) у i ' к 9/ 2pik 'ipik

+ minlA/z. ,Ap_fc |;Д_3м1

(?) A Y (9)2    (?)2

- и — p - p

(?)2      («/z \

A + Ц

"Зргк "^pik j

tp . Г / (0 (,) on 0) p = min max p _p + p, , p ^lljk        l Щ1 ’              У ^л /+1

(-) f (-) • ( 0)      0) 0)Y

=max ,min \p + p ,u i, ^4ljk                     I '+1 ^!:+1’П+1 I ’

M . (    ( (-) . ( G) 0) 0)     0)Y (Y)

p = min max д , min \p +p +p        i

2Й-                       4 ^{2+1 k} Ы

(-)     . f Г G) ( G) 0) G^ GW on p =min max zz ,max\ и +p ,p + p \Vp к ЗЦк I V * V 7+1                    j            J

Громоздкий вид второй суммы в правой части (2.4) обусловлен произвольностью выбора ар , однако поскольку р. не зависят от времени, выражение в скобках явля ется постоянным множителем. Кроме того, большинство слагаемых во второй сумме остается нулевым на протяжении всего процесса.

Как указывалось выше, полученную систему дифференциальных уравнений необходимо дополнить уравнениями диффузии пара и примеси, которые с учетом высказанных предположений об односкоростной многоконтинуальной среде могут быть за писаны в виде

——hv Uc -N D vc +Б -JjA dp dp , ^ot                                          0 0

где с - концентрация i-го вещества, В - источники и стоки i-ro вещества

Используя аппроксимацию (2.1) для случая одной примеси и считая коэффициент диффузии постоянным по пространству, можно получить

ОС

---+ V • Uc dt

N М i

,=1 >0

Теперь, задаваясь конкретными зависимостями для скоростей массообмена, седиментации и нуклеации, а также граничными и начальными условиями, можно, пользуясь построенной фракционной моделью, получить решение рассматриваемой задачи.

Простейший случай

Для примера применения фракционной модели рассматривается решение одномерной задачи распространения токсичного аэрозоля, первоначально состоящего только из загрязняющего вещества, во влажной атмосфере в постоянном поле скорости. В данном случае рассматривается плоский вертикальный слой высотой Н и длиной L, предполагается перенос и диффузия аэрозоля и пара только в горизонтальном направлении, совпадающем с направлением ветра, горизонтальные скорости аэрозольных частиц всех размеров, пара и воздуха равны U, однако вертикальная скорость оседания частиц V зависит от их массы. Концентрация пара и распределенные плотности фракций предполагаются однородными по высоте слоя. Нуклеация для простоты пренебре-гается.

Для определения скорости конденсации пара используется закон Максвелла,

Зт

■ (0) Ф)

с -с

V            4лр к °° У к х У где р — плотность жидкости капли, с\р — равновесная концентрация пара при данной температуре.

Поскольку используется односкоростное приближение, т.е. относительные горизонтальные скорости отсутствуют, можно рассматривать только гравитационную коагуляцию. В этом случае [8]

ijkl - 71

и

где г -з ч \

радиус частиц, ЕуЫ = Е^,гы) - коэффициент захвата в атмо- сфере. Скорость оседания частиц каждой фракции под действием силы тяжести определяется законом Стокса, gm

V =-- ч бтгпг

У где у - вязкость воздуха, g - ускорение свободного падения.

Скорость уменьшения распределенной плотности фракции за счет осаждения частиц, с учетом однородности по высоте слоя, определяется по формуле [9]:

Г

G ч Н ч

Поскольку при моделировании токсичных осадков наибольший интерес представляют область их выпадения и количество выпавшего вещества в различных точках подстилающей поверхности, имеет смысл ввести переменные р (х), описывающие плотность выпавшей i-той примеси на подстилающую поверхность в точке х . Соответствующее уравнение для единственной примеси в одномерном случае будет иметь вид

Построенная система уравнений дополняется начальными условиями рЛх$=РоАх\ cQ\x^=Co4x\ Р'ЧхР^ РоХА

Для определенности предполагается,что U > 0, тогда граничные условия на входной границе (х = 0 ) задаются в виде а на выходной границе (х = L)

Результаты

Для численного решения задача разбивается на две подзадачи. Первая, о переносе газов и частиц аэрозоля в пространстве, решается с помощью конечно-разностного метода с абсолютно устойчивой схемой. Вторая, о перераспределении массы между фракциями, газами и об осаждении примеси в каждой точке, решается с помощью метода Рунге-Кутта.

В качестве иллюстрации полученных результатов приводится решение задачи с / \ (0 / *> (о)

граничными условиями /уДОу^-ЛГ е , р_Х6\0,1) = М , а для остальных фракций /?„ (од)= 0. Такое задание условий соответствует кратковременному выбросу монодисперсно й аэрозольной примеси во влажную атмосферу от наземного источника (Я = 1).

На рис. 2 представлен график эволюции зависимости плотности выпавшей примеси от расстояния. Отчетливо просматривается конкуренция двух пиков, вызванная ростом частиц. Левый пик, ярко выраженный на ранних стадиях процесса, обусловлен высокой плотностью мелких примесных частиц, поступающих через входную границу. С течением времени поступление частиц снижается, однако за счет конденсации и коагуляции появляются более крупные частицы, оседание которых протекает более интенсивно, что приводит в конечном счете к росту правого пика

« 6 » г р”10”(кг/„)

Рис. 2. График плотности выпавшей примеси в различные моменты времени: а) при t = 5с ; б) при t = 10 с, в) при / — 15 с; г) при / = 20 с

На рис. 3 приведены распределенные плотности фракций в различных точках области. В начальной области (рис. 3,а) присутствуют чисто водяные капли, но уже к середине области (рис. 3,6) они исчезают образуя, смешанные капли, при этом спектр частиц остается практически неизменным до конца области (рис. 3,в).

в

Рис. 3. Фракционный состав при t = 15 с в точках, a) x = Z/4; б) х = £/2; в) x = 3Z/4

Выводы

Предложена модификация фракционной модели, которая позволяет описывать процессы осаждения токсичного аэрозоля на подстилающую поверхность. Рассмотрен достаточно простой случай распространения аэрозольной примеси в атмосфере. Несмотря на простоту задачи, решение позволило выявить влияние деформирующегося спектра частиц на вид зависимости плотности выпавшей примеси от расстояния. В начальной стадии процесса более интенсивно осаждаются мелкие частицы, фракция которых имеет большую распределенную плотность. На более поздних этапах доминирующим становится осаждение крупных смешанных частиц, появление которых обусловлено коагуляцией и конденсацией водяного пара на поверхности частиц.