Определение параметров слоя рассеивающих неоднородностей, формирующих когерентное эхо, по данным Иркутского радара НР

В работе представлена методика определения параметров слоя рассеивающих неоднородностей , формирующих когерентное эхо , по данным Иркутского радара некогерентного рассеяния . Показано , что использованная методика обладает необходимой точностью . Обработка данных экспериментов 25–26.09.1998 и 15–16.07.2000 показала хорошее соответствие получаемых результатов с данными остальных исследователей . Эксперименты с высоким временным разрешением позволили выявить временную зависимость определяемых параметров . Изменение толщины и высоты слоя от времени не противоречит данным других исследований , а временная зависимость угловой чувствительности неоднородностей от времени наблюдается впервые и требует дополнительных исследований .

This paper presents a method for determining parameters of the layer of scattering irregularities, which form coherent echo, from the Irkutsk Incoherent Scatter Radar data. This method is demonstrated to have the desired precision. The processing of experimental data for the periods of 25–26 September 1998 and 15–16 July 2000 showed a good agreement between our results and the data obtained by other researchers. The analysis of experiments with high time resolution revealed time dependence of the parameters under study. Time change of the layer thickness and height agree with data obtained by other researchers, while the time dependence of angular sensitivity of irregularities has been observed for the first time and invites further investigations.

Введение                                          Вследствие особенностей расположения и конст-

Одним из важных эффектов, оказывающих влияние на ионосферное и трансионосферное распространение радиоволн, является рассеяние на неоднородностях различных масштабов. Поэтому при изучении ионосферы значительное внимание уделяется диагностике ионосферных неоднородностей. Менее распространенными в средних широтах, но наиболее сильно влияющими на распространение сигналов являются неоднородности, ориентированные вдоль магнитного поля Земли. Рассеяние на подобных неоднородностях обладает резко выраженной ракурсной чувствительностью, приводящей к сильной зависимости амплитуды рассеянного сигнала от ориентации падающей и рассеянной волны. Один из физических механизмов формирования подобных неоднородностей в Е-слое ионосферы – развитие двухпотоковой и градиентно-дрейфовой ионосферных неустойчивостей. В качестве условий развития подобных неустойчивостей указывают сильное электрическое поле, высокую скорость движения электронов относительно ионов или наличие резких градиентов электронной концентрации [1, 2]. Такие неоднородности наблюдаются в полярных и экваториальных широтах и способны влиять на принятый сигнал в диапазоне от 8 МГц до более чем 1 ГГц [3]. Наиболее часто условия формирования этих неоднородностей на средних широтах выполняются во время больших геомагнитных возмущений, в то время как в полярных и экваториальных широтах эти условия выполняются и в менее возмущенной геомагнитной обстановке [3–5]. Радиосигналы, рассеянные на подобных неоднородностях, известны как радиоаврора, или когерентное эхо (КЭ). Сигналы КЭ наблюдаются на Иркутском радаре НР с 1998 г. За прошедшее время наблюдалось несколько крупных геомагнитных возмущений, сопровождавшихся КЭ [6].

рукции радара НР [7], рассеянный сигнал обычно имеет два четко выраженных пика в профиле средней мощности ~550 и 1100 км по дальности, на которых условие перпендикулярности луча зрения к магнитному полю в области Е-слоя выполняется наиболее хорошо. Как показал предварительный анализ, форма пиков и их положение на профиле мощности зависят от параметров рассеивающих неоднородностей. Задачей данной работы являлось определение параметров рассеивающих неоднородностей в рамках общепринятой модели. Эта задача не нова. Подобные эксперименты проводились на некоторых радарах, использующих поворотные антенны либо антенны с достаточно узкой диаграммой направленности [4, 8] или работающих в области экватора [9, 10]. Это позволяло определить расположение и форму рассеивающей области – высоту (~110 км) и толщину (~10 км) – и иногда различить несколько слоев [4, 5]. Зависимость ракурсных характеристик рассеяния от угла к магнитному полю также исследовалась, что давало средние оценки около 15 дБ/градус [8]. Проведение подобных экспериментов позволяет также осуществлять проверку моделей рассеивающих неоднородностей и косвенно проверять модели поведения нейтральной атмосферы на высотах Е-слоя [10, 11], поэтому определение и исследование параметров рассеивающих неоднородностей является важной геофизической задачей.

Задача определения высоты и толщины слоя с неоднородностями проста в случае, когда такой слой тонок и ориентирован поперек луча зрения – тогда высота слоя с неоднородностями может быть оценена как средняя задержка сигнала, а толщина слоя – как средний разброс задержек, на которых наблюдается рассеянный сигнал. Однако подобная геометрия эксперимента существует только в экваториальных об- ластях, где магнитное поле ориентировано горизонтально и луч зрения, перпендикулярный магнитному полю, вследствие ракурсных свойств рассеивателей расположен вертикально, перпендикулярно слою с неоднородностями.

На средних и высоких широтах луч зрения ориентирован под малым углом к слою с неоднородностями (практически вдоль него), что дает возможность приемлемой оценки высоты и толщины слоя только в случае достаточно острой диаграммы направленности антенны. Как будет показано далее, в случае с Иркутским радаром НР, обладающим очень широкой диаграммой направленности антенны в направлениях, с которых приходит рассеянный сигнал, подобные методики неприменимы, и поэтому определение параметров слоя с неоднородностями встречает существенные трудности.

Например, это не позволяет получить данные о параметрах слоя с неоднородностями без привлечения дополнительной информации, в частности без модели, описывающей ракурсные характеристики рассеяния. Поэтому задачей данной работы являлось получение устойчивого алгоритма определения этих характеристик слоя рассеивающих неоднородностей по форме профиля мощности с привлечением общепринятой модели, описывающей ракурсные характеристики рассеяния.

Модель рассеянного сигнала

Геометрия эксперимента приведена на рис. 1. Иркутский радар НР – однопозиционная установка; он излучает последовательность радиоимпульсов, принимая после каждого импульса рассеянный сигнал и усредняя рассеянную мощность от импульса к импульсу. Широкая диаграмма направленности позволяет анализировать рассеянный сигнал, приходящий с дальностей 200–1200 км практически одновременно с хорошим временным разрешением (несколько минут) и пространственным разрешением около 15 км, определяемым длительностью зондирующего импульса. Достаточно подробно геометрия эксперимента и параметры радара рассматривалась в [12]. Однако именно эта особенность, очень удобная для интерпретации экспериментов, не дает возможности провести оценку других важных физических параметров, в частности высоты и толщины слоя с неоднородностями, вызывающими рассеяние.

Для решения поставленной задачи проведено численное моделирование зависимости мощности сигнала, рассеянного на неоднородностях, образующихся во время сильных геомагнитных возмущений в Е-слое ионосферы и вытянутых вдоль магнитного поля Зем-

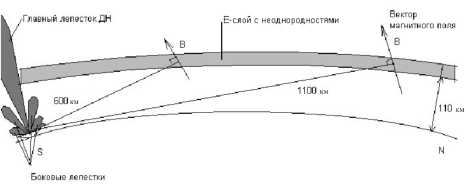
Рис . 1. Геометрия эксперимента .

ли (когерентного эха), от радиолокационной дальности и параметров слоя с рассеивающими неоднородностями. Используемая модель зависимости средней мощности рассеянного сигнала от радиолокационной дальности (профиля мощности P ( R )), учитывающая ракурсную зависимость рассеянного сигнала в экспоненциальном виде [8], с точностью до постоянных множителей имеет вид:

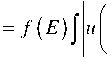
g

l ^r)

(^-А r

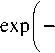
h - h₀ A h

x exp

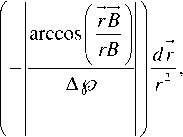
x

где f ( E ) – множитель, определяющий зависимость сечения рассеяния неоднородностей от электрического

( R - r поля; u I 2-----I - форма излучаемого сигнала;

l c )

g

(^-A r

– форма диаграммы направленности радара;

h - высота в точке рассеяния; h 0 , A h и А р - высота слоя, его толщина и угловая чувствительность соответственно; B - вектор магнитного поля; г - радиус-вектор, проведенный из точки наблюдения в точку рассеяния.

Из структуры уравнения (1) видно, что множитель

а ( R ) = f ( E ) exp| ^- h—h ⁰-1exp l A h )

arccos

-^A rB rB l )

Ap

является сечением рассеяния неоднородностей. При этом зависимость сечения рассеяния от направления определяется последним сомножителем, зависимость сечения рассеяния от высоты (оно, в свою очередь, определяется так называемым линейным решением дисперсионного уравнения для плазменных неустойчивостей [1–2] и зависит от многих параметров: высотного хода частот столкновений электронов и ионов с нейтральными частицами, гирочастот электронов и ионов, величины электрического поля, зависимости ионно-звуковой скорости от высоты) – средним сомножителем, а зависимость сечения рассеяния от остальных фоновых ионосферных параметров (не учтенных линейным решением [1, 2] – сильного электрического поля и его градиентов, фоновой электронной концентрации и ее градиентов, температур заряженного и нейтрального компонентов и других неучтенных величин) вынесена в множитель f(E). Произведение первых двух множителей определяет интенсивность рассеивающих неоднородностей, а третий множитель – их ракурсные характеристики. Следует отметить, что в настоящее время отсутствует адекватная нелинейная теория двухпотоковых и градиентно-дрейфовых неустойчивостей, позволяющая корректно ввести зависимость сечения рассеяния от фоновых ионосферных параметров (в нашем случае представлена как f(E)), поэтому используются всевозможные эмпирические модели для учета таких зависимостей, например [13]. Используемые эмпирические зависимости и методы их получения могут быть достаточно сложными [14], однако наиболее проверенной многими исследователями на этих частотах зондирования [15, 16] (на которых можно пренебречь градиентно-дрейфовым механизмом развития неустойчивостей и учитывать только двухпотоковый), с нашей точки зрения, можно считать пропорциональность логарифма рассеянной мощности электрическому полю. Таким образом, множитель f(E) определяет зависимость сечения рассеяния от фоновых ионосферных параметров, но в нашем случае предполагается зависящим только от электрического поля.

Расчеты проводились на основе международной справочной модели магнитного поля (IGRF) и используемой нами во многих задачах моделирования диаграммы направленности антенны Иркутского радара НР. В качестве модели рассеивающих неоднородностей выбирался гауссовый слой неоднородностей, характеризуемый высотой h и толщиной Δ h . Спектральная плотность неоднородностей, определяющая ракурсную зависимость мощности рассеянного сигнала от угла с магнитным полем Земли, была выбрана в виде гауссовой функции, определяющейся угловой чувствительностью Д р и углом между лучом зрения и магнитным полем Земли. Влияние внешнего электрического поля E на мощность сигнала было учтено выбором некоего масштабирующего множителя. Форма излучаемого сигнала u ( t ) также учитывалась. Начало координат соответствует положению центра антенны.

На рис. 2 приведены формы профилей мощности, полученных с помощью используемой модели при различных значениях высоты h, толщины Δh, угловой чувствительности Др. График, изображенный сплошной черной линией, соответствует профилю мощности при средних параметрах слоя с неоднородностями. Из рисунков видно, что профили при различных значени- ях параметров могут существенно меняться.

Неизвестные параметры h, Д h, Д р определялись по экспериментально измеренным профилям мощности методом поиска максимума функции корреляции на сетке заранее насчитанных модельных значений профиля (2). Индексы mod и exp у профилей мощности обозначают соответственно посчитанные по модели и полученные экспериментально профили. Суммирование производится по отсчетам дальности.

I P i exp ( P ^mod + C )

K = .                     =

V I ( P ^exp )2 I ( P ^mod + C )2

.

Поиск постоянной составляющей C , описывающей уровень шума (ионосферного и аппаратурного), производился исходя из условия максимума функционала (2) в виде условия (3), сводящегося к линейному уравнению на C (4):

^d-K = 0, dC

C =

^I P exp ^I ( p mod )2  ^^ p exp p mod ^^ p mod n I P exp P mod - I Pi exp I P mod

Диапазон значений высоты слоя с неоднородностями был выбран от 100 до 135 км, толщины – от 1 до 13 км и угловой чувствительности – от 2 до 27 дБ/град. При этом были рассчитаны профили при всех значениях параметров в указанном диапазоне с шагом 2.5 км для высоты, 3 км для толщины слоя; значения угловой чувствительности рассчитаны по геометрической прогрессии с шагом 30 %. Нижняя граница, равная 100 км, была выбрана из-за присутствия в рассеянном сигнале еще и сигналов некогерентного рассеяния, существенно ухудшающих точность определения параметров когерентного эха при высотах слоя ниже 100 км.

Для проверки устойчивости решения, в том числе и при наличии шумов, было проведено тестирование методики на устойчивость на всех значениях сетки. Тестирование проводилось путем наложения на профили аддитивных шумов, соответствующих как ионосферным шумам, так и статистическим шумам, связанным с конечностью времени накопления мощности. В ходе тестирования было использовано три вида шума по 500 реализаций:

• 1.    Шум с постоянной средней амплитудой, соответствующий ионосферному шуму. В этом случае амплитуда шума составляла 2 % от максимума профиля мощности.

• 2.    Шум с амплитудой, пропорциональной мощности сигнала, соответствующий статистическим шумам. Амплитуда шума – 4 % от текущего значения профиля мощности.

• 3.    Низкочастотный шум, соответствующий шумам, вносимым приемной аппаратурой. Амплитуда шума – 2 %.

На рис. 3 приведены графики распределения ошибок обращения при проведении тестирования. Из графиков видно, что наиболее устойчивыми параметрами являются высота слоя с неоднородностями и его толщина. В определении угловой чувствительности методика проявляет наименьшую стабильность при таком тестировании, но, несмотря на это, дает удовлетворительную точность (обращения с ошибками более одного шага сетки не превышают 2 % от общего числа испытаний). Наименьшую стабильность методика показала при наложении низкочастотных шумов.

Кроме проверки изложенной методики на устойчивость и точность обращения модельных профилей мощности в присутствии искусственного шума, проводилась аналогичная проверка на устойчивость и точность обращения на профилях мощности сигналов КЭ, полученных экспериментально на Иркутском радаре НР при наложении искусственных шумов. При этом точность инверсии определялась как мера отличия полученных параметров из искусственно-зашумленных экспериментальных профилей от параметров, полученных при инверсии экспериментальных профилей без дополнительного искусственного

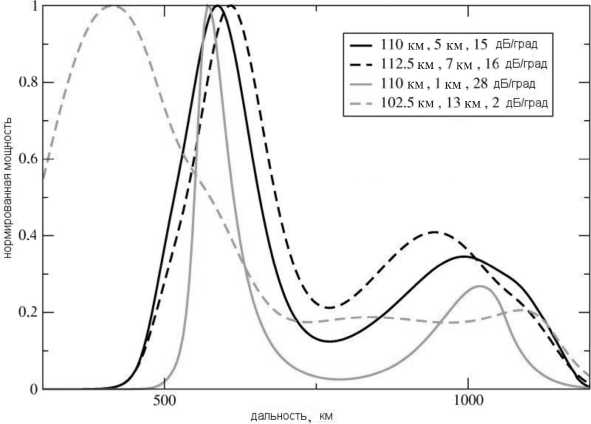
Рис . 2. Набор профилей , рассчитанных по модели , при различных значениях высоты слоя , толщины слоя и угловой чувствительности .

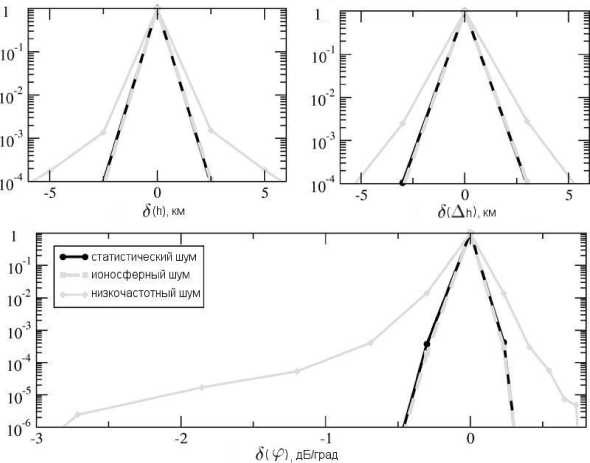
Рис . 3. Распределение ошибок обращаемых величин при тестировании методики на наборе модельных профилей . Серой сплошной линией на графиках отображено распределение ошибок при наложении низкочастотного шума с ам плитудой 2 %, черной штриховой – обращений с ионосферным шумом с амплитудой 2 % и серой пунктирной – стати стический шум накопления с амплитудой 4 %. На левом верхнем графике изображены ошибки при обращении высоты слоя ( шаг по высоте – 2.5 км ), на правом верхнем – ошибки при обращении его толщины ( шаг по толщине – 3 км ) и на нижнем графике – ошибки в определении угловой чувствительности ( шаг – 30 %).

зашумления. В ходе тестирования использовались аналогичные виды шумов. Картина, полученная в результате, несколько отличалась от полученной в модельном случае (рис. 4). Наиболее стабильными из обращаемых параметров при таком тестировании, как и в предыдущем случае, оказались высота слоя и его ширина. Менее стабильной показала себя угловая чувствительность, которая в ряде случаев определялась с неудовлетворительной точностью. В отличие от тестирования на сетке, тестирование на экспериментальных данных дало распределение ошибок, которое в значительной степени несимметрично, а также не всегда отвечает нашему критерию устойчивости. Такой эффект можно объяснить тем, что наблюдаемый экспериментально сигнал не всегда можно было ха- рактеризовать как КЭ либо условия экспери-мента существенно отличаются от модельных. Несмотря на это , количество ошибочно определяемых параметров (выходящих за пределы погрешности модели) достаточно мало , что позволяет предположить адекватность модели экспериментальным данным .

Влияние градиента электрического поля

Одним из наиболее серьезных отличий модельной ситуации от реального эксперимента является присутствие существенных градиентов электрического поля, которое в модельных расчетах мы полагаем однородным в исследуемой области. Как показало моделирование, учет градиента электрического поля оказывает сильное влияние на результаты тести-

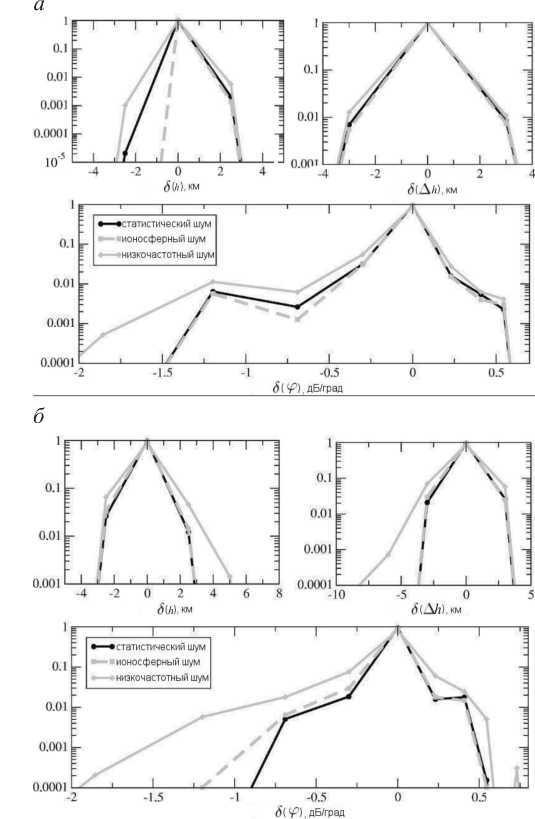
Рис . 4 . Распределение ошибок обращаемых величин при тестировании методики на экспериментальных данных за 25.09.1998 ( а ), за 16.07.2000 ( б ). Серой сплошной линией на графиках отображено распределение ошибок при наложе нии низкочастотного шума с амплитудой 2 %, черной – ионосферного шума с амплитудой 2 % и серой штриховой – статистического шума накопления с амплитудой 4 %. На левом верхнем графике изображены ошибки при обращении высоты слоя ( шаг по высоте – 2.5 км ), на правом верхнем – ошибки при обращении его толщины ( шаг по толщине – 3 км ), и на нижнем графике – ошибки в определении угловой чувствительности ( шаг – 30 %).

рования методики обращения. Поскольку электрическое поле входит в профиль мощности мультипликативным множителем, то в первом приближении наличие градиентов электрического поля можно описать умножением профиля мощности на линейную функцию со слабым наклоном, не отрицательную в области интересующих нас дальностей . Поэтому моделирование проводилось путем наложения на профили линейных градиентов и обращения полученных профилей с добавлением шума. Результаты тестирования показали , что присутствие линейного градиента электрического поля приводит к значительному увеличению дисперсии обращаемой величины, и при значении градиента электрического поля α = 4·10–3 км–1 в заданный интервал точности (2.5 км) укладывается ~70 % значений . Граничное значение градиента, выше которого методику можно считать неустойчивой, составляет α = 2·10–4 км–1. Кроме того, влияние градиента проявляется в возникновении систематической ошибки обращаемой величины в сторону повышения (рис. 5). На рис. 6 приведена зависимость математического ожидания обращенной высоты от значения градиента.

Из рисунка видно, что между этими величинами существует ярко выраженная линейная зависимость. Наклон регрессионной линии составляет ~655.19 км/(1/(км)). Это означает, что при характерных масштабах изменений электрического поля 655 км в определении высоты возникает ошибка ~1 км.

Принимая во внимание, что вследствие пространственного разрешения радара НР нет возможности точной калибровки профиля по дальности, методика не может абсолютно точно определять значения параметров, но допускает исследование их динамики. Поэтому можно предположить, что наибольшее влияние на ошибку определения параметров имеют не абсолютные величины градиентов, а их разброс в течение одного эксперимента. Действительно, как показало моделирование, оба эти эффекта (как увеличение дисперсии, так и появление систематической ошибки) могут быть в значительной мере сглажены, если рассмотреть влияние не самого градиента, а изменения градиентов от профиля к профилю на точность определения параметров. На рис. 7 показано распределение разности величин, полученных при

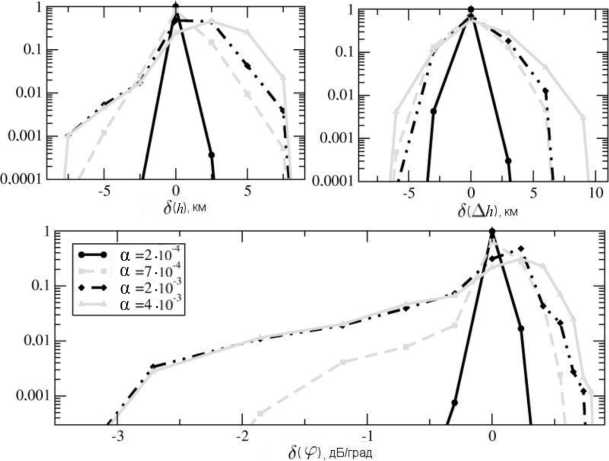
Рис . 5. Распределение ошибок обращаемых величин при тестировании методики с наложением линейных градиентов электрического поля . Различным линиям на графиках соответствуют распределения при наложении градиентов с раз личными амплитудами . На левом верхнем графике изображены ошибки при обращении высоты слоя , на правом верхнем – ошибки при обращении его толщины и на нижнем графике – ошибки в определении угловой чувствительности .

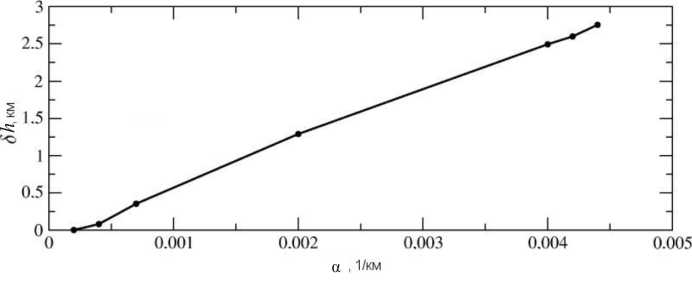
Рис . 6. Зависимость математического ожидания обращаемой высоты от значения градиента электрического поля .

обращении двух профилей с показателями градиента, разнесенными на α = 2·10–4 км–1. Из рисунка видно, что свойства обращения в значительной мере улучшаются по сравнению с учетом просто градиента, даже при больших абсолютных значениях α. Таким образом, если учитывать, что мы не можем обеспечить необходимую точность привязки профиля по дальности (порядка 10 км) для проанализированных экспериментов, то на относительные измерения параметров профиля (их временную динамику) влияние градиентов электрического поля становится достаточно слабым, если считать градиент почти постоянным в течение эксперимента.

Обсуждение полученных результатов

В ходе работы были обработаны данные, полученные на Иркутском радаре НР во время магнитных бурь 25– 26.09.1998 и 15–16.07.2000. Обработка данных выявила хорошее качественное согласование модели с экспериментальными данными (более половины обращенных модельных профилей совпадает с экспериментом с коэффициентом корреляции, превышающим 0.98, в 90 % случаев наблюдения когерентного эха коэффициент корреляции не ниже 0.94). На рис. 8 показаны результаты обработки экспериментальных данных за 25.09.1998 и 16.07.2000. Из графиков видно, что временной ход параметров слоя с неоднородностями (особенно высоты и толщины слоя) обладает хорошей преемственностью во времени и объясняет ряд особенностей временного хода накопленной мощности, что позволяет сделать вывод о корректности модели для описания экспериментальных данных.

Наблюдаемые быстрые вариации угловой чувствительности в зависимости от времени должны быть исследованы более детально, поскольку могут быть как увеличенной дисперсией ошибки, так и динамическими вариациями параметров. В частности, такое поведение может быть вызвано следующими причинами.

• 1.    Недостаточное временное разрешение экспериментальных данных (временное разрешение составляет ~4 мин), вследствие чего высокочастотная динамика изменения параметров приобретает шумоподобный вид.

  

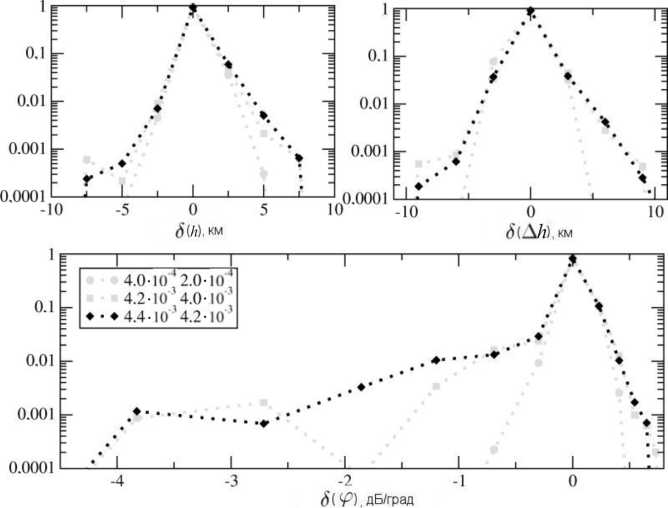
  Рис . 7. Распределение разности величин , полученных при обращении двух профилей , с показателями градиента , раз несенными на 2·10^–4 км ^–1.

  
  
  

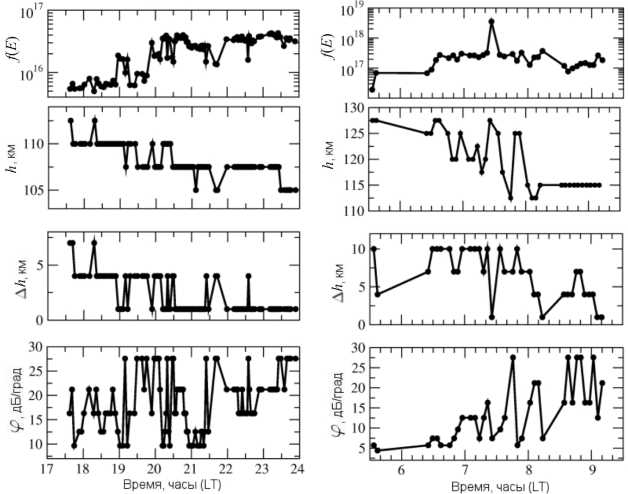
  Рис . 8. Результаты обработки экспериментальных данных за 25.09.1998 ( слева ) и 16.07.2000 ( справа ). Вверху пред ставлены графики временного хода множителя , определяемого величиной электрического поля , под ними – высоты слоя с неоднородностями , далее – толщины слоя , на нижних графиках представлен временной ход угловой чувствительности .

  
  

• 2.    Отсутствие учета широтного изменения параметров модели (в основном градиентов электрического поля), приводящее, как было показано ранее, к увеличению ошибок определения угловой чувствительности.

• 3.    Недоучет особенностей ДН радара на нижних лепестках (используемая модель не проходила калибровки в области нижних боковых лепестков , влияющих на форму профиля мощности), изменяющий саму модель и приводящий к дополнительным ошибкам в определении параметров.

• 4.    Отсутствие учета азимутальной ракурсной чув-

• ствительности неоднородностей (используемая модель рассеянного сигнала изотропна в плоскости, перпендикулярной магнитному полю, так как направление электрического поля нам известно только качественно), также изменяющее саму модель и приводящее к дополнительным ошибкам.

Заключение

В работе представлена методика определения параметров слоя рассеивающих неоднородностей, формирующих когерентное эхо, по данным Иркутского радара НР. Показано, что использованная методика обладает необходимой точностью (разрешение по высоте 2.5 км, по толщине слоя – 3 км и по угловой чувствительности неоднородностей – около 30 %). Обработка данных экспериментов 25–26.09.1998 и 15–16.07.2000 показала хорошее соответствие получаемых результатов с данными остальных исследователей: средняя высота слоя порядка 110–120 км, средняя толщина слоя – 5 км, средняя угловая чувствительность – около 15 дБ/градус [8].

Эксперименты с высоким временным разрешением позволили выявить временную зависимость определяемых параметров. Изменение толщины и высоты слоя от времени не противоречит другим данным, а временная зависимость угловой чувствительности неоднородностей от времени наблюдается впервые и требует дополнительных исследований.

Полученная методика обращения профилей мощности когерентного эхо позволяет проводить измерения параметров слоя неоднородностей, формирующих когерентное эхо, которые, в свою очередь, помогут проверить существующие модели формирования среднеширотного когерентного эха и косвенно исследовать поведение параметров нейтральной атмосферы на высотах E-слоя.