Определение поперечных размеров дефектов расслоения биметаллической пластины при активном тепловом неразрушающем контроле

Активный тепловой неразрушающий контроль является одним из перспективных методов выявления скрытых дефектов соединения слоев в изделиях из многослойных материалов [1]. При его проведении поверхность объекта нагревают или охлаждают с одной из сторон, а затем измеряют температуру на поверхности при помощи различных контактных или бесконтактных устройств (термодатчиков, пирометров, тепловизоров и др.). Если регистрация значений температуры производится со стороны нагрева, такую процедуру называют односторонней или «контролем на отражение», если с обратной – двухсторонней, или «контролем на прохождение» [1]. При наличии неоднородностей в материале (трещин, расслоений, пустот и др.) на соответствующих участках поверхности будет наблюдаться локальный перегрев или понижение температуры.

Одной из наиболее сложных задач является интерпретация полученных данных – определение типа дефекта и его параметров (поперечных размеров, глубины залегания и др.). Для ее решения используют математические модели и алгоритмы, учитывающие свойства объекта и технологические режимы контроля.

Особенностью исследуемых дефектов нарушения сплошности соединения слоев биметаллических пластин является то, что глубина нахождения дефекта известна, и основной задачей становится определение его размеров.

На термограммах экспериментальных образцов дефект создает видимый «отпечаток», образуемый точками с повышенной или пониженной температурой. Его размеры могут быть определены в пикселях с последующим переводом в традиционные метрические единицы. Однако при визуальной оценке погрешность может достигать 20 %, что является следствием увеличения температурного «отпечатка» при диффузии тепла в образце [1, 2].

Для более точной оценки применяют различные методы повышению информативности термографического изображения (усреднение, вычитание, деление изображений [3], наложение термограмм, полученных одновременно при односторонней и двусторонней процедуре контроля [4] и др.).

Помимо визуальной оценки определение размеров дефекта выполняют путем анализа профиля температуры на поверхности образца. Для этого набор значений температуры в отдельных точках поверхности преобразуют в графическое изображение температурного поля. Над дефектным участком полученный график функции температуры имеет характерный профиль с максимальной амплитудой в центральной точке дефекта.

В англоязычных источниках описан способ определения размера дефекта, обозначаемый аббревиатурой FWHM – Full Width Half Maximum [5, 6]. Ширина дефекта измеряется по положению проекции точки, соответствующей половине высоты максимального температурного перепада. Этот способ оценки дает приемлемые результаты, однако для некоторых материалов оценка размера дефекта получается заниженной [7, 8]. Описаны адекватные результаты определения размеров расслоений в углепластиковых композитных материалах [9, 10] и коррозии стальных пластин [5].

В.П. Вавилов и В.В. Ширяев показали, что координата экстремума производной функции температурного сигнала соответствует проекции границы внутреннего дефекта [11]. При этом точность определения размеров составляет до одного радиального шага пространственной сетки. Данный способ дает удовлетворительные результаты при определении размеров пор в алюминии и расслоений в пластиковых композитных материалах [1, 12, 13].

При определении поперечных размеров дефектов для более корректного расчета значений температурного сигнала над дефектом используют двух- и трехмерные модели теплового состояния объекта контроля, поскольку они учитывают тепловое рассеяние вокруг участка многослойного материала с внутренним дефектом.

Данная статья является продолжением исследования, описанного в работе [14], где была рассмотрена математическая модель теплового состояния многослойной пластины с дефектом соединения слоев и алгоритм решения краевой задачи теплового состояния с применением методов компьютерного моделирования. Целью исследования является анализ использования различных подходов к определению поперечного размера дефекта расслоения между металлами при активном тепловом неразрушающем контроле сталеалюминиевых пластин.

Материалы и методы

Рассмотрим трехслойную пластину (рис. 1) с наружными слоями из нержавеющей стали (1, толщиной h 1 ) и (3, толщиной h 3 ), между которыми расположен теплораспределительный слой из алюминия (2, толщиной h 2 ). Тепловой поток от источника нагрева q изл направлен по нормали к слоям.

Исследуются дефекты в виде воздушной прослойки в местах контакта наружных слоев изделия с внутренним теплораспределительным слоем с одной или другой его сторон. Размеры таких дефектов (диаметр d и толщина δ) существенно меньше размеров слоев пластины.

Процесс нагрева соответствует условиям проведения импульсного активного ТК. Для выявления дефектов с обеих сторон теплораспределительного слоя модель учитывает условия проведения односторонней и двусторонней процедур ТК.

Для обеспечения возможности определения поперечных размеров дефектов пластина рассматривается как симметричная относительно оси z в цилиндрической системе координат ( r , z ). Все слои пластины имеют форму цилиндра радиуса R , причем R » h i . Для температурного поля имеет место осевая симметрия ( dT/d ф = 0), считаем, что температурное поле нестационарное и двухмерное – T ( r , z , τ ).

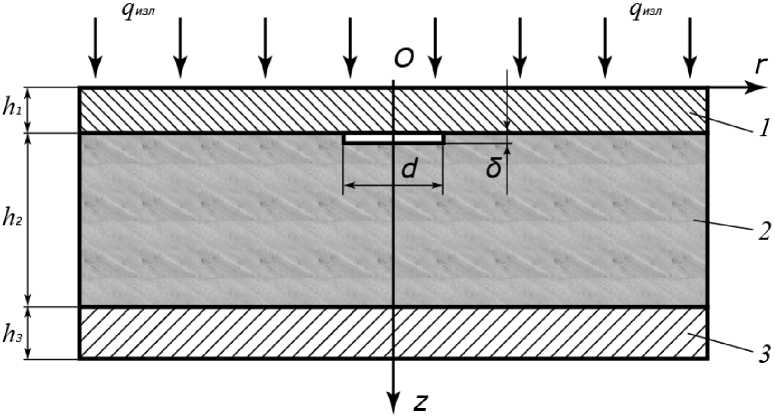
Рис. 1. Трехслойная пластина с цилиндрическим дефектом, ее основные размеры Fig. 1. Three-layer plate with a cylindrical delamination, its main dimensions

С учетом сформулированных допущений полагаем, что распределение температуры в исследуемой пластине описывается уравнением теплопроводности ( т >  0, 0 <  r <  R , 0 <  z <  ( h i + h 2 + h 3 )):

д T

—L = ai" дт i

( д ² T 1 д T д ² T ) — + -— + —"у

( д r ²    r д r    д z ² J

где i = 1, 2, 3 - номер слоя; т - время; T(r, z, т) - температура; ai = Xi /(ci -pi) - коэффициент температуропроводности; Xi, pi, ci - соответственно теплопроводность, плотность и удельная теплоемкость металлов.

Индекс 1 соответствует стальному слою при 0 < z < hi; индекс 2 - алюминиевому слою при h1 < z < (h1 + h2); индекс 3 - стальному слою при (h1 + h2) < z < (h1 + h2 + h3).

Подробное описание модели импульсного нагрева и последующего остывания многослойной пластины при наличии дефекта расслоения с учетом граничных условий и различных вариантов нагрева и охлаждения (односторонний и двухсторонний тепловой контроль) приведено в [14].

Определяются значения температуры Т на поверхности пластины и дифференциального температурного сигнала ∆Т , равного разности температур в исследуемой точке Т и в зоне, принятой за бездефектную, Т бд :

A T ( r , z , t ) = T ( r , z , t ) - T бд ( r , z , t ) . (2)

Для полученных функций распределения температуры и температурного сигнала вычисляются значения производных по формуле i _ 1 i+i   ч

д r     Ar

Оценка размера дефекта выполняется по положению точек, соответствующих проекциям экстремума производной и половины высоты амплитуды сигнала на ось r .

Численное моделирование и построение графиков выполняются с применением программного продукта GNU Octave (аналог MATLAB) [15].

Результаты

Рассмотрим решение задачи для различных режимов нагрева и времени наблюдения. Размеры пластины (см. рис. 1) h 1 = h 3 = 1,7 мм, h 2 = 5,6 мм, радиус пластин R = 50 мм, толщина воздушного зазора δ = 0,2 мм. Начальная температура пластины T 0 = 20 °С, температура окружающей среды t okr = 20 °С.

Теплофизические свойства стали: плотность ρст = 7850 кг/м3, удельная теплоемкость сст = = 504 Дж/(кг·К), коэффициент теплопроводности λст = 17 Вт/(м·К). Теплофизические свойства алюминия: плотность ρal = 2712 кг/м3, удельная теплоемкость сal = 897 Дж/(кг·К), коэффициент теплопроводности λal = 203,5 Вт/(м·К).

В различных вариантах решения диаметр воздушного зазора d принимается равным 5 и 10 мм, мощность теплового потока нагрева q изл составляет 10, 30 и 100 кВт/м².

Нагрев и измерение температуры выполняются со стороны дефекта. Время нагрева и шаг расчета выбираются в зависимости от величины мощности теплового потока.

На рис. 2 представлены графики распределения температуры по поверхности пластины со стороны дефекта при d = 5 мм, q изл = 100 кВт/м². Время нагрева τ 1 = 1 с, шаг расчета 0,01 c. Выполнены расчеты для времени наблюдения τ 1 = 1 с (после нагрева, график T 1 ) и τ 2 = 1,5 с (после охлаждения на воздухе, график T 2 ).

Определены точки, соответствующие половине высоты амплитуды изменения температуры A T /2 (после нагрева) и A T 2/2 (после охлаждения).

Также показаны графики производных функций распределения температуры S T /9r (после нагрева) и дT 2 /9r (после охлаждения).

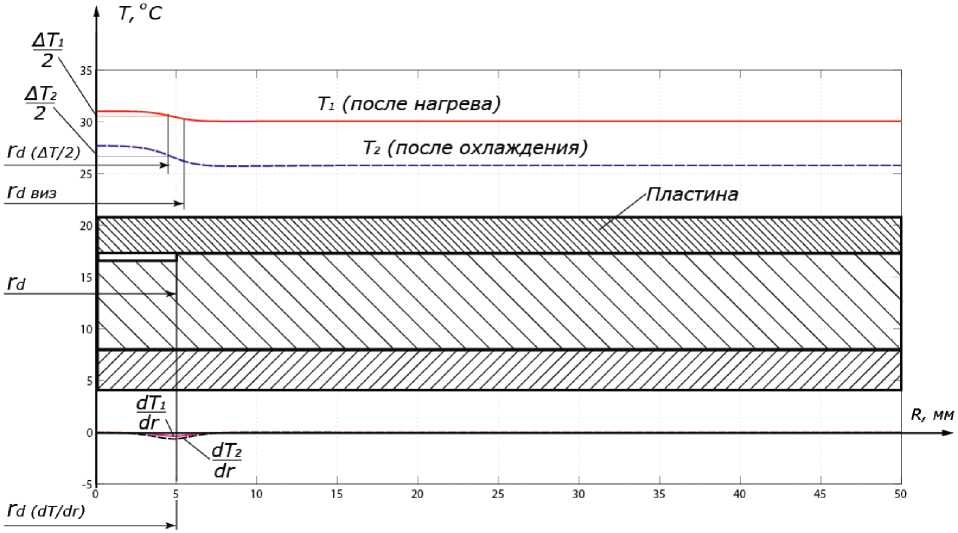
Рис. 2. Определение радиуса дефекта на основе анализа профиля температуры Fig. 2. Defect radius determined by analysing the temperature profile

Видно, что проекции экстремума производной r d ( д T / 9r ) точно соответствуют радиусу дефекта r_d как при наблюдении после нагрева, так и после охлаждения. В то же время радиус дефекта, определенный по проекции половины высоты амплитуды температуры r d ( A T /2 ) , меньше фактического размера дефекта в обоих случаях. При визуальной оценке радиус дефекта r _{d виз} превышает фактический.

На рис. 3 представлены графики распределения дифференциального температурного сигнала A T (после нагрева) и A T 2 (после охлаждения). При расчете значений температурного сигнала в качестве температуры бездефектной зоны используется значение T, в точке r = R . Построены графики производных функций температурного сигнала d ( A T 1 )/ д r (после нагрева) и d ( A T 2 )^ д r (после охлаждения), определены проекции характерных точек для оценки радиуса дефекта.

Оценки радиуса дефекта различными способами соответствуют оценкам, полученным при анализе профиля распределения температуры (см. рис. 2), но переход к дифференциальному температурному сигналу позволяет более наглядно представить результаты проведенных вычислений.

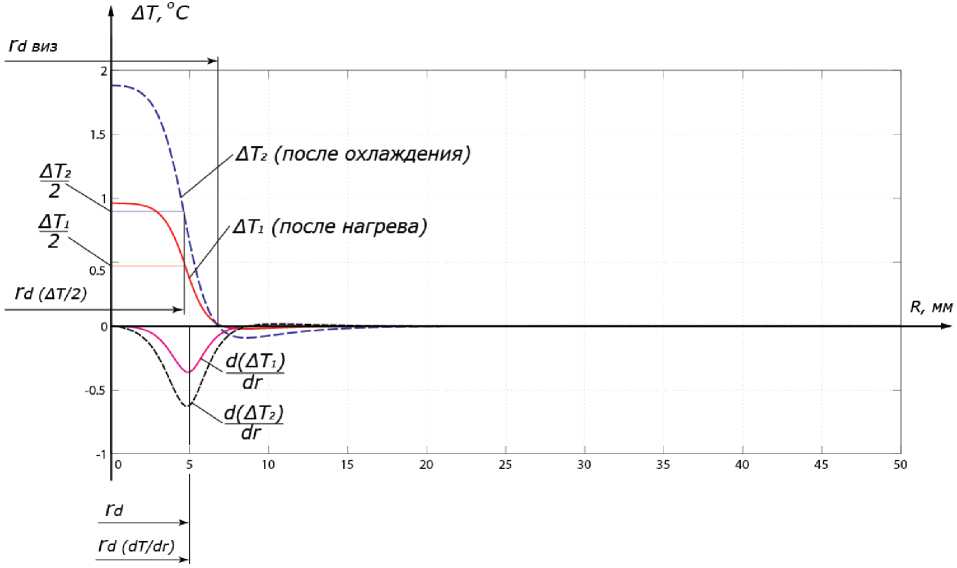
Рис. 3. Определение радиуса дефекта на основе анализа профиля дифференциального температурного сигнала

Fig. 3. Defect radius determined by analysing the differential temperature signal profile

В таблице представлены результаты моделирования теплового состояния для различных значений мощности теплового потока, времени нагрева и охлаждения.

Таблица

Результаты моделирования

Table

Simulation result

Тепловой поток, Вт/м2	Время нагрева, с	Время наблюдения, с	Шаг, с	r d , мм	( 8 T ) r      , мм d (d r J	( A T ) r       , мм d ( 2 J
10 000	30	30	0,1	5,0	5,0	4,75
	30	35	0,1	5,0	5,0	4,75
	30	45	0,1	5,0	5,0	4,75
	30	30	0,1	10,0	10,0	9,0
	30	35	0,1	10,0	10,0	8,75
	30	45	0,1	10,0	10,0	8,75
30 000	5	5	0,1	5,0	5,0	4,75
	5	10	0,1	5,0	5,0	4,75
	5	15	0,1	5,0	5,0	4,75
	5	5	0,1	10,0	10,0	9,25
	5	10	0,1	10,0	10,0	8,50
	5	15	0,1	10,0	10,0	8,25
	30	30	0,1	5,0	5,0	4,75
	30	35	0,1	5,0	5,0	4,75
	30	45	0,1	5,0	5,0	4,75
	30	30	0,1	10,0	10,0	9,0
	30	35	0,1	10,0	10,0	8,75
	30	45	0,1	10,0	10,0	8,75

Окончание таблицы

Table (end)

Тепловой поток, Вт/м2	Время нагрева, с	Время наблюдения, с	Шаг, с	r d , мм	(д T A r      , мм d (d r )	(A T A r       , мм d ( 2 )
100 000	1	1	0,01	5,0	5,0	4,75
	1	0,5	0,01	5,0	5,0	4,75
	1	6	0,01	5,0	5,0	4,5
	1	1	0,01	10,0	10,0	10,0
	1	0,5	0,01	10,0	10,0	10,0
	1	6	0,01	10,0	10,0	9,0
	2	2	0,01	5,0	5,0	5,0
	2	3	0,01	5,0	5,0	4,75
	2	10	0,01	5,0	5,0	4,75
	2	2	0,01	10,0	10,0	9,75
	2	3	0,01	10,0	10,0	9,5
	2	10	0,01	10,0	10,0	8,5

Анализ полученных данных позволяет сделать вывод, что оценка радиуса дефекта по проекции экстремума производной температуры и дифференциального температурного сигнала обеспечивает точное определение размера дефекта на используемой модели при различных параметрах режима нагрева.

Определение радиуса дефекта по проекции точки, соответствующей половине максимального температурного перепада, приводит к занижению размера дефекта. При малых временах наблюдения оценка более точная (отклонение в большинстве случаев не превышает одного радиального шага расчетной сетки), а при увеличении времени охлаждения величина отклонения растет.

Заключение

Результаты моделирования показывают, что использование проекции экстремума производной функции температурного сигнала позволяет точно оценить размер дефекта, а в случае с проекцией точки, соответствующей половине высоты амплитуды сигнала, оценка получается заниженной. Полученные данные в целом соответствуют результатам исследований для других видов материалов [5, 13] и могут быть использованы для дальнейших численных и экспериментальных исследований теплового состояния биметаллических пластин в процессе дефектоскопии методами активного теплового неразрушающего контроля.