Определение теплофизических характеристик и вязкостных свойств фаршевого сырья из прудового карпа

И. Ю. Алексанян, А. Х.-Х. Нугманов*, Н. В. Ярцева, Ю. С. Феклунова *Астраханский государственный технический университет, г. Астрахань, Россия; e-mail: , ORCID ID

e-mail: , ORCID ID

Консервация пищевых материалов растительного и животного происхождения низкими температурами всегда находила свое место среди других применяемых методов, способствующих продлению сроков хранения продовольственных товаров, и никогда не уходила из поля зрения технологов, инженеров и ученых, занимающихся проблемами сохранения продукции на длительный срок. Что касается непосредственно обработки сырья и полуфабрикатов, то основной вектор исследований направлен на увеличение интенсивности проводимых процессов, в частности процесса замораживания, при максимально возможном сохранении потребительских свойств конечного продукта. Эффективность применения низкотемпературного воздействия обусловлена заметным снижением биохимических и микробиологических превращений, происходящих в течение всего жизненного цикла обрабатываемого сырья, вследствие чего и наблюдается рост сроков хранения замороженной продукции при условии его правильной организации.

В последнее время инженерами-технологами разрабатываются перспективные способы получения гранулированного замороженного рыбного фарша с добавлением порошковых функциональных ингредиентов, путем применения технологии вакуумной заморозки ( Алексанян, 2018 ). Добавление сухих функциональных добавок в фарш способствует частичному связыванию влаги, тем самым снижая количество ее свободной части, которая и подвергается замораживанию, при этом снижаются затраты на заморозку. К тому же сами премиксы являются носителем ценных питательных веществ, которые в рыбе не содержатся, тем самым делая гранулированный рыбный фарш функциональным полуфабрикатом при сохранении требуемых к данному виду продукции потребительских свойств.

Несмотря на широкое разнообразие методов замораживания, к выбору способа и технических средств холодильной обработки различных пищевых материалов необходим индивидуальный подход. При этом его формирование обусловлено знаниями о физико-химических свойствах функционального рыбного фаршевого продукта, в частности теплофизических и реологических, которые необходимы для энергетических расчетов применяемой морозильной техники.

Учитывая, что рыба является идеальным сырьем для разработки пищевой продукции функционального назначения, есть веские основания предложить рыбный фарш в качестве основы для создания продуктов с пребиотическими свойствами. Следует отметить, что исследования, связанные с получением гранулированных рыбных фаршевых пищевых смесей, обогащенных пребиотической порошковой смесью "Лактулоза Премиум", на основе которых можно проектировать рецептурный состав новых рыбных кулинарных изделий, сбалансированных по биологической, пищевой и энергетической ценности, до сегодняшнего дня не проводились, что указывает на их актуальность.

В этой связи целью данного исследования является эмпирическое нахождение теплофизических характеристик (ТФХ) и вязкостных свойств разрабатываемого функционального рыбного фаршевого продукта, так как это важная составляющая теплотехнического расчета любого теплового оборудования, включая холодильное. Также знание коэффициентов переноса тепла необходимо и при решении математических моделей тепломассопереноса в различных применяемых технологиях замораживания.

Поставленная цель достижима при решении следующих задач:

• –    экспериментальным путем оценить величину физической плотности функционального фаршевого продукта как при положительных, так и отрицательных температурах его холодильного хранения;

• –    экспериментальным путем оценить величину динамической вязкости как условного коэффициента для функционального фаршевого продукта;

• –    экспериментальным путем оценить теплофизические характеристики функционального фаршевого продукта как при положительных, так и отрицательных температурах его холодильного хранения.

Материалы и методы

Обзор рыбоводно-биологических особенностей основных объектов прудового рыбоводства Астраханской области ( Ярцева, 2008 ) показал, что совместное выращивание товарного карпа и сеголетков щуки в прудах приносит двойную пользу: с одной стороны, хозяйство получает дополнительную продукцию за счет щуки, а с другой – повышается продуктивность основного объекта выращивания – карпа. Учитывая это, материалом для исследования служил разработанный мороженый фарш в виде мелких гранул из карпа и щуки в соотношении 70 : 30 с добавлением порошковой смеси "Лактулоза Премиум" (содержание активного вещества лактулозы в 6,6 г порошка составляет 5 г) и без нее ( ^ooshkam et al., 2018; Prat et al., 1990 ).

С целью обоснования рекомендованного содержания сухого премикса "Лактулоза Премиум" в рыбный фаршевый продукт из карпа и щуки, а также рационального соотношения между основными компонентами фарша, была проведена органолептическая оценка на соответствие готовых замороженных полуфабрикатов ГОСТ Р 55505-2013 ¹ ( Колаковский, 1991; Ярцева и др., 2010 ). По органолептическим показателям мороженый фарш должен соответствовать требованиям, указанным в табл. 1, согласно ( Колаковский, 1991 ).

Таблица 1. Органолептические показатели мороженого фарша Table 1. Organoleptic characteristics of frozen minced fish

Наименование показателя	Характеристика фарша из карпа с добавлением щуки
Внешний вид гранулы	Поверхность чистая, ровная цилиндрической формы. Допускаются небольшие впадины
Внешний вид фарша на срезе	Измельчение однородное, тонкое. Допускаются небольшие включения частиц кожи, пленки и пищевой добавки
Цвет	Cвойственный данному виду рыбы
Запах	Слабовыраженный, свойственный данному виду рыбы, без постороннего запаха. Допускается слабый запах ила, так как рыба прудовая
Консистенция	Плотная, упругая
Вкус после варки	Свойственный данному виду рыбы. Без неприятного привкуса. Без включения костей. Наличие сладковатого привкуса. Без привкуса добавки

Метод по определению плотности фаршевого материала в случае его замораживания

Величина физической плотности фаршевого полуфабриката ρ (кг/м ³ ) в температурном диапазоне от комнатной до криоскопической остается для инженерных расчетов практически постоянной величиной, в этом случае для определения ρ целесообразно применить пикнометрический способ, который широко известен и исчерпывающе описан в ГОСТ Р 53654.1-2009 (ИСО 2811-1:1997) ² ( Heiskanen, 1992; Зайдель, 2005; Кивилис, 1980 ).

Для интервала температур от –5 °С до криоскопической температуры значение ρ будет монотонно убывать по мере снижения температуры, так как оно определяется законами аддитивности, а в объекте появляется твердая фаза в виде льда ω, которую нельзя не учитывать и доля которой определяется из зависимости (1) для интервала температур t ∈ { t кр ; –5} ( Алексанян, 2018 )

ю = 100 - 154,926 • e ° ' ^365t , (1)

где t – температура объекта исследования, °С; t кр – криоскопическая температура исследуемой фаршевой смеси, равная –1,2 °С.

Пикнометрический метод измерения осуществляется путем погружения исследуемого образца, из которого путем вакуумирования удален воздух, в жидкую среду с заранее известной ρ. В качестве рабочей жидкости можно использовать очищенный керосин, так как он практически нерастворим в воде, являющейся важной составляющей исследуемого образца, и его характеристики хорошо известны. Для работы с исследуемым материалом и рабочей жидкой средой применяют соответствующий пикнометр – специальную колбу Рейшауэра, которая для определения ρ для сыпучих и твердых тел имеет тип ПТ и объем от одного до ста миллилитров. Для исследуемого материала рациональной можно считать вместимость колбы в диапазоне от 25 до 50 мл, так как потребуется минимум расходных материалов при достаточной точности необходимых измерений.

Принцип измерения плотности с помощью колбы Рейшауэра заключается в определении масс исследуемого образца в стеклянной емкости и пикнометра, заполненного жидкой рабочей средой, и по разности весов произвести расчет по формуле р =         ^.рж,

Р (т3-тп)-(т2-т1) жж где mn – масса сухого пикнометра, кг; m1 – масса исследуемого материала, кг; m2 – масса пикнометра с исследуемым материалом, кг; m3 – масса заполненного пикнометра, кг; ρж – плотность рабочей жидкости, кг/м3.

Таким образом, определив плотность образца по формуле (2) и проведя вычисления по ее изменению в зависимости от появления вымороженной влаги ω в материале при его замораживании (доля ω определяется из соотношения (1)), можно построить график, визуально показывающий изменение исследуемой характеристики в зависимости от температуры образца.

Метод по определению условного коэффициента эффективной динамической вязкости в объекте исследования

Выбирая между различными типами вискозиметров при изучении вязкостной реологии фаршевых полуфабрикатов сначала необходимо определиться между капиллярными и ротационными устройствами вследствие того, что теоретическая основа для исследования и расчета коэффициента динамической вязкости с их помощью максимально проработана. Но для случая исследования рыбных фаршей предпочтительнее ротационные вискозиметры, так как они требуют меньшее количество испытываемого материала для достижения необходимой вариативности скоростей сдвига.

Ротационная вискозиметрия для создания необходимых условий сдвига анализируемых материалов предусматривает расположение вязкой среды между двумя твердыми цилиндрическими элементами, именуемыми стакан и ротор, в специальном для этих целей устройстве, принципиальная схема которого представлена на рис. 1, при этом стакан связан с приводом, а ротор нет, он просто подвешен внутри стакана. Расстояние между ними должно быть минимизировано настолько, насколько это возможно, так как ротор должен осуществлять свое движение, контактируя с перемещающейся анализируемой средой, движение которой задает стакан. Минимально возможное расстояние регламентируется дисперсностью образца, и в нашем случае это степень измельчения фарша, а максимально возможное – когда вращательное движение у ротора визуально уже не наблюдается.

Внешняя оболочка, называемая стаканом, совершает круговое движение с постоянной угловой скоростью и передает второй оболочке – ротору – через движение исследуемой фаршевой среды свое вращательное движение. Таким образом, момент вращения роторной оболочки в системе "ротор – среда – стакан" является мерой вязкости среды. Принцип действия ротационного вискозиметра можно рассмотреть посредством его инверсной модели, представленной на рис. 1. Из рисунка видно, что изначально круговое движение реализует внешнее тело, а внутреннее, т. е. ротор, будет подвижным только в том случае, когда в отношении него сообщается угловой момент от исследуемой вязкой среды, находящейся между цилиндрическими телами.

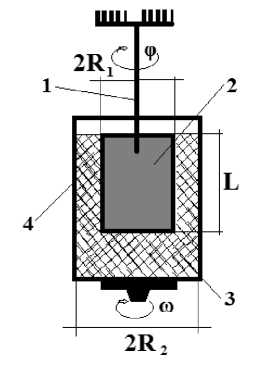
Рис. 1. Принципиальная схема работы ротационного вискозиметра:

1 – упругая нить; 2 – ротор; 3 – исследуемая пищевая среда; 4 – стакан Fig. 1. Schematic diagram of the operation of a rotational viscometer:

1 – elastic thread; 2 – rotor; 3 – test food medium; 4 – glass

На основе равенства крутящего момента рабочего органа M ₁ и вращающего момента инерции M ₂ определяют коэффициент динамической эффективной вязкости пищевых сред, являющейся прослойкой между ротором и стаканом.

Крутящий момент неподвижного ротора согласно схеме (рис. 1) уравновешивается силовым моментом, зависящим от упругих характеристик нити, на которую он и подвешен

^.R^

M ^ = 4nL_M^ ||,                           (3)

где M ₁ – момент, передаваемый через исследуемую среду; R ₁ и L – радиус и длина неподвижного ротора; ω – угловая скорость вращения внешней оболочки; R ₁ – радиус вращающейся оболочки вискозиметра; µ _э ф – динамическая вязкость исследуемой среды.

Вращающий момент инерции определяется из уравнения

M = nd ^ Gv                                           (4)

2       321 , где d, l – диаметр и длина нити; φ – угол, на который закручивается нить; G – момент упругости материала нити.

Учитывая, что M 1 = M 2 и после нескольких математических преобразований относительно µ эф имеем

_ _(fij-R|)nd^G^, .

Иэф   4nL(R2R)32lto’ или

Иэф = к ^

где k – константа ротационного вискозиметра.

Таким образом, определив константу ротационного вискозиметра для образца в ходе эксперимента, угол, на который закручивается неподвижно закрепленная нить, и постоянную угловую скорость внешней оболочки, можно рассчитать вязкость исследуемой среды или условный коэффициент эффективной динамической вязкости в объекте исследования.

Методика по определению теплофизических характеристик фаршевых материалов

В данном исследовании использовался зондовый метод, разработанный В. В. Красниковым с соавторами ( Красников и др., 1976; Панин и др., 1974 ) для вязких сыпучих, аморфных и жидких материалов, базирующийся на учете теплоинерционной способности применяемой термопары. Особенностью метода является простота установки и быстрота определения таких теплофизических характеристик, как теплопроводность Л , температуропроводность а и теплоемкость с _м исследуемого материала (Красников и др., 1976).

Эмпирический анализ применения этого метода показал ( Красников и др., 1976; Панин и др., 1974 ), что темп роста или падения температуры термопары θ ( _τ ) , мгновенно введенный в исследуемую среду, зависит от его характеристик, что в итоге и послужило основой для рекомендаций по его использованию. Отношение разностей температур или θ ( _τ ) определяется из выражения (7) ( Красников и др., 1976 ):

„   _ Т _с -Т ₂ ( _т )    2К rm exp(-u ² Fo)u ² du

^{( т )}      Т _с -Т ₀       п ^ о (и ² -К) ² +и ² К ^{2 ,}

„ Тс-Т2(т)   _                                  , где 6(Т) =----— — безразмерная температура; Fo — критерий Фурье; K = mc\pi — критерий, характеризующий

(т)     Тс-То        ■      ■            ■ “           ‘                              \ соотношение объемных исследуемого материала и термодатчика; m = ("уу2) — постоянная термодатчика, (м3·К)/Дж; c1ρ1 и c2ρ2 – объемная теплоемкость исследуемой среды и термодатчика, Дж/(м3·К).

Анализ исследований, проведенных авторами ( Красников и др., 1976 ), показывает, что по величине θ ( τ ) можно определить не только Л (Панин и др., 1974), но также а и с _м для вязких аморфных материалов, к которым относятся и фаршевые объекты. Для этого, применив известное разложение функциональной зависимости θ ( τ ) в ряд при значительных величинах аргумента Fo , можно получить следующее уравнение ( Красников и др., 1976 ):

9 ( т )

____1____ [

2КVП/Fo ³ +

1 , 3(2-К) _ 1 , 15[(К-2) ² -1] _ 1 , 2К Fo ⁺    4К ²       Fo ²

^1о 5 ^(К - ^{2)[(К-2) 2} - ^2] _ J_ ₊ ^ _{+ о)} 8К ³           Fo ³           ”

}•

Для остаточного члена Rn(Fo) огрешность δmax будет незначительная, принимаемая при замене ряда итоговой суммой, по абсолютному значению, которое меньше предыдущего, для пока не отброшенного члена ряда. В связи с этим, делая ограничения только по трем членам ряда, есть возможность получить уравнение, позволяющее определить критерии Fo и K, с погрешностью

⁰ 2 ( т )

1 2КVПVFo ³

(1+

3(2-К)

2К

1 + 15[(К-2) ² -1]   1 Т

Fo 4К ² Fo ² J

1 15[(К-2)²-1]    1 I

O _ma^x - |      4К 2      • f₀ 2 | .

Неравенство (10) как раз и показывает максимально возможное значение δ max .

Выражение (9) для 1 <  K < 2 в координатах у = 0 ₂(_т) ( Fo) VFo ³ и х = 1/ Fo является параболической функцией, имеющей экстремум при определенном значении Fo max . что подтверждается исследованиями различных материалов в источнике ( Красников и др., 1976 ).

Из необходимого условия экстремума функции (9) получим

Fo

⁰ 2(т)

VF0 ³ =

1    (2-К)К

5 [(К-2) ² -1] ,

1   |"0.15(2-К) ²

2КТп L (К-2) ² -1

Если, проведя необходимые опытные исследования, представить полученный результат в виде графической зависимости 0VT ³ = / (^ можно определить 0 _max . Затем из уравнения

θ

max

-

(2-К)К I ³ =    1 Г0.15(2-К)²

54(K-2) ² -1]J      2KVn (К-2) ² -1

11 -

полученного из соотношений (11) и (12), можно определить величину K и далее из (12) вычислить Fo _max , соответствующий критерию K .

Суммируя вышесказанное, можно утверждать, что разработанный В. В. Красниковым, А. С. Паниным и В. Д. Скверчаком метод ( Красников и др., 1976 ) является пригодным для определения всего спектра теплофизических свойств у исследуемого фаршевого объекта по значениям Fo max и K в момент τ max при достижении θ max . Окончательные расчетные формулы имеют следующий вид

• _ ^Fo max ^ ². а =-------;

  
  

  ^- max

_ К ^с м ^р м = “ ^;

• ^   Fo max ^ ² • К

  ^- max ^m ’

где R – эквивалентный радиус зонда, м.

Для проведения экспериментальных исследований по нахождению теплофизических характеристик фаршевых материалов по вышеописанному методу использовался электронный термометр "ЛТ-300", чувствительный элемент которого выполнен в виде небольшого тонкого зонда и отличается достаточной для проведения эксперимента прочностью, стабильностью физико-химических характеристик и хорошей воспроизводимостью температурных измерений. Ниже на рис. 2 представлена схема опытной установки.

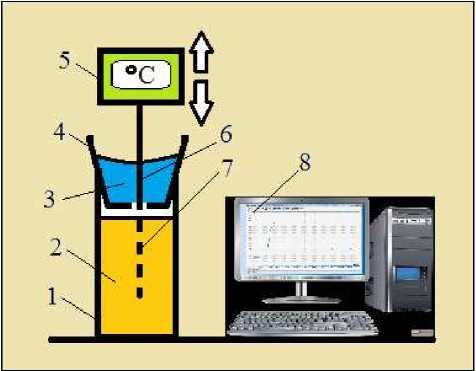
Рис. 2. Схема опытной установки: 1 – стакан для образца; 2 – исследуемый материал с комнатной температурой; 3 – смесь воды со льдом; 4 – стакан из бумаги; 5 – ЛТ-300;

6 – измерительный зонд в начальном положении; 7 – измерительный зонд в конечном положении;

8 – ЭВМ с программой ThermoChart

Fig. 2. The experimental setup: 1 – glass for the studied material; 2 – material having room temperature; 3 – ice water to maintain a low temperature close to 0 °C; 4 – paper cup; 5 – LT-300; 6 – probe measuring in the initial position; 7 – probe measuring in the final position; 8 – computers with ThermoChart program

Порядок проведения эксперимента следующий. Экспериментальная установка собирается согласно схеме (рис. 2). В бумажный стакан загружается смесь воды и льда, которая обеспечит заданный интервал температуры в районе 1–2 °С внутри емкости, где устанавливается измерительный зонд электронного термометра "ЛТ-300". С помощью программы ThermoChart, температурные значения, определяемые используемым термометром, фиксируются на мониторе ЭВМ. В стакан для образца помещается изучаемый фаршевый продукт, имеющий комнатную температуру, после чего согласно схеме (рис. 2) бумажный стакан помещается поверх него. Когда все подготовлено для проведения эксперимента, исследователь должен максимально быстро пробить зондом дно бумажного стакана для попадания термопары в фаршевую смесь. Термопара, попав в объект с комнатной температурой из среды с нулевой, начинает нагреваться, тем самым давая нужные эмпирические значения, фиксируемые ЭВМ.

Эксперимент повторяется не менее пяти раз, данные сводятся в таблицу, и согласно приведенной методике производится расчет необходимых теплофизических характеристик для объекта исследования.

ТФХ рыбных полуфабрикатов в интервале температур от криоскопической до 20 °С остаются для инженерных расчетов практически постоянной величиной, следовательно, для этого диапазона достаточно провести эксперименты по их нахождению для объектов исследования методом, подробно описанным выше.

Для интервала температур от –5 °С до криоскопической зависимость ТФХ от средней температуры образца будет определяться аддитивно только для теплоемкости материала, так как остальные характеристики не подчиняются правилу аддитивности. В интервале от –5 °С до криоскопической температуры величина удельной теплоемкости в продукте меняется в связи с появлением вымороженной влаги ω, доля которой определяется из зависимости (1). Что касается двух остальных теплофизических характеристик, то их величина также меняется в связи с появлением вымороженной влаги, но это изменение возможно определить только экспериментально. Следует отметить, что зависимость коэффициента температуропроводности от температуры рыбного фарша при его замораживании можно описать и математически, используя наработки, представленные в источнике ( Алексанян, 2018 ).

Согласно (Алексанян, 2018), зависимость коэффициента температуропроводности в продукте a от температуры объекта исследования в интервале от –5 °С до криоскопической для рыбных фаршей можно описать экспоненциальной зависимостью a •IO7 = 25- a! • cb<

где t – температура объекта исследования, °С; a ₁ и b ₁ – численные коэффициенты.

Численные коэффициенты a ₁ и b ₁ в уравнении (17) определяются при решении системы из двух равенств

( 25 - a _Y • e ^{b l t kp} = а кр 125 - й ! • e ^{b l t k0H} = а кон ^,

где t кр – криоскопическая температура для объекта исследования, °С (–1,2 °С); t кон – нижний предел температуры замораживания, °С (задается); a кон – величина коэффициента температуропроводности в продукте при температуре t кон , м ² /с (определяется экспериментально); a кр – величина коэффициента температуропроводности в продукте при температуре t кр , м ² /с (определяется экспериментально).

Таким образом:

• –    решив систему уравнений (18) можно получить уравнение, по которому графически или аналитически легко определить величину коэффициента температуропроводности в продукте при выбранной для него отрицательной температуре в интервале от криоскопической до заданной;

• –    определив теплоемкость образца по формуле (15) и проведя вычисления по ее изменению с учетом появления вымороженной влаги ω в материале при его замораживании (доля ω определяется из уравнения (1)), можно построить график, визуально показывающий изменение исследуемой характеристики в зависимости от температуры образца;

• –    зная зависимость плотности исследуемого материала от его температуры в области замораживания по известному уравнению λ = ac _M ρ _M , можно получить соотношение, по которому графически или аналитически легко определить величину коэффициента теплопроводности в продукте при выбранной для него отрицательной температуре в интервале от криоскопической до заданной.

В результате появляется возможность определить весь необходимый для инженерных расчетов комплекс теплофизических характеристик для исследуемых материалов в заданном интервале отрицательных температур.

Результаты и обсуждение

Физическая плотность фаршевых полуфабрикатов из щуки и карпа без и с добавлением пребиотика при положительных температурах от криоскопической до 20 °С практически не изменяется, поэтому для этого интервала ее можно определить методом пикнометрии, описанным выше.

Для интервала температур от –5 °С до криоскопической точки значение ρ будет монотонно убывать по мере снижения температуры, так как оно определяется законами аддитивности, а в объекте появляется твердая фаза в виде льда ω, которую нельзя не учитывать и доля которой определяется из зависимости (1).

В табл. 2 для исследуемых материалов дано эмпирически полученное среднее значение ρ (кг/м ³ ) в нужном интервале температур.

Таблица 2. Усредненное значение ρ ср (кг/м ³ ) для рыбных фаршей в интервале температуры t ср Table 2. Average density ρ (kg/m ³ ) for minced fish in the temperature range t ср

Наименование	ρ ср (кг/м 3 ) для t кр ≤ t ср ≤ 5
Фарш из щуки и карпа без добавки	≈ 925
Фарш из щуки и карпа с добавкой	≈ 940

Для практического удобства, когда необходимо рассчитать плотность рыбных фаршей ρ см при отрицательных температурах, целесообразно использовать аддитивную зависимость (19), в которой ω определяется из (1) от требуемой температуры

_         1

Рсм = WM |W(i-j20)| T-W, Рл^ЮО     Рвл      Рсух. ост где W – доля влаги в рыбном фарше, кг/кг; ω – процент вымерзшей влаги в фарше, %; ρл, ρвл и ρсух. ост – плотность соответственно льда, воды и сухого остатка, кг/м3.

Если физическая плотность воды в разных агрегатных состояниях является известной величиной, то плотность сухого остатка фарша может быть вычислена следующим образом:

W сух. ост рсух. ост     1 W ,                                                    (20)

рсм рвл где wсух. ост – доля сухого остатка в продукте, кг/кг; ρсм – плотность рыбных фаршей, кг/м3; ρвл – плотность воды, кг/м3.

Основным объектом исследования является фарш из щуки и карпа с пребиотической добавкой, для которого плотность сухого остатка ρ сух. ост , вычисленного по формуле (20), равна

0,28           кг рсуХ. ост =       0,72 = 814 м?

940 - 1000

Плотность рыбного фарша ρ см , обогащенного пребиотиком "Лактулоза Премиум", при отрицательных температурах описывается уравнением (21), в котором to определяется из зависимости (1) от требуемой температуры

Р см = (7,85 • 10 -⁶ «(t) + 7,2 (1 - ^1^ ) • 10 "⁴ + 3,44 • 10 "⁴ ) "¹ .                   (21)

На рис. 3 представлена графическая интерпретация зависимости плотности ρ рыбного фаршевого полуфабриката из щуки и карпа от его средней температуры t .

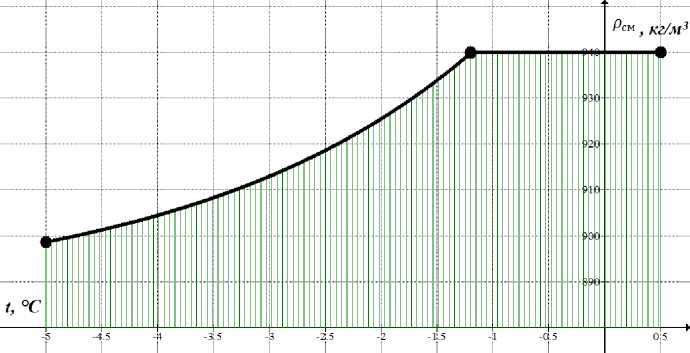
Рис. 3. Зависимость физической плотности фарша от его средней температуры Fig. 3. The dependence of the physical density of minced meat on its average temperature

Из анализа кривой (рис. 3) видно, что по мере повышения температуры плотность фарша монотонно повышается и достигает величины 940 кг/м ³ при достижении криоскопической температуры в исследуемом материале, после чего значение рассматриваемой характеристики остается практически постоянной до 10 °С.

Реологическое понятие вязкости является важнейшим для изучения структурно-механических свойств пищевых материалов, вследствие его противодействия пластическому сдвиговому течению ( Косой и др., 2005; Коган и др., 1990 ), которое считается практически постоянным. В связи с этим динамическая вязкость может считаться мерой интенсивности внутренних сил трения материала, противодействующих его плоскопараллельному сдвиговому течению. С точки зрения энергетической составляющей механизма противодействия она уже является мерой рассеивания теплоты, получаемой при преобразовании механической энергии в тепловую при движении жидкости.

Многие пищевые среды не подчиняются закону вязкости жидкости, и их меру сопротивления сдвиговому течению уже нельзя описать одним параметром – коэффициентом вязкости, поэтому приходится такие системы описывать с помощью реологических многокритериальных уравнений. Такие системы называются неньютоновскими или "аномальными", хотя для пищевых дисперсных сред именно ньютоновское поведение более аномальное, чем неньютоновское. Вязкостные свойства неньютоновских жидкостей можно характеризовать условным коэффициентом динамической эффективной вязкости.

Для исследования вязкостных свойств рыбных фаршей с пребиотической добавкой и без использовался вискозиметр РВ-8 с рифленым ротором (шаг рифления 2 мм). У ротора радиус R ₁ = 0,013 м, а радиус стакана R 2 = 0,019 м. Результаты проведенных измерений при пятикратном повторении приведены в табл. 3.

Таблица 3. Среднее значение коэффициента динамической эффективной вязкости µ эф (Па·с) исследуемых рыбных фаршей

Table 3. Average value of dynamic effective viscosity coefficient µ эф (Pa·s) of minced fish

Наименование	µ эф , Па·с
Фарш из щуки и карпа без добавки	≈ 690
Фарш из щуки и карпа с добавкой	≈ 890

Полученные данные не идут в разрез с литературными ( Алексанян, 2018; Дряхлов и др., 2012), что говорит об их адекватности и возможности применения в инженерных расчетах. Следует отметить, что по сравнению с вязкостными характеристиками фарша с добавкой величина коэффициента динамической вязкости фарша без добавки меньше, это обусловлено его большей пластичностью из-за более высокого содержания в нем жира, что влияет на снижение силы внутреннего трения.

ТФХ рыбного полуфабриката в интервале температур от криоскопической до 20 °С остаются постоянными, поэтому для этого диапазона достаточно провести эксперименты по нахождению значений коэффициента теплопроводности λ (Вт/(м·К)), температуропроводности a (м ² /с) и удельной теплоемкости c _M (Дж/(кг·К) для фарша из щуки и карпа с добавлением пребиотика, подробно описанным ранее зондовым экспресс-методом ( Красников и др., 1976; Панин и др., 1974 ).

В результате проведенных экспериментальных исследований по нахождению ТФХ фаршевого образца с заданным составом и температурой выше криоскопической, при их пятикратной повторности, были получены данные, с использованием которых, согласно методике ( Красников и др., 1976; Панин и др., 1974 ), производился расчет необходимых характеристик. В итоге для рыбного фарша при его влажности 72 % были получены значения искомых величин, представленные в табл. 4.

Таблица 4. Результаты по экспериментальному определению ТФХ рыбного фарша Table 4. The results of the experimental determination of the TPH of minced fish

Влажность W , %	Удельная теплоемкость c M , Дж/(кг·К)	Температуропроводность a ⋅ 10 7 , м 2 /с	Коэффициент теплопроводности, λ, Вт/(м·К)
≈ 72	≈ 3 652	≈ 3,11	≈ 1,07

В связи с тем что применяемая методика предназначена для материалов, куда свободно и быстро можно поместить зонд термодатчика, определение ТФХ для фаршевых смесей при отрицательных температурах является затруднительным. Поэтому выявление зависимостей ТФХ исследуемого фарша в интервале температур от –5 °С до криоскопической целесообразно провести расчетным путем, основываясь на анализе подобных фаршевых систем при тех же прочих равных условиях ( Алексанян, 2018 ).

Для практического удобства, когда необходимо рассчитать cM рыбных фаршей при температурах ниже криоскопической, целесообразно применить правило аддитивности и в итоге получить уравнение (22), в котором величина ω определяется из зависимости (1) от требуемой температуры см = — Сл + ^fl- — )свл + (1- ^)ccvx ост,                    (22)

^ ЮО л V. 100/ вл              * сух. ост,                                   \ / где W – доля влаги в рыбном фарше, кг/кг; ω – количество вымерзшей влаги в фарше, %; cл, cвл и cсух. ост – удельная теплоемкость соответственно льда, воды и сухого остатка, Дж/(кг·К).

Если теплоемкость льда и воды является известной величиной, то теплоемкость сухого остатка фарша может быть вычислена следующим образом:

сух . ост

См-^С вл

W       , сух. ост

где wсух. ост – доля сухого остатка в продукте, кг/кг; cM – теплоемкость рыбного фарша, Дж/(кг·К); cвл – теплоемкость воды, Дж/(кг·К).

Основным объектом исследования является фарш из щуки и карпа с пребиотической добавкой, для которого теплоемкость сухого остатка с сух . ост , вычисленного по формуле (23), равна

3652 - 0,72 ∙ 4183

= 2287 ( кДЖк )

^{С су}х . ^ост =        028

Теплоемкость рыбного фарша cM, обогащенного пребиотиком "Лактулоза Премиум" при температурах от –5 °С до криоскопической, описывается уравнением (24), преобразованном из уравнения (22), в котором количество вымерзшей влаги ω определяется из зависимости (1) от требуемой температуры см = 14,59to(t) + 3011,76 (1 - ^) + 640,36.

На рис. 4 представлена графическая интерпретация зависимости теплоемкости c M рыбного фаршевого полуфабриката с функциональной добавкой из прудовых карпа и щуки от его средней температуры t .

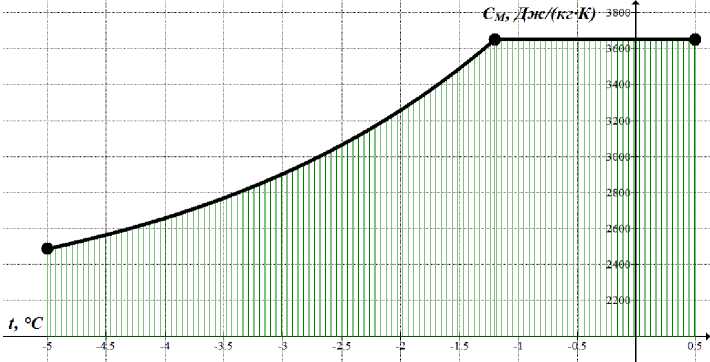
Рис. 4. Зависимость теплоемкости фарша от его средней температуры

Fig. 4. The dependence of the heat capacity of minced meat on its average temperature

Для практического удобства, когда необходимо рассчитать величину a рыбных фаршей при температурах ниже криоскопической, целесообразно использовать уравнение (17), в котором необходимо определить численные коэффициенты a ₁ и b ₁ .

Численные коэффициенты a ₁ и b ₁ в соотношении (17) определяются решением системы из двух уравнений (18), но для ее решения остается неизвестной величина a _кон , которая может быть найдена только опытным путем. Значение a _кон , как показывает практика, для рыбных фаршевых систем при их температуре –5 °С разнится в пределах ±3 % ( Алексанян, 2018 ) и в среднем составляет ≈ 22 ⋅ 10 ^–7 м ² /с, поэтому целесообразнее принять величину a _кон = 22 ⋅ 10 ^–7 м ² /с без проведения эмпирических исследований, ведь погрешность в 3 % может быть вполне допустима для инженерных расчетов.

Тогда для исследуемой фаршевой смеси система уравнений (18) будет выглядеть следующим образом:

125 - а ₁ • е ⁶¹"¹ ’ ² = 3,11 ( 25 - а ₁ • е ^ь1~⁵ = 22

Решение данного уравнения в среде MathCad дает следующие результаты:

41,003

Fmd⁽a i , Ь ^) = ( ₀ 523 /

В этом случае зависимость коэффициента температуропроводности для исследуемого фарша a от его температуры t в интервале от –5 °С до криоскопической можно описать следующей экспоненциальной зависимостью а •Ю7 = 25 -41,003 • e°’523t.

На рис. 5 представлена графическая интерпретация зависимости коэффициента температуропроводности a рыбного фаршевого полуфабриката с функциональной добавкой из прудовых карпа и щуки от его средней температуры t .

Коэффициент теплопроводности фаршевого полуфабриката функциональной направленности λ (Вт/(м·К)) для заданного интервала температур определяется через соотношение: а = —-—, где зависимости a(t), cM(t) СмРсм и ρсм(t) уже известны, при этом на участке, где значения ТФХ постоянны, для нахождения λ достаточно просто перемножить характеристики a, cM и ρсм.

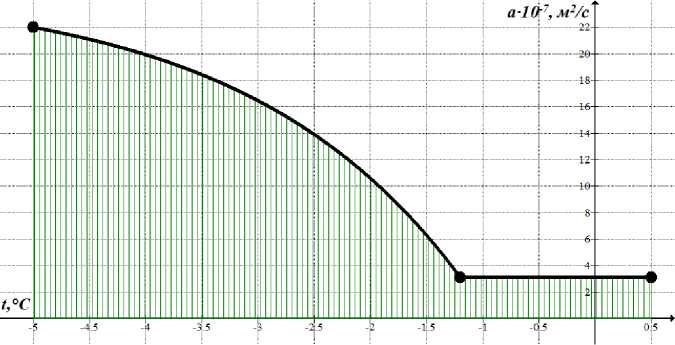
Рис. 5. Зависимость коэффициента температуропроводности фарша от его средней температуры

Fig. 5. The dependence of the thermal diffusivity of minced meat on its average temperature

На рис. 6 представлена графическая интерпретация зависимости коэффициента теплопроводности λ рыбного фаршевого полуфабриката с функциональной добавкой из прудовых карпа и щуки от его средней температуры t .

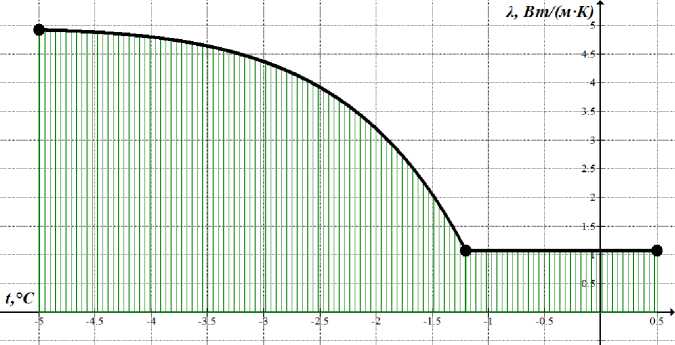
Рис. 6. Зависимость коэффициента теплопроводности фарша от его средней температуры

Fig. 6. The dependence of the coefficient of thermal conductivity of minced meat on its average temperature

Полученные результаты не противоречат литературным данным ( Алексанян, 2018; Лысова и др., 2004 ), что свидетельствует об их адекватности и возможности применения в инженерных расчетах. Из полученных графиков видно, что теплофизические характеристики объекта исследования, как и всех пищевых продуктов, существенно зависят от температуры при ее снижении ниже криоскопической и образовании вымороженной влаги. Следует отметить, что штриховка на графиках проведена для лучшей их наглядности без какого-либо физического смысла.

Заключение

Путем экспериментального определения физико-химических характеристик, определенных в задачах исследования для разрабатываемого функционального рыбного фаршевого продукта, можно заключить, что цель данного исследования достигнута, а именно:

• –    получены значения физической плотности функционального фаршевого продукта (табл. 2, рис. 3) и коэффициента условной динамической вязкости (табл. 3);

• –    определены теплофизические характеристики функционального фаршевого продукта (табл. 4, рис. 4–6);

• –    полученные результаты не противоречат литературным данным, что свидетельствует об их адекватности и возможности применения в инженерных расчетах.

Таким образом, использование полученных результатов вкупе с другими необходимыми исследованиями позволит выявить рациональные режимные параметры для технологии рыбного гранулированного мороженого фарша функциональной направленности, близкие к оптимальным. В итоге это обеспечит целостность и стабильность технологического потока, которые напрямую влияют на увеличение производительности, снижение энергоемкости применяемых в технологии процессов и улучшение качества получаемого в итоге конечного продукта.