Определение времени и скорости нагрева измельченных плодов яблок при терморадиационной сушке

Введение. Большая часть сельскохозяйственных продуктов является высоковлажными телами, что вызывает порчу продуктов вследствие жизнедеятельности различных микроорганизмов в вод- ной среде. Поэтому большинство пищевых продуктов подвергают сушке, в процессе которой их влажность значительно уменьшается [1].

Одним из прогрессивных способов нагрева, создающим значительный ресурсосберегающий эффект, является ИК-нагрев, применяемый для сушки сельскохозяйственных продуктов.

Для правильного понимания механизма процесса сушки и для его расчета необходимо знание тепло- и массообменных характеристик материалов и степени их влияния на время и скорость нагрева до установившейся температуры.

Цель исследования : определение времени и скорости нагрева до установившейся температуры измельченных плодов яблок при ИК-сушке.

Методы и результаты исследования . Расчет значений времени и скорости нагрева необходимо начать на основе совместного решения уравнений теплового баланса и теплопередачи с учетом динамики нагрева.

Процессы нагрева по своей природе являются динамическими, связанными с изменением теплосодержания нагреваемых материалов и явлениями теплопередачи, которые не могут происходить мгновенно.

Рассмотрим систему «излучатель - материал» как простейший случай нагрева однородного и изотропного материала.

Уравнение теплового баланса за промежуток времени dT имеет вид dQ i = dQ 2 + dQ з, (1)

где dQ i - количество теплоты, подведенное к материалу за время d T , Дж; dQ 2 - количество теплоты, поглощенное в объеме материала, Дж; dQ 3 - потери теплоты в окружающую среду, Дж.

После подстановки значений отдельных составляющих в уравнение теплового баланса (1) уравнение предстанет в развернутом виде следующим образом [2, 3]:

AEF о d r = Мс d r + q_mrF d T + а( t - t в ) F d T , (2)

где А - поглощательная способность материала; E - поверхностная плотность потока от излучателей, Вт/м2; Fо - площадь облучаемой поверхности материала, м2; М - масса облучаемого материала, кг; с - удельная теплоемкость облучаемого материала, Дж/(кгК); dt - изменение температуры материала, °С; qm - начальная интенсивность или скорость испарения вещества, кг/(м2ю); r - удель- ная теплота испарения, Дж/кг; F – площадь полной поверхности материала, м2; α = αк + αи – суммарный коэффициент теплоотдачи, Вт/(м2·К); αк – коэффициент теплоотдачи конвекцией, Вт/(м2·К); αи – коэффициент теплоотдачи излучением Вт/(м2·К); t и tв – температура материала и окружающего воздуха, °С, или

С учетом обозначений уравнение (3) представлено в следующем виде:

^Тн~Г ⁺ t ^- t у = 0- d τ

Это дифференциальное уравнение порядка, решение которого

первого

Мс dt      (    AEF_a  qj' A

---+ 1 -\ t в +-----о- - m²² - 1 = 0.        (3) a F d т    (     a F    a J

τ

T

Tн t tначe

+ t у ¹ -

e

— A Г T .

,

\

J

Введем обозначения [2, 3]:

Т = —, н    _{α F}

^F = F ^,

AE qr     AE - qmrF tv = tB +—- — = tB +---^--, у   в  αF   α    в      αF

где Тн – постоянная времени нагрева, с; F – отношение площадей полной поверхности и облучаемой ее части; tу – установившаяся температу- dt ра материала (при — = 0). dт где tнач – температура материала в начальный момент времени при т = 0, °С.

Примем значение температуры материала в начале нагрева t нач = 15 °С.

Из зависимости (6), представляющей собой уравнение нагрева однородного материала, видно, что рост температуры материала по мере ИК-энергоподвода подчиняется экспоненциальной зависимости (рис.). При т ^ °° или практически (с погрешностью не более 5 %) для т > (3+4) Т н устанавливается баланс между количеством теплоты, поглощаемым материалом, и тепловыми потерями в окружающую среду. Этому моменту соответствует установившаяся температура нагреваемого материала, при этом t = (0,95÷0,98) t у .

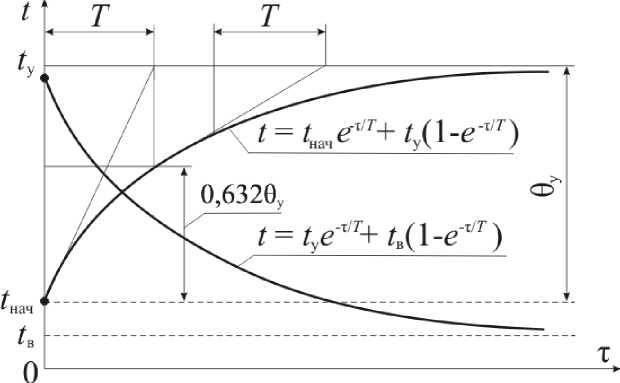
Кривые нагрева и охлаждения однородного тела

На практике кривые нагрева незначительно могут отличаться от приведенных на рисунке в силу тех упрощений, которые были приняты в исследовании. Однако общий принцип динамики нагрева и характеризующие его параметры остаются неизменными.

Выражение, полученное из уравнения (6), для определения времени нагрева материала до любой температуры t в промежутке от t нач до t у выглядит следующим образом:

т = T ln -’-нач. (7) ^- у ^- t

Скорость нагрева в процессе подводы теплоты к материалу определяется по выражению

t — t нач

T

T _н

dt dr

T       . T .

н 1- e Т н

На основе полученных уравнений в [1–3] видно, что к числу важнейших параметров при тепловой обработке относится постоянная времени нагрева Т н , определяющая значение скорости нагрева.

Физический смысл постоянной времени нагрева раскрывается следующим определением. Постоянная времени нагрева определяется как такое время, в течение которого температура материала достигла бы установившейся температуры, если бы не было тепловых потерь в окружающую среду (адиабатный процесс). Как видно из рисунка, при значении α = 0 температура тела изменяется во времени по прямой. Из чего следует, что постоянная времени нагрева не зависит от мощности, подводимой к материалу, а зависит только от условий отвода теплоты (охлаждения).

По вышеизложенной методике нами был произведен расчет постоянной времени нагрева, времени нагрева и скорости нагрева для измельченных плодов яблок, подвергаемых ИК-сушке. Выбор в качестве объекта исследования плодов яблок исходил из соображений того, что яблоки являются незаменимым продуктом питания и сырьем для перерабатывающей промышленности [4–10]. Кроме этого, выбор был обусловлен тем, что яблони среди плодовых растений наиболее популярны и получили очень большое распространение в России, занимая значительную площадь от общей площади плодовых насаждений, в том числе имеют большие перспективы и потенциал при выращивании их в Южном Предбайка-лье [11, 12].

Опыта тепловой обработки данного продукта в стране и мире достаточно, но тем не менее исследования по определению оптимальных режимов термообработки пищевых продуктов всегда остаются актуальными.

Если принять М = V ρ ( V – объем материала, м³; ρ – его плотность, кг/м³), то выражение (4) можно записать следующим образом:

T =

н

Мс α F

с ρ V α F ^.

Как видно из выражения (9), для расчета постоянной времени нагрева необходимы сведения по удельной теплоемкости, плотности, об объеме и площади полной поверхности материала, а также суммарном коэффициенте теплоотдачи в окружающую среду.

Для практических условий П.Д. Лебедев значение суммарного коэффициента теплоотдачи α рекомендует принимать в пределах от 18,6 до 23,2 Вт/(м2·К) [2]. В настоящих расчетах принято значение α = 20 Вт/(м2·К).

По [13] предложить надежную формулу для определения физической плотности яблок при сушке не представляется возможным. Физическая плотность разных сортов яблок не одинакова, поскольку яблоки различаются химическим составом и пористостью. Физическая плотность яблок, выращенных в России, находится в пределах от 660 до 860 кг/м3 [14]. Примем для расчетов ориентировочно среднее значение плотности яблок ρ = 760 кг/м3.

На практике плотность плодов яблок и коэффициент теплоотдачи в окружающую среду при сушке меняются, но для приблизительных расчетов значение плотности и коэффициента теплоотдачи решено принять постоянным на всем протяжении процесса влагоудаления.

Необходимые сведения по удельной теплоемкости плодов яблок в зависимости от температуры и массовой доли влаги нами получены по формуле, заимствованной из обстоятельной работы по теплофизическим характеристикам пищевых продуктов А.С. Гинзбурга и М.А. Громова [13, 15]:

с = 4187 – 3526 n + 3,6 Тn , (10)

где n – массовая доля сухого вещества.

Формула (10) справедлива в широком интервале Т и ω , и она рекомендуется авторами для практического использования. Температура для сушки яблок t = 70 °C ( T = 343 К).

Форма плодов яблок, нарезанных на промышленной овощерезке, имеет вид параллелепипеда. Минимальный размер составляет 25×3×3 мм, максимальный – 40×6×6 мм.

Как известно, в процессе сушки большинство материалов уменьшается в размерах, изменяет форму, т. е. дает усадку, что необходимо учитывать при расчетах. Овощи и плоды относятся к числу коллоидных капиллярно-пористых материалов и при сушке дают значительную усадку, уменьшаясь в объеме в 3-4 раза.

Усадка по объему и площади полной поверхности материала пищевых растительных материалов имеет линейную зависимость от влагосо-держания [14, 16]:

V = V 0 (1 + β v u ),               (11)

F = F с.в. (1 + β F u ),               (12)

где V 0 – объем абсолютно сухого тела для материалов, имеющих усадку на протяжении всего процесса сушки или в период падающей скорости, м³; β v – коэффициент объемной усадки (относительное изменение объема тела при изменении влагосодержания на 1 кг/кг, или на 1 %); u – вла-госодержание материала, кг влаги на кг с.в.); F с.в. – площадь абсолютно сухого материала, м²; β F – коэффициент усадки по площади.

Коллектив авторов [14] при расчетах продолжительности сушки пищевых растительных мате- риалов влиянием усадки рекомендует пренебречь, аргументируя это следующим. При сушке в неподвижном слое в испарении участвуют только частицы, поверхность которых смочена. Усадка, сокращая поверхность частиц, одновременно способствует увеличению пористости слоя, т. е. повышению поверхности смачивания. Эта взаимная компенсация явлений, происходящих при усадке, исключает ее влияние на процесс сушки.

Нами же при вычислении постоянной времени соотношение V принято постоянным на всем F протяжении процесса влагоудаления из предположения того, что при усадке объем и площадь полной поверхности материала уменьшаются равномерно одинаково.

Подставив в формулу (9) значения удельной теплоемкости, объема и площади полной поверхности материала, получим:

т =

н

ср V _ р(4187 - 3526n + 3,6Tn) V0 (1 + вvu)

a F              a            F^, (1 + вfu)’

Объем и площадь полной поверхности измельченных плодов яблок определены по известным в геометрии формулам. Числовое значение соотношения ^V для плодов яблок с размерами F

25×3×3 мм составило 0,708·10-3 м, а для плодов яблок с размерами 40×6×6 мм – 1,395·10-3 м.

Данные общих расчетов сведены в таблицу.

Постоянная времени нагрева измельченных плодов яблок

№ п/п	Массовая доля влаги ω , %	Удельная теплоемкость с , Дж/(кг·К)	Постоянная времени нагрева Т , с	Время нагрева т ~ 3 T ,c	Скорость нагрева dt/ d r , °С/с
1	80	3728,76	100,25–197,71	300,76–593,13	0,18–0,09
2	70	3499,64	62,73–123,71	188,19–371,12	0,29–0,15
3	60	3270,52	43,97–86,71	131,9–260,12	0,42–0,21
4	50	3041,40	32,71–64,71	98,13–193,52	0,56–0,28
5	40	2812,28	25,20–49,71	75,61–149,12	0,73–0,37
6	30	2583,16	19,84–39,13	59,53–117,40	0,92–0,47
7	20	2354,04	15,82–31,20	47,47–93,61	1,16–0,59
8	10	2124,92	12,70–25,04	38,09–75,11	1,44–0,73

Анализируя данные таблицы, можно сказать о существенном влиянии на время и скорость нагрева значений содержания влаги. С уменьшением влаги в материале с 80 до 10 %, а в свою очередь – удельной теплоемкости, время нагрева до установившейся температуры резко уменьшается, а скорость нагрева увеличивается. Также скорость и продолжительность нагрева при одном и том же влагосодержании в значительной мере определяются толщиной плодов яблок. Так, при увеличении толщины от 3 до 6 мм продолжительность процесса нагрева увеличивается в 2 раза.

Выводы. Данные расчетов позволяют сделать вывод, что сушку плодов яблок необходимо вести с понижением ИК-энергоподвода. В начале сушки при высокой влажности яблоки можно без ущерба для их питательных веществ подвергать длительному и мощному облучению, а по мере уменьшения влажности интенсивность ИК-энергоподвода необходимо постепенно снижать. Это дополнительно обусловлено тем, что при высокой влажности сухое вещество яблок более термостойко и опасаться перегрева в начале сушки не стоит.