Оптимальная адаптивная система для исследования зарядовых и частотных свойств гетероструктур с зарядовой связью

ОПТИМАЛЬНАЯ АДАПТИВНАЯ СИСТЕМА ДЛЯ ИССЛЕДОВАНИЯ ЗАРЯДОВЫХ И ЧАСТОТНЫХ СВОЙСТВ ГЕТЕРОСТРУКТУР С ЗАРЯДОВОЙ СВЯЗЬЮ

В.П. Заярный, И.Н. Пономарев, С.В. Гирич, О.А. Астафурова

Разработана система для исследования зарядовых и частотных характеристик твердотельных гетероструктур в составе приборов с зарядовой связью и особенностей взаимодействия носителей заряда в слоях гетероструктур с внешними полями радиочастотного диапазона. Оптимизация измерительных цепей системы производилась на основе требований проводимых экспериментов.

В работах лауреата Нобелевской премии академика Ж.И. Алферова [1, 2] особо подчеркивается, что зарядовые свойства гетероструктур, обусловленные взаимодействием носителей заряда с внешними полями, определяются чистотой твердотельных слоев (материалов), входящих в их состав и качеством границ раздела между ними.

Для гетероструктур типа «металл – поликремний – диэлектрик – полупроводник», применяемых, в частности, для получения приборов с зарядовой связью, наличие примесей в слое диэлектрика, в сочетании с технологическим процессом, обусловливает присутствие подвижной компоненты встроенного заряда Q_d ^п . Наличие нарушений кристаллической структуры диэлектрика является причиной появления диполей, обусловливающих наличие неподвижной компоненты встроенного заряда Q_d ^н . У всех реальных гетероструктур в их слоях имеют место моноэнергетичес-кие уровни с энергией активации E_t , определяющие порядок кинетики m и частотные факторы ω происходящих на них зарядовых процессов. Наличие поверхностных состояний в запрещенной зоне полупроводника является следствием деструкции его кристаллической решетки вблизи границы раздела «диэлектрик-полупроводник» (Д-П) и определяется распределением плотности поверхностных состояний по ширине запрещенной зоны N_ss ( Е ).

Таким образом, для описываемых гетероструктур основными характеристиками, определяющими их зарядовое состояние, являются Qd = Qdп+ Qdн, Nss(E), Еt, m и ω. Известно [3], что частотные факторы для зарядовых процессов, определяемых диполями и перемещением ионов в диэлектрике, имеют значения не более 103 Гц, и поэтому в радиочастотном диапазоне на частотные свойства гетероструктур влияния практически не оказывают. Поверхностные состояния вблизи границы раздела Д-П сказываются на частотах до единиц мегагерц. Частотные факторы для зарядовых процессов, определяемых наличием моноэнергетических уровней (МУ) полупроводника вблизи границы раздела Д-П, могут достигать значений порядка 1012Гц, и именно они определяют высокочастотные свойства гетероструктур в составе приборов с зарядовой связью (ПЗС).

Анализ методов определения указанных зарядовых характеристик показал, что наиболее информативными из них, позволяющими обеспечить выполнение указанных требований, являются методы емкостной и термоактивационной спектроскопии. Одними из наиболее информативных методов емкостной спектроскопии являются методы высокочастотных (ВЧ) и низкочастотных (НЧ) вольт-фарадных характеристик (ВФХ), изотермической релаксации емкости (ИРЕ). Известно, что методы ВЧ и НЧ ВФХ позволяют с методической погрешностью не хуже 10 % определить N_ss ( Е ) и Q_d , однако совсем не позволяют определять Е_t и соотношение подвижной и неподвижной компонент Q_d . Метод ИРЕ позволяет наиболее точно (с методической погрешностью порядка 1 %) определять Е_t одного МУ. Однако он не позволяет определять несколько Е_t (имеют место у некачественных гетероструктур) и совершенно нечувствителен к наличию поверхностных состояний. Те характеристики, которые невозможно определить указанными методами ( E_t для нескольких моноэнергетических уровней, их порядок кинетики и частотные факторы), позволяют получить методы термоактивационной спектроскопии.

Анализ термоактивационных методов исследования гетероструктур позволил выделить следующие из них как наиболее информативные: методы термостимулированных токов поляризации (ТСП), термостимулированных токов деполяризации (ТСД) и метод термостимулированного тока с фракционным нагревом (ФТСТ). В [3] численным моделированием показано, что метод ТСП дает минимальную методическую погрешность при определении Q_d ^п и Q_d ^н (до 15 %). Метод ТСД с термоочисткой от фонового заряда дает минимальную методическую погрешность (порядка 1 %) при определении Е_t и температурного положения максимумов пиков T_m . Метод ФТСТ позволяет определять распределение N_ss ( E ) с методической погрешностью порядка 10 %, что больше, чем в случае НЧ ВФХ. Поэтому этот метод использовался только в целях взаимопроверки.

Из сказанного следует, что современный эксперимент по исследованию зарядовых процессов в гетероструктурах имеет следующие особенности. Необходимость очистки границ раздела слоев гетероструктур от фонового заряда при выявлении в них дефектов требует максимальной адаптивности системы к изменяющимся условиям текущего эксперимента. Поскольку зарядовые процессы в гетероструктурах очень слабые, то система должна иметь предельно достижимую разрешающую способность и точность измерений. Наличие быстропротекающих процессов требует от них максимального быстродействия. Кроме того, решение подобных задач связано с реализацией нескольких смежных методов определения зарядовых характеристик гетероструктур, анализом и сопоставлением полученных результатов измерений и выводом заключений, что требует создания экспертных систем.

В [4] была решена задача формирования моделей функциональных модулей (ФМ) в составе избыточного функционального ресурса (ИФР) для синтеза оптимальных, адаптивных систем, а также разработана основа для их оптимизации. Синтез конкретной системы для исследования зарядовых и частотных свойств гетероструктур и ПЗС на их основе предполагает конкретизацию моделей и вывод требуемых оптимальных измерительных структур системы. Приводимые модели содержат операторы преобразования R (∙). В скобках указывается выражение, описывающее преобразование, выполняемое данным ФМ [4], основные характеристики данного ФМ, алгоритм комбинирования ФМ в измерительной структуре, обязательное отсутствие (abs) или наличие (inc) ФМ, необходимых для работы данного ФМ.

Так, имеющиеся в составе ИФР первичные измерительные преобразователи (ПИП) для реализации методов изотермической релаксации емкости, высокочастотных и низкочастотных вольт-фарадных характеристик, термостимулированных токов поляризации и деполяризации, будут иметь следующие модели:

М51ВЧВФХ = (RslO, (s1 E [S imin, S 1max],fs1 E f 1min,fs imax] )si, (u 1(t) E [U1min = 0 В, U1max = +1 B], f. E [fIrmin = 10-3 Гц, f,rmaX= 1 Гц]), abs 0, inc М-1 s 1ВЧВФХ);

Мs2НЧВФХ = (Rs2(*X (s2 E [S2min, S2max],fs2 E fs2min,fs2max] )s2, (u2(t) E [U2min = 0 B, U2max = +1 B], f2 E [f2rmin = 10 Гц,f2rmax = 1 Гц]), abs 0, inc М s2НЧВФХ);

Мs3ИРЕ = (Rsз("), (s3 E [S3min; S3max],fs3 ^ 0,25 МГц )s3, (Ui(t) E [U3min = -10 В, U3max = 0 В], fi = 0,25 МГц), abs 0, inc М-1 sзире);

Мs4ТСП = (Rs4(*), (s4 E [S4min, S4max], fs4 E [fs4min, fs4max] )s4, (u4(t) E [U4min = -1 В, U4max = +1 В], f4 E [f4rmin = 10-2 Гц, f.max = 10 Гц]), abs 0, inc М-1 s4ТСп)

Мs5ТСД = (Rs5("), (s5 E [S5min, S5max], fs5 E [fs5min, fs5max] )s5, (u5(t) E [ U5min 1 В, U5max = +1 В], f 5 E [fimln = 10-2Гц, f irmax = 10 Гц]), abs 0, inc М-1 s5ТСД).

При реализации термоактивационных методов использовалась также термопара:

Мs6Т/П = (Rs6(-), (s6 E [S6min, S6max],fs6 E [fs6mn,fs6max] )s6, (Uб(1) E [U6mn = 0 В, U6max = +10 мВ], f, E [firmin = 10-2Гц, f ™ = 1 Гц]), abs 0, inc М-1 s6т/п), а емкостных – генератор напряжения для обеспечения требуемых режимов гетероструктур;

Мs7Vg = (Rs7(-), (Us7(t) E [U7min = -10 В, U7max = +10 В],fs E [f ,mm = 10-3 Гц, f 'max = 10-2 Гц]), abs 0, inc М-1 s7Vg).

У всех использовавшихся ПИП варианты их перебора отсутствовали, их характеристики нерегулируемые, поэтому их оптимизация не проводилась.

Как показано в [4], из свойств используемого ИФР следует, что оптимизация измерительных структур в данном случае возможна только в части аналого-цифрового преобразователя (АЦП), устройства сопряжения (УС) и цифровой фильтрации (ЦФ). Из анализа требований данного эксперимента, согласно правилам оптимизации [4], из имеющихся АЦП наименьшей дисперсией погрешности, а следовательно, оптимальным в данном случае является АЦП, имеющий наибольшее количество разрядов q _{2 max} = 16 и f_{max 2} = 1,0 МГц, описываемый моделью:

М ацП = М аЦП2 = ( R АЦП2 ( - ), (( U E [ U 2min = - 5 В; U 2max = +5 В], f E [0, f max2 = 1,0 МГц]), М уВХ ,

М ком ) ацп2 , q 2max = 10 ^ 16, abs (М ацп1 , М ацпз , М ацп4 , М ацш ) inc 0).

Согласно тем же критериям оптимизации, оптимальным в данном случае является устройство сопряжения (УС) АЦП с ЭВМ, имеющее наименьшее время задержки ( t _зус1 = 0,1мкс) и описываемое моделью:

М ус = М ус1 = ( R уст ( - ), (М ацп2 ) ус1 , q уст = 24, t зус1 = 0,1 мкс, abs М ус2 , inc 0).

Цифровая фильтрация в организуемых экспериментах не проводилась.

Имея полученную выше информацию, определим нерегулируемые характеристики остальных ФМ, которые оптимизации не подлежат. После каждого ПИП следуют нормализаторы, коэффициенты передачи которых ( К_U ) с минимальной методической погрешностью определяются по полученным диапазонам выходных сигналов ПИП и диапазону входного сигнала АЦП. Для них:

М _ш = ( R Н1 ( - ), ( 5 1, м 5 1 ) Н1 , К и 1 = 0,5, abs 0, inc М ^{- 1} Н1 );

М н2 = ( R Н2 ( - ), ( 5 2, М 5 2 ) Н2 , К и 2 = 5, abs 0, inc М ^{- 1}н2 );

М нз = ( R нз ( * ), ( 5 3, М 5 3 ) Н3 , К и 3 = 0,5, abs 0, inc М ^{- 1}нз );

М Н4 = ( R Н4 ( - ), ( 5 4, М 5 4 ) Н4 , К и 4 = 5, abs 0, inc М — 1Н4 );

М Н5 = ( R Н5 ( - ), ( 5 5, м 5 5 ) Н5 , К и 5 = 5, abs 0, inc М — 1Н5 );

М Н6 = ( R Нб ( - ), ( 5 6, М 5 6 ) Н6 , К и 6 = 5, abs 0, inc М ^{- 1} нб );

М Н7 = ( R Н7 ( - ), ( 5 7, М 5 7 ) Н7 , К и 7 = 500, abs 0, inc М^нт ).

Индексы у обозначений нормализаторов и УВХ являются одноименными с индексами соответствующих ПИП.

Для УВХ основной характеристикой является время хранения ( t_хр ). Учитывая быстродействие выбранного АЦП ( t_пр = 1 мкс) и тот факт, что опрос каналов производится последовательно, модели УВХ для соответствующих каналов будут иметь вид:

М увх1 = ( R УВХ1 ( - ), ( и е [ U AЦПmiп , U АЦПmax ] ) уВХ1 , t хр1 = 1 МКС, abs 0, inc 0);

М увх2 = ( R увх2 ( - ), ( и е [ U Ацпmin , U Ацпmax ] ) Увх2 , t хр2 = 2 мкс, abs 0, inc 0);

М увхз = ( R увхз ( - ), ( и е [ U Aцпmiп , U Ацпmax ] ) Увхз , t хр3 = 3 мкс, abs 0, inc 0);

М увх4 = ( R увх4 ( - ), ( и е [ U Ацпmin , U Ацпmax ] ) увх4 , t хр4 = 4 мкс, abs 0, inc 0);

М увх5 = ( R увх5 ( * ), ( и е [ U Ацпmin , U Ацпmax ] ) увх5 , t хр5 = 5 мкс, abs 0, inc 0);

М увх6 = ( R увх6 ( - ), ( и е [ U Ацпmin , U Ацпmax ] ) увх6 , t хр6 = 6 мкс, abs 0, inc 0);

М увх7 = ( R УВХ7 ( " ), ( и е [ U АЦПmin , U АЦПmax ] ) УвХ7 , t хр7 = 7 мкс, abs 0, inc 0).

Согласно алгоритму комбинирования, у многоканальной системы, при использовании одного АЦП, на его входе должен быть аналоговый коммутатор (АК). Его основной характеристикой является количество аналоговых входов. В нашем случае оно определено и имеет значение n _АК2 = 8, а модель данного АК будет иметь вид:

М ак = М аК2 = ( R АК2 ( - ), ( и е [ и АЦПш1п , U АЦПmax ], М увх ) АК2 , n АК2 = 8, abs М аК1 , inc 0).

Поскольку количество каналов n = 7, а n _АК2 = 8, то, для уменьшения наводок и мультипликативной составляющей погрешности, неиспользуемый вход АК соединяется с общим проводом.

После ввода цифровой информации с выхода АЦП в ЭВМ производятся операции, обратные нормализации ( R ^–1 _Н ) и первичному измерительному преобразованию ( R ^–1 _s ), а модели соответствующих преобразований будут следующими:

М ^{- 1} Н1 = ( R ^{- 1} Н10 , (М ацп , М ус , М цф ) ^{- 1} Н1 , ( Ки 1) ^{- 1} abs 0, inc 0);

М 1Н2 = ( R 1Н2 ( ^- ), (М ацп , М ус , М цф ) 1Н2 , ( Ки 2) ¹ abs 0, inc 0);

М 1нз = ( R 'нз0 , (М ацп , М ус , М цф ) ¹ нз , ( Ки 3) ¹ abs 0, inc 0);

М ^{- 1} Н4 = ( R "шС), (М ацп , М ус , М цф ) ^- 1Н4 , ( Ки 4) ^{- 1} abs 0, inc 0);

М ^{- 1} Н5 = ( R -шС), (М ацп , М ус , М цф ) ^- 1Н5 , ( Ки 5) " ¹ abs 0, inc 0);

М ^{- 1} Н6 = ( R -*№(•), (М ацп , М ус , М цф ) ^{- 1} Н6 , ( Ки 6) ^{- 1} abs 0, inc 0);

М ^{- 1} Н7 = ( R -'шО, (М ацп , М ус , М цф ) ^{- 1} Н7 , ( Ки 7) ^{- 1} abs 0, inc 0);

М ^{- 1} s 1 = ( R ^{- 1} s 1 (^), (M ^{- 1}hi )_; 1 ^{- 1}, abs 0, inc 0);

М ^{- 1} s 2 = ( R ^{- 1} s 2 <^), (М ^{- 1} Н2 )_; 2 ^{- 1}, abs 0, inc 0);

М ^{- 1} s з = ( R ^{- 1} s зО , (М ^{- 1}нз )_; 3 ^{- 1}, abs 0, inc 0);

М ^{- 1} s 4 = ( R ^{- 1} s 4 <^>, (М ^{- 1} Н4 )_; 4 ^{- 1}, abs 0, inc 0);

М ^{- 1} s 5 = ( R ^{- 1} s 5 (^), (М ^{- 1} Н5 )_; 5 ^{- 1}, abs 0, inc 0);

М ^{- 1} s 6 = ( R ^{- 1} s 60 , (М ^{- 1} Н6 )_;6 ^{- 1}, abs 0, inc 0);

М ^{- 1} s 7 = ( R ^{- 1} s 7 (^), (М ^{- 1} Н7 )_; 7 ^{- 1}, abs 0, inc 0).

Специализированное математическое обеспечение (СМО) производит обработку вводимых массивов информации и получение искомых характеристик гетероструктур:

[ Et ] ИРЕ = F 1 [ uс ( t )];

[ Qd , Nss ( E )] ВЧ ВФХ = F 2 [ С гет ( Vg ), Vg ( t )];

[ Qd , Nss ( E )] НЧ ВФХ = F 3 [ I гет ( Vg ), Cd , V пз ];

[ Eti , mi , т] тсд = F 4 ^[ I тсд⁽ T , T ⁽ t )];

[ Qd ^п, Qd ^н] ТСП = F 5 [ I ТСП ( T ), T ( t )].

Здесь u_с ( t ) – график изотермической релаксации емкости; С _гет ( V_g ) и V_g ( t ) – зависимость емкости гетероструктуры от напряжения, определяющего ее режим, и зависимость этого напряжения от времени; I _ТСП ( T ), I _ТСД ( T ), T ( t ) – зависимость термостимулированных токов поляризации и деполяризации от температуры и температуры от времени; F ₁ – F ₅ – соответствующие расчетные формулы (они известны из литературных данных). Для всех расчетных соотношений также известны значения их методических погрешностей ( п ), значения которых (в процентах) вносятся в модели соответствующих СМО, имеющих вид:

М смоире = ( R смоире ( ^ ), (М ацп , М ус , М ¹н , М ¹ s ) смоире , п = 1, abs 0, inc 0);

М смовчвфх = ( R смовчвфх ( ^ ), (М ацп , М ус , М 1н , М ¹ s ) смовчвфх , П - 20, abs 0, inc 0);

М смончвфх = ( R смончвфх ( ^ ), (М ацп , М ус , М 1н , М ¹ s ) смовчвфх , П - 5, abs 0, inc 0);

М смотсп/д = ( R смотст ( ^ ), (М ацп , М ус , М 1н , М ¹ s ) смотсп/д , П тст , abs 0, inc 0).

По полученным в СМО результатам экспертная система делает заключения (по имеющимся критериям) о достоверности полученных характеристик там, где в этом есть необходимость, согласно схеме:

Com{[ Nss ( E )] вчвфх , [ Nss ( E) ] нчвфх } 1^ [ Nss ( E )] нчвфх ;

Com{[ Qd ] вчвфх , [ Qd ] нчвфх , [ Qd ", Qd ^н ] тсп } I ^ [ Qd , Qd ", Qd "];

Com{[ Et ] ире , [ Et ] тсп , [ Et ] тсд } I ^ [ Et ];

Com{[ Eti ] ТСП , [ Eti ] тсд } I ^ [ Eti ], где Com – оператор сравнения.

Экспертная система так же производит управление конфигурацией экспериментальной системы, формируя управляющие сигналы по соответствующим разрядам кода на регистре управления. Количество его разрядов ( n _Рг ) указывается в соответствующих моделях блоков управления:

МупрИРЕ = (RУпр('), (s, Мs, Мн, Мувх, Мак, Мацп, Мус, М 1н, М 1 s, Мсмо )упрИРЕ, Прг = 1, abs 0, inc МУВХ);

МупрВФХ = (RУпрВФх('), (s, Мs, Мн, Мувх, Мак, Мацп, Мус, М 1н, М 1s, Мсмо )упрВФХ, Прг = 3, abs 0, inc МУВХ, МАК);

Мупртсп/Д = (Rупртст(*), (s, Ms, Мн, Мувх, Мак, Мацп, Мус, М 1н, М 1 s, Мсмо)упртсп/Д, Прг = 6, abs 0, inc Мs, МУВХ, МАК).

Таким образом полученные оптимальные измерительные структуры по каждому из измерительных каналов будут иметь вид (читаются справа налево):

I	6iaEBA ’ I	NI I EBA I     j 1	I	- 1	I 6N I AOI	I AE I 6AO1 I ^ 1 I
				^ 1			j 1EBA;
I		I NiiAxAO6I		1 , 2 I	- 1^2 I 6N I	AOI I AE I 6AO2 I	^ 2 I j 2AxAOO;
	6iaAxA00
I		I -Л NI i ^ xAOO		1 , 3 I	- 1^з ^6« I	AOI I AE I 6AO3 I	^ 3 I j 3^ xAOO'
	61 Of xAOO
I	61 аоЯ ’ I	NI I ONI I     j 4	I	- 1	I 6N I AOI	I AE I 6AO4 I ^ 4 I
				^ 4			j 40Я ;
I	61 OONA ’ I	NI I ONA I     j 5	I	- 1	I 6N I AOI	I AE I 6AO5 I 1^5 I
				^5			j 5ONA;
I		I NiiONT/A I	- 1	.6 1 -	- Л I 6N I	AOI I AE I 6AO6 I ^	6 I j 6O/I ;
	61 аоя /A ’		s
М   М    М - 1			М - 1		М М	М М М	М
	УпрВФХ	СМОВФХ      s 7		Н7   УС   АЦП   АК   УВХ7   Н7    s 7 Vg

Общая структура системы будет вытекать из совокупности ее оптимизированных измерительных структур и определяться системой измерительных уравнений в операторной форме:

X 1*	= R 2 13	R 2 12	R 2 11	K R 1 14	R 1 13	R 1 12	R 1 11	Y i
^ 2*	= R 2 23	R 2 22	R 2 21	K R 1 24	R 1 23	R 1 22	R 1 21	Y 2
^ 3	= R 2 33	R 2 32	R 2 31	K R 1 34	R 1 33	R 1 32	R 1 31	Y 3
< ^ 4*	= R 2 43	R 2 42	R 2 41	K R 1 44	R 1 43	R 1 42	R 1 41	Y 4
^ 5	= R 2 53	R 2 52	R 2 51	K R 1 54	R 1 53	R 1 52	R 1 51	Y 5
Х б*	= R 2 63	R 2 62	R 2 61	K R 1 64	R 1 63	R 1 62	R 1 61	Y 6
^ 7	= R 2 73	R 2 72	R 2 71	K R 1 74	R 1 73	R 1 72	R 1 71	Y 7

Здесь Y1 - сигнал релаксации емкости гетероструктуры; Y2, y3, у4 - соответственно, высокочастотная емкость гетероструктуры, напряжение Vg(t) и ток I(Vg) через гетероструктуру; Y5, y6, Y7 - соответственно, ток поляризации, ток деполяризации гетероструктуры и температура образца (T, К); R111 – ЭУ ИРЕ; R121 = R131 = R11 – ЭУ ВЧ ВФХ; R141 – ЭУ НЧ ВФХ; R151 = R161 = R171 = R21 – ЭУ ТСП/Д с соответствующими ПИП; R112, R122, R132, R142, R152, R162, R172 – коэффициенты передачи НУ соответствующих каналов; R113, R123, R133, R143, R153, R163, R173 – УВХ для соответствующих каналов; R114, R124, R134, R144, R154, R164, R174 – каналы АК; К-АЦП; R211 = R221 = R231 = R241 = R251 = R261 = R271 = R21 – УС; R212, R222, R232, R242, R252, R262, R272 – масштабирование измеренных величин; R213 – СМОИРЕ; R223, R233, R243 = R23 – СМОВФХ; R253, R263, R273 – СМОТСП/Д, λ1* – измеренное значение Et, λ2*, λ3*, λ4* – измеренные зависимости Cгет(Vg), Vg(t) и Iгет(Vg), соответственно; λ5*, λ6*, λ7*– измеренные зависимости Iп(T), Iд(T) и T(t), соответственно. Следовательно, структурная схема системы будет иметь вид (см. рис.).

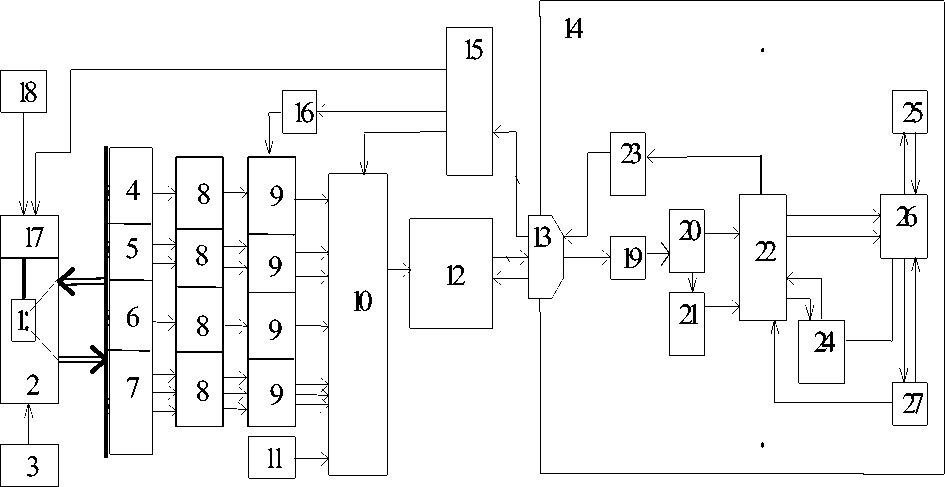
Структурная схема оптимальной адаптивной системы для исследования зарядовых и частотных свойств гетероструктур:

1 – гетероструктура; 2 – программно-управляемый азотный криостат (УАК); 3 – вакуумная система;

4 – ЭУ ИРЕ (М_s3); 5 – ЭУ ВЧ ВФХ (М _{s 1}); 6 – ЭУ НЧ ВФХ (М _{s 2}); 7 – ЭУ ТСП/Д (М _{s 4}, М _{s 5});

8 – блок нормализаторов (М_Н1–М_Н7); 9 – блок УВХ (М_УВХ1–М_УВХ7); 10 – АК (М_АК); 11 – ИОН;

12 – АЦП (М_АЦП); 13 – УС (М_УС); 14 – ЭВМ; 15 – управляющий регистр (РгВыв); 16 – одновибратор;

17 – органы управления УАК; 18 – источник постоянного напряжения;

19 – операция, обратная нормализации (М^–1_Н); 20 , 21 – масштабирование (М^–1 _s ); 22 – все СМО;

23 – блок формирования управляющих воздействий (М_Упр); 24 – ЭС; 25 – блок формирования ЭС;

26 – блок связи с экспертом; 27 – сервисные ПО

В системе также используются программно-управляемый азотный криостат (УАК) [5], обеспечивающий программно-управляемое воздействие на исследуемую гетероструктуру, вакуумная система, обеспечивающая вакуум в измерительной камере не хуже 10 ^–4 Hg, источник опорного напряжения (ИОН) для проверки правильности работы АЦП, одновибратор для формирования строба УВХ, источник постоянного напряжения для питания нагревательного элемента УАК. В программном обеспечении имеются блоки формирования ЭС и связи с экспертом, а также сервисного программного обеспечения (ПО).