Оптимальное управление биопопуляцией с учетом инноваций на модели с возрастной структурой

В данной работе рассматривается задача оптимального управления биологической популяцией по экономическому критерию на основе известной матричной модели [1]. В этой модификации учитываются активные инновационные процессы путем добавления инновационных блоков типа «затраты – выпуск», где «выпуск» трактуется специфически как улучшение параметров исходной модели.

Конкретная цель данной работы состоит в том, чтобы на примере управления стадом крупного рогатого скота (КРС) продемонстрировать все этапы практического исследования, включая концептуализацию модели, идентификацию ее параметров по эмпирическим данным, постановку задачи оптимального управления и ее решение достаточно универсальным методом итерационного улучшения.

В [4] аналогичная задача рассматривалась в общем виде, и упор был сделан на поиск приближенных магистральных решений при идеализирующих допущениях, указывалось на возможность их использования как начальных приближений в универсальных процедурах улучшения. Здесь же, в отличие от [4], реализуется именно процедура улучшения безотносительно к способу задания начального приближения.

1.    Модификация матричной модели биопопуляции и задача управления

Подход, развитый в [2–4] и успешно апробированный в некоторых задачах устойчивого развития регионов, состоит в следующем.

Межгодовая динамика популяции без учета инноваций описывается уравнениями k x1 =^(oitoix1 )* - k1 x1 - u 1, 5c1 = y‘x‘-1 — kixi - u‘, i = 2,...,n,     (1)

i=l где xi – численности возрастных групп, γi – коэффициенты перехода из одной группы в следующую, ki – коэффициенты смертности, σi , βi – параметры рождаемости, ωi – доля женских особей в соответствующей группе, ui – темпы изъятия-пополнения численностей в целях управления.

Пусть Π(t) – экономический эффект на отрезке [t_I ,t] , называемый условно накопленным доходом, динамика которого описывается уравнением вида

П = f (t,x,u,q), t e [t_T,t^] . IF

Через q обозначен вектор параметров, постоянных при отсутствии инновационных изменений, таких как k_i , σ_i , β_i и т. п.

Инновации трактуются как изменение параметров, которое описывается следующими уравнениями:

• 9 = - ([d] + H(t,x,u,q(9)))(9 - 9), k^d = u^d - 5^dk^d, 0 <  d <  Г ^d(k^d) ,   (3)

q¹ = q\ ⁽ 1 + ^Qj^aij ), 1 ^e i j , У,^aij = 1.                   (4)

l e Ij

Здесь d – вектор активных инноваций; [d] – диагональная матрица; k^d , Γ ^d (k^d ) , u^d , δ^d – основные фонды, мощности и инвестиции (векторы) и темпы амортизации в инновационном секторе (диагональные матрицы); θ – вектор инновационных индексов (агрегированное описание изменения параметров исходной модели за счет инноваций); α_lj – весовые коэффициенты; q_I^l – значение в начале наблюдения; H(t, x,u,q) – диагональная матрица, учитывающая различные инновационные процессы, помимо активной инновационной деятельности (например, известную в экономической теории диффузию инноваций); инновации, сопутствующие инвестиционному процессу, и т.п.

Очевидно, активная инновационная деятельность требует дополнительных прямых и фондообразующих затрат, которые принимаются линейными относительно соответствующих управляющих воздействий:

П = f 0 (t,x,u,q) - A^dd - B^du^d ,                      (5)

где A^d , B^d — матрицы-строки коэффициентов прямых и фондообразующих затрат в инновационном секторе.

Задача оптимального управления ставится следующим образом: перевести систему (1), (5) на заданном отрезке времени [t ,t ] из заданного IF начального состояния xI , qI в заданное множество конечных состояний Г при ограничениях на управления u е U(t), 0 < d < dmax и на состояние x е X(t) с максимальным значением H(tF ).

2.    Итерационный алгоритм оптимизации

При практическом решении задачи, по крайней мере на этапе расчетов, предполагается дискретизация дифференциальных соотношений. В связи с этим целесообразно использовать дискретизованную версию модели и применять соответствующий итерационный алгоритм [5].

Задача оптимального управления дискретной системой ставится следующим образом: найти программу u ( t ) и соответствующую ей траекторию x ( t ) (эволюцию состояний), при которой выполняются следующие соотношения

' x ( t + 1) = f ( t , x ( t ), u ), t {t i , t i + 1,..., t p },

< x ( t I ) = x I , x ( t_F ) еГ , x ( t ) е X ( t ), и е U ( t , x ( t )),

, I = F ( x ( t_F )) ^ min (inf).

То есть задана цель управления x ( t_F ) еГ . Необходимо найти программу управления и е U ( t , x ( t )) и соответствующую ей траекторию x ( t ), при которой выполняются ограничения x ( t ) е Х ( t ), а цель управления выполняется наилучшим образом согласно критерию I .

Рассмотрим постановку этой задачи как конкретизацию общей задачи об оптимуме ( M , D , I : M ^ R ). За множество M примем совокупность всевозможных пар функций m = ( x ( t ), и ( t )). Множество D выделяется из M следующими связями и ограничениями:

x(t +1) = f (t, x(t), и), и е U(t, x), x е Х(t), tI, tF,x(tI) = xI фиксированы, x(tF) еГ. Требуется найти минимизирующую последовательность {ms} с D , на которой I(ms) ^ I* = inf I.

Будем применять принцип расширения и достаточные условия оптимальности. Введем в рассмотрение следующие конструкции:

R ( t , x , u ) = ф( t + 1, f ( t , x , u )) - ф( t , x), ц( t ) = sup     R ( t , x , u )

u e U ( t , x ), x e X ( t )

G (x) = F (x) + ф( tF, x) - ф( t,, x ,), l = inf G (x), x eFn X (tF).

tF ^- 1

Составим с их помощью функционал L = G ( x(t_F )) - ^ R(t , x(t ), u(t )) t_I

(обобщенный лагранжиан). Легко проверить, что L = I на D, отсюда следует, что если имеется элемент т1 e D и элемент т11 такой, что

L(т1 )>L(т11), и если т11 eD, то I(т1 )>I(т11). Задача улучшения управления для L проще, потому что она рассматривается без рекуррентной связи (дискретной цепочки).

Далее речь пойдет о задаче:

x ( t + 1 ) = f ( t , x ( t ) , u ) , u e U , 1 = F ( x ( t F ) ) ,

T = { t₁ ,..., t_F } - задано, x ( t₁ ) = x₁ - задано. Если задача дана с другими ограничениями, то избавиться от дополнительных ограничений можно известным методом штрафов.

Чтобы задачу улучшения решать наиболее эффективно, целесообразно сводить ее к задаче оптимизации в достаточно малой окрестности известного элемента m^I на упрощенной модели. Чтобы улучшенная траектория не вышла из заданной окрестности, надо локализовать задачу, т.е. добавить дополнительное условие | u - u'(t) <  а . Рассмотрим разность

A R = R ( t , x , u ) - R ( t , x¹ ( t ) , u¹ ) .

Линеаризуем ее и заменим моделью:

AR = AR^y + AR„U, xu где y = x-x1 (t), и = u -u1 (t), y0 = x0(t), (ARx,ARx0,ARJ) - вектор частных производных, которые берутся на элементе m . Дальше будем максимизировать эту конструкцию по y , υ.

Введем в рассмотрение функцию

H ( t ,^, x , u ) = ^f ( t , x , u ) .

Тогда A R запишется так:

AR = H (^ (t +1), x1 (t), u1 (t)) xy + HU - ^ (t) y.

Будем максимизировать A R . Полагая, что A R ® R x A x + A _uR , будем выбирать и = A u   так, чтобы и было достаточно малым

(| U <  а ), ( u¹ ( t ) + и ( t )) е U ( U считается для простоты постоянным множеством). Иначе говоря, υ будем подбирать так, чтобы

( u I ( t ) + и( t )) е U_a = { и е UI |U <  а }.

При достаточно малом α отклонение от соответствующего приращения A x будет малым. Модификация состоит в том, что вместо аналитического представления для υ получается значение υ , которое находится в множестве U_α . В процессе вычислений дело сводится к численному перебору на этом множестве α . Это дает возможность учесть ограничения на u непосредственно без использования штрафных функций.

tF ^- 1

Функционал AL тогда будет представлен так AL=~^AuR, и если при-tI ращение AuR > 0 , то AL < 0 .

• 1.    Просчитывается цепочка

• 2.    Находится υ_α непосредственным поиском в окрестности u .

• 3.    Делается прямой счет

• 4.    Для различных α вычисляется F(x_α (t_F )) , и это минимизируется по α , т.е.

• 5.    Вычисляется и¹¹ (t) = u¹ (t) + u_a .

• 6.    Управление u ^II ( t ) принимается за новое u ^I ( t ) , и начинается новая итерация.

^(t) = - H_x(t,^(t + 1 ),X (t),U (t))

при начальном условии на правом конце

V ^(tF ) = - ^Fx ^{(X (t}F )) .

x(t + 1 ) = f(t,x(t),u I (t) + u_a(t)) .

^F(Xa⁽ t F ) ^ min ^ a * .

α _α

Критерий остановки – функционал перестает улучшаться.

3.    Модифицированная модель стада КРС и ее информационное обеспечение

Рассмотрим приложение модифицированной модели биопопуляции из раздела 1 к задаче эксплуатации стада КРС с численностями животных 19

x ¹ , x ² , x ³ в трех возрастных группах: от 0 до 1-го года, от 1-го до 2-х лет и от 2-х лет и старше. По содержанию и уходу наиболее затратны 1-я и 2я группы. Из 1-й и 2-й групп возможна продажа живого скота, 2-я и 3-я группы используются для производства мяса и мясопродуктов, а 3-я группа – еще и для производства молочной продукции. Предполагается, что инновации приводят к уменьшению коэффициентов прямых затрат по содержанию и уходу a_i и увеличению годовых надоев от одной коровы μ . Динамика накопленного дохода описывается уравнением:

^П = £ (P i u ) + P 4 Ц ^x 3 - £ ^(a i x‘) - A d d ,             (6)

i = 1                                      i = 1

где ρ_i – цены на соответствующие виды продукции, a_i – удельные расходы по содержанию скота. В терминах общей модели получится 4-мерный вектор параметров q = (a₁ ,a 2 ,a ₃ ,ц - ц) ( ц -максимально возможное значение ц ). Агрегирование не производится, т.е. О = q .

Требуется определить политику ведения хозяйства на заданном промежутке времени [t ,t ] , т.е. функции u(t) , d(t) , обеспечивающие мак-IF симальное значение H(tF) (минимум функционала I = -H(tF)) при следующих граничных условиях и ограничениях:

0 ^ u ^ u max ,⁰ ^ d ^ d max , x ^(tI ) = xl , x ^(tF ) = x F , ⁿ (tl) = ⁰ , q ^(tI ) = q i , X i - x \ .

Последние означают, что поголовье в каждой возрастной группе не должно уменьшаться ниже границы, определяемой из биологических и эксплуатационных соображений.

Описанная модель является концептуальной. Информационное обеспечение состоит в том, чтобы разработать и реализовать методики формирования таблиц параметров концептуальной модели, исходя из их содержательного смысла, с использованием первичной статистической информации, разнообразных литературных и документальных источников, целенаправленных эмпирических исследований и экспертных оценок.

Проблемы информационного обеспечения, с учетом сложностей получения междисциплинарных данных о взаимодействиях различных компонентов единой системы, представляются наиболее сложными. Они рассмотрены подробно в [6] вместе со способами их решения. Среди них отметим методологию абстрактных (виртуальных) экспериментов, которая существенно использует математические преобразования модели для выявления содержательного смысла многочисленных неизвестных параметров модели и формулирования соответствующих запросов на языке предметных специалистов. С помощью этой методологии был сформирован содержательный запрос на эмпирические данные (табл. 1):

Таблица 1

Параметр	Содержательная характеристика
γ 2,3	коэффициенты перехода из одной группы в следующую: расчет, исходя из естественного взросления
k i	коэффициенты смертности: каков процент скота вымирает в год в i-й группе
σ , β	параметры плодовитости: каков приплод от одной коровы в год
ω	доля коров в стаде
μ	годовые надои от одной коровы
µ	максимально возможное значение μ
A d	матрицы прямых затрат на инновации: примеры, сколько стоит повышение надоев и плодовитости путем приобретения более породистой коровы, улучшения условий содержания в пересчете на 1 единицу
ρ i	цены на соответствующие виды продукции (мясо, молоко, живой скот)
a i	удельные расходы по содержанию скота: расходы на 1 единицу в год в соответствующей возрастной категории

В результате обработки этих данных, дополненных условными на основе экспертных оценок, получены следующие значения параметров модели (табл. 2)

Таблица 2

Параметр	Способ расчета	Значение
γ 2	1 , где m – число возрастных групп m	1
γ 3	1 , где m – число возрастных групп m	1 3
k	определяется непосредственно из эмпирических данных о падеже скота	[0.1, 0.01, 0]
σ	dx 1           1 σ =      , где dx имеет смысл при- ωx 3 роста в год в 1-й группе	1
β	определяется непосредственно из эмпирических данных о выходе телят	0.8
ω	определяется непосредственно из эмпирических данных о поголовье скота	0.73
μ	определяется непосредственно из эмпирических данных об удоях	1 900

µ	определяется непосредственно из эмпирических данных об удоях	2 100
Ad	экспертная оценка с использованием эмпирических данных	[6 000, 9 000,0,0]
ρ	информация из интернета	[80, 150, 150, 15]
a	экспертная оценка с использованием эмпирических данных	[9 000, 6 500, 7 000]

4.    Программное обеспечение и вычислительные эксперименты

Итерационный алгоритм из раздела 2 был реализован применительно к задаче управления поголовьем КРС в системе MAPLE-13, и проведена серия вычислительных экспериментов. Основные результаты представлены на рисунках 1-8 и в таблице 3.

В таблице показано изменение функционала по итерациям.

Таблица 3

№ итерации	Уровень накопленного дохода
0	1 350 241
1	2 458 295
2	2 458 295

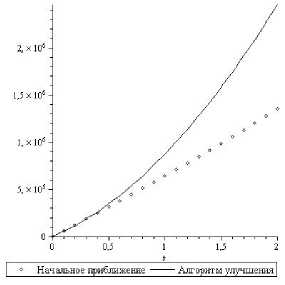
Рис.1. Уровень накопленного дохода

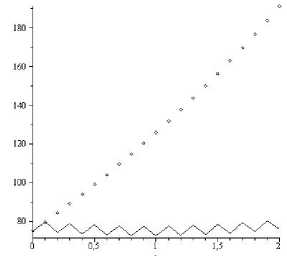
| * Начальное приближение-----Алгоритм улучшения |

Рис.2. Поголовье скота в 1-й группе

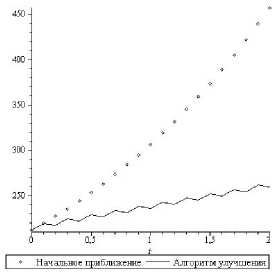
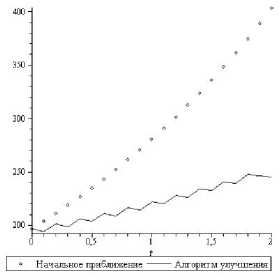
Рис. 3. Поголовье скота во 2-й группе Рис. 4. Поголовье скота в 3-й группе

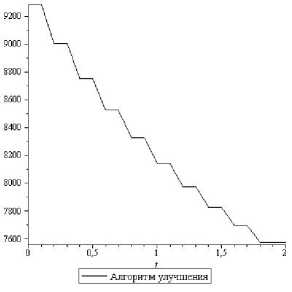
Рис.5. Удельные расходы в 1-й группе ( q ₁ )

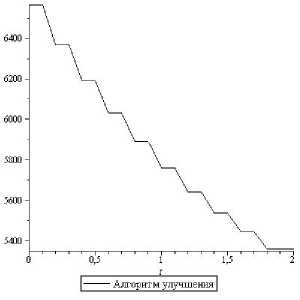
Рис.6. Удельные расходы во 2-й группе ( q ₂ )

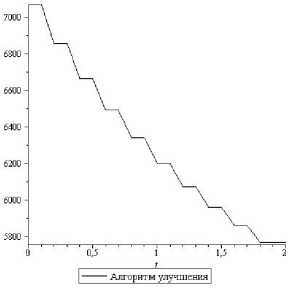
Рис.7. Удельные расходы в 3-й группе ( q ₃ )

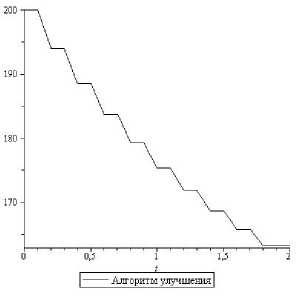
Рис. 8. Удои ( μ - μ )

Зигзагообразный характер улучшенной траектории объясняется спецификой для применяемого алгоритма формирования управления в виде скользящего режима, который может быть заменен эквивалентным ос-редненным. Это соответствует гладкому осреднению полученной траектории, что не представляет затруднений.

Представленные результаты вычислительных экспериментов демонстрируют высокую эффективность применяемого универсального алгоритма улучшения для рассматриваемого класса задач с системой связей, близкой к линейной: практическая сходимость обеспечивается за одну итерацию (при том, что итерация содержит серию прогонов задачи Коши для исходной системы).

Заключение

Таким образом, построена модификация достаточно общей матричной модели биопопуляции с учетом инновационных процессов, и сформулирована задача оптимального управления по экономическому критерию эффективности. В качестве приложения исследована задача управления поголовьем КРС. Проведены эмпирические исследования по информационному обеспечению на примере крупной фермы, исходя из требований концептуальной модели с привлечением разнообразных источников и экспертных оценок. Для решения конкретной задачи оптимального управления применен универсальный итерационный алгоритм, основанный на достаточных условиях оптимальности и улучшения.

С этой точки зрения, данную работу можно рассматривать и как продолжение [4], где получено эффективное начальное приближение (магистральное решение), но не представлен алгоритм его улучшения. А также ее можно применять и как самостоятельную (из области моделирования популяций с возрастной структурой) для исследования различных проблем, включая демографические, когда специфическое магистральное решение получить не удается, и используются весьма произвольные начальные приближения. Полученные результаты показывают высокую эффективность применяемого алгоритма оптимизации в подобных условиях.