Оптимальное восстановление гармонической функции по неточно заданным значениям оператора радиального интегрирования

В общем случае задача оптимального восстановления состоит в наилучшем приближении значения линейного оператора на некотором множестве по информации, являющейся значениями другого линейного оператора (называемого информационным), заданными с погрешностью в той или иной метрике (см. [1–3]). Во множестве случаев задачи оптимального восстановления операторов сводятся к задачам линейного программирования, впервые появившимся и получившим мощное развитие в работах Л. В. Канторовича, в которых были разработаны эффективные методы решения и анализа таких задач. В случае с задачами оптимального восстановления, соответствующие им задачи линейного программирования удается решить явно из-за небольшого числа присутствующих в них ограничений. В конкретных задачах восстановления в качестве информационного оператора обычно рассматривают линейные функционалы или операторы, сопоставляющие функции ее значения в точках, ее коэффициенты Фурье или просто саму функцию. Подобные задачи рассматривались во многих работах, начиная с [4]. Упомянем лишь некоторые из недавно опубликованных работ на эту тему — [5–8]. В настоящей работе рассматривается оператор, ставящий в соответствие функции множество ее интегралов, взятых вдоль радиусов единичного шара в R ^d . Такого рода операторы применяются для моделирования различных томографических процессов и подробно изучаются в теории компьютерной томографии [9]. В теории оптимального восстановления информационные операторы томографического типа рассматривались ранее в [2, пример 3.2].

Рассмотрим пространство h^ гармонических в шаре Bd = {x G Rd : |x| < 1}, d > 2, функций, для которых конечна норма kf kh2 = sup kf (r^)kL2(sd-1), 06r<1

S ^d-1 = { x g R d : | x | = 1 } .

Следуя [10], будем называть h 2 пространством Харди гармонических функций. Известно представление функций из h 2 в виде разложения в ряд по ортонормированной системе сферических гармоник:

га N ( l,d)               , х

f (x) = E Ef^i ¹ Y ll A , l=0 k=1             ^^{| x|/}

где

N(l’d) = (2±^7-R+1-5}1' 1 > !' N(°'d) = L l!(d — 2)!

Рассмотрим оператор радиального интегрирования K , определенный равенством

Kf (Z ) = fr(rZ ) dr, Z G S ^{d - 1} .                            (2)

Предположим, что для любой функции f G Bh 2 = {f G h 2 : k f k h ₂ 6 1 } значение Kf известно с некоторой погрешностью, т. е. дана функция g G L 2 ( S ^{d - 1} ) такая, что WKf — g k L ₂ (S d-¹ ) 6 5. Зная функцию g , мы хотим наилучшим образом восстановить функцию f . Воспользуемся тем, что h 2 непрерывно вложено в L 2 ( B ^d ) и будем искать приближение в этом пространстве. Рассмотрим всевозможные методы восстановления — произвольные отображения m: L 2 ( S ^{d — 1} ) ^ L 2 ( B ^d ) . Для каждого m определим величину, называемую погрешностью метода

e^(Bh 2 '^K'5^,m)=       SUp        WmS) ^{— f} k L ₂ (B d ) .

f EBh 2 , k^{Kf — g k}L₂(S^d-1) 6^

Оптимальным назовем метод, который имеет наименьшую погрешность, т. е. тот, на котором достигается погрешность оптимального восстановления

E(Bh 2 ,K,d)=       inf       e(Bh 2 'K'6,m).                 (3)

m: L.^' d        ■/.,(B^d)

Теорема 1. Положим

^(х 0 'У 0 ) = ⁽⁰' О),

. i ² ' 2i + d — 2 )' i = 1' ² •••'

y s+1 — y s    -?     y s X s +1 — y s +1 X s

1 = ----------' ^2 = ---------------- xs+1 — xs            xs+1 — xs где число s > 0 таково, что xs <5 2 6 xs+1. Тогда погрешность оптимального восста- новления равна

/----            ----

E(Bh 2 'K'5) = VA 1 + А 2 5 ² .

Методы

^ N ( l,d )

m a (g)(x) =ЕЕ a kl ^{(l + 1)g} kl | x | l Y kl l=0 k=1

x

| x | ^,

где gkl — коэффициенты разложения функции g в ряд Фурье по ортонормированной системе Ykl gki = У g(Z)Yl(Z) dZ'

Sd-1

b2         .      у A1A2(l + 1) /-у                 2l + d~ akl =   ----~ ~+ ekl^~----~---~\ A1(2l + d) + A2 ,    x2 - 1,(7)

A i (l + 1)² + A 2       A i (l + 1)² + A2V                  ^{(l + 1)2}

€ ki — произвольные числа из отрезка [ — 1; 1], которые являются оптимальными.

<1 С экстремальной задачей (3) тесно связана двойственная к ней задача kfkL2(Bd) ^ maX- f £ Bh2- kKf kL2(Sd-i) 6 5(8)

Эта связь подробно изучена и описана в [3] и других работах тех же авторов. Нам же потребуется следующее утверждение:

E⁽Bh 2 ^,K,5') >       sup       k f k L 2 (B d ) .

f EBh ^ , k^{Kf k} L₂(S^d-1) 6^

Действительно, если функция f допустима в (8), то функция - f также является допустимой. Поэтому верна цепочка неравенств

^SUP       HS) ^{- f} k L 2 (B d ) >      ^SUP      llm ^{(0) - f} k L 2 (B d )

f EBh2,                                    f EBh2, kKf—gkL2(Sd-1) 6^                             kKf kL2(Sd-1) 6^

ll^{m (0) - f} k L ₂ (B ^d ) ⁺ k ^{- m(0) - f W} L ₂ (B ^d )

> SUP ---------------------4--------------------- >      SUP      Wf WL2 (Bd )• f EBh2,                             2                                f EBh2, kKf kL2(Sd-1) 6^                                                             kKf kL2(Sd-1) 6^

Таким образом, погрешность оптимального восстановления ограничена снизу значением двойственной задачи. Решив ее, получим явное выражение для этой оценки.

Из (1) следует

^ N (l,d)„

Kf(Z) = E E Tf+rYkl(Z)• l=0 k=1 1

Используя (1), (2), (9) и равенство Парсеваля, получим следующие формулы:

^ N(l,d)

WfWL2(Bd) = E E ^- l=0 k=1

^ N (l,d)

WfWh2 = E E fk^2- l=0 k=1

^ N (l,d)        _|2

WKf « 1 , . ) = EEfU l=0 k=1    ⁺ '

Введем обозначение

N ( l,d )

bl = E ifkii2- k=1

Тогда задача (8) может быть переписана в виде

∞   ∞∞

XXX 2T++d ^ ^max- XXX b l ⁶ *• XXX (i+ l i) 2 ^{6 52}- b l > ^{0             (10)}

(для удобства мы рассматриваем квадраты функционала и ограничений). Функция Лагранжа этой задачи имеет вид

L(b,Ai , A2) = —Ai - A252 + XX l=0

b l

(l +1) 2

A i (l + 1) ² + A ₂ —

(l + 1) ²

2l + d ,

b — (b o ,b i ,...).

Множество точек { (x i , y i ) : i >  0 } , определенное в (4), лежит на графике функции y = ₂ ^ x + d - 2 , которая является вогнутой при x >  0 . Отсюда следует, что все это множество лежит под прямой, соединяющей соседние точки (x i ,y i ) и (x i+1 ,y i+1 ) (см. рис. 1). Прямая, соединяющая точки (x s , y s ) и (x s+1 ,y s +1 ) , имеет вид y = A 1 x + A 2 , где A 1 , A 2 определены в (5). Тогда y i 6 A 1 x i + A ₂ , i >  0. Подставляя i — l + 1 , получим

(2+12 6 Ai (i + 1)2 + A• откуда следует, что L(b, A1, A2) > — A1 — A252.

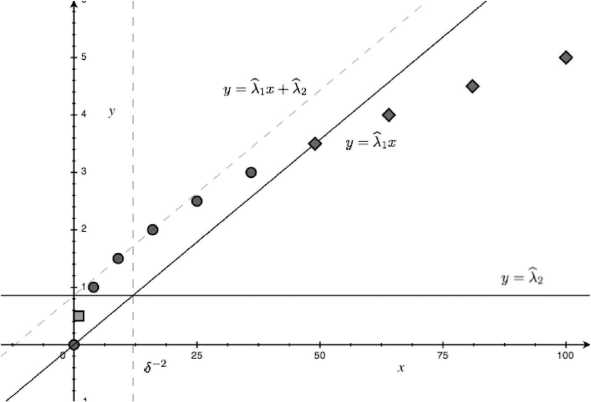
Рис. 1. На рисунке изображено множество точек {(x l , y l ) 1 1 >  0}, при 5 -2 = 12, d = 2.

Точки, изображенные квадратом, соответствуют тем значениям l, для которых можно положить a kl-1 = 1, k = 1,..., N (1, d), ромбом — тем 1, для которых a _kl-1 = 0, k = 1,..., N (1, d).

Пусть x s <5 ² 6 x s+1 . Тогда определены неотрицательные числа

А _ 52 xs+i — 1 a _     1 — 52 xs bs — xs            , bs + 1 — xs + 1

x s+i ^— x s                 x s+i ^— x s

Положим b i — 0 , при i / { s, s + 1 } . Тогда получившийся набор b допустимый в (10), удовлетворяет условиям дополняющей нежесткости

/^

b i

∞

Eb i l=0

∞

+ b2 ( Т l=0

b l

(l+1) ²

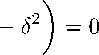
и доставляет минимум функции Лагранжа

/—   /—          /^ ^^   /^          ^^     ^^

min L(b, A 1 , Х 2 ) — L(b, Х 1 , A 2 ) — — А 1 — b ₂ 5 . b l >0

---ч ---ч

В силу того, что Ai,A2 > 0, верно неравенство откуда

---ч ---ч

L(b,A i ,А 2 >

∞

- X

1=0

b l

21 + d’

---ч ---ч min L(b, Ai, А2) 6 bi>0

min b i > 0 , P^ o b l 61, P ^  bl <Л2 2^l=0 (i₊i)2 6°

∞

- X l=0

b l

21 + d"

Но из (11), (12) следует

---4     ---4                    ---4  ---4     ---4 min L(b, A i , A 2 ) = L(b, A i , A 2 ) b i > 0

∞

- ^X

---4

b l

21 + d"

Таким образом,

∞

-

---4

b l

21 + d

6 min bi>0,

PSo b i 6 1 , P^o^ 6° ²

∞

-X l=0

b l

21 + d’

---ч означает, что набор b является точкой максимума

в

задаче (10). Решение этой задачи

равно A i + A 2 ^ ² , а решение задачи (8), соответственно,

/.--4            ---4

— у ^Xi + ^X 2 § ² .

Итак, мы оценили погрешность оптимального восстановления снизу E(Bh 2 , K, 5) >  у/b i + ^X 2 ^ ² . Покажем теперь, что на самом деле в этой оценке выполнено равенство.

Рассмотрим метод m a , определенный в (6). При A 2 = 0 (эквивалентно s = 0 или 5 >  1 ) из (7) следует, что a = (0) и m e (g) = 0 . Тогда

sup f евн ₂ , k^Kf—gk L₂(S^d-1) ⁶ °

11^т0 ⁽д) ^{- f} llL ₂ (B d ) ⁶ sup IlfllL ₂ (B d ) ^{6 A} i - f eBh ₂

При A 2 > 0 , используя (1), имеем

i fll2 X V^ (ak1(1 + 1)gk1 - fk1)2 HMg) - f kL2(Bd) = 2^ 1. ------2Г+1------ l=0 k=i

^ N ( 1,d )

= XX l=0 k=i

a _kl (1 + 1)(g _kl

^— 1+1 ) ^{+ f} k1 ⁽a k1 ^— 1))

21 + d

Применяя неравенство Коши — Буняковского |h x,y i| 6 | x |k y k к векторам

x=

a k1 ^{(1 +} 1) q^

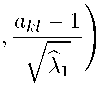
y=

A^b 2

^g kl

-

f kl

!"+у ) ’ V ^A i ^f k1 ) ’

получим

II ( f II2      < \" \" 1 (ak1(1 + 1)2 (ak1 - 1)2 \f\(        fk1 \2 f2 A lima(g) - f kL2(Bd) 6 X X             X----- +  T---- / ( A2 Vkl -     ) + Aifk1 / "

_{l =0 k =i} 21 + d A ₂             A _i                   1 + 1

Введем обозначение д _    1 (aki (1 + 1)2 , (aki - I)2 A

^kl = 21 + dV b 2     ⁺ b i У

Тогда

e(Bh 2 ,K,5,m a ^{) 2} =       sup       ||m⁽g^{) —} f k L (B d )

f GBh 2 ,                         2'

k^Kf - ^gk L₂(S^d-l) ⁶^

6 sup f GBh2, kKf—gkL2(Sd-1)6

^ N ( i,d)      ,

E E A« ^2 (g ki - i=0 k=1

fr) ² +f.

Равенства (7) эквивалентны неравенствам A ki 6 1 , откуда

~ N ( l,d )              _f 2 b        b b

e(Bh2,K, 5, ma)2 6      sup ^^ ^^ ( b2 gkkl —     ) + b1f2i ) 6 b252 + bl- f GBh2,                 V V 1 + 1/          У kKf-g\k2(sd-i)68l 0 k 1

Таким образом, мы получили, что оценки снизу и сверху для величины E(Bh2, K, 5) совпадают. Отсюда немедленно следует утверждение теоремы ma

) 6 ^/^b 1 + ^b 2 5 ² . >

Vbl + b252 = sup     kf kL2в) 6 E(Bh2, K, 5) 6 e(Bh2, K, 5, f GBh2, kKf—gkL2(Sd-1) 6^

Определенный в теореме 1 набор коэффициентов (a ^i ) является фильтром, определяющим значение каждой гармоники в восстановлении функции f . Заметим, что при 5 >  1 погрешность оптимального восстановления становится равной ^^, а оптимальным оказывается метод m o (g) = 0 . Покажем, что в зависимости от величины погрешности 5 некоторые гармоники не нуждаются в фильтрации, а другие вовсе можно не учитывать.

Следствие 1. Пусть выполнены условия теоремы 1. Тогда можно положить a ki = 0

1 / Т           1       (i+1)2 / Т пРи 2l+d 6 А1 и aki = 1 пРи 6 Х2.

C Подставляя a ki = 0 и a ki = 1 в (13), получаем, что условие A ki 6 1 эквивалентно, (i+1) ²

соответственно, условиям 2i+d 6 ^Ь 1 и 2Z +d" 6 ^А 2 . в

Приведенное следствие означает, что, начиная с некоторой степени, все гармоники большего порядка не влияют на погрешность восстановления и коэффициент перед ними можно взять равным нулю. Также все гармоники, степень которых не превосходит определенного значения, не нуждаются в фильтрации и коэффициент может быть выбран равным единице. С ростом погрешности измерения δ число ненулевых коэффициентов в наборе a уменьшается, пока они все не становятся равными нулю при 5 >  1 . При уменьшении погрешности измерения δ увеличивается число гармоник, не нуждающихся в фильтрации, а оптимальный метод m _a переходит в точную формулу восстановления

^ N ( i,d )

x

| x | ^.

m i ⁽g) = X X ^{(1 + 1)}g ki ^{1 x11} Y ⁱ i =0 k =1

Сказанное проиллюстрировано на рис. 1. На рис. 2 указаны области значений фильтра a , при которых метод m a (g) является оптимальным. Видно, для каких 1 значение a ki , к = 1,..., N(1, d) , может быть взято равным 1 или 0.

Решая задачу оптимального восстановления функции f по неточно заданному значению оператора K , мы считали, что информация, которой мы владеем есть функция g G L 2 ( S d^-1 ) , удовлетворяющая условию || Kf — g | L ₂ (s d-i ) 6 £• В действительности, мы сразу перешли от функций f и g к рассмотрению их рядов Фурье и далее работали лишь с наборами коэффициентов Фурье { f _kl } и { g _kl } . Предположим теперь, что вместо всего множества { g kl } нам известно лишь конечное число первых его элементов. Получим следующую задачу. Пусть для каждой функции f G Bh 2 нам известен набор g G R q , q = P N0¹ N(l, d) такой, что

N - 1 N ( l,d )

E E iKf ki — g ki i ² 6 ^ ² , l=0 k=1

где

Kf ki = J Kf (Z)Y l (Z ) dZ.

S d^-1

В качестве методов восстановления рассмотрим отображения m : R q ^ L 2 ( B ^d ) . Определим погрешность метода

^e(Bh 2 ^,K,5^,m)=           sup            k^m(g) ^{— f} k L ₂ (B d )

f EBh 2 ,

P N^-1 P™ IKf ik -g ik V ² 6 S 2

и погрешность оптимального восстановления

E (Bh ₂ ,K,6) =    inf     e(Bh ₂ ,K,5,m).

m : R q ^ L ₂ (B ^d )

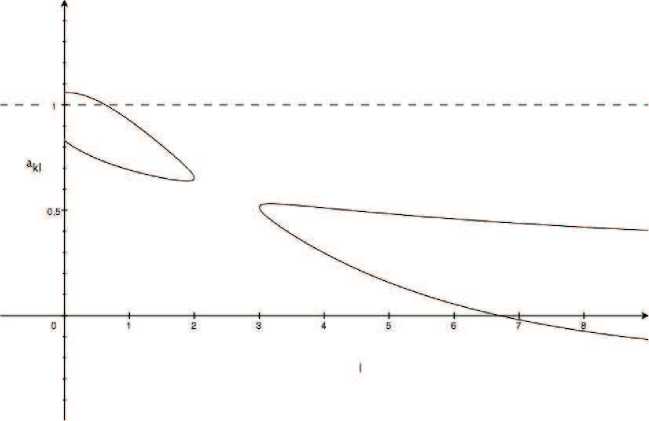
Рис. 2. На рисунке изображена область возможных значений фильтра a kl , k = 1,.. ., N (l, d), в зависимости от параметра l, при 5 ^-2 = 12, d =2.

Теорема 2. Положим

⁽x i ,y i ) =

i ²

i ²

, 2i + d — 2

^y N +1    ys+1    ^y s 1

i = 0,1,..., s n = min s >  0 : ------ > ----------- >,

X N +1    X s+1 — X s

E    y s+1

A1 = ---- xs+1

-

-

y s x s ^,

y s x s +1

^A 2 = ------

-

y s +1 X s

x s+1

-

x s

при x _s < δ

² < X s+1 , 0 6 s < S N ,     (14)

---ч λ

y N +1    v

= -----’ ^A 2 = ys_N

X N +1

-

---ч

X s N A 1 при 5

> ^X S N •

Тогда погрешность оптимального восстановления равна

/ ---4          ---4

E(Bh 2 ’K^ = VA 1 + A 2 ^ ² .

Методы

N-1 N (l,d)                         , x ma(g)(x) = 52 52 akl(l + 1)gkl |x|l Y^W )’ l=0 k=1                      Xlxl/

где a _kl , определенные равенствами (7) , являются оптимальными.

<1 Рассмотрим двойственную задачу

N - 1 N ( l,d )

kf k L ₂ (B d ) ^ ^max, ^{f e B}h 2 , X X \^Kf lk | ^{2 6} ^ l=0 k=1

Аналогично доказательству теоремы 1, получим оценку снизу

E(Bh 2 ,K,5) >

sup f €Bh 2 , p N ^-1 p N^-d) iKf ik i ² 6 s ²

kf ^k L ₂ (B d ) •

Переходя к квадратам функционала и ограничений, используя (9) и обозначение b i = P ^N=i^d) I f kl l ² , перепишем задачу (17) в виде

∞b

Е —^ max,     b 6 1,

2l + d ’ l=0

N -1   A

E 6     b i >  a

Функция Лагранжа этой задачи имеет вид

∞

^L(b, ^A1, ^A2 ) = ^{— A}1 ^{— A}2⁵2 ⁺ X /7,-142 l=0 ^{(l + 1) 2}

^A 1 ^{(l + 1) 2 + X} N ^(l)A 2 ^— 21^+ d

,

где X N (l ) — характеристическая функция множества { 0, • • • ,N — 1 } , b = (b o , b 1 , • • •) .

Рассмотрим два случая.

Пусть xs < 5-2 < xs+1, s < sN. Выберем A1 и A2 как в (14). Следуя тем же рассуждениям, что и в доказательстве теоремы 1, получим yj+1 6 A1Xj+1 + A2, j 6 N — 1-При j > N, имеем b             _ ys+1 — ys            x yN+1            x n

^A 1 x j+1 ^y j+1 =     _ ^X j+1 ^y j+1 >       ^X j+1 ^y j+1 >  ⁰

x s+1 x s                ^X N +1

Таким образом, выполнено неравенство L(b, A1, A2) > — A1 — A2^2^ Положим bs = Xs 52Xs+1   1, bs+1 = Xs+1 1 52xs xs+1 - xs               xs+1 - xs bi = 0 при i / {s, s + 1}. Тогда получившийся набор условиям дополняющей нежесткости

---ч b допустим в (18), удовлетворяет

( ^      \       / N — 1

XA - 1 + Ц X 1=0       /       X 1=0

и доставляет минимум функции Лагранжа

---ч b l

(l+ 1) ²

-

=0

min L(b,A i ,A 2 ) = L(b,A i ,A 2 ) = L(b,A 1 ,A 2 ) = b i >0

---4

— A1

- А 2 Й ² .

Отсюда (аналогично доказательству теоремы 1) следует, в задаче (18), что означает что

---ч b доставляет максимум

E (Bh 2 ,K,S) >  b l + ^A 2 S ² .

Пусть S 2 > Xsn . Выберем Ai и A2 как в (15), так что прямая y = Aix + A2 проходит через точку (xsN ,ysN) параллельно прямой у = У^^^ х. Тогда при 0 6 j 6 s— — 1 имеем yj+1 6

y s ^- y s - 1                    y s ^- y s - 1

-----------X j + 1 + y s N — X s n----------- x s N ^- x s N - 1                 x s N ^- x s N - 1

(точки (xj+i,yj+i) лежат под прямой, соединяющей (xsn—i,ysN-1) и (xsn,ysN)), откуда yj+1 6 ysN — ^"N ^"N (xsjv — xj+1) 6 ysN — ^ + (xsjv — xj+1) = A1xj+1 + A2-Xsn — X"n — 1                     X-+1

При s— 6 j 6 N — 1 выполнено ys +1 — ys                   ys +1 — ys yj+1 6 -----------Xj+1 + ysN — XsN-----------

X s n +1 — X s n                x s N +1 — X s n

(точки (xj+1,yj+1) лежат под прямой, соединяющей (xsn,ysN) и (xsn+1,ysN+1)), откуда yj+1 6 ysN + ^ N +---^"N" (xj+1 — xsN ) 6 ysN + ^ + (xj+1 — xsN ) = A1xj+1 +

XsN + 1 — XsN

Если j > N, то

A             (     11 A .

^{A 1} x j y j = x j <2N + d — 2   2j + d — 2 J > ⁰

Таким образом, выполнено ---- ----         ---- --- ^

L(b, ^A 1 , ^A 2 ) > — ^A 1 — ^A 2 ^ .

Положим b i = 0 , i / { s _N — 1, N } , b _s N _{— 1} = S ² x _s N , b _N = 1 — 6²x _s N . Тогда набор ^A допустим в (18), удовлетворяет условиям дополняющей нежесткости

/ ^      \      N-—1   a\

A1 ( XA1 — 1) + A2 ( X (7+l1p — 5) = 0 1=0

и доставляет минимум функции Лагранжа

---- ----          ---- ---- ---- ---- ---- ^ min L(b, A 1 , A 2 ) = L(b, A 1 , A 2 ) = — A 1 — A 2 S . b l> 0

Отсюда E(Bh ₂ ,K, S) > ^/A ₁ + ^A 2 S ² .

Для произвольного 6 рассмотрим метод ma, определенный в (16). При A2 = 0 из (7) следует, что a = (0) и mg(g) = 0. Тогда sup           km(g) - fkL (Bd) 6 sup kf kL (Bd) 6 A1.

f eBh ₂ ,                                  ' ' f eBh₂         ' '

P N^-1 P™ IKf ik -g ik l ² 6 6 2

При A2 > 0 имеем

N - 1 N ( l,d ) kWg) ^{- f} ku (B d ) = X X l=0 k=1

^(a kl ^{(l + 1)g} kl - ^f kl ^{) 2}

2l + d

^ N ( l,d )

XX l = N - 1 k=1

(a kl ^{(l + 1)(g} kl - f l ) ^{+ f} kl ^(a kl - 1))

2l + d

^ N ( l,d )

+ XX l=N k=1

^ N ( l,d )

+ XX l=N k=1

2 ^f kl

2l + d

^f kl

2l + d"

Аналогично теореме 1 применим неравенство Коши — Буняковского, получим

N-1 N (l,d)      , p 9           \ m N(l,d)   ^2

Tfkr) +  - XX ^

++

⁷ l= N k =1

km a ^{(g) - f} llL ₂ (B d ) ⁶ XX A kl (b2 g 9k l ^- l=0 k=1

где A ki определено в (13). Равенства (7) эквивалентны неравенствам A ki 6 1 . Заметим также, что 2N _d 6 ^A 1 и потому с^ 6 ^А 1 при l >  N . Тогда

^e(Bh 2 ^,K,5^,m a ^{) 2} =           ^suP            ^{к т(}д) ^{- f k} L ₂ ( _B d )

P N=^-1 P N f IKf _lk -g _lk l ² 6 8 2

N - 1 N ( l,d )

6           sup                   ^A A 2 g kl -

« , _N<^faB^fl2’             l=0 k=1

P N^-1 P N=1'^d) IKf _lk -g _lk l ² 6 6 ²

_{f 2}    ^ N ( l,d )

1+1) ⁺ X X ^A 1 ^{f 2}l ^{6 A} 2 ⁶ 2 ^{+ A} 1 " >  l=0 k=1

В рассмотренном выше случае мы располагали неточной информацией о конечном наборе первых коэффициентов Фурье функции Kf , причем отличие этой информации от точной мы измеряли в метрике I 2 . Пусть теперь нам дан набор чисел {6 kl >  0 : l = 0,..., N — 1, k = 1,..., N(l, d) } , характеризующий неточность информации для каждого коэффициента g kl в отдельности, т. е. для каждой функции f Е Bh 2 нам известен набор g Е R q , q = P lN - )¹ N (l, d) такой, что

| Kf kl — g kl | 6 6 kl , l = 0,...,N — 1, k = 1,...,N(l,d).

В качестве методов восстановления рассмотрим отображения m : R q ^ L 2 ( B d ) . Определим погрешность метода

^e(Bh 2 ^,K,6,m) =     ^sup      ^k m⁽g) ^{— f} H l ₂ (B d )

f BBh2,

|Kfkl-gkl |6δkl и погрешность оптимального восстановления

E(Bh ₂ ,K,5) =     inf    e(Bh ₂ , K, 5, m).

m:R q ^ L ₂ (B ^d )

Теорема 3. Положим p N (l,d)

p = max j 0 6 p 6 N - 1 : X X S^l + 1) ² 6 1 к l=0 k=1

b          1          b     (l + 1)2

b = 2(p + 1) + d’ bki = 2l + d    b(l + 1) ’ l = 0,‘‘‘,p’ k = 1,---,N(l,d)i при S10 6 1’ или b = d bkl = 0’ l = 0’...’P’k = 1’...’N (l’d), при S10 > 1.

Тогда погрешность оптимального восстановления равна p N (M)

E(Bh 2 ’K’S) = tb +         ^b fci ^d 2l .

l =0 k =1

Метод

p N Vd                  / x ma(g)(x) =^2 52 akl(l + 1)g^l |x|l YU |X| )’ l=0 k=1                     \lxl/

где

λ kl

a kl = ~---------~—’

^{b (l + 1) 2 + b}kl

является оптимальным.

C Рассмотрим двойственную задачу kfkL2(Bd) ^ max’ f e Bh2’ lKfkll 6 Skl’ l = 0’...’N - 1’ k = 1’...’N (l’d).

Имеем оценку снизу

E ⁽Bh 2 ’K’5) >    SUp   ||f ||L2(B d ) .

f ∈ Bh 2 ,

| Kf kl | 6 δ kl

Переходя к квадратам функционала и ограничений и используя (9), перепишем задачу (23) в виде

^ N ( l,d ) ,, _|2               ^ N ( l,d )                  ., 2

EE 2^ - max. ££f kd² 6 1. (fL 6 » kl ’       (24)

l =0 k =1                     l =0 k =1

l = 0’...’N - 1’ k = 1’...’N (l’d).

Функция Лагранжа этой задачи имеет вид

N — 1 ^N(l,^d)             N — 1 ^N(l,^d) \ г \2 /                               I -i \2 \

\\         X X    д2    X X   \Jkl\          2        ^{(l +} 1)

^L(J’^b) = ^{- b -} 2_^ / v ^{b kl 6} kl ⁺           (l ₊ 1)2 ( ^{b(l +} 1) ^{+ b kl} — ₂l ₊ d )

l =0 k =1            l =0 k =1

^ N ( l,d )

+X X l=N k=1

f fk l ?

(l + 1) 2

b(l + 1) ² -

(l + 1П 2l + d /

где ^b = ^{{ b}’ ^b 10 ’ • • • ’ ^b N ( l,d ) N — 1 } .

Пусть J_w 6 1 , возьмем

Заметим, что

A=

2(p + 1) + d²

_       ( (l+1) ²

'   = {o 2'⁺d

-

—(l + 1) ,

l 6 p, p 6 N - 1.

A ki =

(l + 1) ²        (l + 1) ²

-

2l + d   2(p + 1) + d

> 0,

l 6 p.

Тогда при l 6 p

A(l + 1) ² + A ki - <2^

= 0.

При l > p

A—(l + 1)

-

(l + 1) ²

(l + 1) ²

2l + d 2(p + 1) + d

-

(-^ >  0.

2l + d

Таким образом,

----

.——

N - 1 N ( l,d )

L(b,A) > - A

-

E E A ki 5 2 = -a l=0 k=1

-

p N (M

E E A ki J 2i . l=0 k=1

Положим

^J kl ^{(l + 1)2}

fl = V¹ - P p P N^d W + D²2

0, l 6 p, l = p +1, l > p + 1.

Функция f(x) = P l°= ₀ P NE) f' ki lxl¹ Y ' (| X |) допустима в (24), так как

^ N ( l,d )                       _|2

ЕЕ If ki l ² = 1, 7f^2 - ^d 2 i = 0, l 6 p,k = 1,...,N (l,d). i =0 k =1                 ^{(l + 1) 2     ki}

Если p < N - 1 , то

^{| f} kp+1| / r2 (p + 2) ^{2 6 д kp+1 ,}

так как в противном случае имели бы P p+g¹ P N⁽1^d) ^ ki (l + 1) ² < 1, что противоречит определению p . Тогда

/ _ю N ( l,d )           \     N -1 N ( l,d )     /1—1         \

A EE& 1 ² - 1 + ЕЕ AkA fL -

\ l =0 k =1             /     l =0 k =1

и

N - 1 N ( l,d )                     p N ( l,d )

L(/, A) = - A - E E Ak^h = - A - E E A ki J 2i . l=0 k=1                 l=0 k=1

Следовательно, p N(l,d)

E(Bh 2 , K, J) >  t A + E E Aki5²_kl.

l =0 k =1

Пусть 6 1o > 1- Положим A = ( d , 0,..., 0). Тогда, очевидно,

----

L(f,A) >

- _d.

Функция f (x) = Y10(|X|) допустима в (24), удовлетворяет условиям дополняющей нежест- кости и L(f, A) =

— d , откуда следует

e (Bh 2 ,K,6) >  yd.

Для произвольного 6 рассмотрим метод ma, определенный в (21). При Akl = 0 из (22) следует, что akl = 0. Тогда sup f∈Bh2, |Kfkl-gkl |6δkl

Ilm o (g)

-

^f k L₂(B d ) ^{6 su} P kfkL, (B d ) ^{6 A} f ∈ Bh 2

В противном случае, имеем kma^) — fl^d) =

p N (M)

XX l =0 k=1

(a kl ^{(l + 1)g} kl ^— f kl )

2l + d

_ XNX (aki(l + 1)(gki l=0 k=1

-

fe) + f ki (a ki — 1)) ²

2l + d

Аналогично теореме 1 применим неравенство

p N (l,d)      , kma(g) — f kL2(Bd) 6 XX Akl (Akl(gkl l=0 k=1

где

A kl =

^ N ( l,d )

+ X X l=p+1 k=1

^ N ( l,d )

⁺ l=p+1 k=1

Коши — Буняковского.

-

¹    ( akl ^{(l +} 1)

2l + d

---ч λ kl

² f _kl

2l + d

f 2 f _kl

2l + d

.

Получим

,     ₉        x ^ N ( l,d )

fy + ^Af k²l) + X X

A    l=p+1 k=1

- +

^(a kl - ^{1) 2}

---4 λ

.

2 ^f kl

2l + d,

Равенства (22) эквивалентны равенствам A kl = 1 . при l >  p + 1 . Тогда

Заметим также, что 27+d

---4 λ ,

e(Bh k ,K, 6, m a ) ²

sup    I m ( g )

f ∈ Bh 2 ,

| Kf lk | 6 δ kl

-

^f k L ₂ (B d )

6 sup f ∈ Bh 2 , | Kf lk | 6 δ kl

p N (M)