Оптимизация геометрии составных упругих тел как основа совершенствования методик испытаний на прочность клеевых соединений

Идентификация параметров различных механических моделей или механических характеристик по большей части основана на использовании простых решений, которые, с одной стороны, исключают проблемы неединственности, имеющие место в обратных задачах, а с другой стороны, обеспечивают возможность и корректность измерения в физическом эксперименте соответствующих параметров. Под простыми решениями понимаются те из них, в которых реализуется однородное напряжённо-деформированное состояние. С достаточно обоснованной погрешностью подобное состояние наблюдается, например, в стандартном образце при испытаниях на одноосное растяжение или в трубчатом образце при растяжении, кручении, при нагружении внутренним давлением.

Анализ различных вариантов идентификации механических характеристик материалов показывает, что предположение об однородности напряжённого состояния при простом нагружении не всегда отвечает действительности. В частности, такая ситуация имеет место при определении прочности клеевых соединений на отрыв и сдвиг.

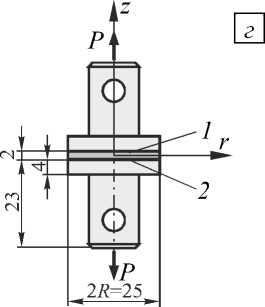
Это подтверждается вычислительными экспериментами над установленными действующими ГОСТами образцами для испытаний: образец А — ГОСТ 14760-69 «Клеи. Методы определения прочности при отрыве» (Рис. 1, а ), образец Б — ГОСТ 14759-69 «Клеи. Методы определения прочности при сдвиге» (Рис. 1, б ), образцы В и Г — ГОСТ 209-75 «Клей и резина. Методы определения прочности связи с металлом при отрыве» (Рис. 1, в , г ). Согласно этим ГОСТам прочность при отрыве и сдвиге определяется по формуле: а = P/F, где P — разрушающая сила, F — площадь склеивания.

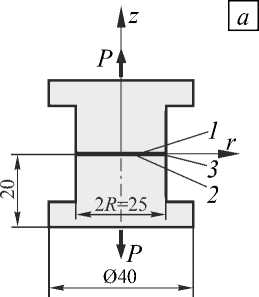
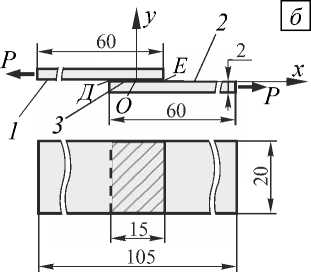
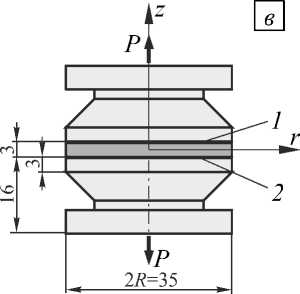
Рис. 1. Стандартные образцы для определения прочности клеевых соединений (размеры в мм); 1 и 2 – поверхности сопряжения, 3 – клеевой слой

В математической теории упругости известны сингулярные решения задач, связанные с бесконечными значениями напряжений в точках поверхности (особых точках), где имеет место нарушение её гладкости, смена типа краевых условий или контакт различных материалов. Поскольку в рассматриваемых образцах подобные точки присутствуют, распределение отрывных и сдвиговых напряжений по поверхности склеивания может быть неоднородным. Из работ [1–4], связанных с построением и исследованием сингулярных решений, для данной работы имеют значение следующие положения и результаты: сингулярные решения, полученные в рамках линейной теории упругости для идеализированной геометрии и граничных условий, отражают присутствие в реальном моделируемом объекте ярко выраженной концентрации напряжений; наличие сингулярного решения и его характер в окрестности края поверхности соединения двух материалов определяются геометрией тела и значениями упругих постоянных. Они позволяют сделать заключение о том, что устранение концентрации напряжений в окрестности особых точек связано с выбором геометрии и значений упругих постоянных, при которых решение не имеет сингулярного характера. Это послужило основой для обобщения, названного явлением малонапряжённости [5]. В [6, 7] рассмотрен более общий случай, а именно решается оптимизационная задача поиска геометрии и упругих постоянных в окрестности особой точки, обеспечивающих оптимальное по заданному критерию напряжённо-деформированное состояние.

Имеется серия работ, в которых задача снижения уровня напряжений в окрестности особых точек, направлена на совершенствование методик испытаний и повышение прочности клеевых соединений. Например, в [8] на основе численного и экспериментального моделирования найдены варианты соединения различных материалов в образцах цилиндрической и призматической формы, в которых отсутствует концентрация напряжений на поверхности соединения. В [9] для повышения прочности клеевых соединений предлагается поиск наилучшего угла косого соединения встык различных материалов.

В настоящей работе рассматривается задача оптимизации, направленная на поиск геометрии тела, обеспечивающей близкое к однородному распределение напряжений на границе соединения различных материалов. Приводятся результаты численного анализа напряжённого состояния в стандартных образцах (Рис. 1) и даются рекомендации по совершенствованию их геометрии.

• 2.    Численный анализ напряжённого состояния стандартных образцовдля испытаний клеевых соединений

Численные результаты, характеризующие напряжённо-деформированное состояние в стандартных образцах для испытания прочности клеевых соединений, получены на основе метода конечных элементов. Для достижения необходимой точности расчётов в окрестности особых точек использовались два алгоритма. В одном из них по мере приближения к особой точке сгущалась сетка стандартных конечных элементов, а в другом в окрестности особых точек сетка включала сингулярные конечные элементы [10].

Эффективной оценкой точности полученных численных результатов при решении задачи на основе принципа возможных перемещений является погрешность выполнения естественных краевых условий на свободной от нагрузок боковой поверхности образцов и на поверхности контакта различных материалов. Эта погрешность определяется соотношениями ст JP , т n/ P на свободной поверхности и соотношениями ( с П -ст 2 )/ P , ( T n - т 2 )/ P на поверхности контакта. Здесь ст n , т n — нормальные и касательные напряжения на соответствующих поверхностях; верхний индекс указывает на принадлежность одному из двух контактирующих материалов, Р — внешняя нагрузка. В проведённых расчётах погрешность выполнения естественных краевых условий составляла менее 1%.

Для образцов А и Б имеет смысл рассматривать характер распределения напряжений только с учётом клеевой прослойки толщиной t. На рисунке 2, а приведено распределение отрывных напряжений по поверхности контакта материал–клей образца А для двух значений толщины клеевого слоя. В данном случае сингулярность решения проявляется в том, что распределение напряжений в окрестности края поверхности контакта материал–клей имеет существенно неоднородный характер, а на её краю напряжения асимптотически стремятся к бесконечности при увеличении числа конечных элементов. Практически это означает, что окрестность края поверхности контакта материала и клея является зоной ярко выраженной концентрации напряжений. Размеры этой зоны зависят от толщины клеевого слоя. Рисунок 2, б демонстрирует распределение касательных напряжений на верхней границе контакта материал–клей для образца Б. Следует отметить, что несимметрия относительно точки О (x = 0) обусловлена тем, что на левом краю поверхности склеивания угол между внешними поверхностями клея и материала равен п/2 (см. угол с вершиной в точке Д), а на правом — п (см. угол

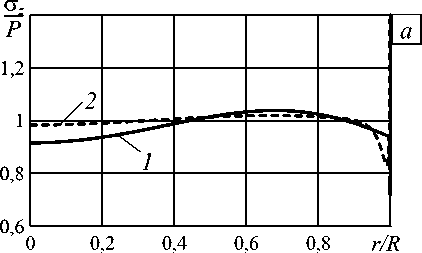
Рис. 2. Распределение напряжений по поверхности контакта материал–клей в образцах А ( а ) и Б ( б ) с учётом толщины клеевого слоя t , мм: 0,01 (кривая 1 ); 0,5 ( 2 ); 0,15 ( 3 )

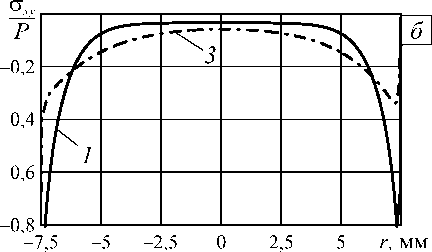
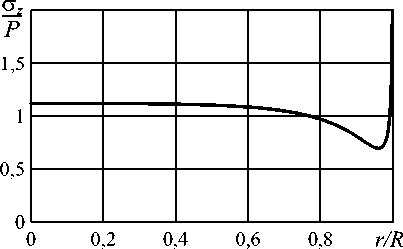
Рис. 3. Распределение отрывных напряжений по поверхности контакта металл–резина в образце В с вершиной в точке Е). Расчёты выполнены при следующих значениях механических характеристик материала и клея: Eм = 2,1-1011 Па, vM = 0,3, Eк = 4,0 -109 Па, vк = 0,3.

Для образцов В и Г расчёты напряжённо-деформированного состояния проведены без учёта клеевой прослойки. Рисунок 3 содержит кривую распределения отрывных напряжений в образце В при следующих значениях параметров металла и резины: E _м = 2,1 - 10¹¹ Па, v _м = 0,28 , E _р = 1,667 - 10⁷ Па, v _р = 0,4. Распределения отрывных напряжений в зависимости от безразмерного радиуса r / R в образцах В и Г совпадают. Приведённые результаты расчётов демонстрируют, что во всех рассмотренных образцах распределение напряжений, по которым оценивается прочность клеевого соединения, имеет существенно неоднородный характер.

• 3.    Оптимизация геометрии составных упругих тел в окрестностикрая поверхности контакта двух материалов

Один из возможных путей получения более однородного распределения напряжений в образцах для определения прочности клеевых соединений связан с поиском новой геометрии образцов. Рассмотрим задачу оптимизации для кусочнооднородного тела объёмом V = V1 + V2, ограниченного поверхностью 5 = 5 1 + 52. Здесь нижние индексы обозначают принадлежность одному из материалов. В данном случае точки соединения поверхностей S1 и S2 являются особыми точками, поскольку в них имеет место контакт двух материалов.

Для решения оптимизационной задачи вводится функционал

F (5f )=

^С о

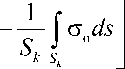
ds ,

который определяет среднеквадратическую невязку отклонения нормальных напряжений со на поверхности контакта 5k материалов от их среднего значения на этой поверхности. Здесь Sf

—

часть поверхности S в окрестности особой точки.

На поверхность S f могут быть наложены ограничения типа равенств и неравенств:

XG Я* X

X S f X ,

;

Требуется найти поверхность

^{X X          X        X} \

X G V f* ( X ) , S f ( X ) C V f ( X ) .

S f , удовлетворяющую ограничениям

минимизирующую функционал (1), либо обеспечивающую его значение некоторой заданной величины.

При численной реализации поставленной оптимизационной задачи

(2) и меньше

решение

отыскивается на ограниченном классе поверхностей. В качестве образующих для таких поверхностей могут использоваться кусочно-полиномиальные или другие функции, найденные по значениям координат или производных рассматриваемой функции в конечном числе узловых точек. Тогда часть геометрии тела S f определяется конечным числом параметров, а функционал (1) превращается в функцию этих параметров. В этом случае задача оптимизации функционала (1) при ограничениях (2) сводится к минимизации функции конечного числа переменных, то есть к классической задаче нелинейного математического программирования. Расчёт напряжённого состояния на каждом шаге численной процедуры решения задачи нелинейного математического программирования осуществляется методом конечных элементов.

б

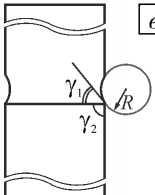
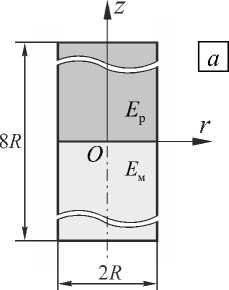
Рис. 4. Составной цилиндр с исходной ( а ), оптимальной ( б ) и технологичной ( в ) формой боковой поверхности

Далее в качестве примера приводится решение задачи поиска оптимальной геометрии составного цилиндра (Рис. 4, а). Геометрия боковой поверхности образца в окрестности особой точки аппроксимировалась кубическими кривыми, которые определялись значениями координат и их производных в двух узловых точках. На оптимизируемую геометрию накладывались ограничения, при которых площадь склеивания оставалась постоянной. Механические соответствовали образцу В.

характеристики материалов

точки зрения минимальности в окрестности особых точек

В работах [6,7] показано, что оптимальная (с интенсивности касательных напряжений) геометрия определяет границу между решениями с сингулярностью и без сингулярности. Это свойство оптимальных поверхностей получило подтверждение и в задачах оптимизации геометрии составного тела в окрестности края поверхности соединения двух материалов. Поясним это на рассматриваемом примере.

Анализ характера поведения напряжений в окрестности особой точки поверхности, где имеет место соединение двух материалов, при плоско-деформированном состоянии опирается на решение задачи исследования собственных решений для составного клина [11, 12], который образован касательными к поверхности тела в особой точке (см., например, Рис. 4, б). Собственные решения в полярной системе координат с центром в вершине клина имеют следующий вид:

u (r, ф) = rX k L(k )(ф), где собственные значения Xk находятся из уравнения

	1 0 0	0 1 0	-(X + 1 ) 0 - ( a+ 1 )	0 X- 1 0	- 1 0 P-a	0 - 1 0	X+ 1 0 1 -P+X ( a-p )	0 1 -X 0
det	0 cos a 1	0 sin a 1	0 - ( X+ 1 ) cos b	- ( a+ 1 ) ( X+ 1 ) sin b	0 0	P-a 0	0 0	1 -p+X ( p-a ) 0	= 0. (3)
	- sin a	cos a 1	( X- 1 ) sin b	( X- 1 ) cos Z t,	0	0	0	0
	0	0	0	0	sin a 2	cos a 2	( l -X ) sin b 2	( X- 1 ) cos b 2
	0	0	0	0	- cos a 2	sin a 2	( 1 +X ) cos b 2	( X + 1 ) sin b 2

Здесь a i = ( X + 1 ) у i , b i = ( X- 1 ) у i ,

г(ki +1)-(k2 + 1) и в = г(ki -1)-(k2 - 1) г(k1 +i)+(k2+1) и Р~Г(k, +1)+(k2 +1)

комбинированные параметры упругих постоянных материалов [13], где k i = 3 - 4 v i , Г = G ₂ /G₁, G i = E i /2 ( 1 + v i ) , ( v i , G i — коэффициенты Пуассона и модули сдвига материалов), i = 1, 2.

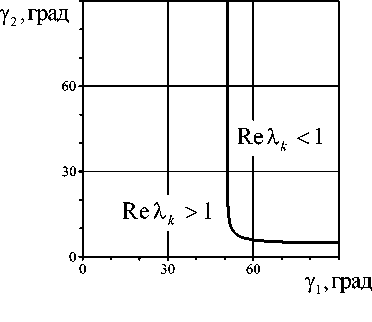
Рис. 5. Кривая Re X _k = 1, разделяющая решение в плоскости параметров у ₁ и у ₂ на сингулярное и несингулярное

Из соотношения (3) следует, что собственные значения зависят от величин углов у ₁, у ₂ и механических характеристик v ₁, v ₂ , E ₁ / E ₂ . Если среди собственных значений

Xk отыщутся такие, действительная часть которых меньше единицы (0 < Re Xk < 1), то решение в особой точке будет иметь сингулярный характер. Для конкретных материалов в плоскости параметров у1 и у2 может быть построена кривая Re Xk = 1, которая разделит область решений на две подобласти: с сингулярностью и без нее. В частности, для рассматриваемого примера такая кривая представлена на рисунке 5.

Картины распределения напряжений для геометрий, соответствующих разным точкам кривой Re Xk = 1, отличаются, но незначительно. Эта неединственность устраняется при обеспечении достаточной точности расчёта напряжённого состояния в процессе оптимизационного поиска. Оптимальный вариант геометрии будет соответствовать точке кривой Re X k = 1 , имеющей наибольшее значение угла между поверхностью контакта и боковой поверхностью более жёсткого материала (в данном случае угла у2). Значения углов у1 и у 2, определяющие оптимальную поверхность, соответствуют только одной точке на кривой Re X k = 1. На рисунке 6 приведены распределения отрывных напряжений по поверхности контакта в исходном и оптимальном образцах. Путём варьирования у1 и у 2 в рассматриваемой задаче удаётся устранить концентратор

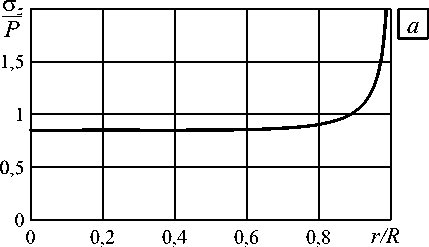
Рис. 6. Распределение отрывных напряжений на поверхности контакта в исходном ( а ) и оптимальном ( б ) образцах

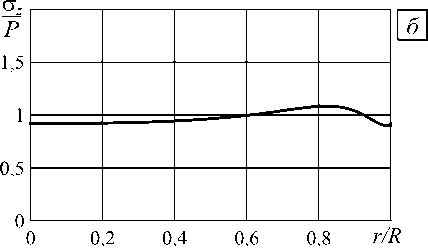
напряжений и получить достаточно равномерное распределение отрывных напряжений на поверхности контакта.

Численные эксперименты по оптимизации геометрии составных тел в окрестности края поверхности соединения двух материалов показали, что использование различных видов функций, аппроксимирующих свободные боковые поверхности в окрестности особых точек, приводит к различным вариантам геометрии, которые, незначительно отличаясь, обладают общим признаком: оптимальные значения параметров γ ₁ , γ ₂ , ν ₁ , ν ₂ , E ₁ / E ₂ находятся на границе между решениями с сингулярностью и без сингулярности. Используя это свойство, можно получить наиболее однородный характер напряжений на поверхности склеивания, не решая оптимизационную задачу.

Изготовление образцов с геометриями, найденными путём решения оптимизационной задачи, может иметь определённые технические трудности. В связи с этим при совершенствовании геометрии образцов для испытания клеевых соединений предлагается: использовать свойство оптимальных геометрий в окрестности особых точек упругих тел; выбирать для изготовления простую (технологичную) геометрию образца.

Наиболее подходящим (технологичным) является следующий вариант геометрии образцов для испытания клеевых соединений на отрыв: в окрестности края поверхности клеевого соединения форма боковой поверхности менее жёсткого материала (в данном случае резины) представляется дугой окружности, центр которой выбран таким образом, чтобы угол сопряжения этой дуги с поверхностью склеивания соответствовал кривой Re λ _k = 1 (см. Рис. 4, в ). Величины напряжений в оптимальном (Рис. 6, б ) и технологичном образцах отличаются в пределах 1%, что позволяет сделать заключение об эквивалентности этих образцов для использования в реальных экспериментах.

• 4.    Выводы

Выполнено численное исследование напряжённого состояния в образцах, установленных ГОСТами для испытания на прочность клеевых соединений, которое показало существенную неоднородность распределения отрывных или сдвиговых напряжений по поверхности склеивания.

Предложена и численно решена задача оптимизации геометрии составного тела в окрестности края поверхности соединения двух материалов, целью которой было получение достаточно однородного распределения напряжений на поверхности контакта. Анализ решений оптимизационных задач выявил общее свойство у оптимальных поверхностей, состоящее в том, что параметры оптимальной геометрии в точке контакта двух различных материалов, как показывает решение соответствующей задачи для составного клина, лежат на границе между решениями с сингулярностью и без сингулярности. На основе выполненных исследований сформулированы рекомендации по изготовлению образцов для испытаний клеевых соединений, обеспечивающие с практической точки зрения достаточно однородное распределение напряжений на поверхности склеивания.

Работа выполнена при финансовой поддержке РФФИ (проект № 11-01-96017-р_Урал_а) и Совета по грантам Президента РФ для молодых российских учёных (грант № МК-5286.2010.1).