Оптимизация маршрутов полета беспилотных летательных аппаратов при местоопределении источника радиоизлучения по оценкам угловых координат с их бортов

Для повышения достоверности контроля сложной радиоэлектронной обстановки в комплексах мониторинга на беспилотных летательных аппаратах (БЛА) требуется применять высокоточные методы местоопределения источников радиоизлучения [1]. Данные о координатах позволяют выполнять распознавание объектов при реализации мер маскировки, повышенной скрытности работы, использовании сигналов с адаптивно изменяющимися и перекрывающимися по значениям частотно-временными параметрами [1; 2].

Местоположение передатчиков сигналов большой длительности с характерными демаскирующими признаками [2] можно определять по результатам пеленгования в различных точках пространства на маршруте полета БЛА [1; 3]. Для оценки координат источников коротких (сверхкоротких) импульсов и излучателей с малым набором параметров идентификации [2] необходимо применять триангуляционный метод [4] при синхронном функционировании приемников-пеленгаторов, размещенных на бортах двух носителей, барражирующих в заданных позиционных районах [1].

При этом движение БЛА должно осуществляться по траекториям, выбираемым из условия обеспечения требуемой точности местоопре-деления объектов наличии эксплуатационных погрешностей измерения углов прихода сигналов [3].

В предлагаемой работе представлены алгоритмы минимизации среднеквадратической ошибки (СКО) оценки координат наземных источников радиоизлучения за счет выбора точек их пеленгования с бортов одиночного БЛА и двух носителей приемников-пеленгаторов из состава триангуляционной системы.

Цель работы – достижение наилучшей точности местоопределения излучателей за счет оптимизации маршрутов полета БЛА.

• 1.    Оптимизация маршрута полета беспилотного летательного аппарата при местоопределении объектов по многократным оценкам угловых координат

  Будем полагать, что источник радиоизлучения расположен в начале полярной системы координат ( R , ф ) и в процессе выполнения измерений остается неподвижным; позиции, в которых определяются направления прихода сигналов в последовательные моменты времени t n и t n ₊ i , n = 1, 2, 3 …, характеризуются наклонными дальностями R n и R n _{+ 1}, n = 1, 2, 3 ... Величины R n и R n _{+ 1}, n = 1, 2, 3 ^, значительно превышают высоту полета БЛА и дистанцию L между точками пеленгования. Полет БЛА на интервале времени © Разиньков С.Н., Богословский А.В., 2015

t n + 1 - t n осуществляется под курсовым углом Y _n , n = 1, 2, 3 ..., отсчитываемым от направления на излучатель в момент времени t n , n = 1, 2, 3 …, против часовой стрелки; направление у 1 определяется относительно ф = 0. Пространственное положение приемника-пеленгатора относительно источника радиоизлучения определяется по результатам пеленгования и данным аппаратуры навигационно-временного обеспечения [5] в бортовом решающем устройстве, построенном на основе линейного фильтра [1; 6].

Систематические погрешности фиксации угла места, тангажа и крена БЛА малы относительно СКО пеленгования сигналов ст и ст , n = 1, ф n     ф ( П + 1 )

2, 3 …; погрешностями позиционирования приемников-пеленгаторов при определении дисперсии оценки местоположения излучателя ct R можно пренебречь.

Время корреляции траекторной нестабильности БЛА в полете [5] существенно меньше длительности обрабатываемых сигналов, поэтому измерения в бортовых приемниках-пеленгаторах выполняются без аномальных ошибок [3; 6].

Оптимизация маршрута полета БЛА для достижения наилучшей точности местоопределения источника радиоизлучения состоит в нахождении направления движения у n , n = 1, 2, 3 ... в момент времени t _n , n = 1, 2, 3 ... по критерию

• у n = arg min CT r ;

^Y n                                          ⁽¹⁾

Y _n *п m , n = 1,2,3 ..., m = 0,1,2 ...

Второе уравнение в (1) исключает из рассмотрения направление движения БЛА непосред- ственно на источник радиоизлучения, поскольку его угловые координаты априори неизвестны [3].

Дисперсия оценки местоположения излучате ля имеет вид [4]

22  2    2

• 2 _ ^стф n R n ^{+ СТ}ф ( n + 1 ) R n + 1

^CT R =                ₉                 , n = 1, ², ³ •••, ⁽²⁾

sin2 9 n где 9 n — угловое расстояние между пеленгами, измеренными в моменты времени tn и tn+1, n = 1, 2, 3 …

Согласно теореме синусов [7], sin 9n = —— sin Yn, n = 1, 2, 3 •••;           (3)

R n + 1

в соответствии с теоремой косинусов [7] наклонные дальности Rn и Rn+1, n = 1, 2, 3 ... связаны соотношением

R 2n _{+ 1} = R 2n + L ² - 2 R_nL cos Y _n , n = 1, 2, 3 ... (4)

В результате подстановки (3), (4) в (2) находим

2    22   2       2   2

^ст R ( ^стф n^Rn ^{+ ст}ф ( n + 1 ) ( ² R n ^{+ L}

• - 2 R_nL cos y _n ) ) ( R 2 _n + L ² - 2 R_nL cos y _n ) /     (5)

  / L ² sin² Y n

Минимальная дисперсия местоопределения объекта достигается для курсового угла БЛА Y _n , n = 1, 2, 3 ..., при котором первая производная (5) обращается в нуль. С учетом условия Y _n * п m , n = 1, 2, 3 ..., m = 0, 1, 2 ... при a _n = R_n / L >> 1

направление движения в момент времени t n , n = 1, 2, 3 ... удовлетворяет уравнению cos2 Yn - вn cos Yn + 1 = 0, n = 1, 2, 3 ...,       (6)

где в n = [( стф n + стф( n + 1)) a n +

⁺ ( ^{2 ст}ф n ^{+ 5 ст}ф ( n + 1 ) ) ^a 2 n ^{+ ст}ф ( n + 1 ) ] /

/ [ ( ^стф n ^{+ 2 ст}ф ( n + 1 ) ) ^a 3 n ^{+ 2 ст}ф ( n + 1 ) ^a n n = 1, 2, 3 _

На основе решения (6) имеем:

Y _n = ± arccos

i n __ V^e n ^{4 2}

V               7

+ 2п m ,

n = 1, 2, 3 .„, m = 0,1, 2.„

Знак обратной тригонометрической функции и число m выбираются таким образом, чтобы угол Y _n , n = 1, 2, 3 ^ принадлежал полупространству с вертикальной границей вдоль продольной строительной оси БЛА, в котором расположен пеленгуемый источник радиоизлучения. На практике неоднозначность решения (8) устраняется путем селекции направлений прихода сигналов по бортам носителя в многошкальных измерителях с неэквидистантными антенными решетками или пеленгаторов с секторными антеннами [8].

Из (7) следует, что при равных значениях СКО пеленгования сигналов в моменты времени t_n и t_{n +} 1 , n = 1, 2, 3 ^ курсовой угол БЛА определяется выражением (8), в котором [3]

2a n + 7a n + 1 a n ( 3a n + 2 )

n = 1, 2, 3 _

На рис. 1 приведены найденные с использованием (7), (8) траектории движения БЛА относительно объекта при исходном значении наклонной дальности R ₁ = 30 км, при СКО пе-

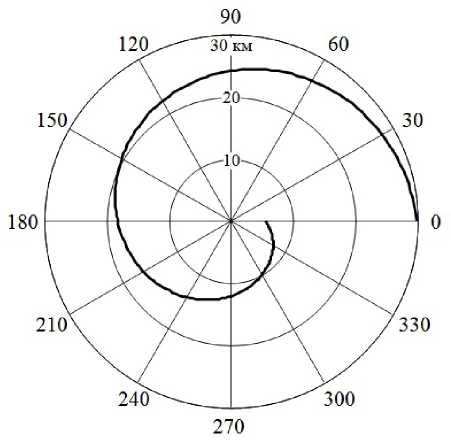
Рис. 3. Маршрут полета БЛА при дисперсии оценки угловых координат объекта о , n = о , ( n _{+ 1} ) , n = 1, 2, 3 —

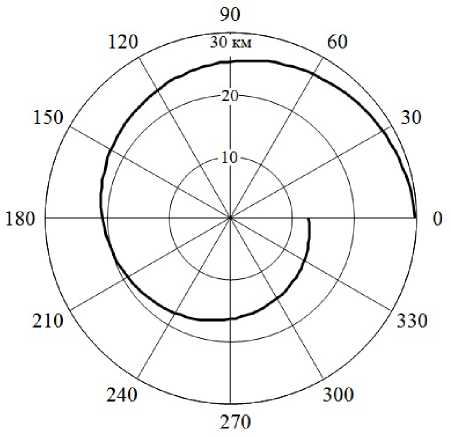
Рис. 1. Маршрут полета БЛА при изменении дисперсии оценки угловых координат объекта по закону о , n / о , ( n +ц = 2, n = 1, 2, 3 —

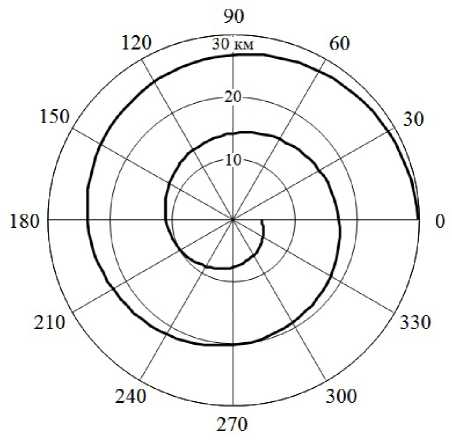
Рис. 2. Маршрут полета БЛА при изменении дисперсии оценки угловых координат объекта по закону о , ( n _{+ 1} ) / о , n = 2, n = 1, 2, 3 —

ленгования сигналов о , 1 = 10° с тенденцией изменения точности последующих измерений ^о, n / ^о, ( n + 1 ) = ^2, n = 1, ^{2, 3} - ^На Р^ис. ^{2 п}РеД— ставлены результаты, полученные при о , 1 = 1° и закономерности увеличения дисперсии оценки угловых координат источника радиоизлучения вида о , ( n + 1 ) / о , n = 2, n = 1, 2, 3 — Снижение точности пеленгования при подлете к объекту возможно вследствие уменьшения уровня боковых лепестков диаграммы направленности его антенны, по которым осуществляется перехват сигналов в точках пространства, разнесенных в азимутальной плоскости на угол у n , n = 1, 2, 3 —

Анализ приведенных результатов показывает, что наилучшая точность определения местоположения источника радиоизлучения достига- ется при движении носителя приемника-пеленгатора по траектории в виде спирали. Изменение курсового угла, определяемое значениями дисперсии оценки угловых координат излучателя, возрастает относительно начального значения по мере уменьшения наклонной дальности Rn , n = 1, 2, 3 — За счет повышения точности пеленгования при приближении к объекту сжатие спирали уменьшается. При этом протяженность маршрута полета БЛА на рис. 2 превышает длину траектории движения на рис. 1 примерно в 1,7 раза.

На рис. 3 приведен маршрут полета БЛА, проложенный с использованием (8), (9), при равной точности пеленгования излучателя в моменты времени t_n , n = 1, 2, 3 — Согласно (9), траектория движения БЛА не зависит от СКО оценки угловых координат излучателя; точность оценки 22

его местоположения при о , n = о , ( n + 1 ) , n = 1, 2, 3 …, определяется дальностью до приемно-пеленгационного поста. При уменьшении СКО пеленгования сигналов с 10° до 1° протяженность маршрута полета БЛА сокращается в 1,4 раза.

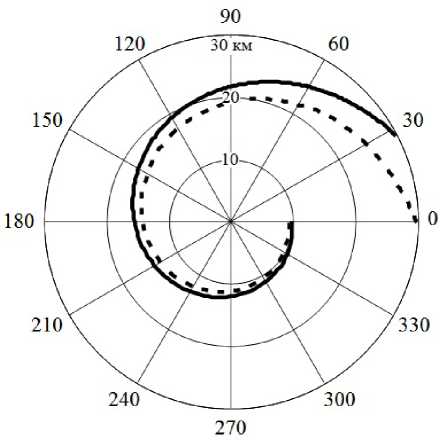
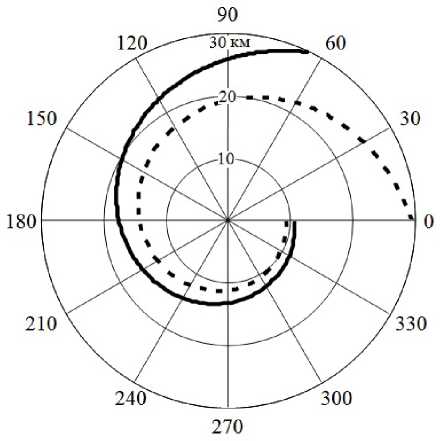
На рис. 4 представлены траектории движения БЛА при местоопределении излучателя по оценкам его угловых координат с СКО о , _n = 1° в секторе углов , е [0; 180°) и о , _n = 10° в секторе углов , е [180°; 360°), n = 1, 2, 3 —, а на рис. 5 - результаты при о , _n = 10° в секторах углов , е [0; 180°) и о , _n = 1° в секторе углов , е [180°; 360°), n = 1, 2, 3 …

Согласно приведенным зависимостям, маршрут полета БЛА существенно зависит от дисперсии ошибки оценки угловых координат объекта в начальный момент времени. При этом, несмо-

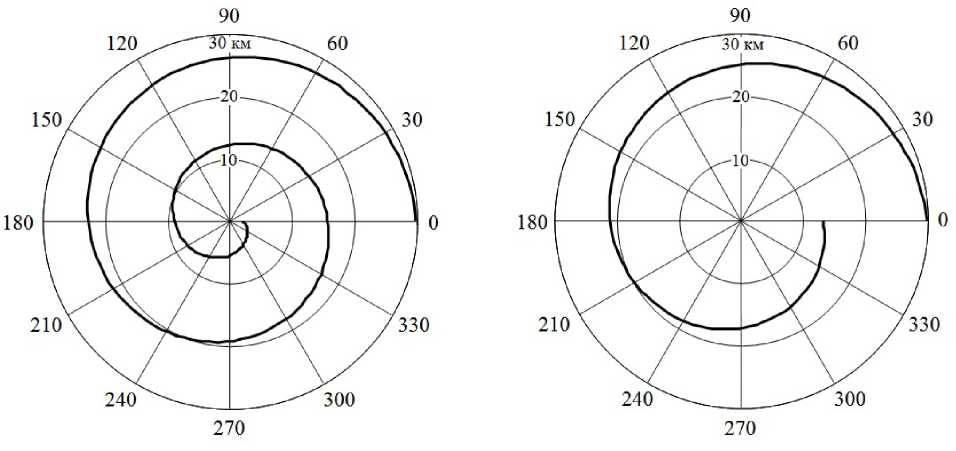
Рис. 5. Маршрут полета БЛА при СКО пеленгования объекта С ф n = 10 ° в секторе углов фе [0; 180 ° ) и С ф n = 1 ° в секторе углов ф е [180 ° ; 360 ° )

Рис. 4. Маршрут полета БЛА при СКО пеленгования объекта С ф n = 1 ° в секторе углов ф е [0; 180 ° ) и С ф n = 10 ° в секторе углов ф е [180 ° ; 360 ° )

тря на различие точности измерений в секторах углов, для траектории движения нехарактерна значительная асимметрия ввиду свойства спирали восстанавливать свою форму после воздействий [9].

Q n = arctg

f — 1 . 2p n ,

+ n m, p n

R n d ^,

n = 1, 2, 3 ..., m = 0, 1, 2 ...;

2. Оптимизация маршрутов полета двух беспилотных летательных аппаратов при местоопределении объектов по результатам синхронного пеленгования

угловое расстояние относительно центра системы координат между точками пеленгования

<) = 9 n +(-1)k+1 Q n +(-1)k Q n+1, n = 1, 2, 3 ..., а дистанция

Будем полагать, для местоопределения источника радиоизлучения выполняются синхронные измерения его угловых координат с бортов двух БЛА, барражирующих на удалении d друг от друга, в моменты времени t _n , n = 1, 2, 3 ^ Наклонная дальность R_n , n = 1, 2, 3 ^ определяется как расстояние между объектом и центральной точкой пеленгационной базы; ее величина значительно превышает d , смещение центра пеленгационной базы L и дистанцию L ⁽ k ) , преодолеваемую к- м носителем, к = 1, 2, за интервал времени t n + 1 - t n , n = 1, 2, 3 ^

Для минимизации дисперсии оценки координат излучателя c R пеленгационная база ориентирована перпендикулярно линии, по которой измеряется наклонная дальность. При этом курсовые углы БЛА y n^k ) , к = 1, 2, n = 1, 2, 3 ^ определяются на удалении от объекта

L ⁽ k ) = V R 2n + R 2n + 1 - 2 R n R n + 1 cos 9 n ) , к = 1,2, n = 1,2,3

Ввиду того, что a _n >> 1, n = 1, 2, 3 ...,

траек-

тория движения центра пеленгационной базы удовлетворяет (8). Курсовые углы носителей приемников-пеленгаторов у^ ) , к = 1, 2, n = 1, 2, 3 … по аналогии с (3) удовлетворяют соотношению

sin Y nk )

к = 1, 2,

Из (12),

R n

Rn            , cos Qn

где

/-V

Rn+1      ( k )

L ( к ) ^{s 9 n} ,

n = 1, 2, 3 ...

(13) с учетом (10), (11) находим, что

направление движения k-го БЛА, к = 1, 2 в момент времени t n, n = 1, 2, 3 ... соответствует главному значению аргумента функции ctg Ynk) =

sin (9n +(-1)k+1 Q n +(-1)k Q n+1)

R n cos ^Q n + 1 ^x ----------- +

R_{n + 1} cos Q

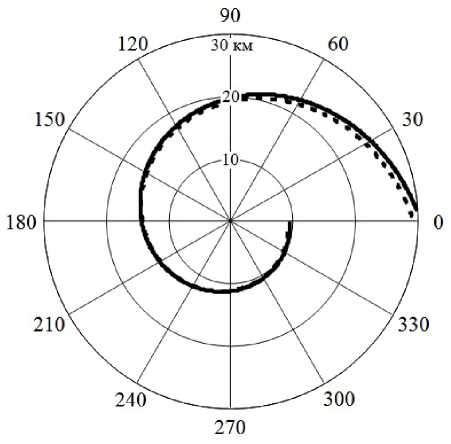
Рис. 6. Маршруты полета БЛА при местоопределении объектов триангуляционной системой с пеленгационной базой d = 2 км —

+ ctg ( э n + ( -1 ) k ^{+ 1} Q n + ( -1 ) k Q n + 1 ) .

Правило выбора знака перед первым слагаемым аналогично использованному при устранении неопределенности решения (8); знаки «–» и «+» перед функцией ctg ( ... ) определяют траектории движения БЛА, смещенные относительно центра пеленгационной базы на - d 2 и d /2 соответственно.

На рис. 6 приведены маршруты полета БЛА при триангуляционном местоопределении излучателей с пеленгационной базой d = 2 км; на рис. 7 — с базой, при которой a _n = 10 ( а ) и а _n = 5 ( б ). Штриховой линией представлены траектории, построенные при выборе перед функцией ctg ( ... ) знака «—», сплошной — знака «+».

Из представленных результатов следует, что существенное различие маршрутов полета БЛА при постоянной и варьируемой пеленгационной базе наблюдается на значительном (свыше 20 км) удалении от источника радиоизлучения. По мере приближения к объекту влияние размеров базы на траектории движения БЛА, определяемые по критерию (1), снижается.

Заключение

Таким образом, проведена оптимизация маршрутов полета БЛА с бортовыми приемниками-пеленгаторами, для обеспечения наилучшей точности местоопределении наземных источников радиоизлучения при различных СКО измерений углов прихода сигналов в точках пространства выполнена оптимизация. Найдены правила выбора позиций пеленгования объектов и проведен

а )

б )

Рис. 7. Маршруты полета БЛА при местоопределении объектов в триангуляционной системе с параметром a n = 10 ( а ) и ^а n = ^{5 (} б )

анализ траекторий движения одиночного БЛА и курсовых углов двух синхронно барражирующих носителей приемников-пеленгаторов из состава триангуляционной системы.