Оптимизация параметров магнито-резонансных томографов

Магнито-резонансная томография (МРТ-томография) в настоящее время является наиболее популярным методом визуализации внутренних органов при диагностике различных заболеваний [1–7]. В этом методе, прежде всего, исследуется распределение концентрации атомов водорода в различных водородосодержащих тканях организма.

Основная идея метода заключается в возбуждении резонансной прецессии магнитных моментов ядер атомов водорода (протонов), находящегося в постоянном магнитном поле. Резонансной, т. к. частота прецессии совпадает с частотой возбуждающего эту прецессию переменного магнитного поля. В дальнейшем осуществляется регистрация ЭДС электромагнитной индукции, возникающей в катушке, рис. 1, находящейся в

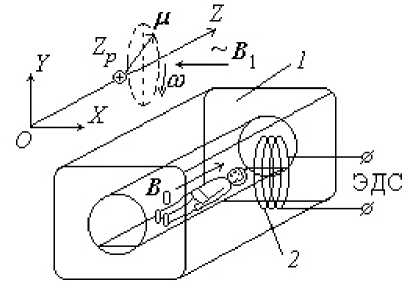
Рис. 1. Схема диагностического процесса в магнито-резонансном томографе области воздействия магнитного поля прецессирующего магнитного момента протона . В физике это явление носит название ядерного магнитного резонанса (ЯМР).

Циклическая частота прецессии определяется формулой Лармора:

ю = Y B, µ где γ= – постоянная для данного химическо го элемента величина – т. н. гиромагнитное отношение; магнитный момент протона нормированный на приведенную постоянную Планка равен µp          8 1                     -26 Дж

µ= =1,34 ⋅10       , где µ=1,406 ⋅10

Й ^,          Тл■с, p ^,              Тл

– абсолютный магнитный момент протона.

Целью настоящей работы является выяснение оптимального соотношения, с точки зрения качества визуализации, наиболее существенных параметров прецессирующего протона, как-то угла прецессии, частоты прецессии и внешних постоянного и переменного магнитных полей.

1. Магниторезонансный томограф

Схема магниторезонансного томографа представлена на рис. 1.

Пациент помещается в корпус томографа ( 1 ) на подвижной кушетке. В томографе, с помощью катушек, не показанных на рис. 1, создаются постоянные (не меняющиеся со временем) магнитные поля в направлении всех трех осей OX , OY , и OZ . На рис. 1 показано основное постоянное магнитное поле В о , направленное вдоль © Волобуев А.Н., 2016

оси Z . Вдоль этой оси располагается пациент. Постоянные магнитные поля изменяются линейно вдоль осей, т. е. носят градиентный характер. Зависимость индукции основного постоянного магнитного поля, например, от координаты Z имеет вид:

B0 = kZ, где k – коэффициент пропорциональности.

Магниторезонансный томограф обычно работает в импульсном режиме. Это означает, что соленоид ( 2 ) на рис. 1 (радиочастотная катушка) подает импульсы переменного магнитного поля B ₁, которое разворачивает магнитные моменты ядер исследуемого элемента в организме и они начинают вращаться (прецессировать) под некоторым углом 9 к оси Z — углом прецессии. Во время паузы в этом же соленоиде наводится, за счет явления электромагнитной индукции, ЭДС (МРТ-сигнал), которая подается на ЭВМ для формирования МРТ-изображения.

Частота подаваемого импульсного сигнала будет вызывать резонансную (той же частоты) прецессию магнитного момента ядра со значительным углом прецессии 9 только на определенной координате Z_p . Действительно, если в формулу Лармора для частоты прецессии подставить зависимость индукции постоянного магнитного поля от координаты, то получим:

to = уBo = уkZ .

Следовательно, подавая определенную частоту to переменного магнитного поля B i на организм, мы, фактически, выбираем, при заданном Y (т. е. выбранном элементе, распределение которого исследуется), определенное, соответствующее этой частоте, сечение организма Z_p , с которого регистрируется МРТ-сигнал. Задание величины Y определяется допустимым диапазоном частот to переменного магнитного поля В 1 , генерируемого радиочастотной катушкой ( 2 ), рис. 1. Этот диапазон частот Ato = у A B o определяет создаваемый градиент индукции основного магнитного поля В о . Если частота to выходит за допустимый диапазон, то начинает возбуждаться резонансная прецессия магнитных моментов ядер элементов с другим значением гиромагнитного отношения у, что недопустимо. Таким образом, для смены исследуемого сечения нужно несколько изменить частоту to переменного магнитного поля B ₁.

Для задания двух других координат исследуемой области сечения организма создаются ана- логичные вспомогательные градиентные постоянные магнитные поля вдоль координат OX и OY.

Величина наведенной ЭДС в соленоиде ( 2 ), рис. 1, (т. е. МРТ-сигнал), прежде всего, пропорциональна количеству ядер того элемента, магнитный момент которых резонансно прецессирует с максимальным углом прецессии 9 на применяемой в томографе частоте переменного магнитного поля.

Это связано с тем, что гиромагнитное отношение Y зависит от вида элемента.

В настоящее время используется в основном f МГц)

водородная МРТ у = 42,67 , при которой ( Тл у получается изображение водородосодержащих тканей, прежде всего воды. Процентное содержание воды в различных тканях разное. В сером веществе мозга 83 %, в мышцах 78 %, в коже 68 % и т. д. Яркость этих тканей на МРТ-изображении будет различна. Анатомические области с малой плотностью атомов водорода, например, воздух, кости индуцируют очень слабый МРТ-сигнал и представляются на МРТ-изображении более темными. Области с большой плотностью атомов водорода более светлые. Таким образом, яркость изображения исследуемой области организма зависит от вида ткани.

Программно-компьютерными средствами обычно инвертируют, изменяют оттенки изображения, делая его более похожим на рентгенограмму (костная ткань светлая, мышечная темная).

Магниторезонансная томография, это в основном исследование морфологии тканей, но не только.

Во время паузы в подаче высокочастотного магнитного поля B ₁, катушкой ( 2 ) регистрируется МРТ-сигнал. Магнитный момент ядра , т. к. нет поступления энергии извне, начинает постепенно ориентироваться вдоль силовых линий постоянного магнитного поля – релаксировать (на рис. 1 вдоль оси Z ). Это приводит к тому, что ЭДС , наводимая в соленоиде ( 2 ), затухает. Скорость затухания (релаксации) зависит от ряда факторов.

Во-первых, от фазового состояния вещества и его плотности. В твердых телах (костях), где связь между атомами сильная, прецессирующий магнитный момент ядра во время паузы легко отдает свою энергию окружающим ядрам. Поэтому, затухание регистрируемой ЭДС будет быстрым. В жидкостях из-за более слабой связи атомов затухание происходит медленнее.

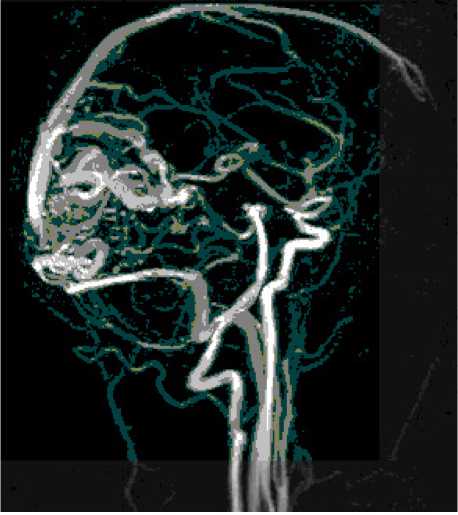
Рис. 2. МРТ-изображение кровеносных сосудов мозга и шейного отдела

Скорость затухания МРТ-сигнала определяет T скважность Q = применяемого импульсного tи переменного магнитного поля Bi (Т — период импульсного поля, tи – длительность импульса), т. к. затухание МРТ-сигнала должно успеть проявиться. Для разных тканей длительности релаксации (а, следовательно, и используемые паузы) различны и составляют от 50 мс до 2,5 с. Например, время релаксации для вещества злокачественных опухолей на 30 ^ 35 % меньше, чем у нормальных тканей за счет большей плотности опухолевой ткани, относительно окружающих тканей. Поэтому, для получения качественного МРТ-изображения определенного вида ткани нужно регулировать скважность подаваемого на ткань переменного магнитного поля B1. Все это учитывается при формировании МРТ-изображения.

Во-вторых, неподвижная жидкость (межклеточная, цитоплазма и т. д.) дает относительно сильный МРТ-сигнал. Движущаяся жидкость не дает возможности установления необходимого геометрического соответствия между направлениями внешнего постоянного магнитного поля B q , прецессирующего магнитного момента движущихся ядер и вектора индукции переменного магнитного поля B i . Ядра атомов, а, следовательно, и их магнитные моменты, в процессе движения жидкости хаотически вращаются. В связи с этим движущаяся кровь не генерирует

МРТ-сигнал. Следовательно, просветы сосудов и камеры сердца четко отграничиваются на МРТ-изображении от окружающих относительно неподвижных тканей. С этой точки зрения МРТ характеризует и функциональное состояние ткани, в частности движение крови.

Таким образом, на МРТ-изображении мы наблюдаем малоподвижные водородосодержащие ткани.

В МРТ используются следующие параметры физических величин. Индукция основного постоянного магнитного поля в пределах B q = 0,02 ^ 2 Тл. Диапазон частот переменного магнитного поля B _i определяется гиромагнитным соотношением у, т. е. видом исследуемого элемента (атома водорода). Этот диапазон частот находится в радиодиапазоне. Чувствительность МРТ позволяет различить на МРТ-изображении области размером 2–4 мм.

На рис. 2 для примера показано МРТ-изображение кровеносных сосудов мозга и шейного отдела.

Большие перспективы имеются у фосфорной

„ 31 Г        МГц )

МРТ, т. к. фосфор Р ₁3₅ у = 17,2        играет

• ⁵ С        Тл )

• 2.    Квантово-механический анализ возникновения МРТ-сигнала

важную роль в обменных процессах. Но чувстви тельность метода к фосфору составляет ~0,14 % от водородной МРТ, что связано с низкой концентрацией фосфора в организме и малым магнитным моментом его ядра (магнитные моменты протонов и нейтронов в ядре фосфора в значительной степени компенсируют друг друга). Это затрудняет использование фосфорной МРТ, т. к. из-за собственных тепловых колебаний атомов материала радиочастотной катушки (2), рис. 1, необходимо применение сверхпроводящих приемных магнитных систем, что достигается при температурах близких к абсолютному нулю по Кельвину.

Параметры прецессии магнитного момента протонов оказывают существенное влияние на величину регистрируемой ЭДС, а, следовательно, в значительной мере определяют качество визуализированной картины внутренних органов.

Рассмотрим протон с магнитным моментом (прецессирующим под углом 9 к оси Z ), находящимся в постоянном (вдоль оси Z ) B q и перпен-

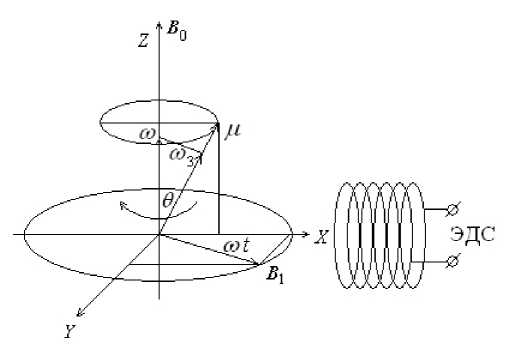
Рис. 3. Прецессия магнитного момента в постоянном и переменном магнитных полях

Также учтено:

sin 9 (с x cos to t + с у sin to t ) =

=        sin 9 cos to t +         sin 9 sin to t =

V10 J            I i 0 J

Г0

Vsin 9 ( cos to t + i sin to t )

sin 9 ( cos to t - i sin to t ) '

= Г о        e ^- i ^to t sin 9'

= Veitot sin 9        0

дикулярном ему вращающемся B 1 магнитных полях, рис. 3. На первый взгляд максимальная ЭДС (МРТ-сигнал) будет при угле прецессии 9 = 90°. В отличие от рис. 1, для удобства анализа, постоянное магнитное поле B q на рис. 3 показано вертикальным, а переменное B i горизонтальным.

Исследуем вопрос о возможности достижения такого угла прецессии (9 =90°) более подробно на основе квантово-механического подхода.

Гамильтониан системы (внешнее постоянное магнитное поле – прецессирующий магнитный момент протона) запишем в виде: ^^       ^^        ^^

H = H 0 + H int ,                                  (1)

Уравнение Шредингера для оператора взаимодействия (принято, где это не оговорено особо, Й = 1) имеет вид:

i !^ = ^H int ( t ) v, d t

где у = I I — спиновая волновая функция (спи-WJ нор) [8]; у^ — компонента спинора, если проекция магнитного момента направлена вдоль оси Z; у^ — компонента спинора, если проекция магнитного момента направлена против оси Z. Само направление вектора прецессирующего

Полагая горизонтальное переменное магнитное поле B i некоторым «возмущением», считаем H о — невозмущенной частью гамильтониана, а H int — «возмущением», связанным с воздействием поля B ₁ на невозмущенную часть системы.

Невозмущенную часть гамильтониана, используя матрицы Паули, запишем в виде [8; 9]:

магнитного момента полагаем равновесным с постоянным углом прецессии 9.

Используя представление взаимодействия [10] для гамильтониана взаимодействия, проведем преобразования:

H int ( t ) =

e

iHоt —    - iHо t _ inte

.

i

= e

ц B 0 cos 9

-ц B 0 cos 9

-

,—

- i

ц B 0 cos 9

-                  ( ц B ₀ cos 9

Hо = цbqcZ cos 9 = I о где матрицы Паули:

Г 0 1)           Г 0 - i )

Су =       , Су =         ,

X (1 0 ) ’ Y ( i 0 J ’

-ц B q cos 9

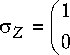
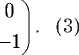
Гамильтониан взаимодействия, учитывая

B 1 ± B q , см. рис. 3, имеет вид:

H int = ц B1 sin 9 (с x cos to t + с у sin to t ) =

_ "       0         ц B1e ^- i ^{to t} sin 9^

щ B 1 e i ^{to t} sin 9         0 J ’

где to — частота переменного магнитного поля, равная частоте прецессии магнитного момента протона; t – время.

x H int e

-ц B 0 cos 9

_Г e i ц B q t cos 9

A

V

V'

e

i ц B q t cos 9

ц B 1 e

-

x

i to t

sin 9

A

ц B1e

i to t

sin 9

e

i ц B q t cos 9

x

V

e

= ц B 1 sin 9

V

e

A

, i ц B q t cos 9

. 2 i Q t

где обозначено:

Q = to

e

- 2 i Q t '

,

- ц B q cos 9 .

Таким образом, спинорное уравнение Шредингера (5) приобретает вид:

+ C -

i |V t 1= д t (V ; J	•*“ ( t > [::]=
= ц B 1 sin 9	( n      -2 г ° t A 0 e 2 2 г ° t     n ( e         0 j
= ц B 1 sin 9	e 2 г ° t v ;1 ( e 2 г ° t V f ?	.

V f . v;

Г                                   )

-° ( 1 -1 ) 2 + ц B 1 sin 9 ( 1 + 1 ) 2 1                     1

₍ ц B 1 sin 9 ( 1 - 1 ) 2 + ° ( 1 + 1 ) 2 ,

e ^{- г 6} t

Для решения уравнения (8) введем новые вспомогательные функции:

Ф t = e ° ^t V f и ф ; = e ^- i ° ^t V ; •                    (9)

В новых переменных уравнение (8) можно записать в виде:

Действительно, если для спинора в первом слагаемом (13) справедливо равенство:

Г .         1 ) Г .1 1

^{( 1 + 1)}2 „     ^{-( 1 + 1)}2 to

-          1 6 =         1

(- ( 1 -1 ) 2 J    ( ( 1 -1 ) 2 6 J

Г)

-° ( 1 +1 ) 2 - ц B 1 sin 9 ( 1 -1 ) 2

=                    11

₍ ц B 1 sin 9 ( 1 + 1 ) 2 - ° ( 1 - 1 ) 2 ,

. дф [   -° i = I дt (цB1 sin 9

ц B i sin 9) Ф, ° J ’

|V| где вспомогательный спинор ф(t) =     , или:

(ф ; J

. д f ф ) г -° i----- I I = I дt (Ф; J (цBi sin 9

ц B i sin 9 °

-°Ф t + ц B 1 sin 9ф ; ц B 1 sin 9ф t + °ф ;

то, следовательно:

Г ,                             ) Г                ,         1)

° ( 1 + 1 ) 2 - ( 1 + 1 ) 2 (6     -ц B 1 sin 9 ( 1 -1 ) 2

11 =      1

(° ( 1 -1 ) 2 + ( 1 -1 ) 2 6J  ( ц B 1 sin9 ( 1 + 1 ) 2 y

т. е.

Г.         . .        .1) Г                  .        .1)

( °-(6 )( 1 + 1 ) 2      -ц B 1 sin 9 ( 1 -1 ) 2

1                                                 1       ’ ( ( ° + 6 )( 1 -1 ) 2 J (ц B 1 sin9 ( 1 + 1 ) 2 ?

° или подставляя 1 =  , найдем:

Прямой подстановкой можно убедиться, что общее решение уравнений (10) или (11) имеет вид:

Г

(°-6)

, 1)

6 + °) 2 to J

Г

-ц B 1 sin 9

, 1) 6-°) 2 to J

ф ( t ) =

= С +

⁽1., ,- ( i -1 ) 2 ,

е^{г 6} t

+ C _

Г.          1 )

( 1 -1 ) 2

1 ( ( 1 + 1 ) 2 J

( ° + ⁶ ) (

6-°

/-V to

ц B 1 sin 9

65 + ° ^ 2

—W

(О J

J

e ^{- г 6} t

где для удобства преобразований обозначено

6 = J °² + ( ц B 1 sin 9 ) ² и 1 = —.

При подстановке (12) в (10) левая часть уравнения (10) равна:

Следовательно:

Г.          , .            1)

( °-⁶ )( ⁶ + ° ) 2

( ( °+ 6 )( 6 -° ) 2 J

Г                .         .1)

^-ц ^B 1 sin ⁹ ( ^{6 -}° ) 2

_    . 1

₍ ц B 1 sin 9 (to + ° ) 2 _?

т. е.

	Г	x 1)
i ^ = - C+ д t      +	( (-	1 + 1 ) 2    _ уд to eг 6 t + 1 ( 1 -1 ) 2 J

+ C -

- г <ь 1

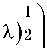
/-V

Г.          .1. ( 6 -° ) 2 ( 6 + 1	. 1) ° ) 2 1	— =	Г ( 62 I	-° 2 ) 2' 1	^-^ =
( ( ° + (6 ) 2 (( 6 - Г ц B 1 sin 9) (ц B 1 sin 9 J ’	° ) 2 J		( ( 62	-° ) 2 J

to e

-

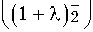
= С +

Г                                 )

-° ( 1 +1 ) 2 - ц B 1 sin 9 ( 1 -1 ) 2 1          1

₍ ц B 1 sin 9 ( 1 + 1 ) 2 - ° ( 1 - 1 ) 2 ,

e i ⁶ t

+

что справедливо т. к. й> = -^°² + ( ц B 1 sin 9 ) ².

Аналогичное доказательство можно провести и для спинора во втором слагаемом формулы (13).

При подстановке (12) в (10) правая часть уравнения (10) равна:

—Q ц B1 sin 9

ц B 1 sin 9) Ф =

Q I

= С +

—Q ц B1 sin 9

ц B 1 sin 9) ( 1 + X ) 2

Q I J

e i ^й t +

—

+ C _—

—Q ц B1 sin 9

ц B i sin 9) ( 1 — X ) 2

Q

e ^— i ^b t

—

= С +

— ц B 1 sin 9 ( 1 — X ) 2

. ц B 1 sin 9 ( 1 + X ) 2

f               1

—

1 Q ( 1 — X ) 2 ,

e i ⁶ t +

+ C _—

—Q ( 1 — X ) 2 + ц B 1 sin 9 ( 1 + X ) 2

. ц B 1 sin 9 ( 1 — X ) 2 + Q ( 1 + X ) 2 _?

e ^— i ^й t ,

что совпадает с правой частью формулы (13).

Следовательно, доказано, что функция (12) является общим решением спинорного уравнения (10).

Примем начальное условие, с учетом (9), исходя из того, что при t = 0 волновая функция ф ( 0 ) = ф ( 0 ) = 1 j. Отметим, что начальное по

времени положение вектора магнитного момента протона , прецессирующего вокруг постоянного магнитного поля В о под углом 9 носит совершенно произвольный характер.

Следовательно:

ф ( 0 ) = С +

f .         1 )

^{( 1 + X)2} 1 ₍— ( 1 — X ) 2 _?

C

f.        1)

(1■ ■

. ( 1 + X ) 2 ,

Откуда следует:

С = ( 1 — ^X ) 2

,

С

■+

= ( 1 + X ) 2

.

Подставляя (14) в формулу (12), находим частное решение уравнений (10) или (11) в виде:

ф⁽ t ) =

Ф т ) = ( 1 + X ) 2

. ф;

ei S> t +

+

e

—

i й t

f

— (

( 1 + ^X ) )

( 1 — X² ) ²

e i ^й t

^{f( 1 — X)} 1 ⁾ ₍ ( 1 — X² ) 2 ,

e ^— i ^й t =

W ( t )

( 1 — X² ) ² sin й t

,

где W ( t ) = cos й t + i X sin й t .

При этом, частное решение уравнения (5) или (8) запишется в виде:

f Vt ф( t) = I

(ф ;

^f       W ( t ) e

„—i Q t^l ФТ e iQt

(Ф ; ^e   J

,— i Q t

.

— i ( 1 — X² ) 2 e i ^Q t sin й t

Проверим условие нормировки:

pt( t) + P;( t ) = 1, где вероятности проекций магнитного протона вдоль оси Z и против оси Z, ственно равны:

^p t ( t ) = Ф т Г = W ( t ) e ^ i ^Q t Г =

= | W ( t ) 2 = cos²

P ; ⁽ t ) = ^ф ; 2 =

момента

соответ-

й t + X sin й t ,

—

■ i ( 1 — X² ) ² e i ^Q t sin b t

( 1 — X² ) ² sin й t

= ( 1 — X² ) sin² й t .

Следовательно, условие нормировки полняется.

(17) вы-

Так как существует ориентирующее магнитный момент действие постоянного магнитного поля B ₀, направленное вдоль оси Z , то естественно предположить, что угол прецессии максимальной вероятности 9 < 90°.

Заметим, что согласно (18) максимальная вероятность P t ( t ) = 1, формально, достигается при

X = — = 1, т. е. при угле 9 = 0. Однако, данный й тривиальный результат (данный максимум) физически неудовлетворителен. Магнитные моменты протонов в веществе не могут иметь одинаковый угол прецессии 9 = 0 вследствие принципа Паули. Поэтому найдем угол 9 достижения максимальной вероятности из условия:

d p _t ( t )    d p _t ( t ) db

-------=--= о .

д9

db d9

С учетом (18) и используя

1 fdQ J

— X , найдем:

to (dto      I

dX

d fQ

db d(b ( й

5 P f ( t )		= ^ t ( x 2 -1 ) sin 2t _ X 5Qj5b) tot --I — = (b 5(b J 59	- 2 sin2 to t		X 2 — +
59 + 2 sin2			_ X2 J tot — ^* (0 J		to	(21)
+ У	' t ( x 2 - 1 ) sin 2(b t - 2 sin2 V 9 • 2 - +X 5 q 2 sin tot --. to 59 читывая:			dm 59	+

— = — Jq² + ( ц B₁ sin 9 ) 2 =

59   59           1 v

= — | 2Q—+ 2 ( ц B i )² sin 9 cos 9

2o V 59

= ^ ( 2Q ( ц B _o sin 9 ) + ( ц B 1 ) ² sin 29 ) =

= 21b (®ЦBo sin 9 - ((ЦBo )2 - (ЦB1 )2) sin 29)’ найдем:

5 P^ ( t ) =

[                                2 J t (x2 - 1) sin 2(0t - 2 sin2 tot— x '                                   65

т. н. боровский радиус орбиты. Использованы константы, приведенные в [11]. Предполагая, что скорость перехода электрона на более высокую орбиту равна скорости электрона на орбите, оценим время перехода по формуле r mr2           -16

т ~   =     ® o, 24 ■ 1o с. Полученная величи-

V   Й на намного меньше даже времени нахождения электрона на возбужденной орбите ~ Ю-8 с.

Кроме того, в формуле (22) время является непрерывной величиной, оно не квантуется. Однако, угловая скорость to и угол прецессии 9 квантуются. Квантование 9 определяется тем, что проекция магнитного момента протона на направление постоянного магнитного поля B ₀ может принимать только дискретный ряд значений. Поэтому и угол прецессии 9 также имеет дискретный, квантовый характер. Вследствие

5 P (t)

этого, нахождение производной       по кван-

59

туемой величине носит приближенный характер и возможно только при большой дробности угла

x 21b (оЦBo sin 9 - ((ЦBo )2 - (ЦB1 )2) sin 29) +

+ 2 sin² (b t — ц B o sin 9 = 0

«

прецессии, что справедливо при относительно больших величинах 9.

или

to    (цBo ) - (цB1)

---

2 V      ц Bo      J

Вследствие вышесказанного, приближенное равенство (22) должно иметь разный вид для различных отрезков времени o <  t < т — переходного процесса и t > т — равновесной прецес-

сии:

X sin (b t

^X 2       2

sin to t--t ( X² - 1 ) cos to t

«

b

^^^^^^^^^^   ^^^^^^в

' ( ц B o ) ² - ( ц B 1 ) 2 ' ц Bo

o < t <т cos 9 ~

.

o < t <т

X sin to t

Для корректности дальнейших преобразований необходимы некоторые физические предпосылки. Формула (22) отражает фактически два процесса: процесс перехода магнитного момента к равновесной прецессии и сам процесс равновесной прецессии.

Установление равновесного угла прецессии – это квантовый переход протона из одного состояния в другое.

Время перехода квантовой системы из одного состояния в другое очень маленькое, значительно меньше времени нахождения системы в каком либо состоянии. Например, согласно теории Бора скорость электрона на орбите атома водо

Й      Й         -4 Дж рода V =---, где — = 1,16 ■ io         — приве- mr m           Гц ■ кг денный квант циркуляции, r = o, 53 ■ 1o 1o м —

X2

— sin to t - t ( X² -1 ) cos to t

(b                   V '

t >^т Хо

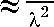
q

X2 .

Преобразовывая (23), найдем:

[(цBo )2-(ц B1)2 J cos 9 =

V      ц Bo      J л    (ц B1 sin 9)2

= цB, cos 9 -    ------—,

ob цBo cos 9

или

to cos 9

2ц B o

- cos2 9 I = sin2 9 .

Откуда следует:

cos q = 2ц Bo = °r cos                   ,

где to _r = 2ц B o — резонансная частота прецессии.

Формула (24) фактически совпадает со своим классическим аналогом для прецессии сфериче-ски-симметричного тела (волчка) [12]. Действительно, угловая скорость вращения тела вокруг M своей оси tog = — cos 9, где М — механический I3

момент, действующий на волчок, I3 – момент инерции вокруг собственной оси вращения волчка. Учитывая, что частота прецессии волчка M to = —, где I} - момент инерции волчка вокруг I1

оси, перпендикулярной собственной оси враще-Is to ния волчка, находим cos 9 = — ——. Для сфериче-I1 to ски-симметричного волчка Ii = 13, следовательно:

cos 9 = to ,                                    (25)

где к> з — угловая скорость вращения тела вокруг своей оси, аналог резонансной частоты прецессии. Индексы величин использованы по аналогии с [12]. Заметим, что вектор ₃ совпадает по направлению с прецессирующим магнитным моментом , см. рис. 3.

• 3.    Оценки параметров магниторезонансной томографии

Максимальный МРТ-сигнал (ЭДС) возникает в регистрирующей катушке при угле прецессии магнитного момента 9 = 90°. В соответствии с формулой (24) угол прецессии 9 ^ 90° в случае увеличения частоты to внешнего переменного магнитного поля B i до бесконечности или уменьшении внешнего постоянного магнитного поля B q до нуля. Последнее обстоятельство связано с уменьшением ориентирующего действия постоянного магнитного поля на магнитный момент .

Однако, использование слабых постоянных магнитных полей невозможно, т. к. необходимо преодолеть хаотическое направление магнитных моментов протонов, которое появляется в результате теплового воздействия тканей организма. С этой точки зрения возникает противоречивая ситуация, когда с одной стороны постоянное магнитное поле Bq должно быть достаточно сильным, чтобы магнитные моменты протонов в водородосодержащих тканях организма в исследуемой области были в основном направлены вдоль этого поля. С другой стороны величина постоянного магнитного не должна сильно препятствовать возникновению достаточно большо- го угла прецессии магнитного момента протонов в соответствии с формулой (24).

Оценим частоту переменного магнитного поля

2Ц Bq по формуле to =----. Предположим, что опти- cos 9

мальный угол прецессии 9 = 45°. Величину внешнего постоянного магнитного поля найдем из примерного равенства энергий ориентирующего магнитный момент действия постоянного маг- нитного поля и хаотизирующего действия теп- ла организма

^Ц 0 ^в 2 =

a N A kT или B q =

1 2a N A kT Ц о

В последней формуле T ® 300° K — температура -23 Дж тела организма, к = 1,38 ■ 10       — постоянная

23     1

Больцмана, NA = 6,02 ■ 10        — число Аво- моль л п-7 Гн гадро, Цо = 4п ■ 10      — магнитная постоянная,

м a ~ 10-10 моль — доля моля протонов (~ 10-10 г) водородосодержащих тканей в области визуализации, которые подвергаются воздействию переменного магнитного поля. Следователь- но, индукция постоянного магнитного поля Bq ® 0,63 Тл. Таким образом, частота переменного магнитного поля равна to = ^Ц^0 ® 2, 4 ■ 108 c-1 cos 9

или V ® 38 МГц, т. е. лежит в области ультравы-соких частот (в радиодиапазоне).

Заключение

При расчете параметров постоянного и переменного магнитных полей в магнито-резонансном томографе следует учитывать необходимость поиска оптимума применяемых параметров. Это нужно вследствие того, что существует разнонаправленность действия этих полей на магнитные моменты прецессирующих ядер (протонов) атомов водорода. Постоянное магнитное поле уменьшает угол прецессии, что ведет к уменьшению МРТ-сигнала. Одновременно, постоянное магнитное поле создает ориентирующее действие на магнитные моменты, препятствующее хаотическому действию теплового движения. Увеличение частоты переменного магнитного поля приводит к увеличению угла прецессии, что ведет к увеличению МРТ-сигнала.

При расчете прецессии магнитного момента в постоянном и переменном магнитных полях можно использовать классические формулы, следующие из теории регулярной механической прецессии твердого тела (волчка).