Оптимизация параметров модели выпуска продукции с учетом вредных выбросов

Многие математические модели естественнонаучных и социальных процессов приводят к постановкам задач оптимального управления и оптимизации управляющих параметров. Поэтому разработка эффективных методов, технологий и алгоритмов, необходимых для численного решения сложных практических задач, не теряет своей значимости и актуаль- ности. Применяемый в работе метод неподвижных точек может служить хорошим инструментом для решения таких задач, в частности, для задач параметрической оптимизации. Описание метода и его свойств дано в работах [4, 5]. Метод неподвижных точек обладает рядом существенных преимуществ, например, возможностью строго улучшения управлений, удовлетворяющих дифференциальному принципу максимума, что подтверждают численные расчеты на тестовых примерах [8, 9]. В статье метод применяется для оптимизации параметров модели выпуска продукции с учетом отрицательного влияния загрязнения. Она исследуется в работах [7, 10]. Ставится задача получить оптимальные расчетные значения модели указанным методом и сравнить полученные и известные результаты.

1.    Метод решения

Рассматривается задача оптимизации управляющих параметров в следующей постановке

Ф ( и ) = ф (x ( t j )) + [ F ( x ( t ), и , t ) dt ^ min, T                       u ∈ U

x(t) = f (x(t),и,t), x(to) = x0, tе T = [10,tj, в которой x(t) = (xj(t),...,xn(t)) - вектор состояния, и = (и,,...,um) - вектор управляющих параметров со значениями в выпуклом множестве U с Rm. Начальное состояние x0 и промежуток управления T заданы.

Предполагаются выполненными следующие условия:

• 1)    функция ф ( x ) непрерывно-дифференцируема на Rⁿ , вектор-функция F ( x , и , t ), векторная функция f ( x , и , t ) и их производные F_x ( x , и , t ), F_u ( x , и , t ), f_x ( x , и , t ), f_u ( x , и , t ) непрерывны по совокупности аргументов ( x , и , t ) на множестве R n х U х T ;

• 2)    функция f ( x , и , t ) удовлетворяет условию Липшица по x в R n х U х T с константой L > 0

II f ^{( x} , ^и , t ) ^- f ⁽ у , ^и , t )|| <  L ||x ^- у || .

Строится релаксационная (улучшающаяся) последовательность управлений, определяемых на каждой итерации в ходе решения задач улучшения, формулируемых в следующей форме: для заданного управления и е U требуется найти управление v е U с условием Ф ( v ) <Ф ( и ).

Для реализации задачи улучшения предлагается решить задачу о неподвижной точке (ЗНТ) [4, 5]:

v = PU (и + a(j^Ни (p(t,и,v),x(t,v), и, t)dt + s)), и е U, v е U, s е Rm, (3) где PU - оператор проектирования на множество U в евклидовой норме, a > 0 - параметр проектирования, H(p, x, и, t) - функция Понтрягина, x(t, v) - решение системы (2) при и = v, p(t, и, v) - решение дифференциально-алгебраической сопряженной системы вида p (t) = - Hx (p (t), x (t, u), u, t) - r (t), (Hx (p (t), x (t, u), u, t) + r (t), x (t, v) - x (t, u)} = = H (p (t), x (t, v), u, t) - H (p (t), x (t, u), u, t)

с краевыми условиями

p ⁽ t i ) = ^-Ф х ^{( x (} t i , ^u )) ^- q ,

(Фх ( x ( t i , u )) + q , x ( t i , v ) - x ( t i , u )} = ф (x ( t 1 , v )) - ф ( x ( t i , u )).

Величина s определяется соотношением

L ( H ( p ( t , u , v ), x ( t , v ), v , t ) - H ( p ( t , u , v ), x ( t , v ), u , t ) ) dt =

T                                                    \                  (4)

= \J T H ( p ( t , u , v ), x ( t , v ), u , t ) dt + s , v - u^ .

Для решения задачи о неподвижной точке (3) используется итерационный алгоритм при k >  0 :

v k ^{+ i} = P u ( u + a (\_TH_U ( p ( t , u , v^k ), x ( t , v^k ), u , t ) dt + s^k )), v ⁰ e U ,     (5)

в котором величина s^k удовлетворяет соотношению (4) при v = v^k .

• 2.    Модель выпуска продукции с учетом вредных выбросов

Рассмотрим модель выпуска продукции с учетом вредных выбросов, исследуемую в [7, i0]:

dK

— = (i - a - в ) F ( K ) - p K , dt

dP

— = (i - dp)F(K) - bP, dt где K(t) - капитал; P(t) - объем загрязнения; F(K) = i0K0.5 - объем выпуска; a > 0; p > 0 - доли выпуска на потребление и борьбу с загрязнением соответственно; p - доля выбытия капитала; d - удельное загрязнение (ед. продукции); b - скорость очистки; r - ставка дисконтирова- ния.

Ставится задача максимизации полезности (общего благосостояния) от выпускаемой продукции с учетом отрицательного влияния загрязнения:

I (a, в) = Je -rt [(aF (K ))0.5 - P1J / 5000] dt ^ max.(7)

Ограничения на управляющие параметры следующие:

a > 0, в > 0, a + в < i.(8)

Для ее численного решения приведем систему к виду, не содержащему интегралов:

K & = (i - a - в )i0 K⁰⁵ - p K ,

L = e - ^rt ( ( i0 a ) ^0.5 K ⁰²⁵ - P ^1J / 5000 ) .

Функционал примет вид

I ( а , в ) = - L ( T ) ^ min.                    (10)

Значения числовых параметров равны: ц = 0.06; Ь = 0.1; а = 10; r = 0.05.

В статье [10] проведено аналитическое исследование и получены две пары приближенно-оптимальных решений данной задачи:

а * = 0.68462, в ₂ = 0.06992; а * = 0.7264, в₂ = 0.0 .

Начальные условия для переменных состояния в [10] не задавались.

В данной работе при проведении численных расчетов задачи в качестве начального состояния выбиралось стационарное решение системы до воздействия на нее управлением. Для этого приравняем нулю управление ( а = 0, в = 0) и решим систему уравнений:

10 К ^0.5 - ц К = 0,

10 К ^0.5 - ЬР = 0.

Решив систему относительно К , P , получаем следующие выражения: К * = 100/ ц ² ; P * = 100/( Ь ц ) .

Далее модель приводилась к безразмерному виду заменой перемен- ных:

у , = К / К * ; у ₂ = P / P * ; у 3 = L .

Отсюда, К = У ] • К * ; P = у ₂ • P * ; L = у 3 .

Система примет вид:

_ К  (1 - а - в )10 К °-⁵ - цК ^{(1 - а - в )10} у ^ ( ^К * Г ^- Ц У 1 ^К *

= Кё =       К "         К"

(1 - а - в )10 у 0.5 ( К * )" ⁵

-

(1 - а - в )10 у ^^{5 ц} y 1       /         э\0.5

( 100/ ц ² )

-

цУ1 = (1 - а - в) цу"

^- ц у 1 ,

Р (1 - а в )10 к °-⁵ - bP  (1 - а в )10 у^ к * ) ⁰⁵ - Ьу ₂ p *

^у 2 ⁼ У ⁼------ Р * ------ ⁼--------- Р *---------

(1 - а в )10 у 0.⁵ ( к * ) ^0.5 _        (1 - а в )10 у 0.⁵ (100/ ц ² ) ⁰⁵

Р *             ^{у 2} =         100/( Ь ц )

= e - rt ( ( 10 а ) ^0.5 у^К *) ⁰-²⁵ - у 2^.1 • ( Р * )^{V 1} /5000 ) =

= e - rt ( ( 10 а ) ^0.5 у 0^.25 (100/ ц ² f²⁵ - у 2^.1 • (100/ Ь ц ) ^1.1 / 5000 ) =

= e - rt ( 10 а ^0.5 у⁰'⁵ / ц ⁰⁵ - у^ • ( 100 / ( Ь ц ) )^и /5000 ) .

В итоге получим:

у₃ = e - rt ( 10 ц ^{- 0.5} а ^0.5 у 0^.25 - ( 100/ ( Ь ц ) ) 1^.1 ( 1 / 5000 ) - у 21 ) , у 3 (0) = 0

Для удобства перейдем в задаче к стандартным переменным x и u (обозначим у за x , а и в за и 1 и и 2 ):

x = (1 - и 1 - и 2 ) ц л - Ц X ₁,                         Х 1 (0) = 1,

Х 2 = (1 - du 2 ) bx 0^.5 - bx 2 ,                               x 2 (0) = 1,              (11)

x₃ = e - rt ( 10 ц - ⁰⁵ u 0^.5 x 0^.25 - ( 100/( Ь ц ) ) 1^.1 - ( 1/5000 ) • x 2^.1 ) , x 3 (0) = 0,

F ( u 1 , и 2 ) = - x 3 ( T ) ^ min.

Численные расчеты проводились с приведенной системой (11).

3.    Численные эксперименты

В источниках [7, 10] не указано значение времени T . Поэтому расчетное значение T подбиралось таким образом, чтобы функционал благосостояния F ( u 1 , и 2 ) = - J e - rt ( 10 ц ^{- 0.5} u 0^.5 x 0^.25 - ( 100/( Ь ц ) ) 1^.1 - ( 1/5000 ) - x 2^.1 ) dt 0

практически не менялся при дальнейшем увеличении T (изменение не превышало 1%). Результаты представлены в таблице 1. Экспериментально было определено значение T , приближенно равное 80 единицам. Таким образом, оптимизация параметров модели проводилась на отрезке [0,80].

Таблица 1. Значения функционала благосостояния

T	Значение функционала приведенной модели ( F )	Fk + 1 - Fk Fk
1	-21,4872
5	-112,7012	4,2450389069
10	-201,9331	0,7917564321
15	-270,8653	0,3413615697
20	-323,421	0,1940289140
25	-363,2181	0,1230504513
30	-393,2582	0,0827054048
40	-432,9987	0,1010544726
50	-455,6659	0,0523493489
60	-468,6847	0,0285709332

70	-476,224	0,0160860809
80	-480,6262	0,0092439692
90	-483,2158	0,0053879709
100	-484,7491	0,0031731164

Также был проведен численный анализ рассматриваемой задачи на выполнение свойства неотрицательности переменных состояния x ₁( t ), x ₂( t ). По физическому смыслу они должны быть неотрицательными, так как обозначают объем капитала и загрязнения, соответственно. Анализ выполнялся путем численных расчетов задачи Коши для безразмерной модели при различных значениях параметров u ₁, u ₂. В ходе численных расчетов было получено, что для и 2 >  0.1 при любых допустимых значениях u ₁ переменная x ₂ ( t ) на рассматриваемом интервале с некоторого момента принимает отрицательные значения. Поэтому допустимое множество было ограничено следующими условиями:

и 1 >  0, и ₂ >  0, и ₂ <  0.1, и₁ + и ₂ <  1 .

Отдельно решалась задача проектирования на указанное множество, при этом рассматривалось 9 областей, в которые может попасть проектируемая точка. Для каждой из этих областей легко определяется проекция точки (Рис. 1).

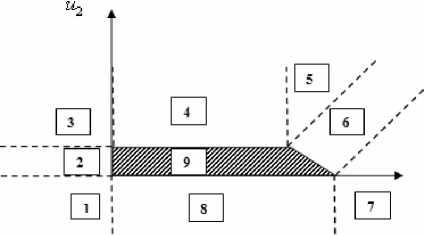
Рис. 1. Области проектирования на допустимое множество управлений Функция Понтрягина и ее частные производные по состоянию и управлению имеют следующий вид:

H = p 1 • ( (1 - и 1 - и ₂) ^x®⁵ - цx₁ ) + p ₂ ( (1 - du ₂) bx^ - bx ₂ ) + + p 3 e - rt ( 10 ц "0.5 и ^⁵ x ^ ²⁵ - ( 100/ ( Ь ц ))^М ^ ( 1/5000 ) x 2 ^.1 ) , H x = 0.5 ц (1 - и 1 - и ₂) p 1 Х 1-0.5 - ц р 1 + 0.5 b (1 - du ₂) p ₂ x -^⁵ + + 2.5 ц ^{- 0.5} e ^{- rt}u ₁ ⁰ . ⁵ p 3 • x f⁰⁵⁵ ,

H_x =- bp ₂ - ( 100/ ( Ь ц ) ) ^1.1 ^ ( 1.1/5000 ) e ^{- rt}p ₃ x ₂ ^0.1 ,

H = 0, x3

H =- ц Р 1 x 0" + 5 ц ^{- 0.5} e ^{- р} p 3 x ^²⁵,

H u 2 =-ц P 1 x' 5 - bdp 2 x' 5 .

Задача о неподвижной точке (3) принимает вид:

v = P ( ^U 1 + a ⁽ J T H ⁽ p ⁽ t , ^u , v ), x ⁽ t , v ), ^u , t ) dt + ^ 1 ),

^U 2 ⁺ a ⁽ \ T ^H u ₂ ⁽ P ⁽ t , ^U , v ), x ⁽ t , v ), ^U , t ) ^{dt + 5} 2 ⁾⁾,                    ⁽¹²⁾

u = ( u₁, u ₂ ) G U , v = ( V 1 , v ₂ ) G U , 5 = ( 5 1 , 5 ₂ ) G R ² .

Дифференциально-алгебраическая сопряженная система: p 1 ( t ) = - 0.5 ц (1 - u 1 - u ₂) p₁ x - ^0.5 + ц p₁ - 0.5 b (1 - du ₂) p ₂ x - ^0.5 -- 2.5 ц ^{- 0.5} e ^{- rt}u 0^.5 p ₃ • x ^{- 0}.⁷⁵ - r 1 ( t ),

I ¹⁰⁰ | 1.1      - rt     01

p 2 ⁽ t ) = bp 2 ⁺ h— | 7777- e p 3 ^{x 0} - ^r 2 ⁽ t ), ^ Ь ц ) 5000 ^p 3 ⁽ t ) = ^{- r} 3⁽ t ),

( H x ( p ( t ), x ( t , u ), u , t ) + r ( t ) ) ( X 1 ( t , v ) - X 1 ( t , u ) ) +

+ ( H x ₂ ( p ( t ), x ( t , u ), u , t ) + Г 2 ( t ) ) ( x 2 ( t , v ) - x 2 ( t , u ) ) +

+ ( H x 3 ( p ( t ), x ( t , u ), u , t ) + r , ( t ) ) ( x 3 ( t , v ) - x з ( t , u ) ) =

= H (p (t), x (t, v), u, t) - H (p (t), x (t, u), u, t), p1( T) = 0, p 2( T) = 0, p з( T) = 1.

Программная реализация численного алгоритма осуществлялась на языке программирования Fortran PowerStation 4.0 (FPS). Численный итерационный алгоритм (5) для решения задачи о неподвижной точке (12) проводился до первого строгого улучшения управления u g U . Далее строилась новая задача о неподвижной точке и итерационный алгоритм расчета повторялся. В качестве критерия остановки решения последовательных задач улучшения управления выбиралось условие ||vk ^{+ 1} - v^k ||< s || v^k || в евклидовой норме, где е >  0 - заданная точность, vk -релаксационная последовательность генерируемых управлений. Блок-схема алгоритма представлена на рисунке 2. Численное интегрирование задач Коши для дифференциальных систем уравнений реализовывалось методом Рунге-Кутта-Вернера переменного (5-6) порядка и шага с помощью программы DIVPRK библиотеки IMSL FPS.

В качестве заданной точности расчетов выбиралось значение s = 10 ^{- 5} . Расчеты проводились для различных начальных значений параметров, в том числе, для приближенно-оптимальных значений, полученных в статье [10]. Расчеты проводились при различных значениях параметра a , ука-53

занных в таблице. В итоге рассматриваемым методом неподвижных точек были получены расчетно-оптимальные значения параметров задачи V = 0.9, v₂ = 0.1, которым соответствует значение функционала F = F ( v , , v ₂) = - 537,48. Отметим, что полученным в работе [10] оптимальным параметрам соответствуют следующие значения функционала на рассматриваемом интервале наблюдения:

F ( а , * , р ; ) = - 480,78, а , * = 0.68462, в ₂ * = 0.06992, F ( а ₂ * , в ₂ * ) = - 440,37, а * = 0.7264, в ₂ * = 0.0 .

Результаты расчетов представлены в таблице 2.

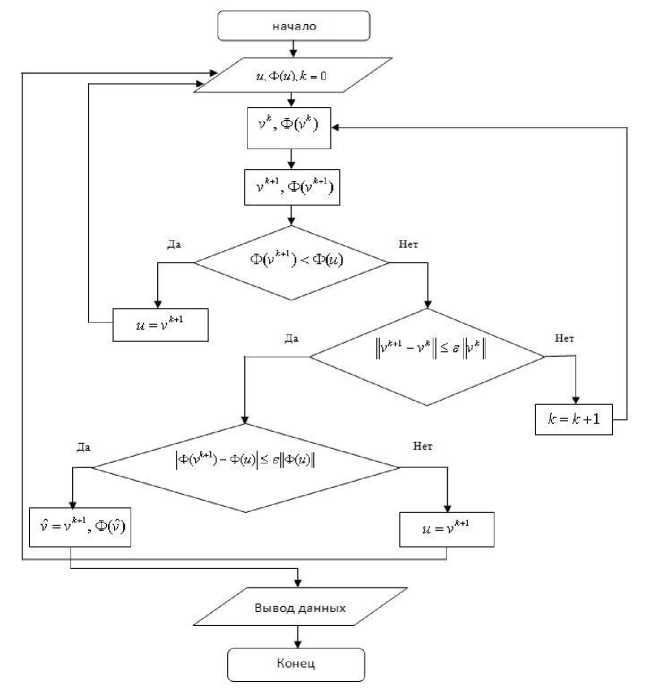
Рис. 2. Блок-схема алгоритма метода неподвижных точек

Таблица 2. Результаты расчетов параметров модели

a	u	v 0	v	F ( v )	Число ЗНТ
1	0.01 0.01	0.01 0.01	0.900 0.100	-537.48	3
	0.1 0.1	0.1 0.1	0.900 0.100	-537.48	3
	0.3 0.01	0.3 0.01	0.900 0.100	-537.48	2
	0.6 0.01	0.6 0.01	0.900 0.100	-537.48	2
	0.9 0.01	0.9 0.01	0.900 0.100	-537.48	2
	0.685 0.07	0.685 0.07	0.900 0.100	-537.48	2
	0.726 0.0	0.726 0.0	0.900 0.100	-537.48	2
10 - 6	0.685 0.07	0.685 0.07	0.900 0.100	-537.48	682
10 - 3	0.685 0.07	0.685 0.07	0.900 0.100	-537.48	2
10 3	0.685 0.07	0.685 0.07	0.900 0.100	-537.48	2
10 6	0.685 0.07	0.685 0.07	0.900 0.100	-537.48	2

Заключение

Рассматриваемый в работе метод неподвижных точек разработан для оптимизации параметров нелинейных динамических систем. Метод характеризуется отсутствием трудоемкой операции выпуклого или игольчатого варьирования, характерной для градиентных методов. Сходимость метода регулируется выбором одного проекционного параметра a >  0, что значительно упрощает настройку метода для решения конкретных прикладных задач. Указанные свойства метода являются существенными факторами повышения эффективности решения задач параметрической оптимизации. Проведенные численные расчеты и полученные результаты подтверждают достаточно высокую эффективность предлагаемого метода в рамках рассматриваемой модельной задачи.