Оптимизация распределения времени на изучение модулей цикла усовершенствования организаторов здравоохранения

¹ Введение. Подготовка высококвалифицированных организаторов здравоохранения — одна из важных задач, стоящих перед медицинскими государственными образовательными учреждениями высшего профессионального образования, которые при этом опираются на требования государственных образовательных стандартов. Так, приказом Минобрнауки России от 26.08.2014 № 1114 «Об утверждении федерального государственного образовательного стандарта высшего образования по специальности 31.08.71 Организация здравоохранения и общественное здоровье (уровень подготовки кадров высшей квалификации)» (зарегистрирован в Минюсте России 25.09.2014 № 34131) определены профессиональные задачи, которые должны быть готовы решать лица, освоившие программу соответствующего обучения. Кроме того, для организаторов здравоохранения установлены универсальные и профессиональные компетенции, а также общие требования к структуре программы профессиональной подготовки. Вместе с тем указывается, что при разработке программы обучения требования к отдельным её модулям и практикам организация устанавливает самостоятельно, что вызывает определённые трудности у профессорско-преподавательского состава, формирующего соответствующие учебно-методические комплексы. При этом могут решаться следующие задачи:

прямая — распределить время, отводимое на отдельные модули, чтобы сумма баллов, получаемых организаторами здравоохранения, была максимальной для конкретного бюджета времени и по каждому модулю оценка была не ниже, чем «удовлетворительно»;

обратная — для различных значений среднего балла изучения цикла усовершенствования получить минимальные значения времени на его прохождение.

Цель : рациональное (оптимальное) распределение времени на изучение модулей аттестационного (сертификационного) цикла усовершенствования организаторов здравоохранения.

Материал и методы . Проведён экспертный опрос 73 руководителей здравоохранения медицинских организаций Саратовской области, проходивших усовершенствование на факультете повышения квалификации и профессиональной переподготовки специалистов Саратовского государственного медицинского университета им. В. И. Разумовского (СГМУ) по специальности «Организация здравоохранения и общественное здоровье». При отборе экспертов были использованы следующие критерии: опыт профессиональной деятельности по специальности не менее 5 лет и компетентность. Применялся метод самооценки с определением совокупного индекса — коэффициента компетентности — среднее значение уровня теоретических знаний, практических навыков и способности к прогнозированию (не менее 4 баллов по 5-балльной шкале) [1].

Для реструктуризации учебной программы усовершенствования организаторов здравоохранения использован метод ветвей и границ (МВГ) [2–4].

Результаты. На основе экспертного опроса получены сведения о том, сколько часов занятий необходимо для изучения каждого из семи модулей цикла

усовершенствования организаторов здравоохранения в СГМУ на оценки «удовлетворительно», «хорошо», «отлично» (табл. 1).

Таблица 1

Распределение времени на изучение модулей цикла усовершенствования организаторов здравоохранения в зависимости от его успешности (часы)

Модули	Оценка
	Удовлетворительно	Хорошо	Отлично
1. Организация здравоохранения и общественное здоровье, методы изучения и оценки	15	24	41
2. Система охраны здоровья населения	15	21	30
3. Экономика здравоохранения в условиях реформы	26	47	66
4. Управление качеством медицинской помощи	21	35	46
5. Правовые основы здравоохранения на современном этапе	23	34	45
6. Организационнометодическая работа в учреждениях здравоохранения. Медицинская статистика	21	27	39
7. Менеджмент и маркетинг в здравоохранении	24	46	65
Итого:	145	234	332

Из табл. 1 видно, что минимальный бюджет времени, который может быть выделен на изучение рассматриваемых модулей, составляет 145 часов, а максимальный, позволяющий получить по всем дисциплинам оценку «отлично», — 332 часа. Последующие действия осуществлялись для значений констант ограничений из данного интервала времени.

Рассмотрим математическую постановку задачи. С этой целью введем обозначения:

d_j ( x_j ) — время, необходимое для изучения j -ого модуля с целью получения оценки «удовлетворитель но » ( x_j =1), «хорошо» ( x_j =2), «отлично» ( x_j =3), j = 1, n ,где n —числомодулейанализируемогоцикла;

x_j — номера возможных значений времени d_j ( x_j ), x, d j ( X j ) , X j e { 1,2,3 } ;

C_j ( x_j ) — значения оценок (в баллах) по j -модулю, в частности, C_j ( x _j =1 )=3; C_j ( x_j =2)=4; C_j ( x_j =3)=5 C j ( X j = 3 ) = 5 V j = i n ;

n — число модулей анализируемого цикла;

D ⁰ — время, выделяемое на изучение модулей данного цикла (константа ограничений).

С учетом введенных обозначений прямая задача заключается в следующем:

Найти вектор X = { x_j , j = 1, n } , доставляющий максимальное значение функции

n

C = max ^ C j ⁽ x j ) x j j = 1 при выполнении ограничения

n

Z d j ( X j ) ^ D 0

j = 1

Не менее важной является обратная, по отношению к (1), (2), задача. Допустим, на основе эксперт- ного опроса получены сведения о том, сколько часов занятий необходимо для изучения отдельных модулей на оценки «удовлетворительно», «хорошо», «отлично». Пусть определен суммарный балл изучения рассматриваемого цикла дисциплин.

Необходимо так распределить время, отводимое на изучение отдельных модулей, чтобы продолжительность всего цикла была минимальной при условии, что суммарный балл — не меньше заданного значения и по каждому модулю оценка не ниже, чем «удовлетворительно».

Математическая постановка задачи заключается в следующем.

Найти вектор X = { x j , j = 1, n } , доставляющий минимальное значение функции

n

D = min £ j _Xj] ^Xj j = i

при выполнении ограничения

n

Z C j ( X j ) ^ C 0 ,                 (4)

j = 1

где C⁰ — заданный суммарный балл изучения цикла.

Задачи (1), (2) и (3), (4) относятся к области целочисленного программирования. Для их решения используем метод ветвей и границ (МВГ) [2–4].

Не снижая общности, решение рассмотрим для задачи (3), (4). Общая идея метода заключается в замене полного перебора перебором частичным на основе построения нижних оценок и исключения бесперспективных вариантов.

С этой целью для каждого элемента x j ( j = 1, n ) вычисляют нижние оценки, исходя из следующего рассуждения: какое, в лучшем случае, будет значение целевой функции, если в решение войдет рассматриваемый элемент.

Далее из всех элементов в решение включают такой элемент r_j , который имеет наименьшую оценку T_j ( r_j ), и из него проводят дальнейшее ветвление. Вновь вычисляют оценки уже для элементов ( j +1) — го уровня ветвления и т.д.

На последнем уровне ветвления имеем решение (пока, возможно, приближенное), т.е. набор элементов, вошедших в систему, обеспечивающих заданное значение времени, отводимого на изучение всех модулей, и значение целевой функции T ⁰ ( r_n ). Далее проверяем решение на оптимальность и, если возможно, уточняем его.

Проверка на оптимальность заключается в следующем.

Поднимаемся на ( n -1) — й уровень ветвления. Смотрим, есть ли вершины (концевые, неветвлен-ные) с оценками, лучшими, чем значение T ⁰ ( r_n ). Если есть — проводим уточнение путем ветвления из вершины с наилучшей оценкой.

В противном случае поднимаемся на уровень ( n –2) и т.д. Если все уровни будут просмотрены, то решение заканчиваем.

В соответствии с МВГ первоначально рассчитывается нижняя граница целевой функции T ^*. Если на n -м уровне ветвления значения T ⁰ ( r_n ) и T ^* совпадают, то решение заканчиваем.

Таким образом, из качественного описания МВГ следует, что здесь существенными являются три момента [2]:

• а)    вычисление оценки границы решения для каждого элемента вершины;

• б)    определение правила ветвлений;

• в)    отсечение бесперспективных вершин.

Для задачи (1), (2) на уровнях ветвления отыскивают не нижнюю, а верхнюю границу со всеми вытекающими вычислительными особенностями.

Более подробно методы решения задач (1), (2) и (3), (4) изложены, например, в [2, 3].

Исходные данные, представленные в табл. 1, были использованы для решения задачи распределения учебного времени по семи модулям цикла. Результаты решения задачи для различных значений ограничений на допустимое время, отводимое на изучение цикла, приведены в табл. 2.

Таблица 2

Обобщенные результаты решения прямой задачи

Ограничение на время ( D 0 ), час	Оптимальное суммарное значение среднего балла / оптимальное значение среднего балла/ реальное время, необходимое для изучения цикла	Оценки по модулям*
145	21/3,0/145	3,3,3,3,3,3,3
150	21/3,0/145	3,3,3,3,3,3,3
175	25/3,57/175	4,5,3,3,3,4,3
200	27/3,86/197	4,5,3,3,5,4,3
225	29/4,14/222	5,4,3,5,5,4,3
250	30/4,29/239	5,5,3,5,5,4,3
275	32/4,57/273	5,5,3,5,5,5,4
300	33/4,71/291	5,5,5,5,5,5,3
325	34/4,86/313	5,5,5,5,5,5,4
332	35/5,0/332	5,5,5,5,5,5,5

П р и м еч а н и е : *– последовательность оценок соответствует представлению модулей в табл. 1.

Таким образом, полученные результаты решения данной прямой задачи позволили обоснованно определить время, необходимое для изучения модулей внутри рассматриваемого цикла.

Рассмотрим решение обратной задачи. Для различных значений суммарного балла изучения цикла с использованием МВГ получены минимальные значения времени на изучение цикла (табл. 3).

Таблица 3

Обобщенные результаты решения обратной задачи

Ограничение на суммарный балл, C 0	Средний балл	Минимальное время, необходимое для изучения цикла, час / реальное значение суммарного среднего балла	Оценки по модулям*
21,0	3,0	145/21	3,3,3,3,3,3,3
22,4	3,2	157/23	3,4,3,3,3,3,3
23,8	3,4	166/24	3,5,3,3,3,4,3
25,2	3,6	186/26	4,5,3,3,4,4,3
26,6	3,8	197/27	4,5,3,3,5,4,3
28,0	4,0	209/28	4,5,3,3.5,5,3
29,4	4,2	234/30	4,5,3,5,5,5,3
30,8	4,4	251/31	5,5,3,5,5,5,3
32,2	4,6	291/33	5,5,5,5,5,5,3
33,6	4,8	313/34	5,5,5,5,5,5,4
35,0	5,0	332/35	5,5,5,5,5,5,5

П р и м еч а н и е : *– последовательность оценок соответствует представлению модулей в табл. 1.

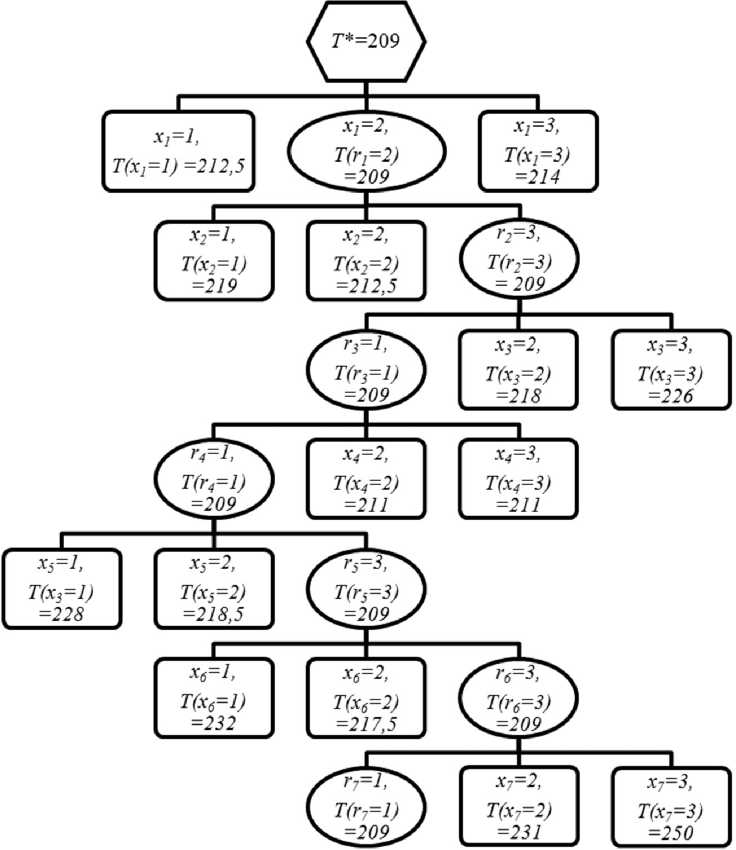
Рис. 1. Граф-дерево ветвлений для значения С0, равного 28

Ход решения задачи в соответствии с МВГ для ограничения C ⁰=28 приведен на рис. 1. Вн утр и фигур записаны значения переменных x, j = 1,7 и соответствующие нижние оценки T_j ( x_j ). В овалах показаны вершины, из которых следует проводить дальнейшее ветвление. В данном примере оценки T ⁰ ( r ₇) и T ^* совпадают.

Анализ результатов решения позволяет сделать обоснованный выбор времени, необходимого для изучения модулей внутри рассматриваемого цикла, для различных значений среднего балла.

Обсуждение. В современных условиях развития здравоохранения система подготовки специалистов и практика управления персоналом медицинских организаций ориентированы на формирование компетентных, конкурентоспособных врачебных кадров, в частности руководящего состава [5, 6]. Такая подготовка осуществляется в рамках аттестационных (сертификационных) циклов усовершенствования и должна соответствовать требованиям государственных образовательных стандартов. При этом актуальным является рациональное (оптимальное) распределение времени на изучение всего цикла обучения и каждого модуля (дисциплины). В настоящем исследовании эти задачи были решены с использованием

МВГ. Аналогично можно обосновать распределение времени на изучение тем внутри модуля (дисциплины).

Заключение. Рассмотрена важная в прикладном плане задача оптимального распределения времени на изучение модулей аттестационного (сертификационного) цикла усовершенствования организаторов здравоохранения. Предлагаемый подход позволяет:

• —    обоснованно распределить время на модули, решая прямую и (или) обратную задачи;

• —    оценить, как влияет бюджет времени на успеваемость обучаемых;

• —    корректно осуществлять реструктуризацию рабочей программы;

• —    решать и иные задачи обоснования времени, выделяемого на обучение, с учетом требований, предъявляемых государственными образовательными стандартами.