Тепловое состояние и уровень эрозии катодов сильноточных плазменных систем определяют их функциональные параметры и работоспособность [1]. Наибольший ресурс катодов достигается в режиме термоэмиссии при использовании в качестве электродного материала тугоплавких металлов, активированных легирующими компонентами из окислов редкоземельных элементов [2]. Во время работы плазменного устройства в связи с испарением и выгоранием активаторов происходит эволюция физико-механических свойств материала, что приводит к снижению эксплуатационных характеристик катода. Ресурс данного класса электродов зависит от интенсивности выхода легирующего элемента из объема матрицы основного металла. Поэтому для оптимизации их функциональных режимов необходимо исследование динамики процессов электро- и тепломассопереноса в объеме и на поверхности твердого тела в зависимости от внешних параметров системы, задаваемых условиями экспери- мента и практики.

В данной работе представлены результаты расчетов на основе эволюционной физикоматематической модели катодных и прикатодных процессов (КПП) в сильноточных газовых разрядах [3].

Постановка задачи

Эволюционная физико-математическая модель КПП позволяет исследовать динамику эмиссионных параметров активированных электродов во время работы плазменных устройств. Она основана на решении задачи тепломассопереноса и испарения активаторов совместно с уравнениями, описывающими процессы в системе «твердое тело – поверхность – прикатодная плазма». Ввиду многообразия и сложности КПП в модели они разбиваются на 3 взаимосвязанные группы, выделяя в каждой из них основные процессы.

Процессы в твердом теле описываются системой из трех нелинейных уравнений:

• а)    уравнения теплопроводности

  d T

  
  

  1 d

  
  

  a T

  
  

  a T

  
  

  S T k _ 1 ⁵ i a ⁵ T k      ⁹  .      d T k     2.      .

  ^C k ^p k д = д   r ^ k ^(T k ) д ⁺     ^ k ^(T k ) д + Jk / ^a k ^(T k ) ;

  о t r d r         d r     о z         о z

  
  

  d t

  
  

  r d r

  
  

  d r

  
  

  d z

  
  

• б)    уравнения непрерывности тока

  1 д r 5 r

  
  

  r ^ k ^(T k )

  
  

  a U k d r

  
  

  d

  +-- d z

  
  

  ^ k T )

  
  

  d U k d z

  
  

  = 0,

  
  

н = (jr + j2)1/2,    j =-^. (Tk )dUk / ar,    j =-^k (T wk / dz для катодного узла (k = 1 - катод, k = 2 - обойма), представленного на рисунке;

• в)    уравнения диффузии активатора в катоде

  6 n   1 б таГтА® n

  ⁼ "    r^{D ( T} k

  d t   r о r         о r

  
  

4[D (Г, )Щ 1,  D (Tk) = Doexp(-Q), оz L     оz J                       klk где Tk - температура; ck, pk, Xk, ak - соответственно удельная теплоемкость, плотность, коэффициент теплопроводности, удельная электрическая проводимость материалов катодного узла; jk – плотность тока; Uk – потенциал электрического поля; n, D, D0, Qa – соответственно концентрация, коэффициент диффузии, фактор диффузии, энергия активации легирующего элемента (присадки); k –постоянная Больцмана; t – время. Решение этих уравнений с соответствующими граничными условиями проведено в [4-6].

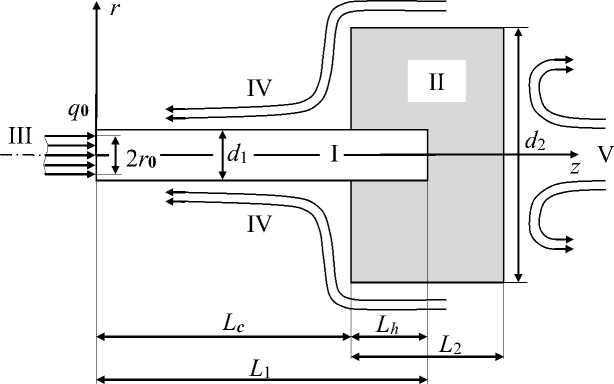
Рис. Схема составного катодного узла плазменных устройств:

I – катод (вставка); II – корпус узла (обойма); III – плазма разряда;

IV – плазмообразующий газ; V – теплоотвод (жидкость)

Уравнения для процессов на поверхности катода, контактирующей с плазмой разряда, представлены в виде:

q 0 + У Г ( ^ эф + 2 kT/ е ) = j_c (1 - 5)(V_C + V - ^ _зф + 2 kT / е ) -

• - S 1 G T ⁴ + q _л + 0,25 a e en e <  v_e >  (2 kT_e / e + ф эф )exp( - eV_C I kT_e );

j” = AT ²exp^{( - е} Ф зф /kT) ,   ^е ф зф = ^e Ф w ^- e ⁽ eE ^)V2;

• I . = 5I = J ( j,- - fj¹*)dF ;

F n V = n V a a        i i *

Процессы в прикатодной области в одномерном приближении описываются следующей системой уравнений:

m k n k v k ⁽ d^v k ¹ dx ) = e k n k E ^- gr^ad Pk - Z w ⁽ v k ^- v ), ^{( k} , ^l = e , i , a );

l ^ k dФi I dx = ~Pnena + an3;

d Ф^ dx = - d Ф _e I dx = d Ф a I dx ,   Ф= n i v i , Ф _e = n e v e , Ф a = n_av_a ;

n i v i ⁺ n e v e = ^j 0 ¹ e = ^COnSt;

P = n a ^kT a ⁺ n e ^kT e ⁺ n i ^kT ;

JTVe = j i V + J O^ V + 2 kTefe ) + 3,2 j_c kTe/e ;

у обр = 0,25 a e en e <  v e >  exp( - eV_c I kT_e ).

В этих уравнениях обозначения общепринятые, они в различных модификациях используются в работах Ли, Гринвуда, Неймана, Зимина, Хвесюка, Мойжеса, Немчинского, Синкевича и др.

В настоящей работе система дополняется уравнением, связывающим эффективную работу выхода электронов со степенью покрытия 0 и распределением концентрации активатора на поверхности электрода:

e^эф (t) = kT(t) !n{^(t) exP [- eTa!kT(t)] + [1 - ^(t)]eXP [- eФм /kT(t)]} , где e^, e^ - соответственно работы выхода электронов матрицы и активатора. Следует особо подчеркнуть, что e^ (t) является основным параметром, управляющим динамикой всей замкнутой системы эволюционной модели КПП.

Решение задачи в обобщенной постановке проведено численными методами, алгоритмы которых представлены в [3].

Метод оптимизации

Катодные узлы генераторов низкотемпературной плазмы (плазмотронов) отличаются большим разнообразием в зависимости от условия эксплуатации и назначения этих устройств [1, 2]. В связи с этим задача оптимизации для катодных узлов сильно усложняется, становится многопараметрической, ее трудно решить прямым перебором варьируемых параметров. При этом основным критерием для оптимизации их рабочих режимов является обеспечение максимального ресурса, включающее в себя требования минимизации уровней удельной эрозии, тепловых потоков, температур и токовой нагрузки катода. С точки зрения практики, решение задач оптимизации является конечной и важнейшей целью исследования КПП в сильноточных плазменных системах. Задача ставится следующим образом.

Исходными параметрами являются только контролируемые в эксперименте и не зависящие от КПП характеристики:

– ток разряда;

– давление и свойства плазмообразующегося газа;

– геометрия и свойства материалов катодного узла;

– условие охлаждения катодного узла.

В число определяемых из расчета входят параметры процессов, методы экспериментального измерения которых достаточно разработаны:

– распределение температуры на катоде;

– распределение работы выхода электронов на катоде;

– тепловой поток в катод;

– плотность тока;

– катодное падение потенциала.

Наряду с этими из теории получаются и другие величины, которые пока не определяются экспериментально (размер прикатодной области, распределение в ней потенциала, температур частиц и т.д.).

При проведении расчетов:

– устанавливаются закономерности КПП, т.е. анализируются функциональные связи между исходными и расчетными параметрами;

– исходя из конкретных условий эксплуатации плазменного устройства, определяется оптимальный режим его работы.

При этом необходимо проводить комплексное сравнение теории с экспериментом в широком диапазоне изменения исходных параметров так, как только согласие между ними может служить критерием по использованию метода для расчета катодных и прикатодных процессов, оптимизации функциональных режимов плазменных систем. Приведем пример практического применения развитого метода.

Плазмотрон ПТП-101 мощностью до 300 кВт предназначен для нагрева различных газов и их смесей. Основные технические данные приведены в таблице 1. Мощность плазмотрона, энтальпия и среднемассовая температура на выходе и напряжение дуги варьируются в широких пределах регулированием рабочего тока и длины канала межэлектродной вставки (МЭВ). Применение пористого пенокордиерита ( ρ = 9 ⋅ 10 ^-5 г/см³) в качестве МЭВ позволяет за счет регенеративного охлаждения повысить тепловой КПД плазмотрона до 0,95 [7].

Таблица 1

Технические характеристики плазмотрона

Рабочий газ	аргон, азот, метан, воздух
Ток дуги, А	100 – 600
Напряжение дуги, В	200 – 1400
Расход газа, г/с
Аргон	8 – 12
Азот	3,5 – 4
Метан	8 – 10
Воздух	36.4 – 50
Тепловой КПД
в аргоне	менее 0,7
в других газах	0,85 – 0,95
Максимальная среднемассовая температура нагреваемого газа, K
Аргон	до 9 ⋅ 103
другие газы	до 4 ⋅ 103
Расход охлаждающей воды, кг/с	1 – 2

Составной катодный узел плазмотрона представляет собой цилиндрическую медную обойму, в которую запрессован или запаян стержень (вставка) из тугоплавкого металла (см. рис.). Исходные геометрические параметры для расчета следующие: L c = 0 – 30 мм, L h = 10 мм, d 1 = 4 – 8 мм, L 2 = 15 мм, d 2 = 30 мм. Размеры медной обоймы фиксированы, а размеры тугоплавкой вставки при оптимизации варьировались в указанных пределах с шагом 0,5 мм по длине и 0,2 мм по радиусу. Теплофизические свойства материалов конструкции аналогичны данным, приведенным в [6], материал катода – лантанированный вольфрам ВЛ-15 (W+1,5% La 2 O 3 ) с исходной работой выхода электронов e φ = 2,96 эВ. В результате серии расчетов была определена по номинальному току оптимальная геометрия катода: L c = 20 мм и d 1 = 5,2 мм.

В таблице 2 представлены данные ресурса работы катода указанной геометрии в среде Аr в зависимости от рабочего тока.

Таблица 2

Ток дуги, А	100	200	300	400	500	600
Расчетный ресурс τ 1 , ч	< 1	3	35	93	6	< 6
Экспериментальный ресурс   τ 2 , ч	< 1	3	32	87	5	< 1

Ресурс работы катодного узла

Из таблицы 2 видно, что наибольший ресурс электрода достигается при рабочем токе 400 А. При этом обеспечивается необходимая номинальная мощность плазмотрона в 250 кВт. В нижней строке приведены результаты контрольных экспериментальных испытаний на ресурс катодного узла при некоторых фиксированных значениях рабочего тока. Расчетный ресурс в таблице дается с округлением до 1 ч, так как в экспериментальных условиях теплофизическое состояние катода фиксировалось с интервалом в 1 ч. Необходимо подчеркнуть, что в расчетах за ресурс принимается время непрерывной работы τ 1 , в течение которого электрод работает без оплавления активной поверхности. Материал катода начинает плавиться, когда прекращается диффузия активатора к рабочей поверхности из глубинных слоев и e φ электрода достигает значения чистого вольфрама. Время τ 1 в общем случае отличается от реального ресурса катода τ 2. Если при токовой нагрузке I > 500 A оплавление приводит к быстрому разрушению структуры катода (здесь τ 1 = τ 2 ), то на малых токах I < 300 A он может работать некоторое время как электрод из чистого вольфрама. Однако последующее увеличение токовой нагрузки до номинальной приводит к быстрому разрушению электрода.

Контрольные испытания показали, что реальный ресурс электродов τ 2 несколько меньше расчетного. Это объясняется тем, что в теоретической модели не учитывалась пусковая эрозия, снижающая работоспособность электродов [2].