Оптимизационное моделирование как инструмент управления экономической безопасностью региона

В экономике на разных уровнях управления возникает необходимость принятия решения при ограниченности ресурсов. Для решения данной проблемы используются оптимизационные модели, направленные на поиск наилучшего варианта из некоторого множества возможных решений. Критерием оптимальности в таких моделях служит достижение экстремального (максимального или минимального) значения некоторой величины, зависящей от переменных модели. Такая величина называется целевой функцией задачи. Смысл целевой функции зависит от вида и смысла решаемой задачи [1].

В качестве инструмента оптимизации наиболее часто используется математическое программирование (линейное, нелинейное, динамическое и т. п.), которое входит в арсенал методов исследований операций [2]. По оптимизационному моделированию написано множество учебных пособий [3-5]. П. Н. Победаш, А. В. Медведев рассматривают вопросы прогнозирования тенденций развития мировой социально-экономической системы и отмечают, что существенным аргументом в пользу применения оптимизационного подхода для моделирования глобального развития служит возможность создания системы поддержки принятия решений [6].

Построим оптимизационную модель для управления экономической безопасностью региона. Под экономической безопасностью будем понимать совокупность условий и факторов, характеризующих текущее состояние экономики, стабильность, устойчивость и поступательность ее развития, степень ее самостоятельности в процессах интеграции с экономикой федерации, что выражается в:

• •    возможности проводить собственную экономическую политику в рамках федерации;

• •    способности безобвально реагировать на резкие геополитические изменения;

• •    способности осуществлять (или начать осуществление) крупные экономические мероприятия (не ожидая помощи от федерации) по неотложным социальновзрывным ситуациям на территории, связанным с локальными экономическими бедствиями или экономическими просчетами (ошибками) на федеральном уровне;

• •    возможности на договорной основе оказывать помощь сопредельным областям, республикам и регионам, где существующая несбалансированная экономическая ситуация может негативно отразиться на экономических интересах территории;

• •    возможности стабильно поддерживать соответствие действующих на территории экономических нормативов общепринятым в мировой практике (или директивно утвержденным для территории на конкретный период времени), что позволило бы сохранить (или восстановить) достойный уровень жизни населения [7; 8].

Для примера расчета выделим виды безопасности, характеризующие состояние основных сфер деятельности региона: инвестиционную, производственную, научно-техническую и рынок труда. В таблице 1 представлен набор индикаторов, описывающих ситуацию по безопасности в выбранных сферах. В рамках исследования использованы индикаторы из Комплексной методики диагностики экономической безопасности, разработанной в Институте экономики УрО РАН [9].

Пусть заданы индикаторы экономической безопасности. Таким образом, имеем многомерный вектор: X = ( Х_х,...,Х_м ) , характеризующий экономическую безопасность регионов. Ему соответствует многомерное пространство фактических значений: x = ( x_x ,..., x_M ) . Для каждого из индикаторов заданы верхние B + или нижние Bj — пороговые уровни. Введем некоторые «разумные»

Таблица 1

Вид безопасности	Обозначение	Индикаторы
Инвестиционная	X1	Отношение объема инвестиций в основной капитал к валовому региональному продукту (ВРП), %
	X2	Темп прироста объема инвестиций в основной капитал по сравнению с предыдущим годом, %
Производственная	X3	Темп прироста объемов промышленного производства по сравнению с предыдущим годом, %
	X4	Степень износа основных производственных фондов (на конец года), %
Научнотехническая	X5	Доля внутренних затрат на исследования и разработки в ВРП, %
	X6	Отношение среднемесячной зарплаты в отрасли «Наука и научное обслуживание» к среднемесячной номинальной начисленной заработной плате, %
	X7	Удельный вес инновационных товаров, работ, услуг в общем объеме отгруженных товаров, выполненных работ, услуг, %
	X8	Доля затрат на фундаментальные исследования во внутренних затратах на науку и научное обслуживание, %
Рынок труда	X9	Уровень общей безработицы, %

Индикаторы диагностики экономической безопасности по выбранным сферам [7]

наилучшие в смысле безопасности значения 0^., характеризующие устойчивое социально-экономическое состояние регионов. Под «разумностью» понимается то, что значения не должны носить идеализированный характер, а отражать реальное социально-экономическое положение. Чем больше разница между значениями 0 j и Bj , тем менее достоверным будет оптимизационное моделирование [10].

Сделаем замену переменных следующим образом.

Если для индикатора безопасности X j задан верхний пороговый уровень B j , то

. = xj 0 j

j"B;-0 j

Если для индикатора безопасности X j задан нижний пороговый уровень B ^- _j , то

zj =

θ j - x j

θ

j

-

B

-

j

В результате замен переменных (1), (2) получили в качестве области допустимых (безопасных) значений положительный сектор гипершара G с центром в начале координат и единичным радиусом. При этом точка (θ 1 , θ 2 ) отобразится в начало координат.

Пусть имеем некоторые фактические значения показателей индикаторов безопасности региона: x0 = (x0, ... ,x0 ) . Очевидно, что при заданном нижнем поро- говом уровне B -j должно выполняться неравенство x0 ≤ θ , а при заданном верхнем пороговом уровне B +j необходимо, чтобы x0 ≥ θ . Невыполнение этих условий говорит о неудачном выборе значений θ , которые должны быть скорректированы. Корректировку, например, можно сделать путем приравнива-0

ния θ = x в каждом таком случае.

Опишем следующую задачу.

Задача 1. Оценка фактического состояния по безопасности региона.

Эту задачу можно решить, представив фактические значения индикаторов безопасности в виде расстояния от точки x ⁰ = ( x ⁰, ..., x ⁰ ) до области G .

Вначале сделаем замену переменных (1),  (2) и получим вектор

00  0         0

z = (z , ..., z ) . Считаем, что ∀j z ≥ 0 .

Затем решаем оптимизационную задачу нелинейного программирования

M r(z0) = arg min 3 ∑(zj z∈R V j=1

-z0j)2 ,

M

∑ z ² j ≤ 1 , j = 1

zj ≥0, j=1,2,...,M.

Результатом решения задачи (3) — (5) будет вектор: z ^∗ = ( z ^∗ , ..., z ^∗ ) .

M

Если точка z ∉ G (т. е. ∑(zj ) ≥ 1), то имеет фактическое значение ин- j=1

M декса опасности r(z0) = ∑(z∗j ) .

j = 1

M

В противном случае, когда Z G G (т. е. £ ( z * ) ² <  1 ), имеем безопасную j = 1

ситуацию, которую будем оценивать через отрицательные величины, т. е.

M

r (z 0) —^ (z )

J - 1

Замечание 1. Можно рассмотреть вопрос введения весовых коэффициентов в задаче (3). Тогда целевая функция (3) прим ет вид:

M

r(z0) — argmin a .^(z . — z?1)2 ■ zeRM^ j     j    j

Введение весовых коэффициентов означает разную «опасность» выбранных индикаторов. Это требуется каким-то образом обосновать.

Замечание 2. После решения задачи (3) — (5), сделав обратную замену, от вектора Z * — ( z * ,..., z^ ) перейдем к вектору фактических значений индика-

* z *          * Х торов безопасности X — (x1,..., хм ) :

• •    если задан нижний пороговый уровень B j , то x j — Оу — z у( ° j - B 7 ) , • если задан верхний пороговый уровень B j , то xj — Оу + zj ( B у — О^ ) ■ Замечание 3. Если Z ⁰ ^ G , то значения компонент вектора X * — ( X ** ,..., X^ ) можно рассматривать в качестве решения задачи целевого управления, в результате которого показатели факторов риска региона выйдут на допустимый уровень.

Замечание 4. Задачу (3) — (5) можно достаточно просто решить без программирования, воспользовавшись средством «Поиск решения» в MS Excel.

В таблице 2 представлен пример расчета индекса опасности как интегрального показателя, позволяющего оценивать уровень опасности для данного набора индикаторов.

Замечание 5. Отметим, что можно задавать одновременно нижние и верхние

B 7+ B+ пороговые уровни. В этом случае будем считать, что О —---------. Для пе- j       2

ременных с двумя ограничениями Bj и B ⁺ в задаче (3) не нужно накладывать ограничения неотрицательности (5). Вместо замен (1), (2) имеем

z — 2 j j    B+

—

—

^O j B -

.

На рисунке 1 представлены расчеты индекса опасности для Свердловской области при трех вариантах выбора индикаторов. В первом варианте используются восемь индикаторов, исключается уровень общей безработицы. Во втором вари- анте данным индикатор включен в расчет индекса опасности. Для третьего варианта исключается удельный вес инновационных товаров, работ, услуг в общем объеме отгруженных товаров, выполненных работ, услуг.

Таблица 2

Пример расчета индекса опасности по выбранному набору индикаторов для Свердловской области за 2016 г.

Индикатор	2016	Z0	Z*	X*	Пороги	Оптим. значения
X1	18,13	0,88	0,03	23,83	17,3	24
X2	-8,9	1,36	0,45	13,82	0	25
X3	7,7	0,69	0,43	14,15	0	25
X4	57,1	1,71	0,38	43,77	50	40
X5	1,55	0,75	0,24	1,7	1,48	1,77
X6	1,57	0,85	0,27	1,87	1,5	2
X7	8,4	0,45	0,49	8,35	7,67	9
X8	12,05	0,08	0,25	10,11	1,33	13
X9	6,2	0,12	0,25	6,66	9,27	5,8
Ограничение	1,02
Целевая функция	4,04
Индекс опасности r(Z0)	2,01

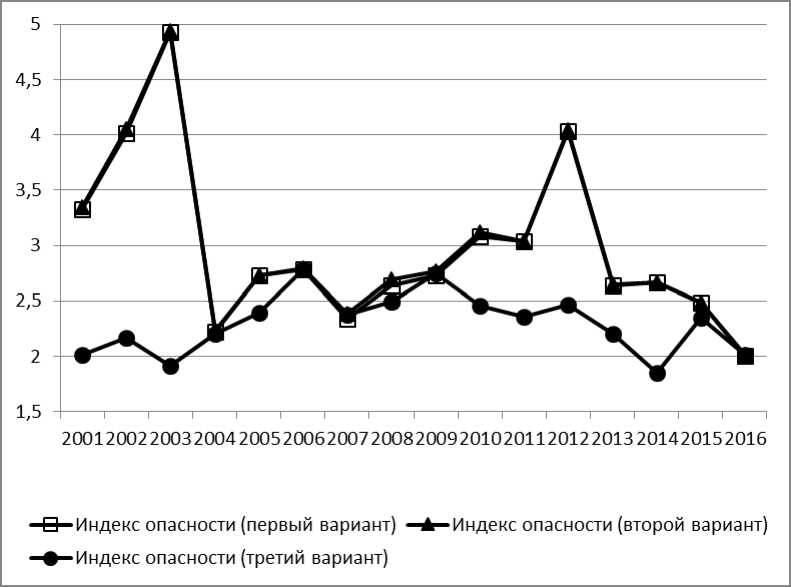
Рис. 1. Динамика изменения индекса опасности для выбранных индикаторов в Свердловской области (по трем вариантам)

Как показали результаты расчетов, изменение индекса опасности для двух вариантов выбранных индикаторов наблюдается в период 2008–2010 гг. Это характеризует сложившуюся в данный период социально-экономическую обстановку, когда уровень общей безработицы был высоким.

Пики индекса опасности в 2003 и 2012 гг. определяет индикатор «Удельный вес инновационных товаров, работ, услуг в общем объеме отгруженных товаров, выполненных работ, услуг» (рис. 2). В указанные годы данный индикатор имел низкие фактические значения, которые были ниже оптимальных в 2 и более раза.

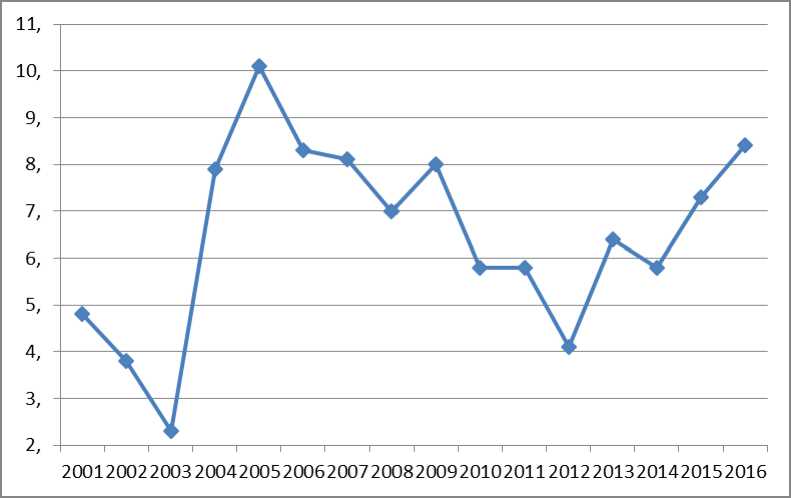
Рис. 2. Удельный вес инновационных товаров, работ, услуг в общем объеме отгруженных товаров, выполненных работ, услуг в Свердловской области за период 2001–2016 гг., %

Примечание. График построен по данным Федеральной службы государственной статистики.

При расчетах индекса опасности по третьему варианту индикатор удельного веса инновационных товаров, работ, услуг в общем объеме отгруженных товаров, выполненных работ, услуг, исключен (рис. 1). В динамике индекса опасности уже можно проследить нарастание кризисных явлений в состоянии экономической безопасности в период 2007–2009 гг.

Решение поставленной в исследовании задачи позволяет:

• –    диагностировать, при каких оптимальных значениях всех индикаторов возможно получить наиболее низкое значение индекса опасности;

• –    анализировать динамику изменения индекса опасности по годам;

• –    оценить вклад того или иного индикатора при данных пороговых и оптимальных значениях в общую ситуацию.

Статья выполнена в соответствии с планом НИР ФГБУН Института экономики УрО РАН на 2018–2020 гг.