Особенности моделирования и оптимизации комплекта новых логических элементов ПЛИС
Автор: Вихорев Р.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Информатика. Информационные системы
Статья в выпуске: 3 (42), 2018 года.
Бесплатный доступ
Функциональные возможности и области применения программируемых логических интегральных схем (ПЛИС) постоянно расширяются, в том числе в специальной аппаратуре. Имеются два основных вида ПЛИС: FPGA (Field-Programmable Gate Array) и CPLD (Complex Programmable Logic Device), отличающиеся принципами реализации логики и хранения конфигурационной информации. Тем не менее, различия между ними постепенно нивелируются: так, в продуктах фирмы Интел ПЛИС FPGA, имеющие конфигурационную флэш-память отнесены к CPLD, хотя логические элементы типичны для FPGA, в которых используется оперативная память, требующая загрузки при включении питания. На этом фоне отмечаются попытки комплексирования двух подходов к реализации логики и создания гибридных ПЛИС. В статье анализируются особенности моделирования и оптимизации комплекта новых логических элементов ПЛИС для реализации систем функций.
Моделирование, оптимизация, логический элемент, транзистор
Короткий адрес: https://sciup.org/147245383
IDR: 147245383 | УДК: 681.32 | DOI: 10.17072/1993-0550-2018-3-111-116
Текст научной статьи Особенности моделирования и оптимизации комплекта новых логических элементов ПЛИС
В ПЛИС [1] логические функции реализуются двумя основными путями. В ПЛИС FPGA используются генераторы функций, называемые Look Up Table (LUT) [2], которые реализуют одну произвольную функцию z от n переменных х ( n = 3, 4; в современных адаптивных логических модулях – АЛМ n может быть = 8) в совершенной дизъюнктивной нормальной форме в виде дерева:
Поэтому реализация функций большого числа переменных n проблематична, а для получения системы из m функций необходимо m деревьев (1). В ПЛИС CPLD реализуется иная технология – программируемых логических матриц (ПЛМ), которые ориентированы на ДНФ-реализацию систем функций большого числа переменных [3, 4]. Так, матрица конъюнкций (матрица И) может быть описана выражением:
z ( xnxn - 1... x 2 x 1) = dout •
x n ←
xn - 2 ← .
x n - 1 ← xn - 2 ←
x ← xn - 2 ← x n - 1 ← xn - 2 ←
x ←xn-2← xn ←xn-1←xn-2← xn-1←xxn-2←
x ← x 1 ⋅ d 0 x 2 ← x 1 ⋅ d 1
, (1)
x xn y1(xnxn-1...x2x1) = n ⋅ s1.n s1.n
• x n - 1 s 1. n - 1
x n - 1
s 1. n - 1
n - 2←..... x ←
..... 2 x
x 1 ⋅ d 2 n x 1 ⋅ d 2 n
2 n - 2
2 n - 1
где d – биты настройки 22 функций в совершенной дизъюнктивной нормальной форме (СДНФ), всего 2 n бит.
x x 2 x x 1
⋅•⋅ s1.2 s1.2 s1.1 s1.1
x x 2 x x 1
⋅•⋅ s2.2 s2.2 s2.1 s2.1
f1(xnxn-1...x2x1) =y1(xnxn-1...x2x1)q1.1 ∨y2(xnxn-1...x2x1)q1.2∨....∨yk(xnxn-1...x2x1)q1.k f2(xnxn-1...x2x1) =y1(xnxn-1...x2x1)q2.1∨y2(xnxn-1...x2x1)q2.2∨....∨yk(xnxn-1...x2x1)q2.k fµ(xnxn-1...x2x1) =y1(xnxn-1...x2x1)qµ.1 ∨y2(xnxn-1...x2x1)qµ.2∨....∨yk(xnxn-1...x2x1)qµ.k fm(xnxn-1...x2x1) =y1(xnxn-1...x2x1)qm.1∨ y2(xnxn-1...x2x1)qm.2∨....∨ yk(xnxn-1...x2x1)qm.k,
(3) где y – конъюнкции от n переменных ( k штук), f – функции (m штук) s – настройка конъюнкций, q – настройка функций. Соответственно, здесь нет степенной зависимости сложности от n .
Хотя в современных АЛМ FPGA [5, 6] реализуются все возможные функции до 6 переменных и некоторые функции 7 и 8 переменных, им не сравниться с возможностями реализации систем функций нескольких десятков переменных в ПЛИС CPLD. Оба подхода имеют свои преимущества и недостатки, поэтому имеется тренд создания гибридных ПЛИС [7, 8]. Однако в полной мере это направление не проработано. Рассмотрим особенности моделирования и оптимизации логики в рамках новых предлагаемых подходов [9– 12]. Полученные формулы сложности в количестве транзисторов не дают полной картины, без оценки тока потребления в статическом и динамическом режимах невозможно оценить эффективность предложенным решений.
На рис. 1. изображен известный DC LUT на одну переменную с резисторами по выходам – DC-LUT-R.
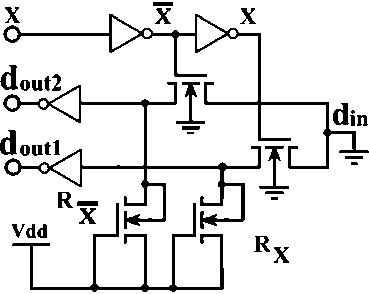
Рис. 1. Известный DC LUT на одну переменную с резисторами по выходам – DC-LUT-R
Первый предлагаемый вариант – по каждому транзистору соответствующего уровня дерева (потранзисторно) выражение (6):
xn ( ∨ xd in ) →
x n - 1 ( ∨ xn - 1 d in ) → . xn - 1 ( ∨ x n - 1 d in ) →
→ x 1( ∨ x 1 din ) → d 0 . x 1( ∨ x 1 din ) ⋅→ d 1
d in •
x n ( ∨ xnd in ) →
и – рис. 2:
x n - 1 ( ∨ xn - 1 d in ) → xn - 1 ( ∨ x n - 1 d in ) →
x 1( ∨ x 1 din ) ⋅→ d 2 n - 2 x 1( ∨ x 1 din ) →⋅ d 2 n - 1
1. Усовершенствованный метод реализации систем функций в СДНФ и моделирование соответствующих элементов
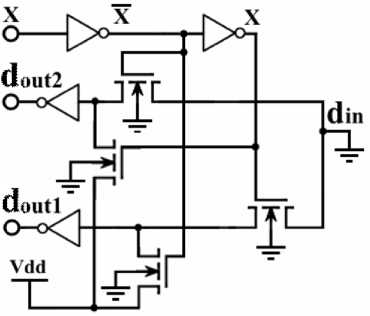
Рис. 2. DC LUT на одну переменную с отдельными транзисторами ортогональности
Предлагается использование дерева (1) FPGA "наоборот" для дешифрации входного
набора
xn →
xn - 2→ x 1 →⋅ d 0
xn-1 → x2 → xn-2→ x1⋅→d1
x →xn-2→ n-1 xn-2→
d in
•
x -1 →xn-2→ xn-2→ xn → xn-2→ xn-1 →x
Второй вариант – с блоком конституент нуля (BKN) f и n транзисторами ортогональности по последнему транзистору (по выходу реверсивного дерева) – выражение (7) [9, 10].
n - 2 → .
x 1 ⋅→ d n
► ^ ^
2 n - 1
x 1( ∨ f 0 din ) → d 0
xn - 1 →........→ x 1( ∨ f 1 din ) ⋅→ d 1
x n → x n - 1 →
Для обеспечения ортогональности по
d • in
выходам используются подтягивающие резисторы R, негативно сказывающиеся на энергоэффективности:
x n → x n - 1 → x n - 1 →
→ x 1( ∨ f 2 n - 2 din ) ⋅→ d 2 n - 2
.............. x 1( ∨ f 2 n - 1 din ) →⋅ d 2 n - 1
d • in
x n - 1 →
x→ n xn-1 →
→ x 1 →⋅ ( R ) d 0 x 1 ⋅→ ( R ) d 1
x n → x n - 1 → x n - 1 →
Во всех случаях реализация дизъюнкций конституент одинакова:
2n zl = ∨(dout.i ⋅hl.i);l=1, m, (8)
i = 1
x 1 ⋅→ ( R ) d n
-
. → 2 - 2
x 1 →⋅ ( R ) d 2 n -1
где h – настройка вхождения конституенты i в данную l-ую из m функций системы.
Моделирование [13] показало, что гипотеза о существенном снижении энергопотребления при отказе от подтягивающего резистора в логических элементах (5)-DC-LUT-R, реализующих системы функций в СДНФ и ДНФ, полностью подтвердилась. Кроме того, энергопотребление варианта (7)-DC-LUT-BKN оказалось существенно меньше, чем у варианта (6) – DC-LUT-O и, соответственно, меньше, чем у m блоков LUT – рис. 3.
При этом для обеспечения ортогональности также используются подтягивающие транзисторы R в матрице И:
x x n x x n - 1
y1(xnxn-1...x2x1)=(R1) n ⋅ • n-1 ⋅ • s1.n s1.n s1.n-1 s1.n-1
x x n x x n - 1
y2(xnxn-1...x2x1)=(R2) n ⋅ • n-1 ⋅ • s2.n s2.n s2.n-1 s2.n-1
x x n x x n - 1
yj(xnxn-1...x2x1)=(Rj) n ⋅ • n-1 ⋅ • sj.n sj.n sj.n-1 s j.n-1
x x2 x x1 .⋅•⋅ s1.2 s1.2 s1.1 s1.1
x 2 ⋅ x 2 • x 1 ⋅ x 1 (11)
s 2.2 s 2.2 s 2.1 s 2.1
x x 2 x x 1
.⋅•⋅ sj.2 sj.2 sj.1 sj.1
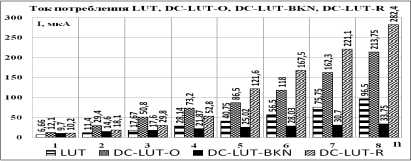
Рис. 3. Ток потребления логических элементов для разного количества входных переменных при напряжении питания 0,8 В на частоте 300МГц; количество реализуемых логических функций m=3
Кроме того, предлагается адаптивный логический элемент [14], который может реализовывать либо LUT, либо DC-LUT:
x n - 2
xn - 1 x n - 2
x n
x 1 ⋅ ( s ⋅ d ∨ s ⋅ [ = z ])
2 n - 1 0
” x • ( s • d v s • [ = z, ])
1 2 n - 1 + 1 1
(din ■ s v zout (xn - x1) • s) • xn-2 xn-1xn-2
xn-2 xn-1x n-2
x n - 2 x 1 ⋅ ( s ⋅ d 2 n - 1 - 2 ∨ s ⋅ [ = z 2 n - 2 ])
xn - 1 xn - 2 - x 2 x^s • d2n - 1 — 1 v s • [ = z 2 n — 1]).
В выражении (9) с целью упрощения не указаны средства обеспечения ортогональности. Настройка на реализацию дешифратора осуществляется конфигурационной константой s. Это позволяет реализовать дешифратор набора n переменных на одном LUT вме- сто2 n LUT. При этом возможная требуемая реализация дизъюнкций конституент может быть возложена на штатные коммутационные средства ПЛИС.
2.Усовершенствованный метод реализации систем функций в ДНФ и моделирование соответствующих элементов
Существующая в ПЛИС типа CPLD реализация конъюнкций (2) может быть описана следующим образом по j -й переменной с использованием конфигурационной константы s:
y^xn...x 2 X1) = ( xi v sj.)(xv Sjj) (10)
x xn xx yk(xnxn-1...x2x1)=(Rk) n ⋅ • n-1 ⋅• sk.n sk.n sk.n-1 sk.n-1
x 2 x 2 x 1 x 1
⋅•⋅, sk.2 sk.2 sk.1 sk.1
Предложено новое выражение для обеспечения ортогональности:
si =(dSRAM.i⋅din ∨dSRAM.i⋅d0)⋅xi∨
∨ (d SRAM. i ⋅ d in ∨ d SRAM.i ⋅ d 0 ) ⋅ x i ;i = n;
где d SRAM.i , d SRAM.i – настройки соответствующих ячеек конфигурационной памяти.
Соответствующий блок одной переменной приведен на рис. 4.
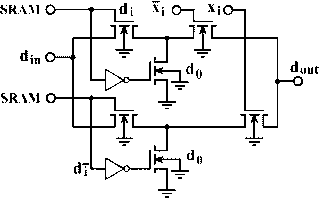
Рис. 4. Блок одной переменной по выражению (12)
Это позволяет обеспечить передачу заданного логического уровня при "правильном" значении переменной и противоположного уровня при "неправильном" значении для последующего формирования значения запрограммированной конъюнкции. В случае несущественности переменной обеспечивается передача заданного логического уровня. При этом в известном методе DNF-R образуется обрыв цепи, как раз и парируемый подтягивающим транзистором. Предложено два варианта формирования значения конъюнкции по значениям (12) – параллельный DNF-S, DNF-P.
При моделировании оказалось, что логический элемент, реализующий ДНФ с последовательным соединением блоков настройки переменных DNF-S, имеет существенно меньший ток потребления, чем с параллельным DNF-P и, конечно, DNF-R (рис. 5).
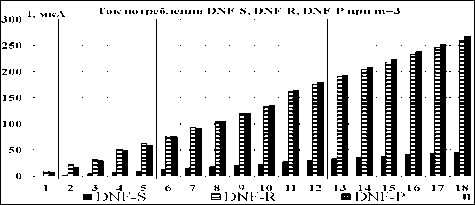
Рис. 5. Ток потребления логических элементов ДНФ для разного количества входных переменных n, при напряжении питания 0,8 В на частоте 300МГц; количество реализуемых логических функций m=3
3. Оптимизация комплекта новых логических элементов ПЛИС
Элементы оцениваются по сложности относительно заданного набора парамет-ров n , m , w , k , r , где n – число переменных m – число функций, w – число конъюнкций для ДНФ, k – параметр декомпозиции дерева LUT (как правило k =1, т. е. дерево для большого числа переменных строится из деревьев на одну переменную), r – ограничения Мида-Конвей (максимально возможное число последовательно соединенных передающих транзисторов, r =4, но в ПЛИС по оценкам специалистов это параметр равен 3; после трех транзисторов обязательно устанавливается так называемый восстановитель уровня сигнала).
Дано: архитектура существующего адаптивного логического модуля – АЛМ, e множество элементов АЛМ: ∪ Ψ , их коли-i=1 i
e чество: = ∑ Ψi , (сейчас, например, как в i=1
StratixIII e =8; LUT3 – 4 штуки, LUT3 – 2 штуки); исходные значения сложности существующих логических элементов FPGA и CPLD:
e Ψ ξ
L – ∑∑ L ( n , m , w , k , r ) i ξ ; энергопотребле- i = 1 ξ = 1
e J Ψµ ния E – ∑ ∑ Eµ(n,m,w,k,r)iµ и макси-i=1 µ=1
мальной задержки max τ Ψ .
Минимизируется сложность набора элементов в новом предлагаемом АЛМ на основе получения оценок сложности и модифицирования венгерского метода (алгоритма) [15–17] с целью получения оптимального набора (вектора, комплекта) элементов [ z 1 z 2.... z π ] :
Lz z2 z ( n , m , w , k , r ) → min; (13)
[ z 1 z 2 z π ]( n , m , w , k , r ); z λ =
ν π e
= ∑ ψ σ ; ψ σ ∈ Ψ i * ; ν ≤ j ; ∑ z = ∑ Ψ i
σ = 1 κ = 1 i = 1
С использованием полученных наборов [ z 1 z 2 .... z π ]( n , m , w , k , r ) определить множество Парето, учитывающее полученные в результате моделирования оценки энергопотребления и задержки и их интерполяцию для реальных значений параметров систем логических функций.
В результате получить требуемое количество новых элементов в одном АЛМ*:
q
∑ I Ψ* j I j = 1
так, чтобы с меньшими затратами в количестве транзисторов реализовать задан- ные системы логических функций q I ΨγI eIξ I
∑∑ L *( n , m , w , k , r ) j γ << ∑∑ L ( n , m , w , k , r ) i ξ ; (15 ) j = 1 γ = 1 i = 1 ξ = 1
при этом не ухудшить энергопотребление и задержку:
q JΨ γ e J Ψ ξ I
∑∑ Ε ( n , m , w , k , r ) j γ ≤ ∑∑ Ε ( n , m , w , k , r ) i ξ ; j = 1 γ = 1 i = 1 ξ = 1
∀ τ * ∀ τ Ψ (max τ * ≤ max τ Ψ ). Ψ j i Ψ j i
Результаты оптимизации представлены на рис. 6.
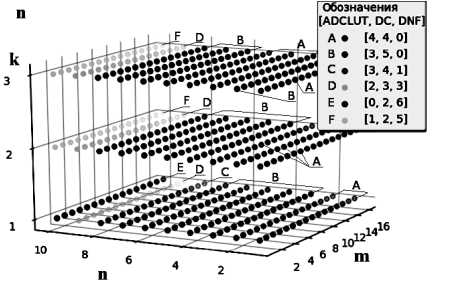
Рис. 6. Результаты оптимизации логических элементов
Выводы
Таким образом, при большом числе переменных целесообразно введение большего числа блоков ДНФ; такие АЛМ подходят для ПЛИС высокой ценовой категории. При среднем значении числа переменных и функций достаточно введение блоков АDC-LUT.
Для бюджетных ПЛИС достаточно введения примерно одинакового количества АDC-LUT и DC-LUT.
Задача решалась в общем виде относительно параметров, указанных в открытых источниках. Разработанный алгоритм может быть использован для получения решений с учетом других доступных параметров существующих ПЛИС.
В дальнейшем целесообразно оценить и площадь кристалла для уточнения результатов оптимизации.
Список литературы Особенности моделирования и оптимизации комплекта новых логических элементов ПЛИС
- Угрюмое Е.П. Цифровая схемотехника: учеб. пособие. 2-е изд., перераб. и доп. СПб.: БХВ-Петербург, 2007. 782 с.
- Строгонов А., Цыбин С. Программируе мая коммутация ПЛИС: взгляд изнутри. URL: http://www.kite.ru/articles/plis/2010-_11_56.php (дата обращения: 11.06.2017).
- PLA. URL: https://tams-www.informatik.uni-hamburg.de/applets/hades/webdemos/42-programmable/10-pla/pla.html (дата обращения: 27.06.2018).
- FPGA/CPLD - ПЛИС (Программируемые Логические Интегральные Схемы). URL: http://www.fpga-cpld.ru/ (дата обращения 02.07.2018).
- Logic Array Blocks and Adaptive Logic Modules in Stratix III Devices. URL: https://www.altera.com.cn/content/dam/altera-ww/global/zh_CN/pdfs/literature/hb/stx3/stx3_ siii51002.pdf (дата обращения: 29.06.2018).
- Обзор архитектуры ПЛИС семейства Virtex-5. URL:http://elektors.ru/radioelekt-ronika/mikroshemy/2759-obzor-arhitektury-plis-semeystva-virtex-.html (дата обращения: 27.06.2018).
- Chi Wai, Yu. Hybrid FPGA: Architecture and Interface. URL: https://sydney.edu.au/engineering/electrical/people/philip.leong/UserFiles/File/theses/cwyu10.pdf (дата обращения: 28.06.2018).
- Alireza Kaviani and Stephen Brown. HYBRID FPGA ARCHITECTURE. URL: https://sydney.edu.au/engineering/electrical/people/philip.leong/UserFiles/File/theses/cwyu10.pdf (дата обращения: 21.06.2018).
- Программируемое логическое устройство: пат. Рос. Федерация / Тюрин С.Ф., Вихорев Р.В.; - № 2573732; Опубл. 27.01.2016, Бюл. № 3.
- Тюрин С.Ф., Вихорев Р.В. Усовершенствованный метод реализации в FPGA систем логических функций, заданных в СДНФ // Инженерный вестник Дона. 2017. Т. 44, № 1(44). С. 39.
- Вихорев Р.В., Тюрин С.Ф. Программируемые логические элементы ПЛИС FPGA для реализации систем логических функций // Вестник Пермского национального исследовательского политехнического университета. Электротехника, информационные технологии, системы управления. 2017. № 3(23). С. 133-145.
- Tyurin S., Grekov A., Vikhorev R., Prokhorov A. Advanced FPGA Look up tables. International Journal of Pure and Applied Mathematics. 2017. Vol. 117, № 22. P. 143-147.
- Вихорев Р.В., Прохоров А.С., Тюрин С.Ф., Никитин А.С. Моделирование и оптимизация инновационных логических элементов ПЛИС // Вестник Пермского национального исследовательского политехнического университета. Электротехника, информационные технологии, системы управления. 2017, № 24. С. 192-208.
- Тюрин С.Ф., Вихорев Р.В. Адаптивный логический модуль ПЛИС с архитектурой FPGA // Вестник Рязанского государственного радиотехнического университета. 2018, № 63. С. 69-76.
- Вихорев Р.В., Прохоров А.С., Скорнякова А.Ю., Тюрин С.Ф. Усовершенствованные методы реализации программируемой логики / в сб.: Управление большими системами. УБС-2017, матер. XIV Всерос. школы-конф. молодых ученых. 2017. С. 306-315.
- Тюрин С.Ф., Никитин А.С., Вихорев Р.В., Скорнякова А.Ю. Выбор набора конфигурируемых логических элементов с использованием венгерского метода // Вестник Пермского университета. Математика. Механика. Информатика. 2017. № 2(37). С. 65-68.
- Свидетельство о государственной регистрации программы для ЭВМ № 2017663289 Программа оптимизации набора логических элементов модифицированным венгерским методом "ВЕННИТ" / заявитель и правообладатель Тюрин С.Ф., Никитин А.С., Вихорев Р.В., Скорнякова А.Ю., Прохоров А.С.; - № 2017619911. Заявл. 04.10.2017; Опубл. 28.11.2017.


