Особенности моделирования плазменного синтеза унс в жидкой среде

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License термоустойчивость и др.). Кроме того, фуллерены используются в смазочных материалах для создания защитных пленок, снижающих трение, что позволяет значительно увеличивать срок службы оборудования. Нанотрубки применяются для хранения энергии, фильтрации воды, тонкопленочной электроники, покрытий стойких к температурным перепадам и механическим повреждениям, а также в производстве чувствительных сенсоров и дисплеев с высокой четкостью изображения [1].

Одним из вопросов промышленного синтеза УНС, является нахождение технологических условий получения, обеспечивающих высокий выход определенных однородных структур. Среди простых методов получения качественных УНС значимую роль играют плазменные методы, основанные на сублимации углерода низкотемпературной плазмой с последующей реагрегацией в холодной области [2].

Одним из перспективных методов получе- ния качественного продукта является электроду-говой синтез в жидкой среде с использованием катализатора [3]. Данный метод синтеза позволяет получать несколько различных типов УНС: фуллерены; одностенные и многостенные нанотрубки; нановолокна; нанорога; квантовые наноструктуры; окисленный графен и аморфный углерод (рисунок 1).

Получаемые УНС отличаются молекулярной структурой и соответственно свойствами, представляющие интерес для промышленности.

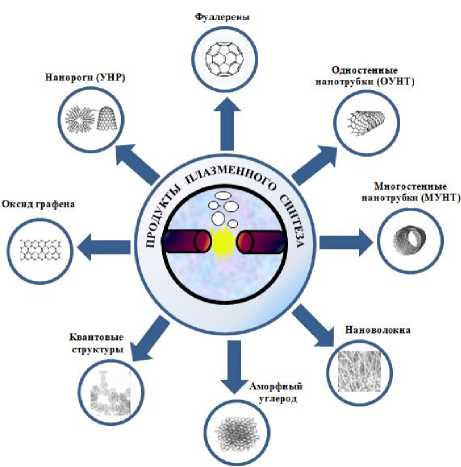
Рисунок 1. Материалы, получаемые электродуговым методом в жидкой среде

Figure 1. Materials produced by electric arc method in liquid medium

Фуллерены олицетворяют собой молекулы, состоящие из атомов углерода, соединенных в пентагоны и гексагоны ковалентными связями С–С и С = С, число которых четно и может изменяться от 24 и более 600. Наиболее стабильными и соответственно перспективными для использования в промышленности являются фуллерены С60 и С70. Фуллерен С70, отличается от С60 вставкой полосы из 10 атомов углерода в экваториальную область С60, из-за чего молекула С70 оказывается более вытянутой. Фуллерены, содержащие более 70 атомов углерода, имеют более сложный изомерный состав [4].

Одностенные (ОУНТ) и многостенные (МУНТ) углеродные нанотрубки представляют собой вытянутые структуры

Короткая, неправильной формы закрытая углеродная нанотрубка, вершиной которой является наноконус, представляет собой нанорог.

Квантовые наноструктуры – это наночастицы размером от 2 до 10 нм, имеющее высокий квантовый выход фотолюминесценции в обратном направлении излучению.

Цель работы – рассмотреть рациональный метод синтеза УНС и возможность оценки влияния технологических условий на него, позволяющих найти условия, обеспечивающие высокий выход и однородность конечного продукта в промышленных масштабах, повысить эффективность процесса.

Результаты

Предлагаемая установка плазменного синтеза УНС представляет собой камеру, внутри которого создается электродуговой разряд. Для создания дуговой разрядки используются два электрода, на которые подается электрический ток. Катод изготавливается из материала, устойчивого к высоким температурам и коррозии. Анод представляет собой графитовый электрод с высокой степени очистки от различный примесей, содержащий катализатор.

На выход и качество получаемого продукта, влияет множество факторов: катализатор, вид и параметры тока, температура, давление, размеры реакционной камеры, межэлектродное расстояние, скорость движения анода, расположение, соотношение геометрических размеров электродов и др.

Поэтому установка синтеза должна быть оснащена автоматизированной системой контроля и регулирования необходимых технологических параметров: температура жидкой среды в камере, плотность тока межэлектродного разряда, напряжение на электродах, межэлектродное расстояние, что позволяет обеспечивать стабильные условия протекания реакции [5].

Рассматриваемый процесс синтеза УНС начинается с подготовки катализаторной смеси, непосредственно влияющей на выход, форму и размером наночастиц. Катализатор вводится непосредственно в анодный электрод, размещенный в камере синтеза. На электроды подают напряжение и поддерживают постоянный ток. Плотность поддерживаемого тока зависит от межэлектродного промежутка, параметров электродов и непосредственно влияет на синтезируемые УНС. В межэлектродном пространстве образуется низкотемпературная плазма. При использовании жидкой среды вокруг плазмы дугового разряда создается газообразная среда в виде пузыря. Давление, состав и объем пузыря также влияют на размер формируемых частиц. При этом катод окруженный жидкостью, испытывает интенсивное охлаждение, что существенно влияет на конечный продукт. В условиях высокой температуры, скоростей, давления атомы и ионы реагентов конденсируясь, образуют наночастицы, которые при разных условиях синтеза могут осаждаться на катоде (депозитный осадок) или стенках реакционной камеры давая разный выход и качество.

Схема получения УНС данным способом представлена на рисунке 2.

Камера синтеза

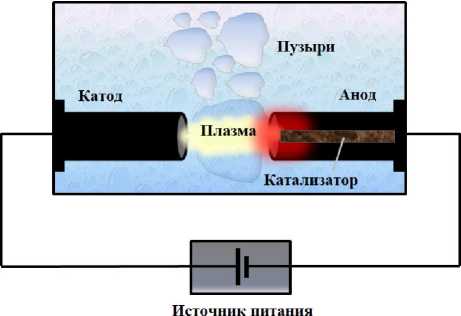
Рисунок 2. Схема получения УНС методом плазменной возгонки графитового сырья в жидкой среде

Figure 2. Scheme for production of CNTs by plasma sublimation of graphite feedstock in liquid medium

Синтезу УНС в жидкой среде присутствуют существенные отличая от использования газовой буферной среды (гелий, аргон и др.):

─ межэлектродное расстояние, зона плазмы, а также необходимый ток между электродами в жидкой среде значительно меньше, чем в газовой буферной среде;

─ вокруг электрической дуги создается газообразная среда в виде пузыря (при использовании дистиллированной воды пузырьки в основном состоят из паров углерода, водяного пара, водорода и окиси углерода), состав и объем которого влияют на размер синтезируемых наночастиц, граница раздела газа и жидкости в пузырьке действует как стенка контейнера;

─ катод окружённый жидкостью испытывает более интенсивное охлаждение, чем в газовой буферной среде, что увеличивает скорость осаждения образованных в плазме кластерных групп углерода формирующих УНС; быстрое изменение температуры непосредственно влияет на рекомбинацию ионов, присутствующих в канале разряда, а граница раздела газа и жидкости в пузырьке, действует как стенка контейнера.

Технологически синтез УНС на основе возгонки графита плазмой дугового разряда в жидкой среде схож с процессом подводной электродуговой сварки. Однако условия синтеза, использование жидкой среды с низкой удельной электропроводность (например, дистиллированная вода), протекание процессов в плазме с присутствием среды газообразного пузыря и катализатора, испарение графитового сырья и конденсация углеродных кластеров, существенно отличают данный метод от процессов сварки [6].

Нахождение условий проведения такого процесса экспериментальными исследованиями малоэффективно и затруднительно. Поэтому для определения рациональных технологических параметров синтеза необходимо использовать методы имитационного моделирования процессов.

Применение фундаментальных законов физики и химии для моделирования процессов, осложнено тем, что в плазме происходит одновременно множество взаимодействующих фазовых и структурных переходов с определенными особенностями, разделить которые зачастую невозможно. Поэтому для описания использовать существующие модели не представляется возможным.

Математическое моделирование таких процессов является сложной ресурсоемкой задачей. Для этого, возможно использовать подходы разных уровней иерархической детализации компонентов, дающих разную точностью описания объекта. Методы, позволяющие описать плазменные процессы, представлены на рисунке 3.

Обозначенные методы математического моделирования процессов получения УНС условно можно разделить на классические, полуклассические и квантово-механические. Они отличаются помимо степени детализации и точности описания объекта, также возможностями учета специфики физических процессов, происходящих в плазме (движение, столкновение, взаимодействие частиц) и вычислительными затратами необходимыми для численного решения задачи [7].

Точные

Точность описания

Приближенные

Шредингеровские модели

1 нм

Высокие

Квантово кинетические модели

(кинетическое уравнение Больцмана, квантомеханическое уравнение Лиувилля)

Метод Монте-Карло

Магнитогидродинамические модели

Диффузионно-дрейфовые модели

Метод одночастичного приближения

100 нм

200 нм

300 нм

400 нм

500 нм

600 нм

s

S s

=

5'

Вычислительные затраты

Низкие

Рисунок 3. Методы математического моделирования процессов синтеза УНС

Figure 3. Methods of mathematical modeling of CNS synthesis processes

Классическим моделям требуются малые вычислительные затраты, однако они обеспечивают низкую точность математического описания объекта и не позволяют детализировано рассматривать процессы взаимодействия в плазме. Полуклассические модели обеспечивают приемлемый компромисс между вычислительными затратами и точностью описания физических явлений, но не дают возможность исследовать процессы на атомном уровне, которые необходимы для понимания формирования УНС в плазме. Использование квантомеханического подхода, обеспечивает высокую точность описания нужных событий в плазме, но создает сложности в построении модели и требует очень больших вычислительными затрат при численном решении [8, 9].

Наиболее подходят для моделирования динамики низкотемпературной плазмы применительно к рассматриваемому синтезу УНС два подхода разных уровней детализации:

─ магнитогидродинамическая (МГД) теория (рассматривающая плазму как проводящую жидкость, обладающая особыми свойствами);

─ кинетическая теория (оперирующая с функцией распределения заряженных частиц по координатам и импульсам) [10].

Условием применимости МГД описания является редкая плазма, в которой нет влияния заряженных частиц друг на друга, не учитываются их столкновения, то есть при расчете движения заряженных частиц рассматриваются только внешние электромагнитные поля, которые не зависят от потоков заряженных частиц.

Применительно к методу плазменного синтеза УНС в жидкой среде для описания процессов движения и взаимодействия частиц целесообразно использовать квантово-кинетические модели. Именно они позволяют описывать процессы зарождения и роста кластерных групп углерода формирующих УНС в плазме в большом диапазоне линейных размеров, а также получить более простые модели, например, по сравнению с шредингеровскими.

В рассматриваемой анизотропной плазме дугового разряда происходит одновременное движение и взаимодействие различных частиц (электронов, ионов углерода, катализатора, среды), зарождение и рост кластерных групп со связями С‒С, С = С, С = С‒С формирующих УНС на основе упругих и неупругих столкновений частиц,

Непосредственно на кинетику происходящих явлений в плазме влияют электромагнитные процессы, среда, катализатор. Происходит изменение конфигурации рабочей зоны, связанной с разрушением исходного графитового сырья и ростом депозита на основе процессов тепло и массообмена.

Поэтому для построения модели такой сложной задачи, можно применить кинетический подход, использующий систему уравнение Больцмана для каждого вида частиц плазмы, дополненная условием парных столкновений между частицами.

∂ f      ∂ f     q                ∂ f

+ 9 ^ - ^а ( ( e ₊ 1 9 в ]) 2 а =

∂ t     ∂ r   m      c      ∂ ϑ

α

∂ f α

∂ t

СТ

где f _а - функция распределения компонентов плазмы; а = е , с , h.s - тип частицы в плазме (е - электрон, с - углерод, h - газ пузыря, s - катализатор); r - координаты частиц; E - напряженность электрического поля; B - магнитная индукция; 9 - поле скоростей частиц; q _a , m _a - заряд и масса частицы.

Оператор столкновений в правой части уравнения (1) представляет собой сумму интегралов парных столкновений частиц друг с другом в виде:

= 2 Л ( f a fa-fa f )i 9 - 9 d ad#, (2) СТ k = e , c, h , s V

∂ f α ∂ t

где f , f ‘ - функции распределения частиц до столкновения и после столкновения; 9 , 9 -скорости частиц до и после столкновения; d a = 4 RR cos 3 d Q - дифференциальное эффективное поперечное сечение рассеяния частиц с радиусами R 1 и R 2 на телесный угол d Q; ; 3 - угол между вектором скорости сталкивающихся частиц и линией движения, V - объем области плазмы.

Интеграл столкновений (2) учитывает все компоненты плазмы, взаимодействующие друг с другом. Он дополняется условиями упругих и неупругих парных столкновений между частицами. При неупругом столкновении частиц углерода, происходит преобразование энергии, и создаются энергетические условия образования ковалентных связей С-С, С = С формирующих кластерные группы.

Для нахождения параметров электромагнитного поля уравнения Больцмана (1) необходимо дополнить системой уравнений Максвелла, описывающей самосогласованное электрическое поле.

Процессы при электродуговом синтезе УНС относятся к высокотемпературным технологическим процессам, при которых температура плазмы, нагрев и охлаждение электродов оказывают прямое влияние на качество продукта в целом [11-20]. Поэтому в основу модели теплообмена применительно для рассматриваемого процесса должна быть положена общая теория теплопроводности с определенными граничными условиями. Проведенный анализ процесса элек-тродугового синтеза УНТ позволил выделить основные способы передачи тепла в рассматриваемой системе в плазме - теплопроводность и конвекция, излучением можно пренебречь вследствие незначительного влияния на процесс. Использование уравнений теплопроводности Фурье с учетом подвижных границ позволяет выполнить расчет температурного поля и найти начальные скорости и энергии частиц.

Наличие огромного числа взаимодействующих и движущихся частиц в плазме, требует дополнительной разработки специальных эффективных численных методов обработки больших объемов данных с использованием параллельных вычислений, необходимых для расчетов параметров процессов такой математической модели.

Заключение

Нахождение рациональных технологических условий синтеза УНС в жидкой среде, позволяющих получать конечный продукт с заданными свойствами и максимальным выходом возможно на основе предварительного математического моделирования процесса.

Разработка математической модели с учетом значительного количества факторов, влияющих на синтез, является сложной ресурсоемкой задачей.

Рассмотренные в работе возможные методы описания процессов , происходящих в низкотемпературной плазме, позволили сделать вывод о целесообразности использования кинетического подхода для описания рассмотренного плазменного синтеза УНС в жидкой среде. Использование уравнения Больцмана для описания каждого вида компонента плазмы, с учетом парных упругих и неупругих взаимодействий между частицами, позволяет рассматривать процессы их движения и взаимодействия. Это позволяет прогнозировать образование в плазме кластерных групп со связями С-С, С = С формирующих пентагоны и гексагоны, которые образуют архитектуру УНС и определяют количественный выход синтезируемого продукта.

Для описания параметров электромагнитного поля дугового разряда в модели необходимо использовать уравнения Максвелла, описывающих самосогласованное поле.

Использование дополнительно уравнения теплопроводности Фурье с учетом подвижных границ системы катод-плазма-анод позволит выполнить расчет температурного поля рассматриваемого объекта и найти начальные скорости и энергии частиц.