Особенности применения многомерного тензорного анализа при исследовании сетей интегрального обслуживания

DOI:

Вопрос анализа нагрузки на сетях связи всегда вызывал повышенный интерес, особенно в последние годы [1-3]. Это вызвано тем, что на сетях общего пользования наряду с традиционными видами возрастают другие виды информации (факсимильная, передача данных, интернет, видеотелефония и другие), превращая их, фактически, в сети интегрального обслуживания [4].

В таких сетях в зависимости от нагрузки, от числа источников информации осуществляется выбор оборудования узла коммутации, учитываются его качественные и количественные характеристики и, безусловно, все затраты на установление и эксплуатацию.

Вопросам применения тензорной методологии для анализа сетей посвящено достаточно много работ. В частности, в работе [5] представлены результаты исследования тензорной модели многопутевой маршрутизации с обеспечением качества обслуживания в телекоммуникационных сетях. Работа [6] посвящена оптимизации цифровой сети интегрального обслуживания с конечным числом пользователей и блокировками. В [7] исследуются характеристики пакетных сетей узловым методом тензорного анализа. В работе [8] в качестве основного инвариантного уравнения при анализе нагрузки сети взята формула интенсивности нагрузки. В данной статье предлагается тензор, учитывающий стоимость узла коммутации 5. Если обобщить предлагаемые тензоры и использовать многомерный матричный подход, тогда можно записать

B=N-A                          (1)

В этом случае матрица B одновременно содержит данные матрицы интенсивности нагрузки Y и матрицы стоимости узла коммутации S; матрица A - данные удельной нагрузки у и удельной стоимости и; N - число источников узла коммутации.

ПОСТАНОВКА ЗАДАЧИ АНАЛИЗА

Рассмотрим особенности применения многомерного тензорного анализа к решению вопросов на сетях интегрального обслуживания на конкретном примере. Для постановки задачи возьмём сеть связи, состоящую из пятнадцати узлов.

Каждый коммутационный узел имеет соответствующие параметры:

• •    интенсивность нагрузки Y ;

• •    стоимость S узла коммутации;

• •    N - число источников узла коммутации;

• •    удельная нагрузка у одного источника информации;

• •    удельная стоимость и одного источника информации.

Необходимо найти соотношение между нагрузкой, числом абонентов и удельной нагрузкой, а также соотношение между суммарной стоимостью, числом источников и удельной стоимостью в сети для дальнейшего анализа с целью создания оптимальной топологии.

Задачу можно формулировать и иначе: при заданной топологии найти оптимальные распределения нагрузки для повышения эффективности работы в сети и одновременно предусмотреть затраты на оборудование узлов коммутации и самой сети.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Следуя методу Г. Крона [9-11], приведем более простую проекцию этой же 15-ти узловой сети, так как представленная в [8] проекция сложна для исследования. Согласно методу тензорного анализа, под пятнадцати узловой сетью понимается группа возможных комбинаций соединения узлов. Между различными проекциями существуют матрицы перехода. Поэтому можно получить решение для любой проекции, а затем с помощью известных формул перенести полученные результаты на другие проекции. При этом для получения результатов можно выбрать удобную (примитивную) проекцию, где меньше решений или они значительно проще.

Для такой проекции имеется решение, оно простое и может быть представлено в виде матриц для всей сети в целом.

i

где

Aijk

^Ai 1 k ⁼

y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 y 11 y 12 y 13 y 14 y 15

^Ai 2 k ⁼

u 1

u 2

u 3

u 4

u 5

u 6

u 7

u 8    ;

u 9

u 10

u 11

u 12

u 13

u 14

u 15

В , ijk

^Bi 1 k ⁼

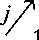
i ₄

=7

1 k

Y 1

Y 2

Y 3

Y 4

Y 5

Y 6

Y 7

Y 8

Y 9

Y 10

Y 11

Y 12

Y 13

Y 14

Y 15

B i 2 k =

S 1

S 2

S 3

S 4

S 5

S 6

S 7

S 8

S 9

S 10

S 11

S 12

S 13

S 14

S 15

Матрица для числа источников N будет иметь следующий вид:

	N 1	0	0	0	0	0	0	0	0	0	0	0	0	0	0
	0	N 2	0	0	0	0	0	0	0	0	0	0	0	0	0
	0	0	N 3	0	0	0	0	0	0	0	0	0	0	0	0
	0	0	0	N 4	0	0	0	0	0	0	0	0	0	0	0
	0	0	0	0	N 5	0	0	0	0	0	0	0	0	0	0
	0	0	0	0	0	N 6	0	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	N 7	0	0	0	0	0	0	0	0
N =	0	0	0	0	0	0	0	N 8	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	N 9	0	0	0	0	0	0
	0	0	0	0	0	0	0	0	0	N 10	0	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	N 11	0	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	N 12	0	0	0
	0	0	0	0	0	0	0	0	0	0	0	0	N 13	0	0
	0	0	0	0	0	0	0	0	0	0	0	0	0	N 14	0
	0	0	0	0	0	0	0	0	0	0	0	0	0	0	N 15

При этом сохраняются основные соотношения:

Y = N -у и S = N • u.

Косвенное влияние между узлами коммутации отсутствует, поэтому в данном примере все недиагональные элементы матрицы N равны нулю.

Тогда можно перейти к решению первоначальной проекции. Достаточно найти матрицу перехода. Для этого в исследуемой сети задаются новые удельные интенсивности и удельные стоимости, число которых равно числу контуров в сети.

Если обратиться, к примеру, рассмотренному в предыдущей статье [12], то становится понятно, что соотношения между удельными интенсивностями и, соответственно, удельными стоимостями различных сетей идентичны.

Таким образом, можно считать, что матрица перехода одна, но применима она будет к разным удельным характеристикам.

Тогда, пользуясь операцией умножения многомерных матриц, переходим к контурам исходной системы:

101 1

- 1

B' = С_т . в =

0 100000

1 0 10000

0 -1 -11110

0   0   0   0  1   1

		" Y1	S 1
		Y 2	S 2
		Y 3	S 3
		Y4	S 4
		Y 5	S 5
0		Y 6	S 6
0		Y7	S 7
0	X	Y8	S 8
0		Y 9	S 9
1		Y 0	S 10
		Y 1	S 11
		Y .	S 12
		Y 3	S 13
		Y 14	S 14
		_ Y 15	S 15

1 ⁺ 3 ⁺ 4 ⁺ 6

Y^ - Y 4 + Y 5 + Y 7

- Y 6 - Y 7 + Y 8 + Y 9 + Y 0

Y 9 ⁺ Y 0 - ^Y 11 ⁺ Y 2 ⁺ Y 3

Y^ + Y 3 + Y 4 + Y 5

S 1 + S 3 + S 4 + S 6

S 2

- S 4 + S 5

+ S

- S ₆ - S ₇ + S ₈ + S ₉ + S ₁₀

S 9 + S _w - S _n + S 12 + S 13

S 12 + S 13 + S 14 + S 15

На рисунке 1 представлена структурная модель трехмерной матрицы В :

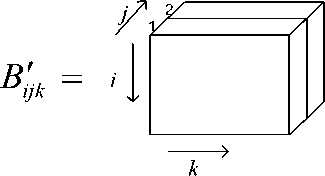
Рисунок 1. Структурная модель матрицы В .

Figure 1. Structural model of matrix В ' .

где

Y ' = 1 IBAkll

Y i + Y 3 + Y 4 + Y,

Y - Y4 + Y5 + Y7

- Y - Y 7 + Y + Y 9 + Y o

Y 9 + Y o - Y i + Y 12 + Y 3

Y 2 + Y 3 + Y 14 + Y 5

;

B 1 + B 3 + B 4 + B ₆

B2 - B4 + B + B7

B ' = 1 I B A J1 =

- B 6 - B 7 + B 8 + B 9 + B io

B ₉ + B io - B ii + B 12 + B 13

B i2 + B i3 + B i4 + B i ₅

Матрица числа источников в контурах исходной системы, имеем вид:

	N =CT-N -C =
N 1 + N 3 + N 4 + N 6 - N 4 - N 6 0	- N 4                 - N 6                     o                   o N + N + N + N       - N              o              o - N 7        N 6 + N 7 + N 8 + N 9 + Nw        N 9 + Nш                 o o                 N 9 + Nw        N 9 + N w + N u + N 12 + N ,3        N 12 + N ,3
0	o                     o                      N 12 + N .3           N 12 + N .3 + N |4 + N .5

Согласно постулату второго обобщения, уравнение состояния исходной сети, записанное в матричной форме, имеет тот же вид, что и уравнение состояния простейшей сети, то есть:

B' = N' "Л'.                                           (2)

Эквивалентная система уравнений состояния исходной сети:

• •    для интенсивности нагрузки

^Y i ^{+ Y} 3 ^{+ Y} 4 ^{+ Y} 6 = ^{( N} i ^{+ N} 3 ^{+ N} 4 ^{+ N} 6 ) "  y a - ^N 4 ’ y b - ^N 6 "  y c

^Y 2 - ^Y 4 ^{+ Y} 5 ^{+ Y} 7 = ^{- N} 4 • y a ^{+ ( N} 2 ^{+ N} 4 ^{+ N} 5 ^{+ N} ? ) ‘ y b - ^N 7 ’ y c

< -Y6 - Y7 + Y8 + Y9 + Yo = -N6 • ya - N7 • yb + (N6 + N7 + N8 + N9 + Nio ) • yc + (N9 + Ni0 ) • yd

Y9 + Yo - Yii + Yi2 + 1^3 = (N9 + Nio) • Ус + (N9 + Nio + Nii + Ni2 + Ni3) • yd + (Ni2 + Ni3) • Уе

^Y i2 ⁺ Y i3 ^{+ Y} i4 ⁺ Y i5 = ^{( N} i2 ^{+ N} i3 ) • y d ^{+ ( N} i2 ^{+ N} i3 ^{+ N} i4 ^{+ N} i5 ) "  y e

• •    для стоимости узла коммутации

S1 + S3 + S4 + S6 - (N1 + N3 + N4 + N6) • ua — N4 • ub — N6 • uc

S2 — S4 + S5 + S7 — — N4 • ua + (N2 + N4 + N5 + N7) • Ub — N7 • uc

’ - ^S 6 - ^S 7 ^{+ S} 8 ^{+ S} 9 ^{+ S} 10 ^— - ^N 6 • u a - ^N 7 * u b ^{+ ( N} 6 ^{+ N} 7 ^{+ N} 8 ^{+ N} 9 ^{+ N} 10 ) * u c ^{+ ( N} 9 ^{+ N} 10 ) * ^U d

S9 + S1o — S11 + S12 + S13 — (N9 + N1o) • uc + (N9 + N1o + Nn + N12 + N13) • ud + (N12 + N(3) • ue

_ S12 + S13 + S14 + S15 — (N12 + N13) • Ud + (N12 + N13 + N14 + N15) • ue

В итоге получаем системы из пяти уравнений и пяти неизвестных. Решение таких систем не представляет большого труда.

Таким образом, тензорный метод позволяет проводить многомерный анализ сетей интегрального обслуживания. Все результаты содержатся в одной трехмерной матрице, которая представляет собой «хранилище» данных.

Можно легко рассмотреть и извлечь данные из многомерной структуры в применении к собственным задачам (рисунок 2).

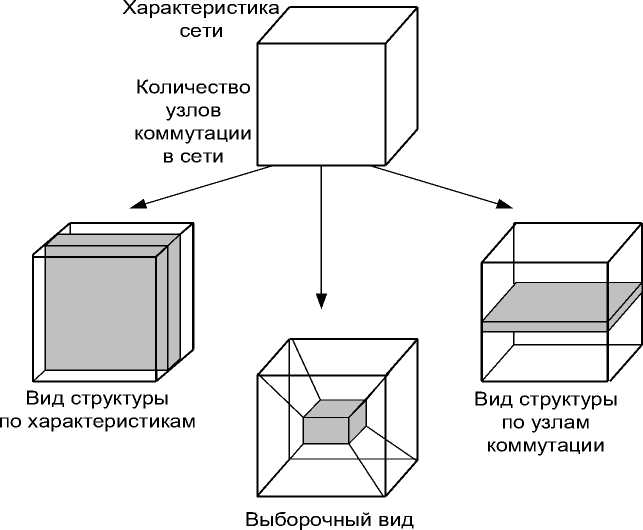
Рисунок 2. Структурная модель многомерной матрицы.

Figure 2. Structural model of a multidimensional matrix.

Использование многомерного тензорного анализа позволяет производить анализ одновременно по нескольким характеристикам, а также синтезировать структуру сети интегрального обслуживания по нескольким критериям одновременно.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе рассмотрены особенности применения тензорного анализа при исследовании сетей интегрального обслуживания и разработан оригинальный метод многомерного тензорного анализа сетей интегрального обслуживания. Для представленной постановки задачи выведены и обоснованы основные соотношения для расчета. Отметим, что разработанный метод многомерного тензорного анализа применим для анализа сетей с интеграцией служб на основе диакоптики. Особенности применения метода многомерного тензорного анализа отражены в приведенных примерах расчетов и полученных результатах на конкретных топологиях сетей. Подтверждено, что многомерный тензорный метод позволяет анализировать сети интегрального обслуживания одновременно по нескольким характеристикам. Более того, на основе многомерного тензорного анализа можно осуществлять синтез структуры сети по заранее заданным характеристикам.