Особенности развития математических способностей

На сегодняшний день уровень требований к освоению математических знаний у выпускников школ очень высок. Технические ВУЗы открывают свои двери в первую очередь для одаренных детей, которые обладают знаниями на порядок выше, чем школьная программа. В отечественной и зарубежной науке широко разработаны и теоретически описаны природа и особенности интеллекта одаренных детей. Старшеклассники, занимающиеся по углубленной программе математики, чаще имеют более высокий уровень интеллекта, чем дети осваивающие стандартный курс. Определяя интеллект в наиболее общем виде мы определяем его как систему всех (когнитивных) способностей индивида: это ощущение, восприятие, память, представления, мышление, воображение (Мещерякова, Зинченко). В изучение интеллекта можно выделить две основных концепции: одна основана на представлении о наличии одного общего фактора интеллекта, представленного на всех уровнях интеллектуального функционирования (Спирмен, Кеттелл, Вернон и др.), вторая на наличии множества независимых интеллектуальных способностей (Терстоун, Гилфорд, Гарднер). В отечественной науке также разрабатывались теории интеллекта, их часто называют экспериментальнопсихологическими. Особенностями интеллектуального развития в юношеском возрасте являются: переход к формально- образному мышлению, появление способности к рефлексии и самоанализу, развитие специальных способностей, формирование собственного стиля интеллектуальной деятельности.

Выявление математически одаренных школьников происходит достаточно стандартно. В первую очередь это общая успеваемость по предметам, причем срез успеваемости может быть как по всем школьным предметам, так и только по профильным. Сюда же можно отнести скорость и способность успешно усваивать материалы повышенной сложности. Во вторую очередь это успехи отдельных учеников на олимпиадах различного уровня. То есть, высокие достижения учеников являются конечным и определяющим одаренность результатами. Внешние и очевидные показатели одаренности это результативность и успешность, мы определяем как первый блок. Второй, процессуальный блок раскрывает особенности механизмов мыслительных процессов при решении задач повышенной сложности. Познавательная деятельность на этом уровне характеризуется оригинальностью путей решения задач, выбором методов позволяющих найти оптимальный путь решения задачи [1]. Многие ученые сходятся во мнении, что успешность в решении математических задач опирается именно на методы и приемы математического мышления, чем на знания какого-то конкретного учебного материала и отдельных фактов.

Наша исследовательская задача заключается в исследовании способности интеллекта детей изучающих углубленный курс математики синтезировать и предлагать нескольких методов решения. Рассмотрим пример мыслительного процесса решения задачи обучающегося в профильной математической школе. Процесс восприятия задачи осуществляется на первом этапе через способность к формализованному восприятию, то есть понимание формальной структуры задачи. Наше внимание захватывает второй этап, когда задействованы уже несколько интеллектуальных способностей.

Примером будет служить часто встречающаяся в математике задача о нахождении какой-нибудь части треугольника или другой произвольной фигуры на плоскости либо анализ взаимоположения прямых в пространстве. Например, поиск площади треугольника основными методами привычными нам всем: площадь как произведение высоты треугольника на половину его основания либо по формуле Герона. Решение задачи начинается с рассмотрения различных ситуаций и поиска оптимально быстрого решения. Вспомним базовые формулировки и уравнения аналитической геометрии на поверхности и пространства.

В данном случае, было предложено решить эту задачу введя систему координат и вычислять все искомые нами величины.

~Под системой координат на плоскости понимают способ,позволяющий численно описать положение точки плоскости, одной из таких является декарто-ва(прямоугольная) система координат.

~Координатами точки A в системе координат Oxy (Oij) называются координаты радиус-вектора OM. Если OM=(x; y), число x называется абсциссой точки А, а y -ординатой точки А.

~Расстояние между двумя точками:

d=V(x2 - xl)2 + (у 2 - yl)5

~Деление отрезка в данном отношении:

Отрезок AB, такой, что A(x1; y1) и

B(x2; y2) и они делятся в отношении λ, т. е.

AM= λ*MB тогда координаты точки M будут

A'l 4- Л ♦ a 2 yl -f- Л ♦ y2

M( 1 + Л :  1+Л  )

~

Пожалуй, одно из самых полезных свойств метода координат это формула для нахождения площади треугольника.

Задача.

Требуется найти площадь треугольника

ABC с вершинами A(x 1 ; y 1 ), B(x 2 ; y 3 ), C(x 3 ; y 3 ).

Решение: отпустим из вершин A, B, C перпендикуляры AA 1, BB 1, CC 1 на ось Ox (см. рисунок). Очевидно, что

S ABC = S AABB + S CCBB -S AACC . Поэтому

S ABC                                 =

0'1 + y2)(x2 - xl) (y2 4- уЗХхЗ - x2) 0'1 + уЗХхЗ - xl)

2        +        2                  2

(*)

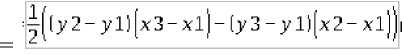
При вычислении значения площади мы могли получить отрицательное или нулевое значение. Первое следует взять в модуль, а второе означает, что данные точки лежат на одной прямой.

Доказательство справедливости формулы площади треугольника можно было осуществить рассуждая не через координаты, а через векторы.

Векторным произведением вектора a на вектор b называется вектор c, который:

• 1)    перпендикулярен векторам a и b, т.е. a ┴c и c ┴b;

• 2)    имеет длину численно равную площади параллелограмма, построенного на векторах a и b как на сторонах, т.е.

  

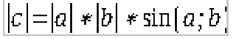
Заметим, что значение площади параллелограмма в два раза больше площади треугольника (параллелограмм построен на двух сторонах и угле между ними), та- ким образом 1/2|с| численно равно площади треугольника (*).

Для более простого, удобного применения можно записать площадь треугольни- ка, как определитель матрицы.

Таким образом, способность продуцировать оригинальные решения задач повышенной сложности является важнейшей характеристикой мышления. Развитие этой способности влияет на формирование системного мышления, возможности оперировать более сложным материалом [2]. Во время решения задач актуализируются когнитивные процессы, идет как процесс их проявления так и развития. Данная способность не является критерием отбора или выделения одаренных детей, но является их отличительной чертой. Можно предположить, что данная черта связана, с одной стороны, с природными способностями и задатками, а с другой стороны со стимулированием интеллектуально развития за счет обучение и тренировки. Участие в олимпиадах предполагает серьезную подготовку к ним, что способствует развитию интеллекта и расширению обще- го кругозора школьников.