Отказоустойчивая статическая оперативная память на основе ячеек БМК

Введение Известно, что минимизация логических (переключательных) функций выполняется в Булевом базисе И, ИЛИ, НЕ [1, 2]. Пусть задана некоторая бинарная переключательная функция своей таблицей истинности (рис. 1). a     Ь     с      f (abc) ООО  0 0     0     1        0 0  10   0 0  11   1 10  0   0 10  1   1 110  1 111  1 Рис. 1. Таблица истинности некоторой бинарной переключательной функции Минимизация в булевом базисе И, ИЛИ, НЕ, например по карте Карно (рис. 2), позволяет получить выражение f(abc) = ab v ac v bc,         (1) © Тюрин С. Ф., Прохоров А. С., 2016

которое представляет собой так называемую мажоритарную функцию. c 1-------------------------------------< b 1----------------------------------------------------------------------------1 0  13  2 0    о  ^  0 4      5      I 7       6 о  Д Ж i ac bc ab Рис. 2. Минимизация в булевом базисе И, ИЛИ, НЕ функции рис. 1 по карте Карно В выражении (1) имеется три импли-канты, но ни количество импликант, ни число переменных в импликанте при минимизации в булевом базисе не ограничено. То есть, такое представление функции является своего рода линейным (рис. 3).

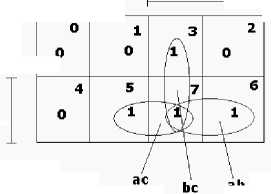
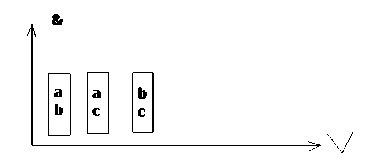
Рис. 3. Линейное представление функции в булевом базисе

После чего полученные выражения представляются в заданном базисе [3, 4]. Возникают некоторые сомнения об оптимальности полученных за два "приема" схем. Тем более, что в случае минимизации в заданном базисе, например ИНЕ, ИЛИ-НЕ, можно было бы сразу получать схему, совместив по возможности процесс её построения с процессом нахождения импликант, т. е. выполнять преобразования за один этап. Однако известно, что минимизация в произвольных базисах крайне сложна, что вызвано лавинообразно увеличивающейся комбинаторной сложностью задачи [5–8].

В [1–12] предложена концепция функционально-полного толерантного (ФПТ) логического базиса и элемента. ФПТ-элемент сохраняет свойство базисности в смысле теоремы Поста при заданной модели отказов. ФПТ-базис также предпочтителен для реализации широкого класса логических (булевых) функций по сравнению с традиционными базисами И-НЕ, ИЛИ-НЕ.

• 2.    Минимизация логической функции в базисе (X 1 v Х 2 )

Как же минимизировать функцию рис. 1 в базисе только одной функции, например 2И-НЕ

(x i v X 2 ).                    (2)

В этом случае ограничено число дизъюнкций с инверсией не более чем одной переменной – до двух. То есть, представление функции не линейное, а древовидное, первые два яруса имеют вид (рис. 4).

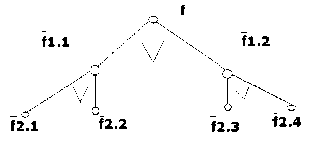
Рис. 4. Древовидное (два уровня) представление – корнем вверх – функции в базисе И-НЕ (xi v X2)

Следует заметить, что если бы базис был не 2И-НЕ, а 3И-НЕ, то дерево (рис. 4) было бы не бинарное, а тернарное.

Продолжаем, дл я третьего уровня:

^f = ^f1 ^{V f} 3.2 ^{V f} 3.3 ^{V f} 3 .4 ^{V f} 3.5 ^{V f} 3.6 ^{V f} 3.7 ^{V f} 3.8 .   ⁽³⁾

Необходимо определить все подфункции этого уровня. То есть, найти минимальное дерево из всех возможных деревьев!

• 3.    Проверка покрытия заданной

функции одним элементом (x i v X 2 )

Будем получать всевозможные выражения вида

(f ij V f_{4 +} i );f e {a,b,c,0,1},        (4)

т.е. вначале из переменных f(abc) констант 0, 1 и строить соответствующие дополнительные столбцы таблицы истинности – получим рис. 5.

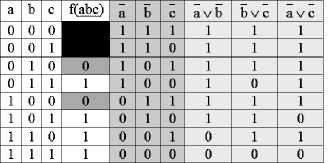
Рис. 5. Расширенная таблица истинности функции, представленной рис. 1 для выражений вида (5)

(f _L i v M;f e {a,b,c,0,1}.    (5)

Ни в одном дополнительном столбце (рис. 5) единицы не соответствуют единицам функции f(abc). То есть, одним элементом заданную функцию не реализовать. Кроме того, ни один дополнительный столбец (рис. 5) не имплицирует f(abc).

• 4.    Проверка возможности реализации з а данной функции двумя элементами

(x i V X 2 )

Полагаем, в первую очередь необходимо проверить, не покрываются ли единицы функции ее переменными и дизъюнкциями двух таких конъюнкций. Для этого требуется 2 элемента, что можно назвать "простым" или "примитивным" представлением, так как некоторые элементы используются как простые инверторы. То есть, иными словами,

(f i.1 ∨ f i.2 );f ∈ {a, b, c,0,1, a, b, c}.      (6)

Получим рис. 6.

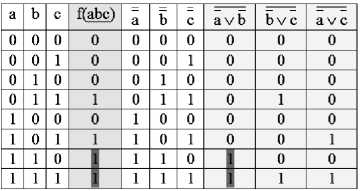
Рис. 6. Проверка " простых " покрытий, реализуемых двумя элементами

(x 1 ∨ x 2 )

Ни один столбец рис. 6 не покрывает своими единицами единиц функции f(abc). Таким образом, двумя элементами (когда один – общий инвертор) заданную фу нкцию реали зо вать невозможно. Но столбцы a ∨ b , b ∨ c , a ∨ c – импликанты f(abc)! Они покрывают все единицы f(abc) и совершенно равноценны – каждый покрывает две единицы из четырех, но двумя столбцами не обойтись. Лег ко, од на ко, в и деть, что дизъюнкция столбцов a ∨ b , b ∨ c , a ∨ c покрывает единицы функции, но в том-то и дело, что ее нельзя использовать в нашем сл учае!

Выберем первый столбец a ∨ b , ибо он допустим, и попробуем определить покрытие в нашем базисе дл я оставшихся едини ц:

f = a ∨ b ∨ f ∨ f ∨ f ∨ f . (7)

3.5 3.6 3.7 3.8

То есть необходимы уже два элемента с базисом (x 1 ∨ x 2 ) и теперь следует допус ти мым образом комбинировать столбцы b ∨ c , a ∨ c . Как комбинировать? Все тем же способом

f ∨ f ∨ f ∨ f , (8)

3.5 3.6 3 .7 3.8

так как "левое плечо" (x 1 ∨ x 2 ) уже занято, теперь необходимо получить выражение под "правой" инверсией (рис. 7).

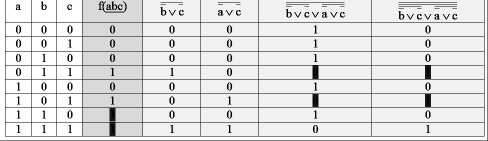
Рис. 7. Проверка покрытий, реализуемых комбинированием                 b ∨ c , a ∨ c , b ∨ c ∨ a ∨ c. (9)

Видно, что простая инверсия столбца b∨c∨a∨c приведет к получению требуемого покрытия. Таким образом, выражение b ∨ c ∨ a ∨ c           (10)

также является импликантой и совместно с a ∨ b покрывает все единицы функции f(abc). Это не что иное, как еще 4 элемента. Итак, получили 6 элементов (24 транзистора):

a ∨ b ∨ b ∨ c ∨ a ∨ c

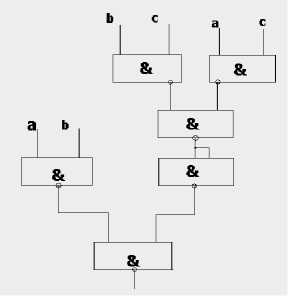
Рис. 8. Схема реализации мажоритарной функции в базисе 2И-НЕ

По существу, рис. 8 – это дерево корнем вниз. Имеется 4 уровня, на каждом уровне реализуется функция (x 1 ∨ x 2 ) . Быстродействие такой схемы -4 τ , где τ – задержка одного элемента 2И-НЕ (4 транзистора).

Таким образом, минимизация в базисе (x 1 ∨ x 2 ) сводится к нахождению всех им-пликант вида:

(f i.1 ∨ f i.2 );f ∈ {a,b,c,0,1, a,b,c,f j ,f j },(12) т. е. построенных из переменных, их инверсий, констант и уже полученных импликант. При этом решается задача оптимального покрытия импликантами единичных наборов функции.

• 5.    Минимизация логической

функции в базисе (x 1 ∨ x 2 )(x 3 ∨ x 4 )

Возникает вопрос: как же минимизировать функцию рис. 1 в избыточном базисе? Например:

(x 1 ∨ x 2 )(x 3 ∨ x 4 ).          (13)

В этом случае ограничено число конъюнкций до двух, число переменных в конъ- юнкции также не более двух, да еще обязательна инверсия! Искомое выражение представляет собой не ДНФ, а вложенные друг в друга выражения вида

(f i.1 ∨ f i.2 )(f i.3 ∨ f i.4 ).              (14)

То есть представление функции также древовидное, но "дерево" уже другое (рис. 5).

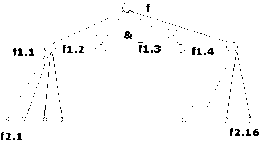
Рис. 9. Древовидное представление функции в базисе (x1 ∨ x2)(x3 ∨ x4)

На рис. 9 индекс подфункции fi.j.k.m                  (15)

указывает ярус дерева (i), позицию (j, =1…4), верхний ярус (k), к какой позиции верхнего яруса подключается (m), причем i ≠ k. В таком представлении пара соседних листов объединяется конъюнкцией, между двумя крайними парами – дизъюнкция, а в вершине – инверсия, из которой исходят эти пары.

• 6.    Проверка покрытия заданной функции одним элементом

(x 1 ∨ x 2 )(x 3 ∨ x 4 )

Нам необходимо получить всевозможные выражения вида

(f i.1 ∨ f i.2 )(f i.3 ∨ f i.4 );f ∈ {a,b,c,0,1}, (16)

т.е. вначале из переменных f(abc) констант 0, 1 и строить соответствующие дополнительные столбцы таблицы истинности (рис. 10).

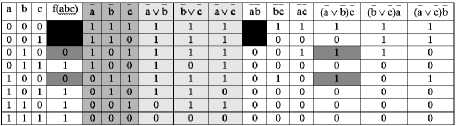
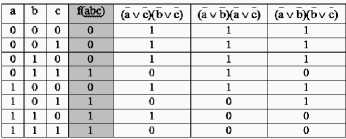
Рис. 10. Расширенная таблица истинности функции, представленной рис. 1 для выражений вида

(f i.1 ∨ f i.2 )(f i.3 ∨ f i.4 );f ∈ {a,b,c,0,1}

Ни один столбец рис. 10 не покрывает своими единицами единиц функции f(abc). То есть, одним элементом заданную функцию не реализовать.

• 7.    Проверка возможности реализации заданной функции двумя элементами (x 1 ∨ x 2 )(x 3 ∨ x 4 )

В целом, следует проверить, не покрываются ли единицы функции ее переменными, конъюнкциями этих переменных длиной 2 и дизъюнкциями двух таких конъюнкций – для этого требуется 2 элемента. Это можно назвать "простым" или "примитивным" представлением (рис. 11).

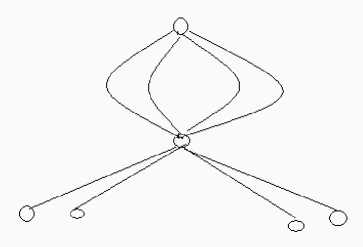
Рис. 11. " Простое " или " примитивное " представление некоторой функции из двух элементов (x 1 ∨ x 2 )(x 3 ∨ x 4 ) , один из которых используется как инвертор

Получим рис. 12.

a b с ООО О 0 1	W - О     О О     О	ь О О	с   avb bvc ООО 1 0 0	a v с 0 0	ab     ас 0     0 0        1		Ьс 0 1
О 1 О	О     О	1	ООО	0		0	1
О 1 1 1 О О	1       О О      1	1 О	1       0       1 ООО	0 0		1 1	1 0
1 0 1	1         1	О	1      О      О	1		1	1
1 1 О 1 1 1	1         1 1         1	1 1	0      1       0 1           1            1	0 1		1 1	1 1

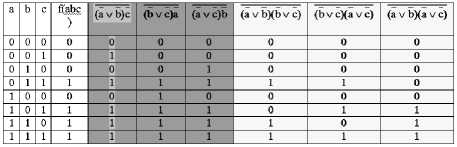
Рис.12. Проверка " простых " покрытий, реализуемых двумя элементами (x 1 ∨ x 2 )(x 3 ∨ x 4 )

Ни один столбец рис. 12 не покрывает своими единицами единиц функции f(abc).

Таким образом, двумя элементами (когда один – общий инвертор) заданную функцию реализовать невозможно.

Лег ко, од на ко, в и деть, что дизъюнкция столбцов a ∨ b , b ∨ c , a ∨ c покрывает единицы функции, но к сожалению, ее нельзя использовать в нашем случае! Здесь мы пока не использовали возможность инверсий некоторых или всех входных переменных, т.е. строго говоря, это должно выглядеть следующим образом:

(f i.1 ∨ f i.2 )(f i.3 ∨ f i.4 );f ∈ {a,b,c,0,1,a,b,c}.(17) Полагаем, необходимо рис. 10, 12 еще дополнить всеми вариантами использования инверсий переменных.

• 8.    Проверка возможности реализации заданной функции тремя элементами (x 1 ∨ x 2 )(x 3 ∨ x 4 )

Теперь следует комбинировать столбцы, т.е. получать выражения вида (f j.1 ∨ f j.2 )(f j.3 ∨ f j.4 ) из полученных ранее столбцов вида

(f i.1 ∨ f i.2 )(f i.3 ∨ f i.4 );f ∈ {a,b,c,0,1,a, b, c}. (18)

Ле гко увидеть, что конъюнкция ab и (a ∨ b)c покрывает все единицы f(abc).

Значит, можно реализовать ее в виде (ab)(a ∨ b)(c) всего тремя элементами! (рис.13):

В каждом элементе (x 1 ∨ x 2 )(x 3 ∨ x 4 ) восемь транзисторов [9, 10], итого 24 транзистора, как и в схеме рис. 6, однако быстродействие в количестве элементов - 2 τ ’, где τ ’ – быстродействие одного элемента с базисом (x 1 ∨ x 2 )(x 3 ∨ x 4 ) , в котором сигнал проходит 2 транзистора, итого быстродействие – 4 транзистора, а в схеме рис. 6 – 8 транзисторов.

Дело в том, что в схемах с базисом (x 1 ∨ x 2 )(x 3 ∨ x 4 ) [11] цепи подключения + и общей шины одинаковы и содержат 2 последовательных транзистора n -МОП, p -МОП, а в элементах с базисом (x 1 ∨ x 2 ) имеется один n -МОП транзистор, но два последовательных p -МОП.

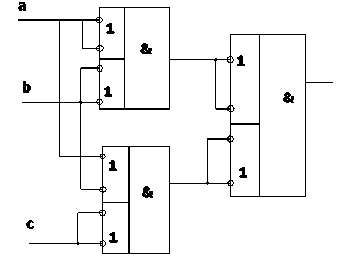
Рис. 13. Реализация f(abc) = (ab)(a ∨ b)(c) тремя элементами с базисом (x 1 ∨ x 2 )(x 3 ∨ x 4 )

Заключение

Таким образом, оптимальное покрытие логических функций в традиционном базисе (x 1 ∨ x 2 ) и в избыточном базисе (x 1 ∨ x 2 )(x 3 ∨ x 4 ) в отличие от " линейного " булева базиса И, ИЛИ, НЕ может быть найдено только в виде дерева соответствующих им-пликант. Построение всевозможных различных допустимых для данного базиса импли-кант, а также минимизация соответствующих деревьев представляет собой сложную комбинаторную задачу. Оптимальная реализация мажоритарной функции в избыточном базисе (x 1 ∨ x 2 )(x 3 ∨ x 4 ) равноценна реализации в базисе (x 1 ∨ x 2 ) по числу транзисторов, но предпочтительна по быстродействию. Целесообразна автоматизация поиска оптимального покрытия.