Отпуск мартенсита в ходе быстрого нагрева

Рассматривается стадия двухфазного распада мартенсита при отпуске. Обозначим через Р долю распавшегося мартенсита P = V*/V , где V0 - исходный, а V* - превращенный объем. Для изотермических условий распада Курдюмов и Лысак [3, 4] установили закон распада:

dP = v • n-(1 - P) dT,(1)

где n – число карбидных зародышей в единице объема, v – средний объем одной превращенной области, T - длительность распада при температуре T . Множитель v • n подчиняется соотношению Аррениусова типа:

v • n = A0e-E /RT.(2)

Если распад идет в условиях непрерывного нагрева со скоростью V H , то d T = dT / V H , причем скорость нагрева V_H будем считать постоянной. Тогда из (1), (2) имеем:

dP/(1 - P) = A0e-E/RTdT/ VH .(3)

Пусть при нагреве от 0 К до требуемой температуры T1 доля распада составляет P1 . Тогда выполняется соотношение:

P1

ITTP^ = (A»/Vh ) I Ao e -E / RTdT *(4)

0 (1 P)

Интеграл в левой части (4) – табличный, соответственно получаем:

T 1

- ln(1 - P) = (Ao / Vh ) I Aoe-E / RTdT.(5)

В правом интеграле вводим новую переменную:

Краткие сообщения

E

RT

E dT =----- dx ,

R • x ²

и приводим его к виду:

.     - - / RT i

- ln(1 - P ) = A^ - [ -1 e^xdx .

¹ V R      x ²

H —TO

Согласно таблицам интегралов [5]:

f *. exdx =—— + Ei( x), x2         x где Ei(x) - интегральная показательная функция. По данным [3, 4] величина Е порядка 130 кДж/моль, поэтому ниже Ac 1 отношение -RT1 > 10 . При таких значениях аргумента можно использовать асимптотический ряд [6]:

e ^— a (

Ei(-a) = -—I 1 a к

1 2! 3!

^— a⁺a ²

--- • •

a ³

.

Тогда с хорошей точностью имеем:

E / RT ₁

f -2 exdx = x2

—TO

_e — - / RT i

( - / RT 1 ) 2

i—

2!

к

( - / RT 1 ) ⁺ ( - / RT 1 )²

3!

• • •

( - / RT 1 )³ ,

.

Ограничиваясь первыми двумя членами ряда, найдем:

— in(i — р ) ₌ A L RT 1L e^- / RT i ¹   V H E

.

Теперь легко определить искомую скорость, нагрев с которой создаст долю распада не превосходящую некоторого критического значения P _кр :

VH =

A     ^RT i2 e - - / RT 1

ln(1 — Р кр ) -

.

При малых критических долях ln ( 1 — Р _кр ) = — Р _кр , тогда соотношение (8) упрощается:

VH =

A 0 RT 1 ²

Pкр E

e — - / RT 1

На рисунке приведен график зависимости V_H = f ( T 1 ) для Р_кр = 0,01, рассчитанный по формуле (9). Если это условие «ослабить», например, принять степень распада равной 0,1 или 0,2, то скорости нагрева, определенные по графику, нужно уменьшить в 10 и 20 раз соответственно. При расчете приняты следующие значения величин (согласно [2]): А 0 = 0,7∙10¹⁹ мин^–1, Е = 33 ккал/моль, R = 8,31 Дж/моль∙град.

Модель Еднерала–Скакова

Указанные авторы [5] нашли, что кинетический закон отпуска мартенсита ближе к уравнению Аврами, чем Лысака–Курдюмова, т.е. приняли

1 — e ^{ТТ о} ) ” | ,                                           (10)

P = рто где Pто - максимальная доля распада, т - время, т0 - кинетический параметр, определяемый соотношением:

— = B • e~^Q/RT ,                                      (11)

^Т 0

а m – параметр, который, вероятно, зависит от структурного состояния, наличия сильных карбидообразующих элементов и др.

В изотермических условиях:

m 1              Im dP = p- L--m. e --) dT.

m

^T 0

Если положить, как и ранее, что в условиях нагрева d r = dT/V H , то несложно получить дифференциальное уравнение:

_____dP _____= ^m "  B e- Q ■ m RT T m - 1 dT P ^- ( 1 - p/p ^- ) V m                "

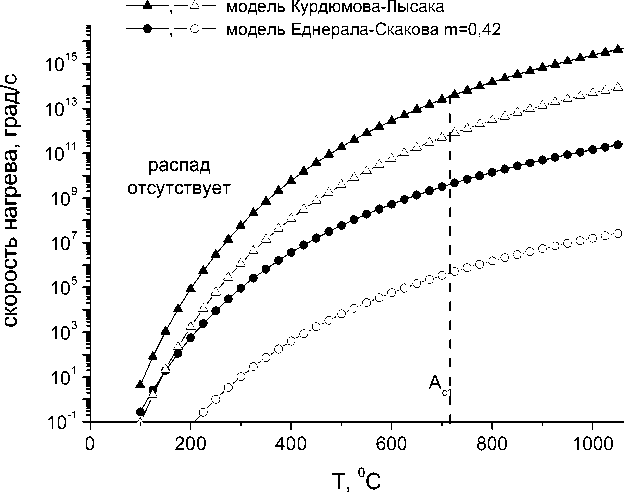
Зависимость скорости нагрева V H от температуры согласно теории Курдюмова–Лысака и Еднерала–Скакова, закрашенные символы соответствуют критической степени распада P кр = 0,01, а пустые P кр = 0,1

Интегрируя, найдем:

- In ( 1 - p/p ^- ) =

m. B m VH

m T 1

— J e~QmRT T m ^{- 1} dT .

(13а)

Введем новую переменную

x = - mQ;

RT

Преобразуем интеграл (13а) к виду:

dT =

mQ _{dx .}

R " x ²

- In (1 - p/p- ) = ( I)

m - 1 mB m

m VH

m mQ | R )

"

mQ RTl 1      1

e ^x dx .

J        x m + 1

-—

Для расчета интеграла в (14) используем формулу exe ex xk ,

т dx = k\—;-—dx +

J x k        J x k + 1

которую будем последовательно использовать для возникающих интегралов: xx    xx

[ -^-dx =    + ( m + 1 ) - e ^ + ( m + 1 )( m + 2 ) - e - +

J _vm + 1        _vm + 1 '       ' m+ +2 '      ' '        ' mm + 3

xx xx

xx ee + (m + 1)( m + 2)(m + 3) xm+4 + (m + 1)( m + 2)( m + 3)( m + 4) J -m^4

dx .

Поскольку верхний предел в (14) mQ]RT 1 >>  1, то полученный ряд дает асимптотическое разложение. Ограничиваясь тремя первыми членами указанного разложения

Краткие сообщения

- mQ/RT

∫

—TO

ex xm+1

dx = (—1)

m + 1 e - mQRT¹ — mQ/RT ( mQ/RT 1 ) m ^{+ 1}

₁ ⁽ m + ^{1 )} mQ RT ₁

( m + 1 )( m + 2 ) ( mQ/RT 1 ) 2

и, обозначая функцию, заданную в виде ряда в квадратных скобках, как F ( mQ/RT ₁ ) , получим:

о m ( ™ Л²      „— mQ/RT

— In(1 — pJp Ч =---1 mQ | • T • e--F{mQ/RT ).

• ¹¹ V VS ( R ) ¹ mQ/RT   ^{V U}

  Используя для расчета значения, взятые из данных работы [5], m = 0,42, B = 1,47-10¹⁰ сек, Q = 24 ккал/моль, видим, что отношение mQ/RT = 5071/ T₁ >  4, поэтому можно приближенно принять F ( mQ/RT ) = 1. Учитывая, что при малых Р ₁ можно полагать — ln ( 1 — P ₁ / p “ ) = P ₁ / p “ , а

• также учитывая, что по Лысаку P” = 0,7, окончательно получаем выражение для скорости на-
• грева:

B                 — Q/RT _       ^0,63 ^ ¹⁰¹ 0        — 240000/ T^

V H =------------------- T r e    ¹ =----------------4чт е T i

( ( PjP “ ) • ( Q/RT₁ ) )^Z m               ( P 1 ( 24000/ RT 1 ) ) ,

Результаты расчета V H по модели Еднерала–Скакова также приведены на рисунке. Конечно, между двумя кривыми на рисунке очень большие расхождения. Однако нам представляется, что данные Еднерала–Скакова более надежны, поскольку они получены с использованием метода электросопротивления, что значительно точнее, нежели анализ полуширины мартенситного дублета.

Данные рисунка отчетливо свидетельствуют о следующем: 1) для того, чтобы подавить двухфазный отпуск мартенсита углеродистых сталей при быстром нагреве до и выше критической температуры А1 (начало образования гамма-фазы) необходимы скорости нагрева от 1012 K/c (m = 0,42) по теории Еднерала–Скакова до 5∙1013 К/c по теории Лысака–Курдюмова. Такие скорости нагрева вряд ли можно реализовать на современном этапе развития техники; 2) при умень- шении скорости нагрева, по отношению к указанным значениям, степень отпуска возрастает. Тем не менее для того, чтобы произошел полураспад мартенсита нужны скорости выше 6∙109 и 6∙105 К/c соответственно каждой из рассмотренных моделей. В отношении легированных сталей необходимы дополнительные исследования, так как легирующие элементы могут уменьшить, либо увеличить коэффициент диффузии углерода в мартенсите, который и определяет кинетику распада мартенсита.