Отражение света круговой поляризации от полупроводникового кристалла CdS вблизи экситонного резонанса с учетом пространственной дисперсии

Исследование оптических свойств материалов вблизи фононных, экситонных и плазмонных резонансов является актуальной задачей по причине того, что в этом случае в среде возникают коллективные возбуждения – поляритоны или плазмоны, имеющие смешанный электромагнитный и механический характер. Так, вблизи экситонного резонанса в ряде полупроводников необходим учет пространственной дисперсии [1; 4; 5]. Такой учет приводит к возникновению дополнительных волн, одна из которых является продольной волной. Для корректного описания задачи об отражении определяются дополнительные граничные условия (ДГУ) [1]. Для описания ряда метаматериалов требуется построение математическая модели, которая учитывает гетерогенность, киральность и частотную дисперсию среды [8]. Необходимо отметить, что киральность по сути является эффектом пространственной дисперсии. Возбуждение поверхностных плазмонов и поляритонов вблизи фононных и плазмонных резонансов лежит в основе уникального метода диагностики резонансных сред – метода спектроскопии поверхностного плазмонного резонанса [3; 7], в этом случае возникают узкие резонансные линии в спектре отражения, которые несут информацию об исследуемой среде.

Использование поляризованного излучения при оптической диагностике материалов позволяет получать дополнительную информацию о свойствах материала из-за векторного характера электромагнитного поля. Наибольшее распространение получил эллипсометрический метод анализа оптических свойств материалов [2; 6], позволяющий анализировать сразу два эллипсометрических параметра. Еще большую информацию относительно оптических свойств дает использование света круговой поляризации – в этом случае при отражении возникает свет эллиптической поляризации, ориентация которого несет полезную информацию относительно исследуемой среды [9; 10].

Е^Н © Яцышен В.В., Бородина И.И., 2024

Учет пространственной дисперсии при анализе оптических свойств полупроводниковых материалов приводит к возникновению дополнительных волн, одна из которых является продольной волной [1; 4; 5]. Для корректного описания задачи об отражении требуются дополнительные граничные условия (ДГУ) [1]. В настоящей работе приведены результаты расчета эллипсометрических параметров при отражении света круговой поляризации от среды с пространственной дисперсией.

1.    Постановка задачи

На границу кристалла CdS вблизи экситонного резонанса падает световая волна с левой круговой поляризацией. Требуется найти частотно-угловые спектры эллипсометрических параметров отраженной волны, а также провести анализ изменения формы эллипса поляризации при изменении частоты и угла падения.

2.    Методы решения

Задача решается на основе уравнений Максвелла в среде с пространственной дисперсией.

Диэлектрическая проницаемость кристалла CdS вблизи экситонного резонанса имеет вид [8]:

s ( « , k ) = S o +--

« 0

—

« 2

« 2 — i «_у+« 2 p ²

D ₀

.

Здесь « о - частота экситонного резонанса; го p

–

H = H о exp i ( k — ^— — « t ) .

В качестве плоскости падения мы выбираем плоскость XZ . Поэтому y -составляющая волнового вектора для всех возникающих волн будет равна нулю - k y = 0. Задача разбивается на 2 случая - s - и p - поляризацию. В первом случае имеем следующие значения для компонент поля E: E y * 0, E x = = E z = 0. Для p-поляризации - E y = 0, E x * 0, E z * 0.

Подстановка предполагаемого вида решения (3) в уравнения Максвелла (2) для случая s-поляризации приводит к дисперсионному уравнению:

к ² = к 0 s ( « , к ) .                                               (4)

Здесь к 0 = « / c .

В случае p-поляризации для нахождения дисперсионного уравнения получаем следующее условие:

s ( к 0 s — к ² ) = 0.                                            (5)

Из (5) вытекает существование трех нормальных волн в среде с пространственной дисперсией для p-поляризации: двух поперечных, дисперсионное уравнение для которых совпадает с уравнением (4), и одной продольной с дисперсионным уравнением s ( « , к ) = 0.

Мы рассматриваем случай, когда частота падающего света « близка к частоте экситона «0. В таком случае формулу (1) для диэлектрической проницаемости можно преобразовать к виду плазменная частота; « - частота падающего света; So - диэлектрическая проницаемость кристалла при « ^ »; у - параметр затухания; p - показатель преломления; D0 – параметр пространственной дисперсии:

_ * 2

mc

D o =       ;

ЯГО me - эффективная масса экситона; с - скорость света.

В основе анализа распространения электромагнитных волн в среде лежат уравнения Максвелла:

s ( « , к ) = S 0

Здесь

B

« 2

’0 = 2 , « ² ₀

—*

. —    1 5B rot E = —     , c д t —

^^— г7 1 d D rot H =--

.

c d t

Решение этих уравнений ищем в виде нормальных волн:

E = E o exp i ( кг —« t ) ,

B ₀

^— 2 Y 0 ^— i ^г 0 + р D ₀

0 =

« — « 0

« 0

Г,

Y

⁰   « 0

Показатели преломления для поперечных волн находятся как корни следующего биквадратного уравнения:

р ⁴ — 2 F 1 р ² + F 2 = 0.                                  (6)

Для продольной волны получается следующее уравнение:

^р = F 3 .

В формулах (6), (7) введены следующие обозначения:

^{S    Г} о D o

F 1 = Y 0 D 0 + у + i     ,

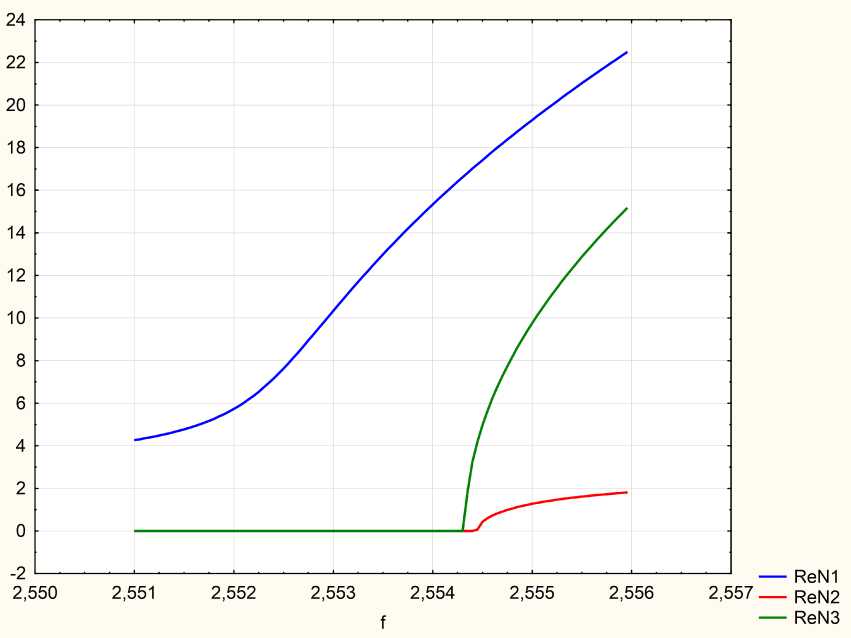
Рис. 1. Зависимость действительных частей величин N i от частоты. Угол падения g = 45 °

Fig. 1. Dependence of the real parts of the N i quantities on the frequency. Angle of incidence g = 45 °

F 2 = 2 Y 0 D 0 ^£ 0 B 0 D 0 + i ^Г 0 D 0 ^£ 0 ,

F 3 =    F 2 *

^£ 0

Дополнительное граничное условие мы выбра- ли в виде следующего условия на поляризацию при z = 0 [1]:

——

P +

1 d P kT ~dz

= 0.

Для s-поляризации используется только y -составляющая уравнения (8), а для p-поляризации – x и z -составляющие. При учете дополнительного граничного условия (8), а также обычного условия непрерывности тангенциальных составляющих векторов E и H задача об отражении решается однозначно.

Результаты расчетов спектров эллипсометрических параметров приведены ниже на графиках 1–10.

На рис. 1–2 показаны частотные зависимости действительных и мнимых частей величин Ni, которые определяются как относительные значения z -компонент волновых векторов — i нормальных световых волн в среде с пространственной дисперсией:

k

N = iz , i = 1,2,3.

i k0

Из этих рисунков видно, что после значения частоты h ^ 0 = 2,5524 eV в среде распространяются сразу три волны, в то время как до этой частоты – только одна первая поперечная волна, две другие, включая продольную, здесь имеют большие мнимые части Im( N_i ) и поэтому не распространяются.

3. Результаты

4.    Обсуждение результатов

Расчет частотно-угловых спектров эллипсометрических параметров проводился для следующих значений параметров, относящихся к полупроводниковому кристаллу CdS:

£ ₀ = 8,3, Й Ю ₀ = 2,5524 eV, B 0 = 1,25 • 10 “2 ,

D ₀ = 1,8 • 10 ⁵ , T = 13,8 - 18,3 i.

Из рис. 3 видно, что угловые зависимости эллипсометрического параметра р при различных частотах значительно отличаются друг от друга, в то время как частотные зависимости испытывают наибольшие изменения в диапазоне частот h a = = 2,554-2,555 eV (см. рис. 6).

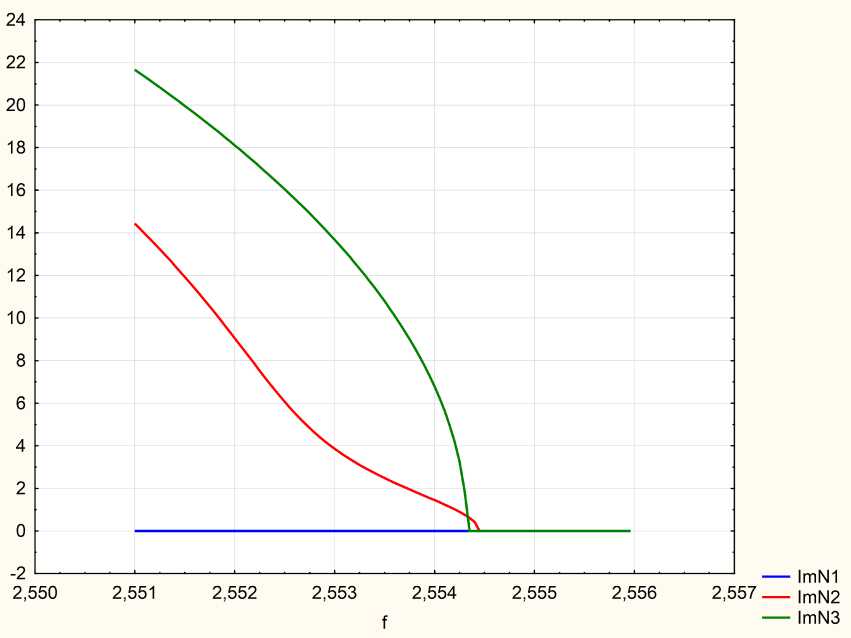
Рис. 2. Зависимость мнимых частей величин N i от частоты. Угол падения g = 45 °

Fig. 2. Dependence of the imaginary parts of the N i quantities on the frequency. Angle of incidence g = 45 °

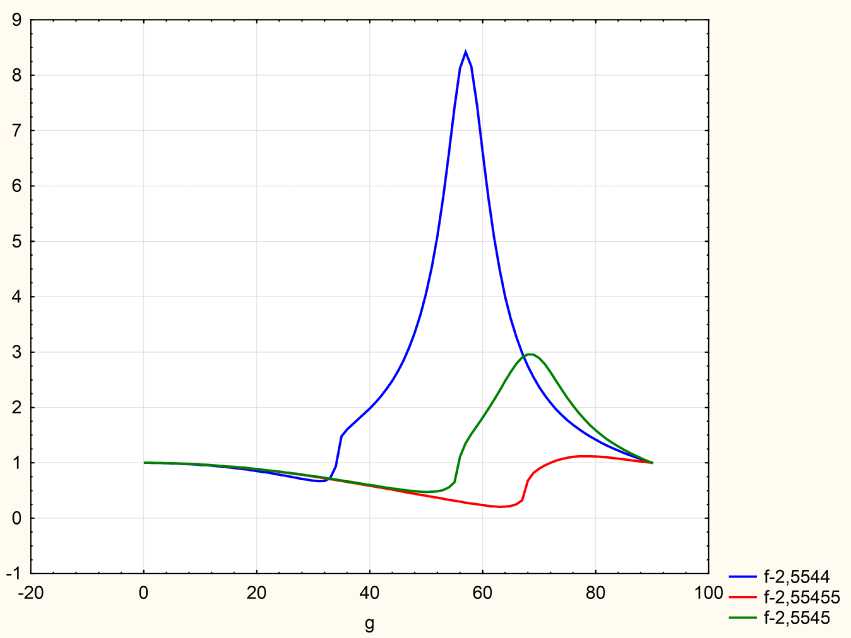
Рис. 3. Зависимость эллипсометрического параметра р от угла падения g для различных значений частоты: Й ® 1 = 2,5544 eV, h ^ 2 = 2,55455 eV, h ^ 3 = 2,5545 eV

Fig. 3. Dependence of the ellipsometric parameter р on the angle of incidence g for different frequency values: h ^ 1 = 2,5544 eV, h ^ 2 = 2,55455 eV, Й Ш 3 = 2,5545 eV

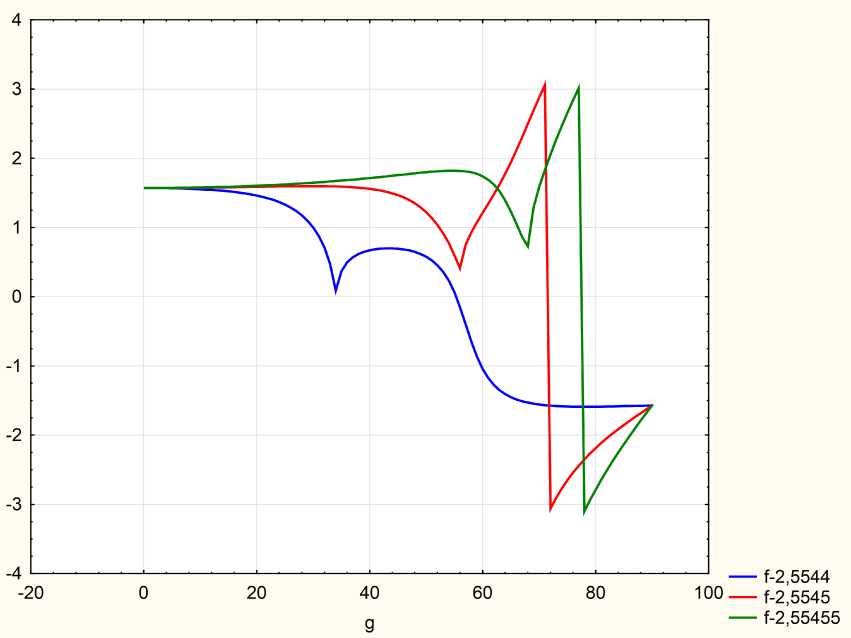
Рис. 4. Зависимость эллипсометрического параметра Л от угла падения g для различных значений частоты: ^ ^ 1 = 2,5544 eV, h ® 2 = 2,5545 eV, h a 3 = 2,55455 eV

Fig. 4. Dependence of the ellipsometric parameter Л on the angle of incidence g for different frequency values: Й Ш 1 = 2,5544 eV, h ^ 2 = 2,5545 eV, h a 3 = 2,55455 eV

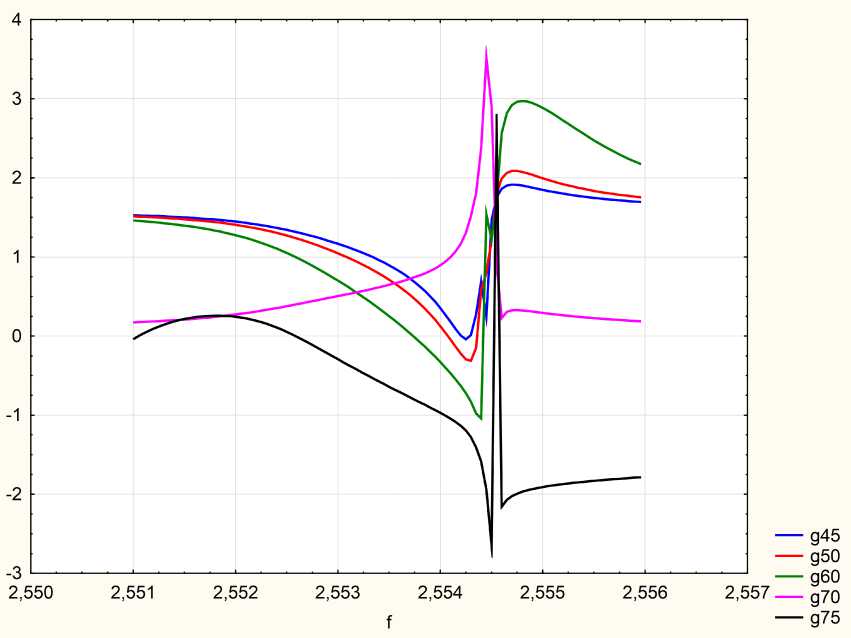
Рис. 5. Зависимость эллипсометрического параметра Л от частоты при различных углах падения g = 45 ° , 50°, 60°, 70°, 75° Fig. 5. Dependence of the ellipsometric parameter Л on the frequency at different angles of incidence g = 45 ° , 50°, 60°, 70°, 75°

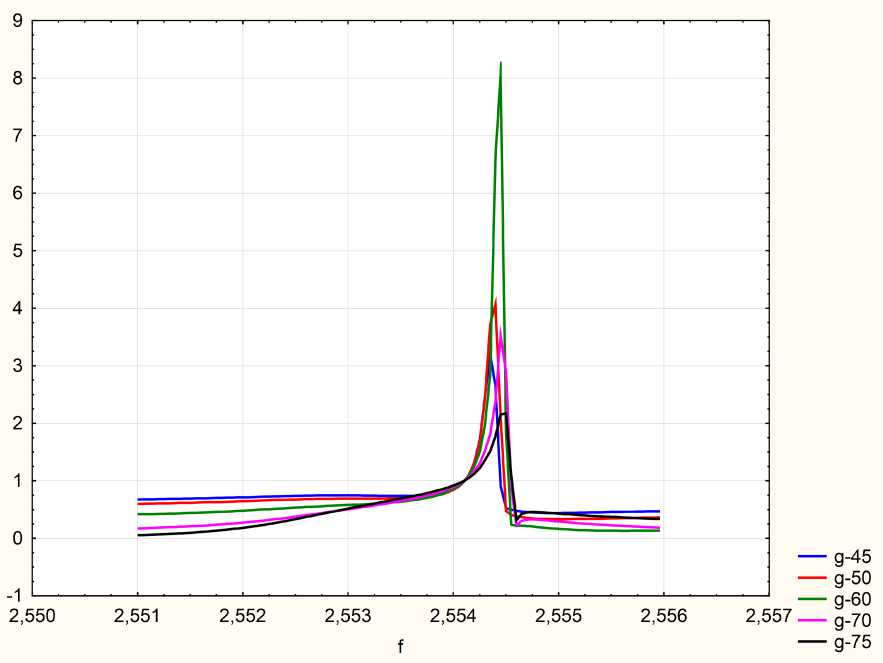
Рис. 6. Зависимость эллипсометрического параметра р от частоты при различных углах падения g = 45 ° , 50°, 60°, 70°, 75° Fig. 6. Dependence of the ellipsometric parameter р on the frequency at different angles of incidence g = 45 ° , 50°, 60°, 70°, 75°

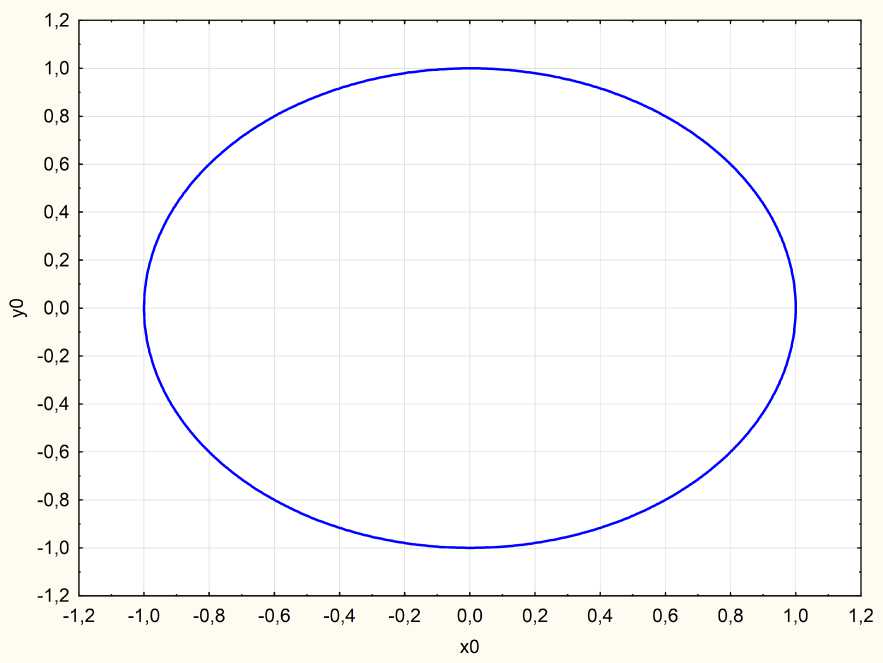
Рис.7. Круговая левая поляризация падающей волны

Fig. 7. Circular left polarization of the incident wave

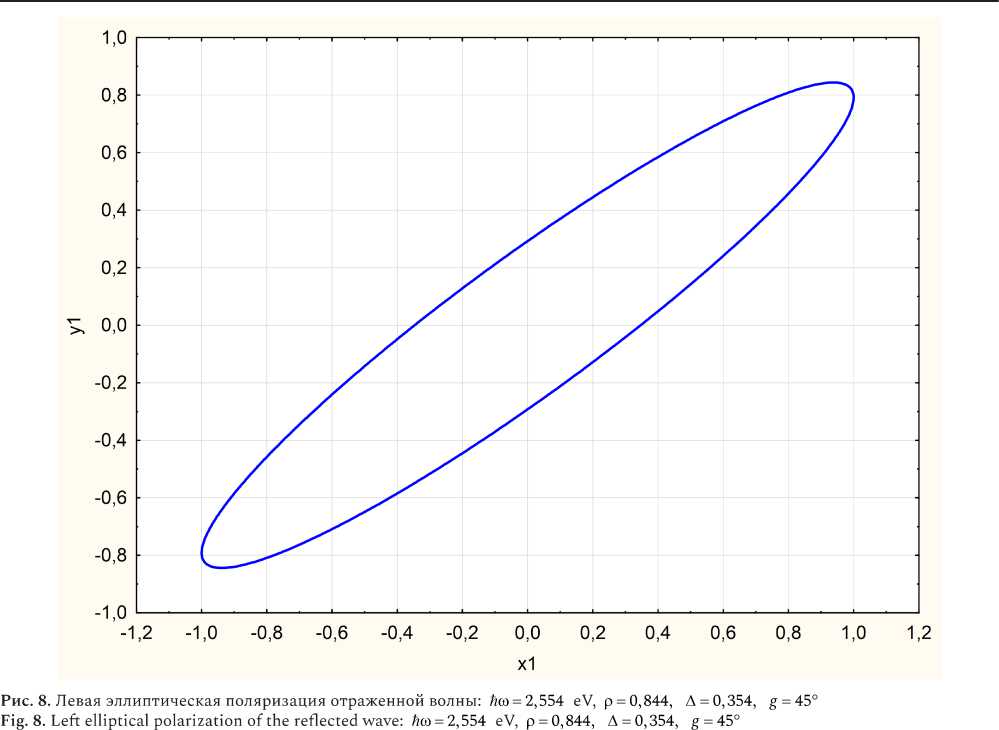
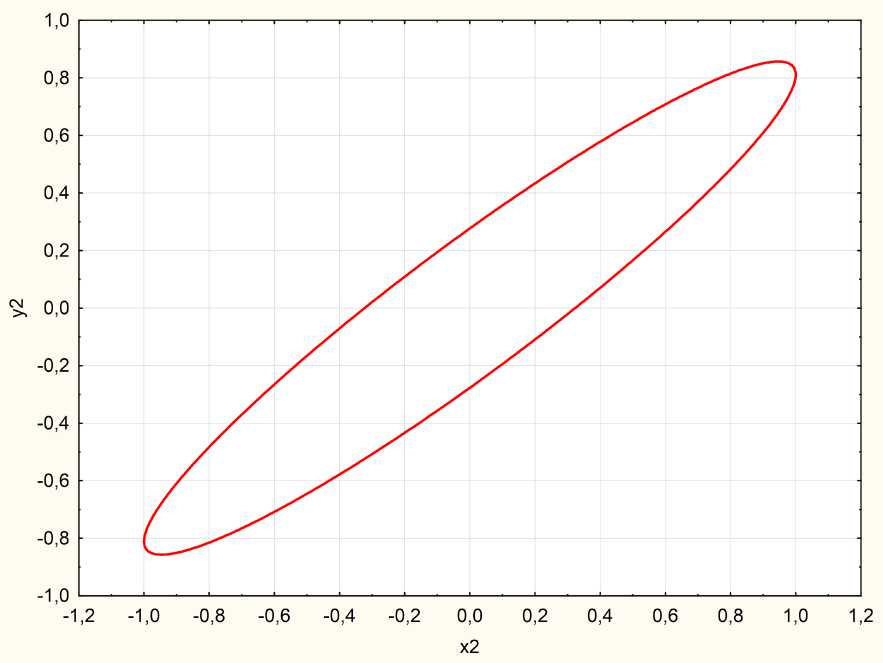
Рис. 9. Правая эллиптическая поляризация отраженной волны: Й ш = 2,554 eV, р = 0,857, Л = - 0,329, g = 60 °

Fig. 9. Right elliptical polarization of the reflected wave: Й ш = 2,554 eV, p = 0,857, Л = - 0,329, g = 60 °

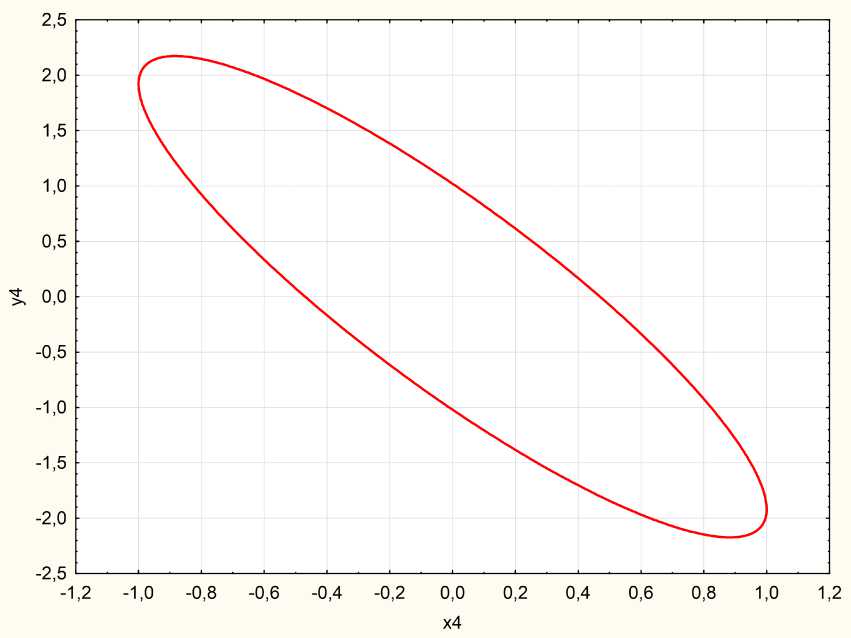
Рис. 10. Правая эллиптическая поляризация отраженной волны: h & = 2,5545 eV, р = 2,173, Д = - 2,653, g = 75 °

Fig. 10. Right elliptical polarization of the reflected wave: h ^ = 2,5545 eV, p = 2,173, Д = - 2,653, g = 75 °

Следует обратить особое внимание на сильную изменчивость второго эллипсометрического параметра Д (рис. 3) как от угла падения, так и от частоты (рис. 5). Это приводит к тому, что отраженный эллипс поляризации может значительно менять свою конфигурацию в зависимости от частоты и угла падения. Это продемонстрировано на рис. 7–10. Первоначально на среду падала световая волна круговой поляризации.

Из приведенных рисунков видно, что характер эллипса поляризации существенно зависит от частоты падающего излучения и от угла падения.

Заключение

В работе приводятся результаты расчетов частотных и угловых спектров эллипсометрических параметров отраженного света для полупроводникового кристалла CdS вблизи экситонного резонанса с учетом пространственной дисперсии. Показано, что эллипсометрические параметры обладают высокой чувствительностью к характеристикам среды с пространственной дисперсией и могут служить для интерпретации экспериментальных данных.