Parallel algorithms of integer arithmetic in radix notations for heterogeneous computation systems with massive parallelism

Reliable computations are the necessary [1] and sufficient [2-4] tool for algorithmic analysis of large scale unstable problems. The library "Exact computation" [5] provides such functionality in the distributed computing environment.

Further increasing of effectiveness of such software is possible for account of heterogeneous computing environment allowing to parallelize local arithmetic operations using more than one process for the basic arithmetic operation.

Quality measure of the secpiential algorithm is its computational complexity. Less computational complexity leads to less time complexity of the algorithm and its more efficiency. Computational complexity of parallel algorithm is not indicative since different operation may be performed simultaneously. Good quality measure of the parallel algorithm is given by measure of the strong scalability of the parallel algorithm is speedup over sequential analogs. The best parallel algorithms provide constant or logarithmic (from the input data size) estimations of the time complexity that leads to O ( n ) оr O ( n/ log₂ n ) speedup. Linear O ( n ) speedup usually is given by fully parallel algorithms and O ( n/ log₂ n ) speedup is given by algorithms that use doubling scheme.

If the processes k = 0 , 1 ,... ,n require time tk for the performing of operation p then time required to complete operation is t^p = max {t^p_k : k = 0 , 1 ,..., n}.

The subject of the paper is development of the completely scalable parallel algorithms of the basic arithmetic operation with linear O ( n ) speedup and the well scalable parallel algorithms with O ( n/ log₂ n ) speedup.

It is demonstrated that the application of redundant positional notations gives the completely scalable addition/substr action algorithms and relative scalable algorithms for the rest basic arithmetical operations. The results about scalability algorithms for integer arithmetics that were announced at the conferences [6-8] are presented in the paper.

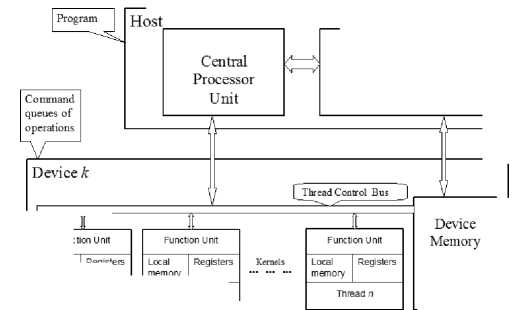
1.    Heterogenous Computation Systems

Structure of heterogenous computation systems is presented on fig. 1. Heterogeneous

Host Memory

Program

Central Processor

Command queues of operations

Device к

Thread Control Bus

Device Memory

Function Unit

Local memory

Registers

Kernels

Local memory

Local memory

Thread

Fragment of heterogenous system architect computation system unit consist of the managing CPUs (host side) and the set of devices (device side). CPU provides operating system functioning and program launch. Devices provide parallel execution of basic operations over the data objects of program.

Data exchange between host and device memory is carried out via PCI bus, On-chip and device-device communication is carried out via DMA (direct memory access). All local on-chip interprocess communications of the "point-to-point" type can be carried out asynchronously. Collective "one-to-all" data exchange may be carried out in two steps. First, some process sends data to the shared thread or shared device memory. Second, recipients read transmitted data. Reading of message from the shared memory may be performed simultaneously by all recipients.

In summary, such geterogeneous system allows to construct a relatively low-cost, high-performance computer with low power consumption. However, the transfer speed between the host CPU and the massive parallel device can become a bottle neck, making it unusable for applications with intensive CPU-Device-CPU data flow.

Massive parallel architecture of the devices requires algorithms with high level parallelism. Less clock rate (than CPU clock) of the device processors also decrease its efficiency for sequential tasks.

Features of the devices may dramatically vary from one to another therefore we consider only pseudocode of algorithms.

2.    Analysis of Parallel Algorithms for Integer Arithmetic Operations in the Classical Radix Notation 2.1.    Addition of the Nonnegative Number

Classical addition algorithm for n -digit numbers is fully sequential. The possible approach for parallel execution of the addition is two step procedure: first one is parallel digit-by-digit summation, second one is parallel carry propagation from all digits where carries are non zero. The second step can be performed after the first one is completed but the operations at each step are fully parallel.

Algorithm may be implemented by the two fully parallel procedures Digit_Addition and Carry_Propagation. Some global procedure _global_Add is need to define lengths of the summands and create the required quantity of the parallel processes. Further it is required to call procedure _global_Add to get the result of addition ( a_{n -} 1 ... a ₀) R + ( b_{m -} 1 ... b ₀) R. Lets estimate the time for the execution of such algorithm as well as possible speedup compared with classical sequential algorithm.

It is known that the binary notation is applied for presentation of numbers in computer memory. Therefore the value R = 2 ^r is accepted as the base of the radix. Here r is word length of the utilized registers. Usually modern computers use 32- or 64-bit registers. We use the noted values of R and r.

Thus, each of parallel processes of the procedure Digit_Addition requires time for the addition of single digits and calculating corresponding digit of the result and carry, denote it as ts. The time of the execution of procediire Carry_Propagation can vary from 0 in the best case to (n — 1) • ts in worst case, we neglect overhead for while loop. An Full time of execution of addition algorithm depends on values of input arguments. The full time varies from s to n • s plus overhead on fork of the process. Time of the execution of addition by strictly sequential algorithm (i.e. digit after the digit) in above terms is exactly n • ts. Lets estimate the mean time of the execution of our parallel algorithm on the for

assumption that the arguments belong to uniform distribution. Assume that n = simplicity.

m

The probability of the non zero carry in one of the processes is equal to

2 ^r - 1

p = P {a + bi > 2r} = ^ P {ai l=1

2 ^r - 1 ₁

= l} P {bi >  2 ^r — l} = E2 r •

i =1

l

2 r

.

Probability to have sum of two digits ai + bi = 2 ^r

^^^^^^

1 is equal to

2 ^r - 1

q = P {ai + bi = 2^r — 1 } = ^ P {ai = 1} P {bi = 2 ^r l =0

^^^^^^^^^r

2 r

1—i} = E l=0

2 r

•

2 r

2 r

.

Consider the probability of carry propagation chain with length k > l

Pl = P

{ n-l- 1 г                          i

U  (ai + bi > 2 r - 1O i=o L                     j=1

j =1

ai + j + bi + j = ² r ^— 1)]   = ⁽ n

^{— 1} ) pq^l.

Modern processors can address up

to few terabyte of operating memory but we probabilities Pl < ql 1, l = 0, 1,... ,m even for very long numbers when the digit r-bit number where r = 32 оr r = 64.

have is an

It is easy to see that the value of the probability P 2 < q , therefore, in the asymptotic behavior the mean execution time of the algorithm is equal to 2 ts. Thus, the considered algorithm has at the average n/ 2 speedup in comparison with the sequential addition algorithm.

Time of the addition in the the worst case may de decreased due to the improvement of the carry propagation algorithm. Elements of the chain of sequential carries may be processed in parallel. Carry propagation chains don’t overlap.

Algorithm AGP releases advanced carry propagation scheme.

T CPI. Set L = 1. assiline V ( i ) = i for each process i = 0 , 1 , 2 ,... ,n.

T CP2. While exist i = 0 , 1 , 2 ,... ,n with ci = 1. for all i : i = ( L — 1) mod 2 L perform steps ACP3-ACP5.

T CP3. Set j = min {i + L, n — 1 }.

ACPJ.l. If Ci = 1 then set sv ( j ) = tv ( j ) + 1 = ^ V ₍ j ) sV—j) ... s V ₍ j ) s V ₍ j ^2 , cv ( j ) = ^sV ( j ) ,tv ( j ) = ( sr— 1) ... s V ( j ) ^s V ( j )) , ⁽ ^k ^: i<^k (^j)) (tk =^{0 ,c}k =^{0) ,V} (^j) = V (i).

ACPC2. Else if Ci = 2 ^r — 1 о г V ( i ) = i. set V ( j ) = V ( i ).

ACP5. Set L=2L.

ACP6. Stop.

Under joining the low process with index L 2 ^k sends to higher process with index ( L + 1)2 ^k absent ripple can’y flag mark it as NotCarry. itself carry c. and possible ripple carry verge V. High joining process with index ( L + 1)2 ^k in the case of the presence of transfer from the low-order fragment L 2 ^k is produced into all necessary digits (from L 2 ^k + 1-th to V (( L + 1)2 ^k )-th). The verge of the propagation of the ripple-through carry in the united fragment is also refined. Excess processes are terminated for all cases.

Lets examine time complexity of addition with advanced carry propagation procedure. This loop is carried out by any of the processes not more than ( log₂ nj times. During the appropriate optimization at heterogeneous environment these operators can be executed in parallel for one tick. Each of the active processes also executes no more than one receiving communication and not more than one sending communication. Their preparation and execution can be carried out for two tics.

Thus, the mean time of the advanced carry propagation scheme is equal to 3 s , and in the worst case it is equal to 3 s( log₂ nj.

In the asymptotic behavior of the mean time of the execution of addition with the application of advanced carry propagation algorithm is equal to 4 s , i.e., exceeds mean time with the application of simple carry propagation algorithm in 4/3 times. However, already with the presence of the carry circuits of length of more than two digits the effectiveness of advanced carry propagation algorithm usage is undoubted.

• 2.2.    The Binary Relations

• 2.3.    Determination of the Number Significant Digits

Checking truth of any binary relation apb : p G {<, <, = , >,>, = } may be carried out through the relations p G { = , >} . Indeed ( a <  b ) = — ( a > b ), ( a = b ) = — ( a = b ), ( a > b ) = ( a > b ) V ( a = b ). ( a ) = — (a > b).

Idea of the algorithm is following. Initially data are split up n separated processes i = 0 , 1 ,... ,n — 1. aiid pi arid qi are results of comparisons pi = ( ai = bi ) aiid qi = ( ai > bi ) for fragments i = 0 , 1 ,... ,n — 1.

The k -th iteration of the algorithm handles the fragments associated with the processes of 1 2 k arid ( l + 1)2 k and combines them to one fragnlent associated with the process 1 2 k- 1. Values of pi anid qi are recalculated by formulas r = p2i ₊₁& p2i. s = q2i ₊₁ 1 ( p2i ₊₁& q2i ). P 2 i +1 = true- p 2 i = true- q 2 i +1 = false- q 2 i = false, pi = r. qi = s.

Sequential comparison algorithm requires at mean n/ 2 operations of digit comparison. It is easy to see that palallel algorithm requires [ log₂ n) of parallel steps. Average speedup over the sequential algorithm is n/ 2 \ log₂ n) times.

For the efficient usage of computational resources under execution of arithmetic operations it is necessary to know the number of significant digits.

Number of significant digits of the difference after subtraction can be determined only after operation completion. Therefore, the way to compute completion is an important part of the efficient arithmetics.

Algorithm for this operation is optimized simplified version of the binary relation algorithm which requires P log₂ n) of parallel steps. So determination of the number of significant digits is used only straight after the subtraction operation and may be performed with P log₂ n) parallel steps.

• 2.4.    Multiplication of the Multidigit Number on the Digit

Algorithm M calculates the product ( c_n,...,c 0) R of given non-negative integers a = ( a_n- 1, ...,a 0) R. aiid b = ( b 0) R represented in the radix notation with the base R = 2 ^r.

Ml [Initialization], Fork n I 1 proceses.

М2 [Digit-on-digit multiplication]. Each process i = 0 , 1 ,...,n — 1 calculates ( ^x1 x ⁰⁾ r = ^a [ i 1 [ i 1 • b.

М3 [Addtition]. Each process i = 0, 1,2,..., n — 1 calculates f [ i 1 = c[i1 =

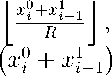
mod R.

Mi [Carry propagation]. Each process i = 0 , 1 ,..., - — 1 sets c [ i + 1] + = f [ i ] .

M5 [Finish], ( c [ n ] c [ n — 1] ... c [0]) _R is result of the algorithm.

Algorithm calculates product of the number b on the digits ai, i = 0 ,... ,n — 1 (line 3). Product of two digits is a two-digit number ( x 1 x 2) _R<  (2^r — 1)2 = 2 ^r (2^r — 2) + 1, i.e. value of the carry x 1 (lines 4,9, and 10) is not more than 2 ^r — 2. Therefore there are no carry propagation chains (lines 11, 12, 13. 14) with length more than 1 and we have ti <  2 ^r — 1 for all i = 0 ,... ,n — 1 ,n.

From the description of Algorithm M it is evident that the expenditures of time for stages M2-M4 is tm + 2 ts where tm is time to calculate the result of the digit on digit multiplication and ts is time to calculate sum of two digits and carry. Thus Algorithm M has speedup n times over sequential algorithm of calculating number on digit product.

• 2.5.    Multiplication of the Two Multidigit Numbers

• 2.6.    Division

We can calculate the product of the two multidigit numbers of length n and m correspondingly using Algorithm M and reduction scheme to calculate sum of the partial results.

The time of execution of such procedure consist of time to perform in parallel Algorithm M for all digit of one number and [ log₂ m] additions of ( n + m — 2)-digit numbers.

Thus, average execution time does not exceed tm + ts (2 + log₂ m ). In the worst case execution time not exceed the value tm + ts (2 + ( n + m )log₂ m ).

Algorithm M uses n and there are m digit to multiply first number on. Consequently, the total quantity of created processes is equal to mn.

In the worst case with increasing length of operands the time of execution slightly exceeds the linear function, whereas execution time of the classical sequential algorithm of multiplication of two numbers has the quadratic dependence on length of operands.

The classical algorithm of the long division cannot be performed in parallel. It requires ( n + m — 1) sequential operations of the inultiplicatron-subtraction with m -digital numbers. In the papers [7, 9] the solution of the problem of increasing of the effectiveness of the algorithm for the operation of division by means of the Newton’s method application is proposed.

In order to divide integer u =   (u[n — 1] u[n] ... u[1] u[0])R by integer v = (v[m — 1] ... v[0])R it is proposed to find sufficiently precise approximation for number 1 /v. then to multiply it on u. which vail give the approximation for u/v. It is obvious that the length of integral answer is not more than n — m + 1. Number 1 /v contains not more than m nonsignificant zeros in the high-order digits, for obtaining the correct result of division it is sufficient that the approximate value of 1 /v would still contain at least n — m + 1 significant digits. Thus, the necessary precision of the value 1 /v is determined by value R-n+1.

The application of Newton’s method to the problem of finding of the root of equation f ( x ) = 0, where f ( x ) = v — 1 /x, consists of the sequential calculation of

Xk+i = (2 — v • Xk) • Xk, k = 0, 1, 2,..., where x0 is initial approximation calculated with the necessary precision. Function f (x) = v — 1 /x is twice continuously differentiable arid strictly convex when x > 1. In this case the Newton’s method possesses the quadratic speed of convergence, i.e., a quantity of correctly calculated discharges after the execution of sequential iteration will double. The initial approximation x0 = 1 /(v[m — 1]) of value 1 /v has an error

1               1

v [ m — 1] • Rm ^{- 1}    v

v - ^{v [ m} - ^1] • Rm ¹ _<       1      _{<  R} -m +1

v • v [ m — 1] • Rm ^{- 1} ~ v • v [ m — 1] ^—         ’

• i .e. it correctly calculates m digits. Thus, a quantity of iterations, which it will be necessary to carry out according to the Newton’s method, will be not more than the value 4log2( n + 1) ~ log2 m.

On the k-th itei айгои (k = 0, 1, 2,.. .,l < log2( n + 1) — log2 m) variable x represents (2k+1 — 1)-digit number. Therefore at this cycle body with aid of parallel algorithms one operation of multiplication of variable x by the m-digit number b, one operation of subtraction of (2k)-digital numbers, arid one ojaeration of multiplication of (2k)-digital numbers are performed. Consequently, time necessary for fulfilment of the cycle body does not exceed value 2tm + ts • (2 + log2 m + k) at the average ease 2kk + 2, 5 • 2k + 3m log2 m + k) at the worst case.

and value 2 tm + ts • (4 +

Since

l k·2k ≤ k=0

lb k = ^, k=0____________ ll k2    4k k=0   k=0

l b 2k = 2l+1

k =0

- 1 ,

/ 2 1 3+3 1 2 +1   4 l +1 - 1

V 6      •   3

< 2 ^{l +1}      ,

the time of execution in the average and the worst cases will not exceed the values O (log₂ n • log₂ ( n +)) ar id O ( n + log₂³ / ² ( n+ )) respectively.

The multiplication of two n -digit numbers completes the execution of procedure D. This step requires at the average O (log₂ n ) time and O ( n • log₂ n ) in the worst case. Thus, the final estimations of the execution time of division in the average and worst cases will lie equal respectively O (log₂ n • log₂ ( n + )) ar id O ( n+ log₂³ / ² ( n +) + n log₂ n ).

3.    Usage of Sign Radix Notation

The notation system given above is unsigned, digits in the position system on the base R are numbers 0 , 1 , 2 , ..., R — 2 , R — 1. One of the drawback of this is that it requires the comparison of numbers to find the result of addition and subtraction. It may be avoided by the application of sign radix notation. The digits on the sign radix notation on the base R are integers

-

R

-

R

+1 , ...,- 1 , 0 , 1 , 2 ,...,

R

- 2 ,

R

- 1 .

Note that with odd R the number of positive and negative numbers is equal, and with even R a number of positive numbers is less than the number of negative ones.

Designate presentation of the number at the sign position radix notation with base R = 2 r as ( a_n- 1 ,..., a ₀) ±_R. arid its digits as ai = ( аГ ^{- 1} ar ^{- 2} ... a ¹ a ⁰) ± ₂. i = 0 , 1 ,... ,n — 1. High bit of the digit presentation is its sign (0 for positive, and 1 for negative). So digits at the sign radix notation are the objects of the sign integer type.

Note that all basic algorithms, for the unsigned numeration systems, with exception of the algorithms of addition / subtraction, will not change. The algorithms of addition / subtraction are united into the common algorithm.

Addition procedure calculates the sum of the unsigned presentations of signed integer data type (i.e. for positive numbers in high-order digit zero, for negative numbers in the elder ones digit), and forms the sum and carry into the next digit: in the absence register overflow the carry is zero, the sign of result does not change, but in its presence the sign of result changes to the opposite and the carry of the corresponding sign is formed.

Application of sign position systems simplifies the algorithm of algebraic addition, but it does not solve the problem of ripple-through carries propagation.

The accelerated calculation of the chain of ripple-through carry and its propagation is possible also for unsigned systems. Advantages and disadvantages of the accelerated carry propagation are the same as for unsigned radix notation. The truth of binary relations in the sign systems is easily realized by means of the subtraction operation. The sign of the number is determined by the sign of high-order digit. Algorithms of definition of a number of significant digits, multiplication and division are the same as in the unsigned radix notation.

4.    Usage of Redundant Radix Notation

Parallel algorithms of all arithmetic operations presented above show at the average high speedup over sequential versions. Mean computing time of results of addition, subtraction, multiplication by the single-column number has the value O (1), the mean computing time of binary relations has a value of O (log n ), multiplication and division of the numbers of word length n does not exceed value O (log2 n ). However, in the worst case the computing time of results of any operation with n -digital numbers requires O ( n ) time with the usual carry propagation and O (log₂ n ) with the accelerated carry propagation. The reason for deviations from the average value is the fact that with the execution of addition (subtraction) for carry propagation there appear the chains of the length of more than one. To exclude the noted precedents to the usage of redundant radix notation [7] is helpful.

The natural n-digital number N in the radix notation with the base R is presented in the form of ordered set of numbers n-1

N = ( an- 1 ... a i a 0) r ⁼       aiR, an- 1 , ..., a 1 , a 0 G D = { 0 , 1 , 2 ,..., R — 1 } .

l =0

This presentation is unique. The uniqueness of presentation is reached because the set of numbers D contains exactly R elements that present the section of natural series including zero. The expansion of the set of numbers D will lead to the expansion of presentation for number N.

Consider the method of expanding of the set of numbers D, which makes it possible to perform the operation of addition (subtraction) in time O (1). Let the computing system use 2 ^r -bit registers. Let us ac-cept the number base R = 2 r- 1. Therefore any digit ai has non-redundant representation (0 ar- ² ... a ¹ a0)2. Under redundant representation we suppose that ai may Ire presented with possible nonzero delayed carry ar- 1. so ai = ( ar ^{- 1} ar- ² ... a ¹ a ⁰)2.

Look over one of the possible methods of realization of addition algorithm. Let the г-th digits of terms have form ai = (ar1 ar-2 ... a] a0)2, bi = (br-1 br-2 ... b1 b0)2

• i .e. present binary r -digital numbers. After completing of digit-by-digit sum in each position there will be obtained an ( r + 1)-digital result

si = ai + bi = ( ar- ¹ ar- ² ... a a ⁰)₂ + ( br- ¹ br- ² ... b ¹ b' ) 2 = ( sr si- ¹ ... s ¹ s ⁰)₂ .

Use two elder bits for the transfer into the next digit, and obtain resulting r-digital form r-2 r-3       1 0         r r-1         r-1 r-2       1 0

si            si    si ...  si si 2 ⁺   si- 1 si- 1  2 si    si     ... si si  2 .

Thus, executing the operation of addition may be performed fully parallel for all cases.

Presented approach uses a radix notation with the redundant digit set. We use of the redundant bit of the digit as the postponed carry that makes it possible to perform the operation of addition in constant time.

Since the algorithms of multiplication and division are correct in this numerical notation and contain the operation of addition only, i.e. use makes the time of the execution of these operations is not worse than those estimations of the mean time of execution for algorithms examined above.

Disadvantage of the redundant radix notation is in the plurality of the number presentation, which makes effective calculation of binary relations and quantity of significant places possible only after the global carry propagation, that removes the redundancy of representation. Let us recall that in the asymptotic behavior the probability of appearance of additional carry approaches zero.

Conclusion

Effective realization of local arithmetic operations with big numbers requires device with enough amount of random-access memory. If the numbers are so huge that the volume of device’s random-access memory is not sufficient then operations may be performed on several devices. Moreover, interface between the central processor and the device or between the devices has restrictions on capacity, latency and bandwith. The effectiveness of arithmetic operations with huge numbers is a subject of further researches. It is possible that implementation of Toom-Cook or Karatsuba rapid multiplication algorithms [9] will be effective for this case.