Параллельные вычисления в задаче анализа движения механической системы в случайной термовязкоупругой среде

Хорошо известно, что современные задачи науки и техники, включая проблемы механики деформируемого твердого тела, требуют для своего решения удобного и эффективного теоретического и прикладного аппарата. Такой прикладной аппарат включает принципы применения компьютерной техники различной производительности для реализации вычислительных алгоритмов. Особое внимание направлено на развитие и применение высокопроизводительной вычислительной техники, а также алгоритизацию и

(с) Полосков И. Е., Полосков И.И., Soize С., 2015

программирование для использования параллельных, распределенных, облачных и других вычислений. Необходимость решения все усложняющихся задач, включающих исследование детерминированных и стохастических объектов с вязкоупругими свойствами, приводит к внедрению указанной вычислительной техники и программирования в повседневную практику.

В настоящее время существует немало примеров, когда анализ объекта в чисто детерминированной постановке не является достаточным. Во всякой реальной динамической системе существуют случайные флуктуации различного характера, в том или ином смысле малые по сравнению с неслучайными факторами, но оказывающие определенное отрицательное воздействие на работу системы. Математический аппарат для исследования таких объектов дает теория случайных процессов и полей и, в частности, теория стохастических дифференциальных уравнений (СДУ).

Очевидно, что необходимо искать эффективные способы решения систем стохастических дифференциальных уравнений и стохастических интегро-дифференциальных уравнений (СИДУ), обыкновенных и в частных производных. Выяснилось, что значительный прирост скорости расчетов достигается за счет использования параллелизма в алгоритмах прямого численного решения СДУ. При построении решений СДУ используют многократное моделирование процессов из реальных задач, что и дает гибкие возможности для распараллеливания решения СДУ на современных вычислительных устройствах.

Цель написания данной статьи - представить технику применения параллельных вы числений для приближенного вероятностного анализа поведения одной динамической механической системы с учетом термовязкоупругости среды. Для изучения указанной системы, описываемой линейными СИДУ, использовались разработанные модификации итерационного метода аппроксимации функций Грина [1] и полунеявого метода Эйлера-Маруямы в сочетании с методом статистического моделирования (Монте-Карло) [2, 3] и статистической обработкой результатов расчетов [3]. В работе представлены общее описание модели, схема использования известного пакета компьютерной алгебры Mathematica [4] для подготовки вычислений в рамках стандартных систем программирования (на базе языка Intel Fortran), кратко описаны алгоритмы и методология использования параллельных вычислений, приведены некоторые результаты экспериментов с этими средствами на компьютере с центральным процессором, имеющим четыре ядра, и полученные выводы и рекомендации.

O

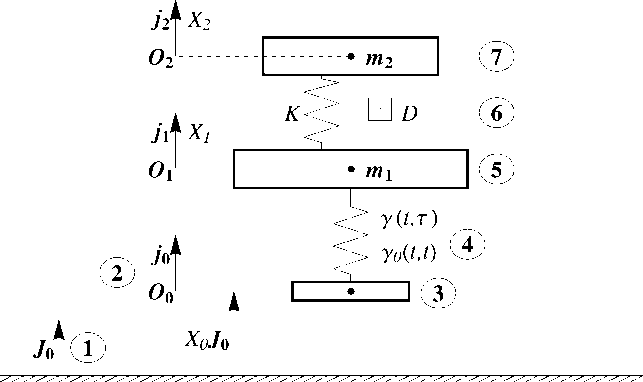
Рис. 1

1.    Описание модели

Рассмотрим механическую систему, изображенную на рис. 1, где 1 - абсолютная система координат, 2 - относительная система координат, связанная с подвижным основанием, 3 - подвижное основание, 4 - термовязкоупругая компонента, 5 - первое тело,6 - упругая диссипативная механическая ком понента, 7 - второе тело. Система, модель которой разработана третьим из соавторов этой статьи, состоит из двух твердых тел массами m 1 > 0 и m2 > 0 соответственно. Каждое тело имеет только одну степень свободы, соответствующую его перемещению в одном заданном направлении. Первое тело связано со вторым телом и подвижным ос- нованием. Связь между телами состоит из линейной упругой диссипативной механической составляющей, которая моделируется линейной пружиной с постоянной жесткостью K > Си линейным демпфером вязкого типа с постоянным коэффициентом демпфирования D > С. Связь между первым телом и подвижным основанием состоит из термовязкоупругой механической составляющей, которая характеризуется функциями времени yо (t, т) и y(t, т). Структура этих функций будет представлена ниже вместе с определяющими уравнениями.

Вводится абсолютная система отсчета, для которой единичный вектор основания, соответствующий рассматриваемому смещению, обозначается через J. Подвижное основание движется в направлении J. Также выбирается относительная система отсчета, связанная с подвижным основанием. Его единичный направляющий вектор обозначается через j

Линейная динамика этой механической системы анализируется относительно опорной конфигурации, которая соответствует статическому положению равновесия, причем предварительные напряжения механических компонентов отсутствуют.

Начальное время для временной эволюции выбирается в точке t о = С. В абсолютной системе отсчета в момент времени t смещение подвижного основания обозначается через X о( t ) J. В относительной системе отсчета, связанной с подвижным основанием, в момент времени t смещение первого (второго) тела обозначается через X i( t ) j (X 2( t ) jY

Для построения определяющего уравнения термовязкоупругой механической составляющей предположим, что нижний конец этого компонента предполагается фиксированным, а верхний является свободным и подвергается в момент времени t воздействию силы F ( t ) j о, вызывающей смещение X 1 ( t ) j 1- Используя неизотермическую теорию линейной вязкоупругости [5-8], определяющее уравнение можно записать в виде

F ( t ) = Y о ( t,t ; Q ) X 1 ( t ) +

+ / y ^{( t,T} ; ^Q ) X i^{( т} ) d ^T , t e ^{(c ,T} ] , t 0

где y ( t, т ; Q ) - положительно определенная функция, которая задана при С < т С t С T и предполагается бесконечно дифференцируемой по t и т:

y ( t.^ Q )= ^д '_:;^Q

- отрицательно определенная функция, которая 'задана при С < т С t С Т п поэтому интегрируема по т иа. (С , t ] для лтобого t из (С ,Т ] Q - случайный векторный параметр, представляющий неопределенности в структуре функции y о aiк! y-

2.    Уравнения движения

Пусть Uj ( t ) = dUj ( t ) /dt -скорость, a Uj ( t ) = d ² Uj ( t ) /dt ² - ускорепне тела j jj = 1. 2).

Вследствие того, что движение изучается относительно системы отсчета, соответствующей статическому положению равновесия, при отсутствии предварительных напряжений механических компонент считается, что в начальный момент времени смещения и скорости равны нулю. При этом уравнения движения относительно указанной системы отсчета будут иметь вид ( t 6 (С ,Т ]):

m 1 [ U1 ⁽ t ) + Us ⁽ t )] = ^{— K} [ U 1⁽ t ) ^— U 2⁽ t )] ^—

^{— D} [ U 1⁽ t ) ^— UY 2( t )] ^—y о⁽ t, t ; ^Q ) U 1⁽ t ) ^—

^- У y ⁽ Yt ; ^Q ) U 1^{( т} ) ^dт,

(2.1)

m 2 [ ^U 2 ⁽ t ) + ^U s ⁽ t )] = ^{— K} [ ^U 2⁽ t ) ^{— U} 1⁽ t )] ^—

-DU ( t ) - U1 ( t )] ,        (2.2)

а начальные условия -

U 1(С) = U 1 (С) = U 2(С) = U 2(С)=С .   (2.3)

Пусть ш 1. ш2- ^ ii ^ - положительные дей ствительные параметры, такие что ш 1 = У K/m 1, ш 2 = У K/m 2,

С = D/ (2 m 2 ш 2) , ц = m 2 /m 1 , а до( t,T ; Q ), д ( t,T ; Q ) - функции, получаемые так:

7о^{( t,T} ; ^Q ) = y о^{( t,T} ; ^Q ) ^m 1 ,

7^{( t,T} ; ^Q ) = y ^{( t,T} ; ^Q ) ^/m 1 .

Используя эти обозначения, уравнения (2.1) и (2.2) могут быть переписаны следующим образом:

U 1( t ) = - 2 Ы¹ / 2 ш 1 [ U 1( t ) - U 2( t )] -

- /о^{Y (} t ^Т ; Q ) ^U i^{( т} ) d ^T - ^{U s (} t ) , ^U 2 ⁽ t ) = - ² ^W 2 [ ^U 2⁽ t ) - ^U 1⁽ t )]

(2.4)

-

-^2 [ U2 ⁽ t ) - U 1( t )] -Us ( t ) .     (2-5)

Ускорение Us (t) подвижного основания моделируется нестационарным центрированным гауссовым случайным процессом второго порядка. {Us(t),t G (0,T]} так:

^U s ⁽ t ) = g ⁽ t ) V ⁽ t ) , где g ( t ) - действительная функция, определенная на. [0 ,T ]. а {V ( t ) , t G [0. T ] } - стационарный центрированный гауссов случайный процесс второго порядка, непрерывный в среднем квадратическом, V : R ^ R. Его автоковариационная функция вычисляется по формуле

C v ( т ) = E [V ( t + т ) V ( t )] =

/

R

e i “^T S v ( w ) dw,

где спектральная плотность S v ( w ) определяется следующим выражением:

S v ( w ) — aV/ ( bV + w^ ) ,   av >  0 ,   bv >  0 ,

E [ ... ] - оператор математического ожидания.

Пусть av - среднее квадратичное отклонение процесса. V ( t ) при лтобом t G [0 ,T ].

такое что aV = Cv(0) = J Sv(w) dw.

Поэтому случайный процесс {V ( t ) ,t G [0 ,T ] } может быть представлен как (стационарное)

решение СДУ Ито dV(t) = -bv V(t) dt + av dW(t), t G [0,T],

(2-6)

co случайными начальным условием V (0) = V o, г де W - скалярный винеровский случайный процесс, и где распределение случайной величины V - инвариантная мера P v, которая является гауссовой вероятностной мерой с нулевым средним и средним квадратичным отклонением av-

Структура ядра уо(t,t; Q) была выбрана в форме до(t,T; Q) = Kо(dt) {1 -

- ^ ре(et) [1 - ехр{-T^t_}]} и основана на модели из [9]. В правой части формулы для 7о(t,T; Q) присутствуют: et - температура механического компонента, Kо(et) > 0 - начальная упругая характеристика, зависящая от температуры, Ti(dt) -большое время релаксации, р 1(et) - безразмерный параметр, не зависящий от 0t, T2(dt) - малое время релаксации, р2(0t) - безразмерный параметр, зависящий от 0t, причем в соотношения для перечисленных величин входят компоненты вектора случайных параметров Q

Сформулированную модель динамической системы можно представить в виде системы СИДУ следующего вида:

X ( t ) = A( t ; Q ) X ( t ) +

+ [ B( t,T ; Q ) X ( т ) dT +     (2.7)

J1 0

+ G( t ; Q ) [ V ( t )+ v ( t )] , t G ( t о ,T ] , X ( t о) = X ^о ,            (2.8)

где X(t) = {Xi(t),X2(t),...,Xn(t)}T - вектор состояния; Xо - гауссов случайный вектор со значениями в Rri, определяющий на чальное состояние, mxо = E Xо] ,

CXXо = E [(Xо - mxо) (Xо - mxо)T] ; вход V(t) = {V1(t),V2(t),...,Vm(t)}T. t G [tо, + то) - векторный случайный процесс, который статистически независим от Xо и удовлетворяет векторному линейному СДУ Ито dV (t )= H V (t) dt + O dW (t), t>t о (2.9) co случайным начальным условием V (tо) = Vо. В уравиешш (2.9) H G M(Rm^m) 11 O G M(Rmxr) - детерминированные матрицы (M - множество действительных матриц соответствующей размерности); W(t) = {Wi(t),W2(t),...,Wr(t)}T - г-мерныи винеровский случайный процесс с независимыми компонентами такой, что обобщенная производная по времени t, обозначаемая через W(t) = {W1(t),W2(t),...,Wr(t)}T. еств rave-совский белый шум с независимыми компонентами,

E [ W ( t )]=0 ,

E [W(t) WT (t')] = 2 n E 6(t - t'), где 6 - дельта-функтщя Дирака. E - единичная матрица, V0 - начальный вектор, представляющий собой центрированную гауссову случайную величину со значениями в Rm. Предполагается, что плотность вероятности Vо - гауссово стационарное распределение, ассоциированное с уравнением (2.9), причем среднее mvо = £[Vо] = 0. а ковариационная матрица Cvvо = £ Vо V^]. Кроме того, матрицы H ii O таковы, что V - случайный процесс второго порядка. Следовательно. {V(t),t ^ tо} - статщоиар-ный центрированный непрерывный в среднем квадратическом гауссовский случайный процесс, для которого mv (t) = £ [ V (t)] = mv о = 0,

C vv ( t -1' ) = £ [ V ( t ) V ^T ( t' )] ,

C vv (0) = C vv о .

В уравнении (2.7) Q = {Q 1 ,Q 2 , ...,Qs}^T - векторная случайная величина, возможные 'значения которой q = {q 1 ,q2,...,q_s}^T определены в R s , причем для любых фиксированных t 11 Т- таких что t о < т С t С T- A( t ; q ) и B( t, т ; q ) - детерминированные матрицы в R ^nxn _; G( t ; q ) - детерминированная матрица в R ^nxm, Эти матрицы и вектор зависят от случайного вектора Q со значениями в B q С R s и известным вероятностным распределением P q ( d q ). Для всех q из B q матрицы-функции A( t ; q ). B( t,T ; q ). G( t ; q ) предполагаются дифференцируемыми необходимое число раз. Дополнительно предполагается. ЧТО v ( t ) = {v 1( t ) ,v 2 ( t ) ,...,v_m ( t ) }^T - заданная детерминированная непрерывная функция со значениями в R ^m. Обозначение X Q показывает, что поведение случайного процесса. X зависит от реализаций q случайного вектора Q.

Учитывая, что n = 4. m = 1. t о = 0 ii v ( t ) = 0, можно заметить, что уравнения (2.4), (2.5) и (2.3) могут быть записаны в виде (2.7), (2.8), причем

A(t; Q) = {aj}, a31 = a42 = 1, a 11 = - 2 ^ц1 /2 ш i, a 12 = 2 ^ц1 /2 ш 1, a 13 = —ш2 — 7о(t^t; Q), a 14 = —ш2 , a21 =2 €ш2, a22 = — 2 €ш2, a 23 = ш 2, a 24 = —ш 2, aij = 0 при остальпых i u j;

B(t,T; Q ) = {bij},    b 13 = —y(t,T; Q), bij = 0 при осталвных in j;

G( t ; Q ) = {—g ( t ) , —g ( t ) , 0 , 0 }^T ;

X ( t ) = {U 1( t ) ,U 2 ( t ) ,U 1( t ) ,U 2( t ) }^T ;

X ^о = { 0 , 0 , 0 , 0 }^T.

Кроме того, уравнение (2.6) записано в форме уравнений (2.9) для случая m = 1, t о = 0. H = —bv 11 O = av-

Задача исследования состоит в получении вероятностных характеристик вектора состояния X ( t ).

Для всех непустых и неупорядоченных точечных подмножеств t = {t 1 ,t 2 , •••,t_in} отрезка [ t о ,T ] in-мерное условное распределение случайного вектора X Q = { X ^Q ( 1 1),

X Q ( t)}^T при заданной реализации q вектора Q является гауссовым, определяемым вектором средних m X ( t ) и ковариационной матрицей C Xx ( t ). Определим векторную функцию математического ожидания и матрицу ковариационных функций векторного случайного процесса X ( t ) и то же для случайного процесса X ^Q ( t ) при данном Q, а также все взаимные ковариационные функции X ( t ) и X ^Q ( t ) с вектором возмущения V ( t ):

m x ( t ) = £ [ X ( t )] ,     m X ( t ) = £ [ X ^Q ( t )] ,

^C XX ⁽ t 1 ,t 2) = ^£ [ ^{X (} t 1) ^{XT (} t 2)] ^—

• —    m x ( 1 1) m X ( 1 2) ,

C Xx ( 1 1 ,t 2)= £ [ X ^Q ( 1 1) X ^QT(1 2)] —

• —    m X ( 1 1) m X^T ( 1 2) ,

C xv ( 1 1 ,t 2) = £ [ X ( 1 1) V ^T ( 1 2)] ,

C Xv ( 1 1 ,t2 )= £ ^[ X ^Q ( 1 1) V ^T ( 12 )] ,

C vx ( 1 1 ,t 2) = £ ^[ V ( 1 1) X ^T ( 1 2)] ,

C Qx ( 1 1 ,t2 )= £ ^[ V ( 1 1) X ^QT(1 2)] •

В последних соотношениях для фиксированного Q = q из Bq условные моментные функции mX(t). CXx(11 ,t2). CXv(11 ,t2) II Cvx (11 ,t2) далее будем обозначать mx (t; q), Cxx(t 1 , t2;q)■ Cxv(t 1 , t2;q) 11 Cvv(t 1 ,t2;q) соответственно. Отсюда безусловные векторные функции математического ожидания и матрицы ковариационных функций векторного случайного процесса X(t) и взаимных ковариационных функций можно оп- ределить по формулам:

m x ( t ) = Bo m x ( t ; q ) P Q ( d q ) ,

Q

C xx ⁽ t i ,t 2) = B _Q C xx ⁽ t i ,t 2; q ) P q ⁽ d q ) ,

C xv ⁽ t i , t 2) = B Cxv ⁽ t i , t 2; q ) P q ⁽ d q ) ,

Q

C vx ⁽ t 1 , t 2) = Bo C vv ⁽ t 1 ,t 2; q )^P q ⁽ d q ) .

Q

Принимая во внимание введенные определения и обозначения, несложно увидеть,

Тогда матрица условных ковариационных функций этого процесса определится следующим соотношением:

(P ^q _t \ _ rC xx ⁽ t 1 ,t2) Cxv ⁽ t ¹ ,t ²я C^xx ( t ¹ ,t 2) = ^C Qx ₍ 1 1 ,t 2 ) C Qv ₍ 1 1 ,t 2)]

что решение поставленной задачи заключается в создании схемы для вычисления век-

—

—

торной функции математических ожиданий m x ( t ) ^и матрицы ковариационных функ-пий C xx ( 1 1 ,t ₂) для лтобых t. 11. 12 E ( 1 0 ,T ].

а сам процесс ZQ (t) будет решением мы СИДЕ dZQ (t) = [A(t; Q) ZQ (t) +

+ 1 B( t,T ; Q ) Z ^Q ( T ) dr ] dt +

+ (O d W ( t ) , 1 0 <  t ' <  T

систе-

(3.2)

(3.3)

(3.4)

Такая схема должна состоять из двух этапов, соответствующих введенным выше ра

—

—

венствам: 1) вычисление условных первых и вторых моментных функций случайного

co случайным начальным условием

Z ^Q ( t ' ) = Z ^Q ( t ' ) - m x ( t ' ) ,

(3.5)

процесса. X Q при за,данном Q 2) вычисление безусловных первых и вторых моментных функций того же процесса.

1_

3. Модификация метода аппроксимации функции Грина

В данном разделе представлены основные соотношения, адаптирующие метод ап-

—

проксимации функции Грина, который был разработан в [1], на более широкий класс

СИДУ, чем в предыдущих исследованиях, и учитывающие возможность применения численно-аналитических и параллельных расчетов.

—

_

где

—

A( t ; Q ) =

B( t, t ; Q ) =

'A( t ; Q ) G( t ; Q )

H

,

[^B( tT Q ’ 0] , —-[O] -

Отсюда для условной ковариационной функции

C^Qxx ( 1 1 ,t 2)= E Z ^Q ( 1 1) Z ^QT(1 2)]

при 'заданном C xx ( t ' ,t ' ) из (3.2) получены следующие уравнения ( t о <  t ' < t <  T):

^d C zz ( t,t ' )= A( t ; Q ) C Qz ( t,t ' )+

• 3.1.    Уравнения для условных первых моментных функций

Применение оператора условного математического ожидания (при заданном Q ) к обеим частям уравнений (2.7) и (2.8) дает:

m x ( t ) = A( t ; Q ) m x ( t ) +

+ / B( t,T ; Q ) m x ( t ) dT +

J f

+ G( t ; Q ) v ( t ) , 1 ₀<  t ' <  T, (3.1)

^mX ⁽ t ' ) = ^mX ' ,

m X (t ' )= m x о , t ' = t о .

+ [ B( ^t,T ; ^Q ) C Qz ^{( T,t} ' ) dr t'

dt C Qz ⁽ t, t ) = ^A( t ^{; Q} ) C Zz ⁽ t, t ⁾⁺ + [A( t ; Q ) C Q_z ( t, t )] ^T +2 n (O (O ^T + + £ [B( t,r ; Q ) C Qz ( r,t )+

(3.6)

+ {B( t,r ; Q ) C Q_z ( r,t )} ^T] dr. (3.7) Уравнения (3.6), (3.7) должны решаться с учетом начальных условий

Для построения уравнения относительно C xx ( 1 1 ,t 2) вектор состояния системы (2.7) должен быть расширен до нового центрированного случайного вектора

Z ^Q ( t ) =col( X ^Q ( t ) - m x ( t ) , V ( t )) .

CQz ⁽ t в = CQz, C Qz ' = C Qz ⁽ t 0 ,t 0) = C zz 0 = [0 C _vv J

ДЛЯ t ' = 1 0-

• 3.2.    Приближенное вычисление условных первых моментных функций

Предположим, что необходимо решить систему детерминированных ИДУ

Z ( t ) = A ( t ) Z ( t ) + ^ft B ( t, т ) Z ( т ) dт + t'

+ F(t),     tо С t' < t, с начальными условиями

Z (t ' ) = Z ' , Z ' = Z о ч.тя t ' = t о .

Решение уравнений (3.8) и (3.9) для может быть записано так [10]:

(3.8)

(3.9) t ' < t

Z ( t )= R( t,t ' ) Z ' + [ R( t,т ) F ( т ) dт, Jt'

(3.10) где R( s,s о) - матрица-функция Грина, ассоциированная с уравнением (3.8) и являющаяся решением уравнения

∂

R( s, s о) = A ( s ) R( s, s о) +

∂s

+ ! B ( ',т ) R( т,' о) dт, s о < s, (3.11) s 0

R( s о ,s о) = E ,

В отличие от [10] итерационная процедура, описанная в [1], позволяет представить R( s, s о) без использования операции интегрирования в следующей форме:

R( s,s о)= E + ^g RAy°l 4 ,  (42)

I =1

R £ ( s,s о) = dL-^ R( s,s о) , s * = s — s о .

Используя этот подход, коэффициенты ряда

Тейлора в равенстве (3.12) могут бытв по. лучены последовательным дифференциро

I-

I-

ванием обеих частей уравнения (3.11) по t.

Ограничиваясь на практике L-й ной, из равенства (3.12) можно что производно лучить,

s i   (3.13)

R[ L )( ',' «) = E + E R ' ."

£ =1

с точностью O [( s — s о) ^L ] (cm. [11]).

При применении построенного представления для R[l] (s, sо) вектор-функция условного математического ожидания mX (t) выражается соотношением mX (t) = R[m] (t,t')] mX' +

=

+ f R^[ m ^]( t,T ) F ( т ) dт, t'

(3.14)

где F ( т ) = G( т ; Q ) v ( т ), а матрица-функция Грина R (s,s о), ассоциированная с вектором m X ( t ). записыв;тется как R^[ m ^]( s,s о) и вычисляется из уравнения (3.11) и равенства (3.13) при A ( t ) = A( t ; Q ). B ( t,т ) = B( t,r ; Q ). В свою очередь соотношения для вычисления матриц условных ковариационных функций будут выглядеть так:

C Qz ( t,t ' )= R ^[ C ^]( t,t ' )] C Qy ( t ' ,t ' ) ,

^C Zz ^{( t} , ^{t )]} =                               (3-13)

= R^[ C ^]( t, t ' )] C QY ( t ' , t ' ) R^[ C ^{] T} ( t, t ' ) +

+ 2 n f R^[ C ^]( t,т ) (O {R^[ c ^]( t,т ) (O} ^T dт, t'

t о С t ' < t С T.

Здесь матрица-функция Грина R (s,s о), ассоциированная с матрицей C Qz ( t,t ' ), запи-

—

сывается как R^[ C ^]( s,s о) и вычисляется из уравнения (3.11) и равенства (3.13) при A ( t )

_

—

= A( t ; Q ). B ( t,т ) = B( t,т ; Q ).

Введем временную сетку tо = то <т1 < ... < Tk- 1 <тк < ... < TN = T, hk = тк — Tk- 1, k = 1 ,N, max hk = h* ^ 1. Адаптируем полученные вышe соотношения для условных первых и вторых моментных функций в непрерывном времени для расчета этих же функций в узлах сетки:

• ^m Xk_ ^_ ^mX ^{( т} к ) CQzv = CQz ^{( т} к, ^т » )> k^ v = 1 , N . Тогда численная аппроксимация вектор-функции условного математического ожидания m X ( t ) определяется равенством

• ^m Xk = ^R [JC ^тк ,^Tk- 1) ^m x,k- 1 ⁺

τ k

+ /   R[ m ( Tk,т ) G( т ; Q ) v ( т ) dт,

J Tk- 1

k = 1 , 2 ,...,N,           (3.1G)

m X _о = m X о .

Интеграл в (3.16) может быть вычислен, например, с помощью метода Симпсона [12]. Подобным образом могут быть вычислены условные матрицы ковариационных функций:

с Q   = 91! C](т т AC Q

Czzvk R[L] ('v, 'v- 1) Czz,v-1 ,k, k = 0, 1 ,...,N — 1, v = k + 1 ,k + 2 ,...,N, с Q          [ C] C Q              [ C] T -i-

^C zzkk ^{= R} [ L ] k ^C zz,k - 1 ,k - 1 ^R [ L ] k ⁺ τ k

+2 п I R[ c ’( Tk,т ) (O {R[ C ]^]( Tk,т ) (O} ^Tdт,

^T k - 1

m[ C ] —ml Cт, М л _ 1 о т\г R[ L ] k — R[ L ] ^{( T}k^,Tk — 1) , k — ¹ , ² , ■■■, N,

C Qz 00 ^— C ZZ 0 ■

4.    Детали алгоритмов и обзор результатов расчетов

Прежде всего отметим, что выбранное для проводившихся расчетов случайное возмущение не изменяет математических ожиданий случайных функций Ui ( t ), которые в начальный момент времени равны нулю. Поэтому эти математические ожидания методом функций Грина (GFM) не вычислялись, хотя схема их расчета и была реализована.

Вычисления проводились с помощью программ на языке Intel Fortran в среде Microsoft Visual Studio. Для прямого статистического моделирования системы СИДУ использовалась полунеявная модификация метода Эйлера-Маруямы (созданная для численного интегрирования СДУ [13]) следующего вида:

Э,          ^{h 0} А.  Э. А.      Э

Zk+1 ,p — 2 Akkp Zkp + Ak+1 ,p Zk+1 ,p) + h2

+"2" (B k +1 ,kp Z kp + B k +1 ,k +1 ,p Z k +1 ,p) +

+ O А W kp,        (4.1)

k — 1, 2 ,...,N,   p — 1, 2 ,...,M, где h0 — T/N - постоянная величина, p -номер моделирования,

Z kp — Z ^{[ p ]} ( tk ) ,

А W kp — W ^{[ p ]} ( tk +1) - W ^{[ p ]} ( tk ) , A kp — A( tk ; q p ) , B kp — B( tk ; q p ) ■

Схема, определенная равенством (4.1), требует разрешения системы линейных алгебраических уравнений для получения значений последовательности Z k +1 ,p во времени. Необходимое обращение матриц было реализовано с помощью метода исключения Гаусса.

Хорошо известно, что реализации метода Монте-Карло (ММС) требуют значительного количества случайных или псевдослучайных чисел (ПСЧ) с различными распределениями. Наш процесс получения выборок для случайного вектора Q был основан на встроенном системном датчике ПСЧ, равномерно распределенных на (0,1), и реализованной функции, дающей нормальные гауссовы ПСЧ по методу Марсальи-Брея [2].

Для векторного стохастического процесса Y пошаговые оценки для векторных фун кций математических ожиданий и матрич ных ковариационных функций выглядели так:

₁ M -

™ Zk ^— M ^Z kp, p =1

M tZkij — M   Zkpi Zkpj — mZki mZkjm p=1

где C z ( t )- матрица с ксшпоиеитами Zzij ( t ) —

C zzj ( t,t )■ i,j € { 1 , 2 , 3 , 4 }.

Реализация метода функций Грина сос тояла из двух этапов. На первом выполня лись аналитические выкладки для получения выражений для R?(s0,s0). I = {1- 2. 3. 4}, удобных для дальнейших расчетов. Эти символьные расчеты, включающие дифференцирование, подстановки, приведения подобных и т.д., были выполнены в пакете Ма-thematica. Самый сложный символьный под этап состоял из смешанных ручных и компьютерных преобразований для результатов дифференцирования функций 70 (t,T; Q) и Э(t, т; Q) из-за их сложной структуры. Этот подэтап требовался для достижения эффективности вычислений в программе на языке Fortran. Заметим, что по сравнению с использовавшейся компьютерная автоматическая оптимизированная генерация соответствующего ^оНгап-фрагмента пакетом Maple оказалась малопригодной для расчетов из-за потери структуры выражений.

На втором этапе численные расчеты, как и выше, выполнялись в среде Microsoft Visual Studio с помощью разработанной Intel For iran-программы. В этой программе сначала формировались неизменяемые части матриц до основных вычислений и затем к ним добавлялись переменные части. Целью этого было сократить время расчетов и для ММС, и для GFM.

Расчет выборок Q и статистическая обработка были подобны описанным выше. Схема вычислений оценок C( 1 1 ,t 2; Q ) состоит из трех основных циклов:

• •    по моделированиям p = 1, 2, ..., M',

• •    для расчета условных одноточечных функций C QZ ( т_к +1 ,Tk +1; q_p ), k = 0 ,N - 1;

• •    для расчета условных двухточечных функций C Q_Z ( Tk +1 ,т_е ; q_p ), k < £ <  N.

Учитывая структуру GFM, для реализации алгоритма оказалось возможным использовать встроенные матричные операции. Для вычисления интегралов применялся метод Симпсона с переменным числом J интервалов разбиения промежутка интегрирования.

Параметры, определяющие точность результатов, были установлены так:

• •    T = 1200:

• •    h о = 0.01, N = 120000 - для основных расчетов;

• •    h о = 0.005, N = 240000 - для контрольных расчетов;

• •    значения M варьировались от 1000 до 60000 на разных стадиях;

• •    J =Sii L = 1 для GFM.

• 5.    Применение параллельных вычислений для ускорения расчетов

В связи с направленностью работы на вычислительные аспекты задачи ниже приведено минимальное количество рисунков.

На рис. 2, 3 приведены кривые, полученные GFM и соответствующие функциям ковариации для различных уровней параметров неопределенности (изменение номера от 1 до 4 характеризует увеличение рассеивания). Для проверки результатов расчетов вычисления производились и с уменьшенными вдвое шагами сетки, но результаты, полученные для различных шагов, различались несущественно. Рис. 4 демонстрирует хаотические режимы для выбранных ковариаций в начале процесса.

Полученные результаты, включающие и сглаживание выборочных распределений, наглядно демонстрируют эффекты нелинейного вхождения неопределенностей, а следовательно, негауссовость отклика линейной динамической системы при гауссовом возбуждении, но с неопределенностью в параметрах модели.

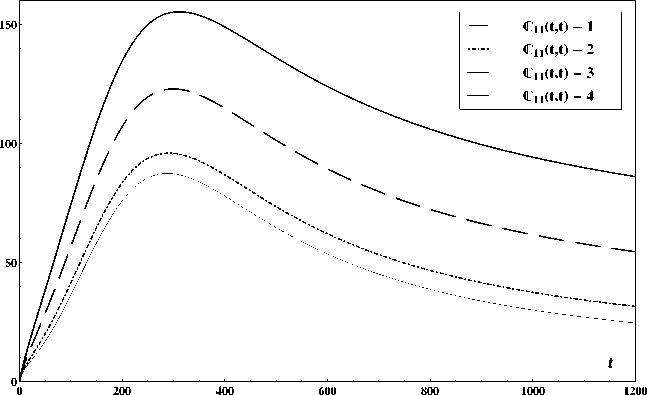
Рис. 2

При решении рассматриваемой задачи необходимо произвести многократное моделирование СИДУ (число таких моделирований при решении практических задач стохастической механики исчисляется сотнями тысяч [14]) в рамках выбранной полунеяв-ной схемы Эйлера-Маруямы. Вследствие того, что все моделирования являются независимыми, можно разделить вычисления так, что будет использоваться сколь угодно большое количество вычислительных узлов (процессов).

Общепринятым стандартом для организации параллельных вычислений является Message Passing Interface (MPIf С его помощью можно создавать масштабируемые решения для систем с распределенной памятью.

Для использования возможностей MPI в изначально разработанный однопоточный алгоритм интегрирования были внесены из-

0.008

0.006

0.004

0.002

0.000

0.04

0.02

0.00

- 0.02

- 0.04

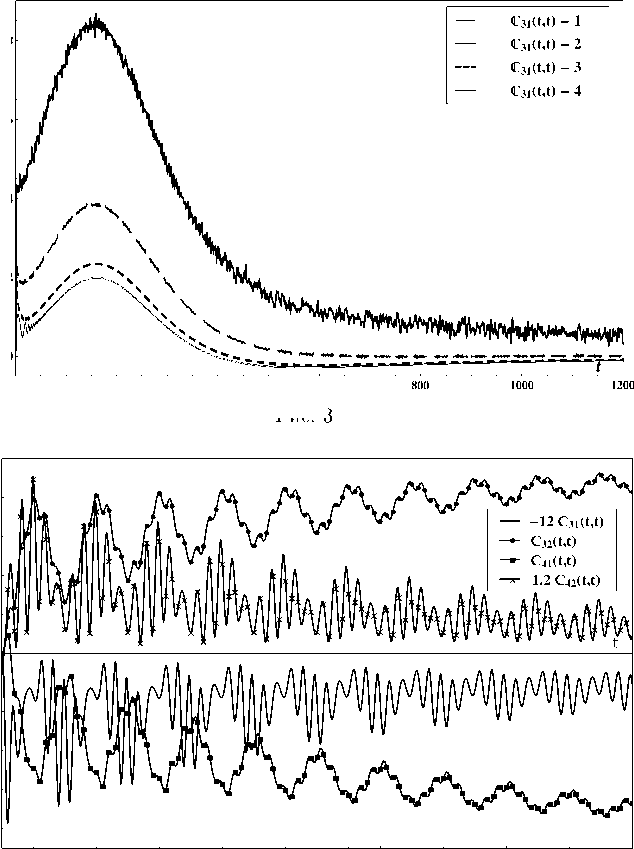
Рис. 4

Рис. 3

менения. Процесс с rank = 0 (root) был выбран управляющим. На этапе работы MPI этот процесс формирует 2 буфера с параметрами, которые необходимо отправить вычис-лителвным узлам с rank = 1, 2, ..., size—1. Отправка и получение сообщений осуществлялись с помощью блокирующей передачи: MPI_SEND (buffer, sizeofmessage, datatype, destination, tag, comm, ierr);

MPI_RECV (buffer, sizeofmessage, datatype, source, tag, comm, status, ierr)

где buffer - пересылаемое сообщение (массив) с одним или несколькими параметрами; sizeofmessage - размер массива; datatype -тип данных массива; destination - номер процесса, которому передается сообщение;

source - номер процесса, от которого ожидается сообщение; comm - константа, равная внутреннему значению MPI МР1_СОММ_ WORLD; tag - тег; в ierr MPI записывает внутреннюю константу ошибки, которая произошла во время передачи сообщения.

Каждому из процессов с rank = 1, 2, ..., size — 1 в качестве одного из параметров передается количество моделирований, которые ему необходимо провести. Это количество вычисляется по следующей формуле:

modNumber 4 Proc = NSamples/(size — 1), где modNumber4Proc - количество моделирований для каждого процесса, NSamples -общее количество моделирований, size - количество процессов, которые доступны MPI. Каждый из процессов с rank = 1, 2, ..., size —

• 1    осуществляет необходимое количество моделирований, после чего отправляет результаты корневому процессу с rank = 0. После выполнения вычислений корневой процесс поочередно суммирует результаты моделирований от каждого процесса.

Многопоточный алгоритм тестировался в среде ОС Microsoft Windows 8.1 х64, установленной на стационарный компьютер с процессором Intel Core 2 Quad Q6600 (тактовая частота 3.17 ГГц) и оперативной памятью объемом 4 ГБ. Для сборки Fortran MPI-программы использовался компилятор Intel Composer ХЕ 2011 х64 и компоновщик Microsoft Visual С 7+ 2010 х64. В качестве реализации интерфейса MPI был выбран MPICHх86_64 версии 2 (сборка Jayesh Krishna). В настройках компилятора было изменено значение флага оптимизации Maximize Speed plus Higher LevelOptimizations (/03).

Для тестирования эффективности параллельной реализации алгоритма были выбраны следующие параметры (общее модельное время процесса 1200 с):

Параметр	Значение
Общее количество моделирований	60000
Шаг	0.001
Количество шагов	1200000

Затраты времени на расчеты измерялись с помощью следующих команд MPI:

startTime = MPI_WTIME() endTime = MPI_WTIME() calcTime = endTime - startTime и составили:

Количество вычисляющих узлов	Время вычислений (ч)
1	24.8
3	9.5

Из приведенных данных следует, что по сравнению с однопоточной реализацией при количестве вычисляющих процессов, равных трем, удалось получить ускорение вы-вычислений примерно в 2,6 раза.

Заключение

По результатам расчетов были сделаны следующие выводы:

• -    применение параллельных вычислений при решении задач стохастической вязкоупругой механики является эффективным способом ускорения расчетов;

• -    системы аналитических вычислений имеют необходимый функционал для организации параллельных вычислений как в автоматическом, так и ручном режиме. Но при этом имеются ограничения по памяти, а скорость вычислений заметно уступает программам, написанным с использованием языков С/C++ и Fortran под конкретную архитектуру процессоров.

Поэтому перспективным способом для организации решения задач стохастической вязкоупругой механики с использованием параллельных вычислений является следующий подход:

• -    с помощью систем аналитических вычислений, например пакета Mathematics, производятся все необходимые аналитические вычисления, а далее с помощью встроенных команд генерируются необходимые соотношения для расчетов на языках С или Fortran

• -    в сгенерированный код вносятся необходимые изменения для использования таких технологий, как ОрепМР или MPI,

• -    измененный код компилируется под конкретную архитектуру, что, например при использовании MPI API, дает возможность получать гибкие масштабируемые С/Fortran "вычислители" (или "решатели", от англ. solvers) для использования на кластерах.