Параметрический α-уровневый метод λ-продолжения для задачи нечеткого линейного программирования
Автор: Шаталова А.Ю., Лебедев К.А.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Управляемые системы и методы оптимизации
Статья в выпуске: 1, 2018 года.
Бесплатный доступ
В статье рассмотрен известный метод четырех задач нечеткого линейного программирования, который обобщен до параметрического α -уровневого метода λ -продолжения. Предложенный метод позволяет сократить количество рассмотренных случаев с четырех до двух, позволяет получать дополнительные решения на подмножествах квадрата α - λ. Преимущества предложенного подхода состоят в том, что они включают в себя четыре описанные ранее задачи как частные случаи. Метод позволяет получать более общие и гибкие решения, дает возможность влиять на свойства линейной задачи оптимизации: меру принадлежности, чувствительность, устойчивость. В статье также рассмотрен численный пример, показывающий работу нового метода и реализованный в программной среде MathCAD.
Нечеткое линейное программирование, оптимизационные задачи, параметрическое линейное программирование с нечеткими данными, принцип расширения, метод продолжения, нечеткие множества, нечеткая логика
Короткий адрес: https://sciup.org/14835246
IDR: 14835246 | УДК: 519.688 | DOI: 10.18101/2304-5728-2018-1-34-51
Текст научной статьи Параметрический α-уровневый метод λ-продолжения для задачи нечеткого линейного программирования
На практике требование детерминированности входных данных является неоправданным упрощением реальности. Так, часто входящие параметры характеризуются множеством факторов неопределенности. Теория нечетких множеств позволяет более детально интерпретировать результаты наблюдений, полученных опытным путем, т. к. дает исследователю инструменты для анализа неоднородных и недостаточных выборок, которые классическая теория вероятности законно игнорирует [3].
При разработке инструментария для нечеткого подхода используются различные методы. Задачи, в которых нечетко описано множество допустимых выборов (альтернатив) и (или) функции полезности, принимают вид задач нечеткого математического программирования [1]. Существует два различных подхода к их решению:
-
1) подход Беллмана — Заде — задача формулируется как задача выполнения нечеткой цели при нечетких ограничениях, причем решение задается пересечением нечетких множеств цели и ограничений [2].
-
2) выбираются эффективные альтернативы в понимании Парето [1].
Необходимо отметить, что нахождение полного решения некоторых задач нечеткого линейного программирования довольно трудоемко и требует больших вычислительных затрат, поэтому на практике применяется второй подход. В этих случаях ищут так называемое «компромиссное» решение, для определения которого предложены различные функции предпочтения, которые преобразуют бесконечное множество целевых функций в единственную компромиссную целевую функцию [3].
В работах [3; 4] представлены методы линейной оптимизации с нечеткими данными, позволяющие находить оптимальные решения задач линейного программирования с коэффициентами в виде нечетких чисел путем сведения их к параметрическим задачам линейного программирования.
В [3] задачи рассматривались с коэффициентами в виде нечетких треугольных чисел, имеющих левую (L), правую (R) стороны и середину (C), поэтому в линейной задаче выражения для целевой функции и ограничений могут быть записаны в форме левой (L) или правой (R) стороны (рис. 1) c использованием среднего значения (C) [5].
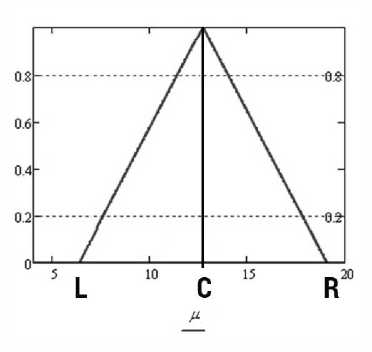
Рис. 1. Треугольное число a = ( aL , aC , aR )
При возникновении бинарного отношения можно установить следующие способы сравнения:
a = ( aL , aC , aR ), b = ( bL , bC , bR )
aC < bC — сравнение, аналогичное сравнению действительных чисел; aL < bR — «слабое» отношение;
aR < bL — «сильное» отношение. Данные обозначения вводятся в [3].
Таким образом, возникает два расширения бинарного отношения неравенства «меньше или равно» ( ≤ ): «слабое» — A m ≤ in B , ( AL ≤ BR ) и «сильное» — A m ≤ ax B , ( AR ≤ BL ) , где А и В — линейные выражения относительно неизвестных с нечеткими треугольными коэффициентами (в частности, треугольное число). Так как задача линейного программирования содержит отношение неравенства (или равенства) в ограничениях, а целевая функция может быть записана в форме левой ( L ) или правой ( R ) стороны коэффициентов, то метод задает четыре связанные между собой параметрические задачи. В статье [5] рассмотрен пример применения данного подхода к экономической задаче оптимального инвестирования.
В данной статье, в отличие от [3; 5; 6], предлагается усовершенствовать метод: ввести дополнительный параметр λ ∈ [0,1] , и вместо четырех связанных между собой задач с a ∈ [0,1] рассматривать две, но с двумя параметрами a , λ ∈ [0,1] . Параметр λ назовем параметром «гибкости», а сам метод — параметрическим a -уровневым методом λ -продолжения задачи нечеткого линейного программирования.
Построена модель и создана программа с помощью пакета MathCAD, позволяющая решить задачу линейной оптимизации при нечетких коэффициентах в ограничениях и целевой функции. Параметрический a -уровневый метод λ -продолжения задачи нечеткого линейного программирования позволяет получить решение задачи при различных значениях a , λ ∈ [0,1] .
2. Метод параметризации задачи
В работе [3] приведен параметрический a -уровневый метод задачи нечеткого линейного программирования с использованием a -эффективного решения, где значение a является уровнем эффективности. Метод позволяет для различных значений a ∈ [0,1] и четырех разных задач с использованием «слабого» — A m ≤ n B и
«сильного» — A ≤ B отношений построить семейство задач, связанное с классическим линейным программированием.
Параметр a ∈ [0,1] имеет значения в отрезке от 0 до 1 (a∈[0,1]). Используя метод погружения задачи в семейство задач с параметром продолжения λ∈ [0,1] , можно показать, что методы, изложенные в [3], позволяют решать задачи только при λ = 0 или λ = 1, что в системе координат (рис. 2а) отображается двумя отрезками LR-RL на верхней и нижней сторонах квадрата, а другая область квадрата недоступна. Предлагаемый здесь метод позволяет рассматривать точки и в середине области квадрата, например, со значением a = 0,7 и X = 0,5 (рис. 2б), в промежутке между слабым и сильным отношениями.
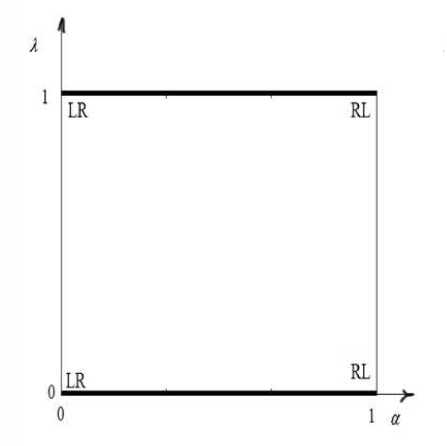
Рис. 2а. Вид области определения параметров a = 0; 1, X = 0; 1
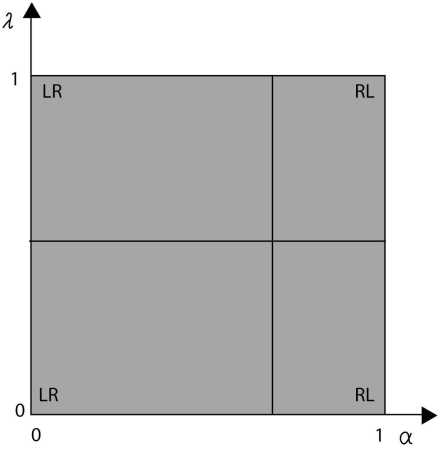
Рис. 2б. Вид области определения параметров a е (0; 1), X = (0; 1)
Задача линейного программирования с нечеткими данными имеет вид
[3]:
f (x) = ( c , x ) ^ min(max), x e X = { x e E n : Ax < b}, (1)
где с — вектор с элементами в виде нечетких треугольных чисел ci (i = 1, n), A — матрица, состоящая из нечетких треугольных чисел aj = (а/, ajC, ajR) (i = 1,m, j = 1, n) с функциями принадлежности вида t — aj a-j — t на вещественном носителе R,
ba, (t) = max{0,min(—----Г;—----c )}
j aj - aj aj - aj b — вектор с элементами в виде нечетких треугольных чисел bi (i = 1, m) со своими функциями принадлежности на носителе R.
Обозначим через LR лево-право-стороннее: ( Ax) a < b R ; а через RL право-лево-стороннее отношение: ( Ax) R < b R , где AL , A R , bL , bR вычисляются по формулам, вывод которых очевиден из рис. 3 [3]:
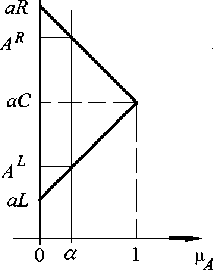
Рис. 3. Построение функций принадлежности треугольного числа a = ( aL , aC , aR )
AL = aL + ( aC — aL ) a ,
A R = aR — ( aR — aC) a , (2)
bL = bL + (bC — bL)a , bR = bR — (bR — bC)a , a = (aL, aC, aR), b = (bL,bC,bL) — треугольные числа (нижние индексы опущены). Параметр ae[0,1] можно трактовать как «показатель эффективности», т. к. при a = 1 коэффициенты принимают значения действительных чисел, а при a = 0 — все значения из сечения А0 треугольного числа.
Коэффициенты целевой функции также представляются в виде нечетких чисел вида: c = ( cL,cC, cR ).
Из равенств (2) видно, что при а е [0,1] коэффициенты ограничений принимают значения на некотором множестве в зависимости от выбранного а и при ( c T x) a ^ min или ( c T x) R ^ min задача линейного программирования в этом случае делится на четыре возможных варианта (табл. 1) [3]. Понятно, что задачу можно рассматривать и на максимум (max) целевой функции, что не приведет к принципиальным отличиям.
Таблица 1
|
Вид целевой функции |
Вид ограничений |
|
( c T x ) L ^ min(max) |
( Ax ) L < b R , (1 задача) |
|
( Ax ) R < b L , (2 задача) |
|
|
( c T x ) R ^ min(max) |
( Ax ) L < b R , (3 задача) |
|
( Ax ) R < b L , (4 задача) |
Данный подход с четырьмя задачами позволяет получить оптимальные решения для четырех случаев (четырехсторонний вариант) на двух сторонах квадрата (рис. 3а). Множество точек во внутренней области квадрата не может быть использовано. Развитие метода заключается в погружении задачи в семейство задач с параметром X , который дает возможность решить задачу и для любой точки квадрата, любого сочетания значений а и X из квадрата [0,1] х [0,1] (рис. 2б). Например, для точки ( a = 0,7, X = 0,5) или серии задач при ( a = 0,7, X е [0,1]) или ( X = 0,5, а е [0,1]) или вообще на любом подмножестве из области квадрата.
Предложим метод погружения исходной проблемы с 4 задачами в семейство задач с параметром продолжения. Запишем ограничения задачи в виде:
X ( Ax)L L + (1 - X ) • ( Ax)R R < X b R + (1 - X ) • b L , где X e [0,1].
При X = 0 получается «сильное» ограничение ( Ax) R < b L , а при X = 1 — «слабое» ( Ax) L < b R . Также и целевая функция получает два случая с X = 0 и X = 1. Параметр X позволяет непрерывно, через промежуточные задачи, переходить от задачи LR ( X = 1) к RL ( X = 0). Этот метод (таблица 2) решения задачи линейного программирования назовем параметрическим а -уровневым методом 1 -продолжения задачи нечеткого линейного программирования.
Таблица 2
|
Вид целевой функции |
Вид ограничений |
|
X ( c T x) a + (1 - X ) • ( c T x) R ^ min(max) |
X ( Ax ) a + (1 - X ) • ( Ax )R R < X bR R + (1 - X ) • ba L |
|
X ( c T x ) R + (1 - X ) • ( c T x) L ^ min(max) |
С помощью выбора X можно оценить уровень влияния факторов отношения LR — RL . Ясно, что, задавая промежуточные значения X в промежутке от нуля до единицы, получим возможность влиять на характеристики задачи: разрешимость, устойчивость, чувствительность к изменению параметров.
3. Пример
Сравним метод четырех задач [3] и предложенный метод на простом примере f (x) = c1 x1 + c2 x2 +1 ^ max , (a1 x1 < b1,
[ a 2 x 2 < b 2 .
Пусть c 1 , c 2 , a 1 , a 2 , b 1 , b 2
треугольные нечеткие числа:
c 1 =(2, 3, 4), c 2 =(1, 2, 3), a 1 =(1, 2, 3), a 2 =(2, 3, 4), b 1 =(11, 12, 13), b 2 =(23, 24, 25). Имеем четыре задачи согласно таблице 1. Все четыре задачи решены в разработанной программе в среде MathCAD для четырех угловых случаев LR, RL (рис. 1., табл. 1), для дискретных значений a = 0; 0,1; 0,4; 0,6; 0,8; 1,0. Выпишем все четыре задачи.
-
1) f a ( x ) = (2 + a ) x 1 + (1 + a ) x 2 + 1 ^ max (4)
(1 + a ) x 1 < (13 - a ), (2 + a ) x 2 < (25 - a ).
-
2) f a ( x ) = (2 + a ) x 1 + (1 + a ) x 2 + 1 ^ max
(3 - a ) x 1 < (11 + a ), (4 - a ) x 2 < (23 + a ).
-
3) f R ( x ) = (4 — a ) x 1 + (3 — a ) x 2 + 1 ^ max (6)
f (1 + a ) x 1 < (13 - a ), [ (2 + a ) x 2 < (25 - a ).
-
4) f R ( x ) = (4 — a ) x 1 + (3 — a ) x 2 + 1 ^ max (7)
f (3 - a ) x 1 < (11 + a ), [ (4 - a ) x 2 < (23 + a ).
Например, при a = 0,9 задача (4) имеет оптимальное значение f L = 35,258 ( x 1 = 6,368, x 2 = 8,31). При a = 0,9 задача (5) имеет оптимальное значение f L = 32,082 ( x 1 = 5,667, x 2 = 7,71). На рис. 4 показаны оптимальные значения f L ( x ) для задач (4) и (5) при изменении a и X = 1.
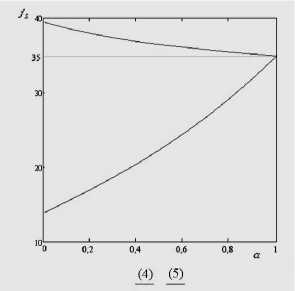
Рис. 4. Изменение оптимальных значений (верхняя кривая — для задачи (4), нижняя — для (5))
Аналогично для задач (6)–(7) построим соответствующие кривые (рис. 5), показывающие изменения оптимальных значений задач (6)–(7) от изменения уровня a , ( X = 1).
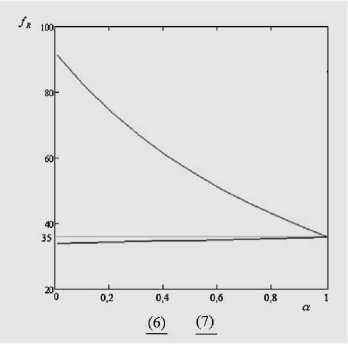
Рис. 5. Изменение оптимальных значений (верхняя кривая — для задачи (6), нижняя — для (7))
Из рис. 4-5 видно, что при a = 1 (все коэффициенты становятся «четкими») значение целевой функции у всех задач одинаково f ( х ) = 35. Также видно, что в задачах (4) и (7), когда для «слабого» отношения целевая функция строится по левосторонней формуле (задача (4)) и для «сильного» отношения — по правосторонней формуле (задача (7)), изменение целевой функции в меньшей степени зависит от а , чем в задачах (5) и (6).
После нахождения оптимального значения целевой функции при заранее заданных экспертом значениях а в задаче параметрического a -уровневого метода необходимо найти функции принадлежности для множества допустимых решений Х и для удовлетворяющего (оптимального) множества X * общей задачи нечеткого линейного программирования [3]. В общем виде это делается с помощью формирования нечеткого вывода [5]. В данном частном случае в задаче (3) необходимо построить функции принадлежности нечетких отношений ограничений, из которых будет формироваться область допустимых значений Х .
Так как в работе используются только треугольные числа, то результатом сложения левых частей ограничений задачи (3) являются также треугольные числа [5]:
g = ~л ( а ) Х 1 + ... + ~ п пхп , i е M ,
L =(gL(х), gC(х), gR (х)), с функциями принадлежности вида:
ц, ( х ) = max{0,min{ t - g ( Х )- , g L ( Х ) t_ }}, t е R , i е M .
L ’,2 ’,2 g C ( х ) - g L ( Х ) g R ( х ) - g C ( х Г
Тогда левые части ограничений задачи (3) имеют вид:
Lx = ( х „ 2 х , , 3 х ’ ), L 2 = (2 х 2 , 3 х 2 , 4 х 2 )
с соответствующими функциями принадлежности: t - x 3 x - t
µL(x)=max{0,min{ 1, 1}}, t∈R, t-2x4x-t
µ L ( x ) = max{0, min{ 2 , 2 }}, t ∈ R .
При a = 0,9, ( λ = 1) задача (4) имеет оптимальные значения x 1 = 6,368, x 2 = 8,31 , функция принадлежности имеет вид:
t - 6,368 19,104 - t
µ(x) =max{0,min{ , }}, t∈R ,(8)
-
L1 6,3686,368
t - 16,62 33,24 - t
µ ( x ) = max{0, min{ , }}, t ∈ R .
L2 8,318,31
Задача (5) при a = 0,9 (λ=1) имеет оптимальные значения x1=5,667, x2=7,71 , и функция принадлежности для левой части будет иметь вид:
t - 5,667 17, 001 - t
µ(x) =max{0,min{ , }}, t∈R,(9)
L1 5,6675,667
µ L 2
t - 15,42 30,84 - t
( x ) = max{0, min{ , }}, t ∈ R .
7,717,71
Строится функция принадлежности нечеткого отношения µ ≤ . На рис. 6 для примера показаны функции принадлежности левой и правой частей первого ограничения задачи (3) для случаев (8) (рис. 6а) и (9) (рис. 6б) соответственно. На рис. 6а показан вид функций принадлежности задачи (3) при a = 0,9, λ = 1 для случая (4) с функциями принадлежности (10). На рис. 6б — для случая (5) с функциями принадлежности (11).
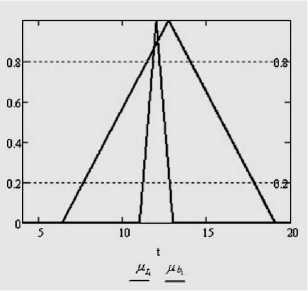
Рис. 6а. Вид функций принадлежности задачи (3) для случая (4)
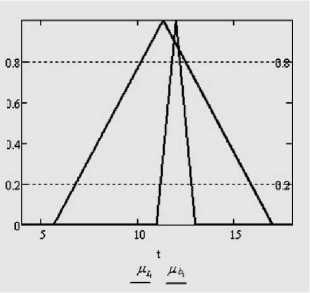
Рис. 6б. Вид функций принадлежности задачи (3) для случая (5)
min max
Функции принадлежности µ≤ нечетких отношений ≤ и ≤ задаются формулами:
µ min( L 1, b 1) = (sup{min{ µ L 1( t ), µ b 1( z )}| t ≤ z }, t , z ∈ R ), (10)
≤
µ min( L 2, b 2) = (sup{min{ µ L 2( t ), µ b 2( z )}| t ≤ z }, t , z ∈ R ).
µ max( L 1, b 1) = (inf{max{1 - µ L 1( t ),1 - µ b 1( z )}| t ≤ z }, t , z ∈ R ), (11) ≤
µ ( L 2, b 2) = (inf{max{1 - µ L ( t ),1 - µ b ( z )}| t ≤ z }, t , z ∈ R ). max 22
где µ b , i = 1,2 — функции принадлежности правых частей ограничений.
На рис. 7 для примера показаны функции принадлежности µ ≤ нечеткого отношения неравенства первого ограничения задачи (3) для случаев (10) и (11) соответственно. На рис. 7а показан вид функций принадлежности µ ≤ нечеткого отношения задачи (3) для первого ограничения при a = 0,9, λ = 1 для случая (4) с функцией принадлежности (10), а на рис. 7б — для случая (5) с функциями принадлежности (11).
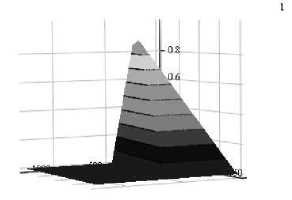
Рис. 7а. µ ≤ ~ нечеткого отношения задачи (3) для случая (4)
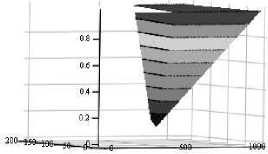
Рис. 7б. ц ~ нечеткого отношения задачи (3) для случая (5)
На рис. 7а sup ц(L1, b1) « 0,83 , а на рис. 7б inf д(L1, b1) « 0,85 . Это ≤≤ показывает, что < можно трактовать как более «слабое» требование ограничения по сравнению с < . Допустимое множество решений Х для задачи (3) имеет функцию принадлежности вида [3]:
Ц х ( x ) = min( ^ < m ,n ( L1 , b 1), ^ < m ,n ( L 2 , b 2 ), ^ ( L 1, b 1), ^ ( L 2 , b 2 )).
Так как целевая функция f — это треугольное число вида f = (2 x + x7 +1; 3 x + 2 x7 +1; 4 x + 3 x7 +1) 12 12 12
с функцией принадлежности вида:
t — 2 x — x7 — 1 4 x + 3 x7 +1 — t ц{ = max{0,min{-----1---2---,—1----2------}}, t e R, x1 + x 2 x1 + x 2
то удовлетворяющее (оптимальное) решение X * имеет функцию принадлежности следующего вида:
Ц Х * ( x ) = min( ^ < m,„ ( L 1 , b 1 ), ^ < m,„ ( L 2 , b 2 ), ^ < max ( L , b 1 ), ^ < max ( L 2 , Ъ 2 ), Ц f ) .
Для задач (4) и (5) ^ f имеет вид соответственно:
ц ( = max{0,min{
t — 22,046 51,402 — t 14,678 ’ 14,678
}}, t e R ,
t — 20,004 46,798 — t -------, , ,---------}}, t e R .
^ f = max{0,min{
13,377 13,377
Значения ^f меняются в зависимости от найденных оптимальных x1 и x2 для каждого a . При требуемом уровне эффективности a = 0,9 (X = 1)
inf цх- ( x ) ~ 0,15, который можно снижать с помощью уменьшения значений a .
Используя таблицу 2, выпишем две задачи для параметрического a -уровневого метода X -продолжения задачи нечеткого линейного программирования. Расширенные условия задачи будут иметь двойной вид:
Л ((2 + a ) x 1 + (1 + a ) x 2 + 1) + (1 - Л )((4 - a ) x 1 + (3 - a ) x 2 + 1) ^ max (12) p(1 + a ) x , + (1 - Л )(3 - a ) x , < Л (13 - a ) + (1 - Л )(11 + a ), 1 ^ (2 + a ) x 2 + (1 - Л )(4 - a ) x 2 < Л (25 - a ) + (1 - Л )(23 + a ), где a , Л е [0,1].
Л ((4 - a ) x 1 + (3 - a ) x 2 + 1) + (1 - Л )((2 + a ) x 1 + (1 + a ) x 2 + 1) ^ max (13) p(1 + a ) x 1 + (1 - Л )(3 - a ) x 1 < Л (13 - a ) + (1 - Л )(11 + a ), [ Л (2 + a ) x 2 + (1 - Л )(4 - a ) x 2 < Л (25 - a ) + (1 - Л )(23 + a ), где a , Л е [0,1].
При Л = 1 задачи (12) и (13) сводятся к задачам (4) и (5) (рис. 7а). При Л = 0 задачи (12) и (13) сводятся к задачам к (6) и (7). На рис. 8 показано решение задачи (12)-(13) при Л = 1 (рис. 8а) и Л = 0,3 (рис. 8б). При a = 0 и Л = 1 разность значений целевой функции задач (12) и (13) равна 26 (рис. 7а), а при a = 0 и Л = 0,3 эта разность составляет всего 6 единиц (рис. 7б). Это показывает, что разработанный метод дает широкие возможности влиять на свойства задачи, на значения целевой функции, задавая величину Л .
Значение Л влияет и на функции принадлежности для множества допустимых решений Х задачи нечеткого линейного программирования, а также для удовлетворяющего (оптимального) решения X * задачи (3). На рис. 8а показано сравнение оптимальных значений задач (12)-(13) при a = 0; 0,1; 0,4; 0,6; 0,8; 1 при Л = 1, рис. 8б — Л = 0,3 (верхняя кривая — для задачи (12), нижняя — для (13)).
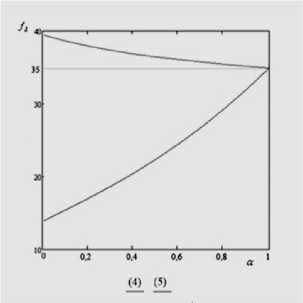
Рис. 8а. Сравнение значений задач (12)-(13) при Л = 1
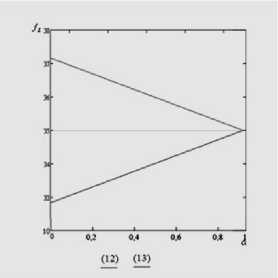
Рис. 8б. Сравнение значений задач (12)-(13) при X = 0,3
Так как при a = 0,9, X = 1 задача (12) имеет оптимальные значения x = 6,368, x2 = 8,31, то функция принадлежности имеет вид (8), а a = 0,9, X = 0,3 (xj = 5,863, x2 = 7,882), функция принадлежности имеет вид:
t — 5,863 17,589 — t ц, (x) = max {0, min{---------,----------}}, t e R, (14)
L 1 5,863 5,863
^ L 2
( x ) = max{0,min{
t — 15,768 31,528 — t 7,882 , 7,882
}}, t e R.
4. Обсуждение результатов
Сравнив функции принадлежности левой части первого ограничения задачи (12) при a = 0,9, X = 1 (рис. 9а) (совпадает с задачей (4)) и при a = 0,9, X = 0,3 (рис. 9б), можно увидеть, что во втором случае серединное значение левой части ближе к серединному значению правой части. На рис. 9а показан вид функций принадлежности левой и правой частей первого ограничения задачи (12) при a = 0,9, X = 1; рис. 9б — при a = 0,9, X = 0,3; (внешняя кривая — функция принадлежности левой части первого ограничения задачи (12), внутренняя — функция принадлежности правой части первого ограничения задачи (12)).
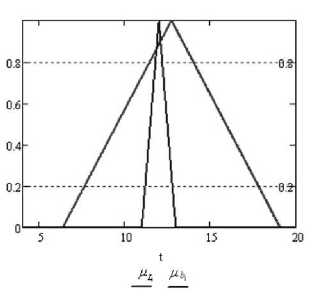
Рис. 9а. Функция принадлежности задачи (12) при a = 0,9, X = 1
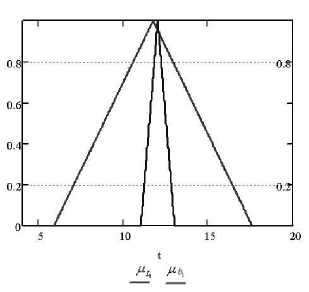
Рис. 9б. Функция принадлежности задачи (12) при a = 0,9, X = 0,3
Аналогичным образом можно сравнить функции принадлежности удовлетворяющего (оптимального) решения X * задачи (3) для случаев (12) и (13). На рис. 10а показан вид функций принадлежности ^ нечеткого отношения задачи (12) для первого ограничения при a = 0,9, X = 1; рис. 10б — при a = 0,9, X = 0,3.
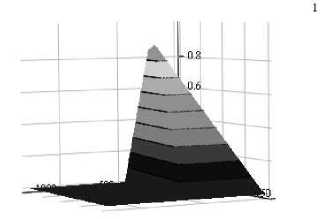
Рис. 10а. ц ~ задачи (12) при a = 0,9, X = 1
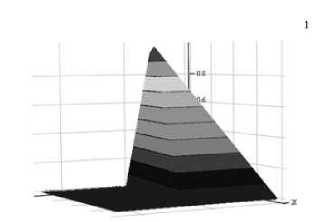
Рис. 10б. µ ≤ задачи (12) при a = 0,9, λ = 0,3
На рис. 10а sup µ ( L 1, b 1) ≈ 0,85 , а на рис. 8б sup µ ( L 1, b 1) ≈ 0,98 .
Приведенные результаты во втором случае, с точки зрения экспертного понимания природы этой задачи, свидетельствуют о большей степени «четкости» получаемых данных. Таким образом, при a = 0,9, λ = 0,3 степень нечеткости снижена и задача близка к четкой постановке.
5. Заключение
В данной статье рассмотрен известный [3] метод четырех задач нечеткого линейного программирования, который обобщен до параметрического a -уровневого метода λ -продолжения. Предложенный метод позволяет сократить количество рассмотренных случаев с четырех до двух, позволяет получать дополнительные решения на подмножествах квадрата a - λ . Преимущество такого подхода состоит в том, что он включает в себя четыре задачи как частные случаи. Новый подход позволяет получать более общие и гибкие решения, дает возможность влиять на свойства линейной задачи оптимизации: меру принадлежности, чувствительность, устойчивость. В статье также рассмотрен численный пример, показывающий работу нового метода и реализованный в программной среде MathCAD. Вышеизложенные исследования показывают, что нечеткий подход обобщает известную методику [1], но при этом усложняет расчеты. Полученные результаты нуждаются в интерпретации, которые возможны за счет анализа функций принадлежности и сферы применимости метода, экспертного понимания природы таких задач, например в экономической области, финансовых инвестиционных задачах.
Список литературы Параметрический α-уровневый метод λ-продолжения для задачи нечеткого линейного программирования
- Зайченко Ю. П. Исследование операций. Нечеткая оптимизация. Киев: Выща школа, 1991. 191 с.
- Беллман Р., Заде Л. Принятие решений в расплывчатых условиях//Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. С. 172-215.
- Задачи линейной оптимизации с неточными данными/М. Фидлер . М.; Ижевск: Изд-во ин-та компьютерных исследований, 2008. 288 с.
- Стародубцев И. Ю. Решение задачи линейного программирования с нечеткими параметрами//Технические науки -от теории к практике: материалы VI Междунар. науч.-практ. конф. Новосибирск: Изд-во СибАК, 2012.
- Пегат А. Нечеткое моделирование и управление: пер. с англ. 2-е изд. М.: БИНОМ, 2013.798 с.
- Шаталова А. Ю., Лебедев К. А. Нечеткое линейное программирование в задаче оптимального финансирования инвестиционных проектов, максимизирующей получаемый предприятием доход//Международный журнал прикладных и фундаментальных исследований. 2015. Ч. 1, № 9. С.35-36.
- Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими переменными. М.: Мир, 1975. 559 с.


