Переходы между электроконвективными режимами слабопроводящей жидкости при инжекции заряда в горизонтальных ячейках с разным аспектным отношением
Автор: Ильин В.А., Рушинская К.С.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 4 (39), 2017 года.
Бесплатный доступ
Изучены нелинейные режимы электроконвекции неизотермической слабопроводящей жидкости в постоянном электрическом поле горизонтального слоя при униполярной инжекции заряда с катода. Рассмотрены прямоугольные ячейки разной длины с условиями периодичности. Построены бифуркационные диаграммы режимов электроконвекции.
Электроконвекция, слабопроводящая жидкость, инжекция заряда
Короткий адрес: https://sciup.org/14730129
IDR: 14730129 | УДК: 532.5 | DOI: 10.1707211993-0550-2017-4-32-37
Текст научной статьи Переходы между электроконвективными режимами слабопроводящей жидкости при инжекции заряда в горизонтальных ячейках с разным аспектным отношением
Движение жидкостей в электрическом поле привлекает внимание тем, что представляет собой способ прямого преобразования энергии электрического поля в энергию движения жидкости [1, 2]. Знание законов действия электрического поля на конвективные течения актуально в связи с проблемой эффективного управления конвекцией, тепло- и массопереносом в различных технологических ситуациях, в частности, в электрогидро-динамических насосах.
Существует несколько механизмов электроконвекции в диэлектрических жидкостях: диэлектрофоретический механизм неустойчивости в идеальных диэлектриках [3], электрокондуктивный механизм неустойчивости в слабопроводящих жидкостях [4], инжекция заряда и диссоциационно-рекомбинационный механизм зарядообразования в слабопроводящих жидкостях [5].
В настоящей работе инжекционный механизм зарядообразования считается основным. Используется модель униполярной ин- жекции заряда, рассмотренная в [6–9]. Согласно этой модели плотность инжектируемого заряда с катода прямо пропорциональна напряженности электрического поля в слое жидкости.
В [6] рассмотрен изотермический случай, в [7] – подогрев сверху, в [8, 9] – подогрев снизу. Электроконвекция в длинных ячейках изучена в работе [10].
В настоящей работе исследуется электроконвекция в прямоугольных ячейках с разным аспектным отношением с условиями периодичности при разных нагревах снизу и в невесомости [11].
1. Постановка задачи
Рассмотрим бесконечный плоский горизонтальный слой вязкой несжимаемой сла-бопроводящей жидкости в вертикальном постоянном электрическом поле и поле тяжести с ускорением свободного падения g . Ось x направлена вдоль нижней границы слоя, ось z – перпендикулярна границам слоя.
Два плоских электрода лежат в плоскостях z = 0 и z = h (рис. 1), h - толщина слоя.
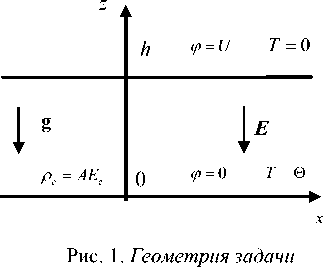
Идеально тепло- и электропроводные пластины конденсатора нагреты до разной температуры - T (0) = 0 , T ( h ) = 0. Здесь T -температура, отсчитываемая от температуры верхнего электрода, 0 - характерная разность температур. Случай 0 > 0 соответствует нагреву снизу.
На катоде (нижнем электроде) потенциал равен нулю р ( 0 ) = 0, на аноде (верхнем электроде) - р ( h ) = U . Здесь U - напряжение электрического поля.
С катода происходит униполярная инжекция заряда. Плотность свободных зарядов у катода пропорциональна нормальной составляющей вектора напряженности поля p e = aE z , где a - коэффициент, характеризующий степень инжекции.
Движение жидкости и свободных зарядов в слое описывается системой уравнений электрогидродинамики:
( dv p| — + (v ’V) v i дt
= -V p + pV o ^ V + p e E + p g ,
+ ( V -V ) T = xA T , д t
Р + div( p e v — b p e E ) = 0, (1)
дt divv = 0, p = p0(1 - 0T), div(££0E) = Pe, E = -Vp, где p - массовая плотность жидкости; v -вектор скорости жидкости; p - давление; v — коэффициент кинематической вязкости; pe -плотность заряда; х - коэффициент температуропроводности; в - коэффициент теплового расширения жидкости; £ - диэлектрическая проницаемость среды; £0 - электрическая постоянная; b – подвижность зарядов; E – напряженность, р - потенциал поля.
Границы слоя непроницаемые, на них выполняются условия прилипания – скорость равна нулю:
z = 0: v = 0, р = 0, p = - a —, T = 0, e дz z = h: v = 0, p = U, T = 0. (2)
Используем безразмерные переменные на основе масштабов: времени – время вязкой диссипации h 2 / v 0, расстояния - расстояние между электродами h , скорости - v 0 / h , потенциала – U , поля – U / h , давления – pV 2 / h 2, температуры - 0 , плотности заряда - ££ U / h .
После обезразмеривания система уравнений (1) с граничными условиями (2) приводится к виду
ГГ + (v-V)v = -Vp + Av - peV р + Ra Ty, дt M2 Pr cT ,
Pr — + (v-V) T = A T , дt divv = 0, Ap + pe = 0, (3)
p + (v-V)pe = -T2(pe2 -VP -Vpe) , дt M где y = (0, 0, 1), p - превышение давления над гидростатическим. Граничные условия имеют вид:
z = 0: v = 0, p = 0, p = -A—, T = 1, e дz z = 1: v = 0, p = 1, T = 0 . (4)
Здесь введены безразмерные параметры – тепловое число Рэлея Ra, электрические параметры Te и M, число Прандтля Pr, параметр инжекции A:
V 0 X b pv 0
Pr=v«, A=ah.(5)
X££
Рассматриваются плоские возмущения v = ( u ,0, w ) и д/д y = 0 , вводится функция тока ψ и вихрь скорости Φ:
д^д
Vx =--, vz =---, Ф = (rot v ), =-A ^ .
xzy
В рамках безындукционного приближения безразмерная система уравнений электроконвекции слабопроводящей жидкости имеет вид:
дФ д w дФ д w дФ . _
— + —----—--= АФ - д t дx дz дz г Te2 ^ _ Ra дРе
E,
M2 дx Pr дРе дЩ дРе дЩ дРе T2 ( 2 , дРРе >
д t д x д z д z д x Pr
Граничные условия следующие:
z = 0: w = 0, — = 0, Р = AE, T = 1, дz e z = 1: w = 0, — = 0, T = 0. дz
На боковых границах для всех искомых функций выполняются условия периодичности.
2. Результаты
Задача решалась методом конечных разностей [12]. Эволюционные уравнения решались по явной схеме, конвективные слагаемые в уравнении для заряда и температуры аппроксимировалась разностями "против потока". Для уравнения переноса тепла использовались центральные разности. Для удобства работы с условиями периодичности к сетке добавлялись два вертикальных ряда. Вихрь скорости на горизонтальных границах вычислялся по формуле Тома. Для решения уравнения Пуассона использовался метод последовательной верхней релаксации.
Число Прандтля Pr = 10, электрический параметр M = 14,14. Расчеты проведены при разных значениях параметра T e и теплового числа Рэлея Ra. Для вычислений выбиралась прямоугольная ячейка с пространственными размерами L z = 1, L x = 4; L z = 1, L x = 10. Число узлов по вертикальной и горизонтальной осям бралось соответственно 21×81; 21×201.
Результаты расчетов систематизированы. Обнаружены два режима стационарной конвекции, между которыми наблюдались гистерезисные переходы [9]. Предварительные результаты для разных ячеек опубликованы в работе [11]. На рис. 2 представлены результа- ты расчетов зависимости максимального значения функции тока щт от электрического параметра Te для Ra = 1000 и сетки 21×201 узлов.
Нижний режим 1 имеет меньшую интенсивность движения вихрей, верхний режим 2 – большую интенсивность. Существует конкуренция между режимом 2 и равновесием, режимами 1 и 2 в соответствующих интервалах управляющего параметра.
Результаты расчетов для ячейки L z = 1, L x = 2 представлены в работе [9]. Пороги переходов между режимами электроконвекции, полученные при вычислении зависимости максимального значения функции тока от параметра T e для Ra = 1000 и для L x = 4, 10 представлены в таблице.
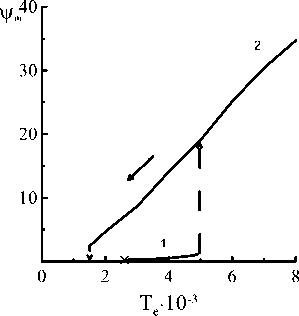
Рис. 2. Зависимость максимальной функции тока от T e для Ra = 1000 (L z = 1, L x = 10)
Для ячейки L z = 1, L x = 2 нижний режим начинается при T e = 2,5 - 10 3 ; для L z = 1, L x = 4 -при T e = 2,8 - 10 3 ; для L z =1, L x = 10 - при T e = 2,6 - 10 3 .
Для ячейки L z = 1, L x = 2 с ростом поля при T e = 5,5 - 10 3 происходит скачкообразный переход к режиму конвекции 2 с большей интенсивностью вихрей; для L z = 1, L x = 4 – при T e = 4,9 - 10 3 ; для L z = 1, L x = 10 - при T e = 5 - 10 3 .
Для ячейки Lz = 1, Lx = 2 в интервале 1,6 -103 < Te < 5,5 -103 обнаружен гистерезис, в котором поведение системы существенно зависит от начальных условий. При вычислении методом продолжения по параметру выявлено, что при движении в пространстве параметров справа налево режим 2 существует до Te =1,6 -103. При меньшей напряженности поля в системе независимо от начальных условий затухают все возмущения, и устанавливается равновесное распределение переменных. При больших размерах ячейки эти интервалы переходов следующие: 1,4⋅103 ≤ Te ≤ 4,9⋅103 для Lz = 1, Lx = 4; 1,5⋅103 ≤ Te ≤5⋅103 для Lz = 1, Lx = 10.
Для ячейки L z = 1, L x = 2 в интервале 1,6 ⋅ 103 ≤ T ≤ 2,4 ⋅ 10 3 в зависимости от начальных условий в системе будет либо равновесие, либо стационарный режим 2, при большем поле: 2,5 ⋅ 103 ≤ T ≤ 5.4 ⋅ 103, реализуется либо режим 1, либо режим 2. При T > 5.4 ⋅ 103 сколь угодно малые возмущения равновесия приводят систему после переходных процессов к стационарному режиму 2.
Пороги возникновения нелинейных режимов и переходов от одного режима к другому при Ra = 1000 для различных размеров ячейки
|
Ra |
L x |
Порог возникновения верхнего режима (2), T e , 103 |
Порог возникновения нижнего режима (1), T e , 103 |
Порог перехода от нижнего режима (1) к верхнему (2), Te , 103 |
|
1000 |
2 |
1,6 |
2,5 |
5,5 |
|
1000 |
4 |
1,4 |
2,8 |
4,9 |
|
1000 |
10 |
1,5 |
2,6 |
5,0 |
|
500 |
2 |
1,5 |
4,4 |
5,7 |
|
500 |
4 |
1,5 |
4,1 |
5,1 |
|
500 |
10 |
1,5 |
4,0 |
5,1 |
|
0 |
2 |
1,5 |
- |
6,3 |
|
0 |
4 |
1,5 |
- |
5,4 |
|
0 |
10 |
1,5 |
- |
5,4 |
Обнаружено, что, когда число Рэлея становится меньше, порог режима 2 практически не изменяется, при этом пороги переходов между режимами растут, и ширина существования режима 1 уменьшается.
В состоянии невесомости (Ra = 0) режим с малой интенсивностью вихрей исчезает, и остается только режим с большой интенсивностью вихрей. Увеличение размеров ячейки приводит к изменению порогов перехода между режимами.
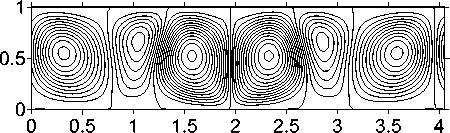
На рис. 3 приведены изолинии функции тока для режима 1 (T e = 4,5 ⋅ 103) (а) и режима 2 (T e = 7 ⋅ 103) (в) при Ra = 500, L x = 4. В такой ячейке существует 6 вихрей. Вихри в режиме 1 симметричные, а в режиме 2 – несимметричные.
На рис. 3 также приведены изолинии температуры – для режима 1 (б) и для режима 2 (г). Во втором режиме вихревое движение и тепло-перенос более интенсивные, чем в первом.
Для других ячеек интервалы меняются.
Для L z = 1, L x = 4 они таковы: 1.4 ⋅ 103 ≤ T ≤ 2.7 ⋅ 103; 2.8 ⋅ 103 ≤ T ≤ 4.8 ⋅ 103.
Переход на верхний режим происходит при T > 4.8 ⋅ 103.
Для L z = 1, L x = 10 первый интервал гистерезиса следующий: 1.5 ⋅ 103 ≤ T ≤ 2.5 ⋅ 103, второй – 2.6 ⋅ 103 ≤ T ≤ 4.9 ⋅ 103.
( в )
Переход на верхний режим совершается при T > 4.9 ⋅ 103 .
Также были проведены расчеты для других нагревов снизу, меньших числах Рэлея. В таблице представлены пороги переходов между режимами.
( г )
Рис. 3. Изолинии функции тока (а) и температуры (б) при Ra = 500, L x = 4 для режима 1 (T e = 4,5 ⋅ 103); и изолинии функции тока (в) и температуры (г) для режима 2 (T e = 7 ⋅ 103)

0 1 2 3 4 5 6 7 8 9 10

0 1 2 3 4 5 6 7 8 9 10

( в )

0 1 2 3 4 5 6 7 8 9 10
( г )
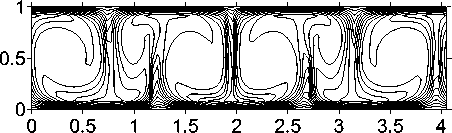
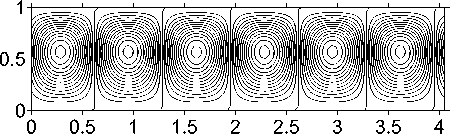
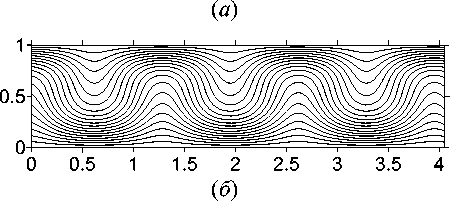
Рис. 4. Изолинии функции тока (а) и температуры (б) при Ra = 500, L x = 10 для режима 1 (T e = 4 ⋅ 103); и изолинии функции тока (в) и температуры (г) для режима 2 (T e = 7 ⋅ 103)
На рис. 4 приведены изолинии функции тока для режима 1 (T e = 4 ⋅ 103) (а) и режима 2 (T e = 7 ⋅ 103) (в) при Ra = 500, L x = 10. В такой ячейке у нижнего режима наблюдается 14 вихрей, а у верхнего – 10 вихрей.
На рис. 4 также приведены изолинии температуры – для режима 1 (б) и для режима 2 (г). Отметим, что во втором режиме вихревое движение и теплоперенос более интенсивны, чем в первом.
Заключение
В работе изучена динамика нелинейных режимов электроконвекции неизотермической слабопроводящей жидкости при униполярной инжекции заряда в постоянном электрическом поле горизонтального конденсатора. Исследована конвекция в прямоугольных ячейках для разных соотношений сторон конвективной ячейки с условиями периодичности при разных нагревах.
Система имеет два различных по интенсивности нелинейных стационарных режима конвекции. Построены бифуркационные диа- граммы. Проанализированы и изучены соответствующие пороги и гистерезисные переходы между различными типами движений.
Список литературы Переходы между электроконвективными режимами слабопроводящей жидкости при инжекции заряда в горизонтальных ячейках с разным аспектным отношением
- Остроумов Г.А. Взаимодействие электрических и гидродинамических полей: Физические основы электрогидродинамики. М.: Наука, 1979. 320 с.
- Саранин В.А. Устойчивость равновесия, зарядка, конвекция и взаимодействие жидких масс в электрических полях. М.; Ижевск: НИЦ РХД, 2009. 332 с.
- Ильин В.А. Маломодовая модель электроконвекции идеального диэлектрика//Журнал технической физики. 2010. Т. 80, вып. 8. С. 38-48.
- Ильин В.А. Электроконвекция слабопроводящей жидкости в постоянном электрическом поле//Журнал технической физики. 2013. Т. 83, вып. 1. С. 64-73.
- Стишков Ю.К., Чирков В.А. Неравновесные механизмы электризации слабых электролитов при воздействии постоянного напряжения//Журнал технической физики. 2016. Т. 86. Вып. 7. С. 1-8.
- Верещага А.Н. Унарная электроконвекция в плоском слое//Гидродинамика и процессы тепломассопереноса. Свердловск: Уральское отделение академии наук СССР, 1989. С. 42-47.
- Мордвинов А.Н., Смородин Б.Л. Электроконвекция при инжекции с катода и нагреве сверху//Журнал экспериментальной и теоретической физики. 2012. Т. 141, вып. 5. С. 997-1005.
- Ильин В.А., Мордвинов А.Н., Петров Д.А. Электроконвекция слабопроводящей жидкости при униполярной инжекции заряда в постоянном электрическом поле//Журнал экспериментальной и теоретической физики. 2015. Т. 147, вып. 1. С. 181-188.
- Ильин В.А. Электроконвекция слабопроводящей жидкости в горизонтальном конденсаторе при униполярной инжекции заряда//Журнал технической физики. 2017. Т. 87. Вып. 1. С. 5-9.
- Smorodin B.L., Taraut A.V. Simulations of oscillatory electroconvection in a horizontal capacitor with a large aspect ratio//Magnetohydrodynamics. 2016. Т. 52, № 1. С. 245-254.
- Рушинская К.С., Ильин В.А. Электроконвекция слабопроводящей жидкости при инжекции заряда в горизонтальных ячейках с разным аспектным отношением//Материалы международного симпозиума "Неравновесные процессы в сплошных средах". Пермь, 2017. Т. 2. С. 172-174.
- Тарунин Е.Л. Вычислительный эксперимент в задачах свободной конвекции. Иркутск: Изд-во Иркут. ун-та, 1990. С. 228.


