Планирование траекторий промышленных роботов на основе нейронных сетей

Эффективное внедрение роботизированных технологических комплексов (РТК) тесно связано с созданием систем автономного программирования роботов. При этом одной из наиболее трудоемких задач является планирование траектории манипулятора в рабочей среде с препятствиями. Эта задача заключается в нахождении последовательности локаций робота, движение по которым не приводит к столкновениям с препятствиями, причем начальная и целевая конфигурации заданы заранее.

Большинство современных методов планирования траектории промышленных роботов основаны на модели конфигурационного

пространства манипулятора, заданной в виде дискретного множества свободных от столкновений конфигураций. Это множество формируется на основе вероятностных алгоритмов [1-3] либо детерминистических [4-5].

В данной статье предложен новый метод планирования траекторий роботов-манипуляторов в рабочей среде с препятствиями, основанный на детерминистической дискретизации конфигурационного пространства. В отличие от известных этот метод учитывает сложную форму препятствий, характерную для сборочно-сварочных роботизированных комплексов. Предложенный подход основан на топологически упорядоченной нейронной сети, которая моделирует весовую функцию,

ИССЛЕДОВАНИЯ

HAVKO____________ Ж ГРАДА

характеризующую расположение робота-манипулятора относительно препятствий.

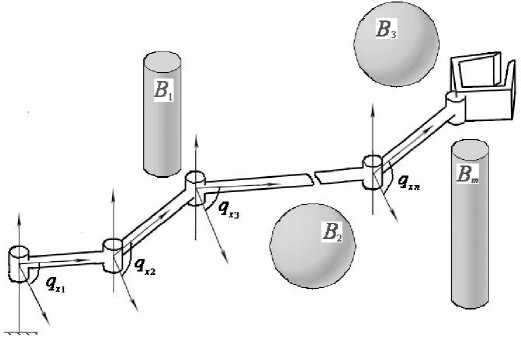
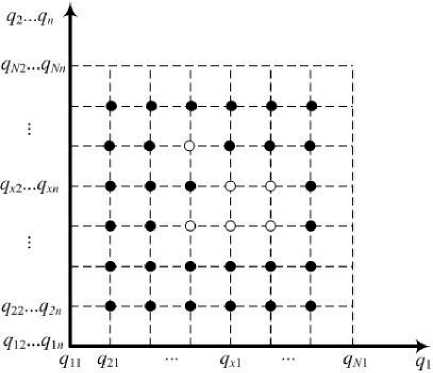
Рассмотрим робот-манипулятор с n поворотными сочленениями (рис. 1, а ), в рабочей зоне которого расположено некоторое множество препятствий B = { B 1 , B ₂, „., B m }. Если конфигурационное пространство этого робота дискретизировано с разрешением N , то угол в каждом из сочленений j (j' = 1: n ) может принимать дискретные значения q j ( xj e {1, ..., N }), при этом величины q _{1 j} и q_Nj задают нижнее и ³⁸ верхнее конструктивные ограничения на углы в сочленениях (рис. 1, б ). Тогда дискретная модель конфигурационного пространства рассматриваемого робота может быть представлена в виде множества из Nⁿ векторов

DC ={ q a_l\ a = 1... N n }            ⁽¹⁾

где q = [ q ] T - дискретная конфигурация робота ( xj e {1, ..., N }), a - одномерный индекс, значения которого вычисляются по формуле a = N n ^{- 1} x 1 + Nⁿ - ² x 2 + ... + xn - 3 .

Множество свободных от столкновений конфигураций робота-манипулятора определяется следующим образом:

DC. f = { q , e DC\M ( q , ) n B = 0 } , (2)

где М ( q , ) - робот-манипулятор М , установленный в конфигурацию q _a .

Прямолинейный участок траектории между двумя конфигурациями q, и qb (a * b, q,, qb eDC,) задается в виде множества векторов d .b = {d«M (dk )^ B = 0}, (3)

где d k = q . + ( h / Nh )( q b - q , ), h = 0: Nh , Nh >  N - параметр дискретизации прямолинейного участка траектории.

Дискретная конфигурация робота q b e DC является соседней с конфигурацией q , e DC f , если между ними существует прямолинейный участок траектории d _,b и индекс b удовлетворяет одному из соотношений

Ь 1 = , - N^{n 1} ^ ( х 1 - 1, x 2, . , xn ) , b ₂ = = , + N n ^{- 1} ^ ( x 1 + 1, x 2,. . , xn ) ,

b_d - 1 = , - 1 ^ ( x 1, x 2, ... , xn - 1 ) , b_d = = , + 1 ^ ( x 1, x 2, . , xn + 1 ) .

№ 1 (1) январь-март 2012

Таким образом, каждая конфигурация q , может иметь d <  2 n соседних конфигураций.

Траектория, соединяющая стартовую qs 1 и целевую qs конфигурации робота, представляет собой последовательность, состоящую из соседних конфигураций qs 1, qs2,., qsg eDCf и прямолинейных участков, соединяющих эти конфигурации ds 1 s2, ds 1 s2, . d(sg—1)sg. Критерий «качества» траектории в дискретном конфигу- рационном пространстве зададим в виде g-1

J = ^ T sk ( sk + 1 ) ( d sk ( sk + 1 ) )’ k = 1

где T_{sk ( sk+ 1)} - значение весовой функции для прямолинейного отрезка траектории d _{sk ( sk+ 1)}.

Тогда задача планирования траектории в дискретном конфигурационном пространстве может быть сформулирована следующим образом: среди всех последовательностей дискретных конфигураций qs 1, qs2, .„, qsgeDCf, координаты которых лежат внутри области, ограниченной предельно допустимы ми значениями углов в сочленениях q 1j и qNj (j' = 1:n), найти последовательность, на которой достигает минимума критерий (5).

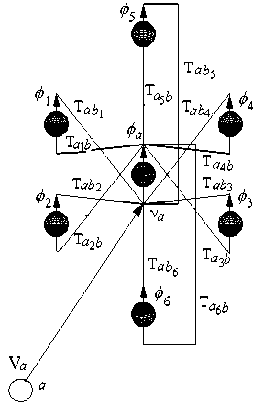
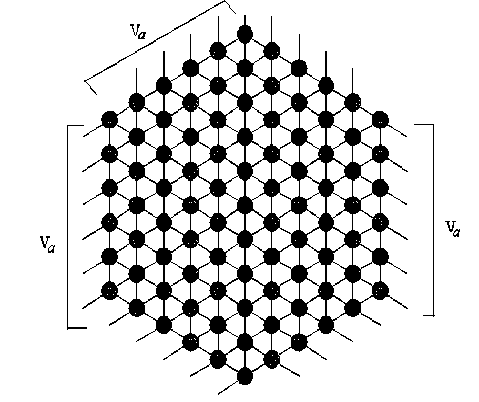
Для решения сформулированной выше задачи планирования траектории предлагается использовать метод, основанный на топологически упорядоченной нейронной сети. Предложенная модификация нейронной сети представляет собой множество, состоящее из Nⁿ нейронов, которые распределены над областью n -мерного конфигурационного пространства. Таким образом, каждой дискретной конфигурации робота q _, ставится в соответствие нейрон с индексом , , соединенный с d соседними нейронами, имеющими индексы b k , k = 1. d . Значения индексов b k определяются в соответствии с (4), таким образом, расположение нейрона в системе координат нейронной сети соответствует некоторой конфигурации робота. Каждому прямолинейному участку траектории между двумя соседними конфигурациями q _, и q _b ставилась в соответствие величина весовой связи между нейронами а и b , равная T_abk . Пример такой структуры для робота с тремя степенями свободы ( n = 3) представлен на рис. 2. Здесь на вход нейрона а поступает 6 взвешенных сигналов от соседних нейронов ^T ,b 1 Ф 1 , ^T ,b 1 Ф 2 ^, .^, Ta b 6 Ф б (рис. 2, а ), где T_{ab 1} - T_{ab 6} – весовые коэффи2иенты.

Также на вход каждого нейрона а поступает внешний сигнал V_a (рис. 2, б ), значение которого определяется следующим образом:

а

Планирование траекторий промышленных роботов на основе нейронных сетей

б

Рис. 1. Робот-манипулятор и его дискретное конфигурационное пространство

V a = -1, если q a t DC, либо q a = [ q 1 j ]^T = 1: n ), либо q a = ^[ q ^T < j• = 1: n ); V = 1, если q a = q_s g ; V = 0

во всех остальных случаях.

Распределение потенциалов ф а ( a = 1: Nⁿ ) на выходе нейронной сети с такой структурой определяет потенциальное поле робота-манипулятора в соответствии со следующей системой уравнений:

dv„ Nn_ фa = fa (Va ), Ta ~± = ZTabФb — Ta0Va + Va , (6) d t    b=1

где f(va) - функция активации нейрона а; va - значение потенциала на входе нейрона а; фb- значение потенциала на входе нейрона b, соседнего с нейроном а; тa, Tab, Ta0 - весовые коэффициенты нейронной сети.

Значения потенциалов, соответствующие для каждой конфигурации q a , вычисляются путем численного решения (6) на основе следующей итерационной формулы:

( dА

Ф('+1)= f, Z Tab к ф(') + Va •<7>

V к =1

где l - номер итерации.

Введем следующие обозначения: N ₀ -начальное значение параметра дискретизации конфигурационного пространства; N _max - максимально допустимое значение пара-

а

б

Рис. 2. Топологически упорядоченная нейронная сеть

■J ИССЛЕДОВАНИЯ

Havko-

ЖГРАДА

№ 1 (1) январь-март 2012

метра дискретизации конфигурационного пространства; Ns – шаг изменения параметра дискретизации; P - траектория робота. В предложенном алгоритме используются следующие функции: maxf( фb ) - функция, возвращающая максимальное значение потенциала ф из множества фbk; maxb(фb ) - функция, возвращающая индекс b максимального ектории между двумя конфигурациями робота q(φa) и q(φb) в соответствии с формулой (3). Если такой участок траектории существует, данная функция возвращает значение «1», в противном случае она возвращает значение «0».

Предложенный алгоритм планирования траектории имеет следующий вид:

Исходные данные: геометрическая модель робота и препятствий, стартовая q s 1 и целевая q s конфигурации

1:  Установить начальное значение параметра дискретизации N←N ₀;

2: повторять

3:       Вычислить V_a для параметра дискретизации N ;

4:       Установить весовые коэффициенты нейронной сети в T_abk ← 1/3 n ( k =1: d );

• 5:        повторять

• 6:            Вычислить потенциальное поле φ _a ( a =1: Nⁿ ) используя (7);

• 7:              a H s 1;

• 8:             повторять

• 9:

^фн maxf( ^ф b k );

• 10:

b H maxb (ф _b );

• ^11:                    p ^н explore ⁽ q ^{( ф} a ), q ^{( ф} b ));

• 12:                  p H q ( ф a ), q ( ф b )};

• 13:               если b = sg то возвратить траекторию P ;

14:                 a H b ;

15:            до тех пор пока p =0;

16:

17:

18:

19:

20:

T abk ← 0;

P ← 0;

до тех пор пока ф s 1 =0;

N H N + N ;

s до тех пор пока N

Время генерации траектории при различных значениях параметра дискретизации

Таблица 1

Параметр дискретизации N	Количество тестов столкновения	Время генерации вектора Va, с	Время генерации потенциального распределения, с	Время градиентного поиска, с
20	8000	0,15	0,3	0,02
50	25000	4,1	22,3	0,11
100	1000000	12,2	122,2	0,23

значения потенциала из множества φ_bk; q(φ) - функция, возвращающая конфигурацию робота, соответствующую значению потенциала φ; explore(q(φ_a), q(φ_b)) - функция проверки существования прямолинейного участка тра-

Исследование эффективности предложенного метода выполнялось в среде САПР ROBOMAX. В качестве объекта использовалась роботизированная ячейка, включающая робот-манипулятор KR125, оснащенный

Планирование траекторий промышленных роботов на основе нейронных сетей сварочными клещами, свариваемую деталь (деталь кабины автомобиля ГАЗель), кондукторную плиту и технологическую оснастку. В качестве препятствий в данном случае рассматриваются сварная конструкция, технологическая оснастка, а также кондукторная плита. Для различных значений параметра дискретизации N экспериментально было определено количество тестов столкновений и приблизительное время вычислений (табл. 1). Из таблицы видно, что алгоритм сходится за приемлемое для практики время: 0,47 с, 26,51 с, 134,6 с при дискретности конфигурационного пространства 8000, 25 000 и 1 000 000 узлов соответственно.