Подготовка студентов юридических направлений в современных условиях

Технический прогресс и политика государства в области цифровизации экономики требует модернизации имеющейся в России правовой нормативной базы и создания новой по аналогу уже существующей в мировой практике с адаптацией под местные условия с учетом традиций. В своем выступлении глава «Сбербанка» Герман Греф заявил, что в современном обществе цифровизация играет решающую роль и юристам необходимо либо освоить новые технологии, понять, как работают нейронные сети и искусственный интеллект, либо распрощаться с профессией. Существует экспертное мнение о том, что процесс цифровизации права и законотворчества это процесс алгоритмический с четким набором указаний для его исполнения. Поэтому особое внимание в современных условиях следует уделять подготовке юристов новой формации. Студентов нужно научить «мыслить юридическими категориями», при этом «роль математического образования в процессе подготовки специалистов любого профиля на каждом из исторических этапов зависит от принятой образовательной парадигмы государства, от структуры высшего образования, от степени развития самой науки и от развития научных областей знаний в целом» [1, с. 101]. Для достижения постав- ленных образовательных целей и задач целесообразно обязательное включение в учебные планы дисциплины математика, наряду с такими дисциплинами, как: экономика, информатика, информационные технологии в профессиональной деятельности, основы информационной безопасности.

Юриспруденция относится к гуманитарным направлениям подготовки, поэтому зачастую бытует мнение о том, что юристам не требуется математическая подготовка. Исключение из учебных планов подготовки юристов дисциплины «математика» приводит к тому, что студенты не изучают «азбуку» мышления и теоретические основы анализа. Элементарные навыки построения предложений по определению понятий в юриспруденции, так же, как и в математике требуют знаний определенного свода правил (законов). Как говорил М.В. Ломоносов «Математику уже затем учить надо, что она ум в порядок приводит».

Современный юрист должен обладать не только острым умом и способностью к мышлению, но и навыками анализа ситуации, выделения главного и второстепенного, определения понятий и категорий и установления соответствий между фактами, причинами и следствием. Он должен четко уметь выделять причину и следствие, находить соответствующие обоснования в законодательной базе. Но изучение математики юристами не должно сводиться к изучению только отдельных ее разделов, например, теории вероятностей и не должно сводиться к изучению математики для экономистов, либо математики для технических специальностей.

Математика для юристов должна включать разделы, которые позволят изучить основные методы и приемы абстрагирования, сформировать умения моделировать процессы и ситуации, развить навыки построения правильной речи при определении понятий. Подготовка студентов юридических направлений должна быть нацелена на формирование умения строить свою речь по правилам определения математических понятий через родовое понятие и видовое отличие.

Рассмотрим пример: студентам на одной из первых лекций по математике предлагается дать определение окружности используя знания средней школы. Распространенный ответ студентов: «окружность это которая ….., ну, вокруг некоторой точки». Далее следует уточняющий диалог:

Преподаватель: – окружность, это «которая»?

Студенты: – нет! Это фигура!

Преподаватель: – конкретизируйте, то такое «фигура»?

Студенты: – это линия!

Преподаватель: – какая линия (рисует да доске прямую линию), такая?

Студенты: – нет кривая!

Преподаватель: – конкретизируйте (рисует на доске кривую линию), такая?

Студенты: – нет, должна быть точка «центр»!

Преподаватель: – что такое линия?

Студенты: – это множество точек….

Преподаватель: – любых?

Студенты: – нет, которые находятся на одинаковом расстоянии от центра.

Преподаватель подводит итог: окружность это (что?) множество точек, (каких?) равноудаленных от некоторой точки О, называемой центром.

Данный пример наглядно иллюстрирует отсутствие у студентов знаний в области формального построения определения понятий, в данном случае математических. Для успешного освоения дисциплин учебного плана и установления взаимопонимания между студентами и преподавателями необходимо научить студентов правилу определения понятий: сначала всегда определяем «что это», т.е. даем «родовое понятие», а затем уточняем, чем это понятие отличается от других, чтобы конкретизировать определение, отвечаем на вопрос «какое», т.е. указываем отличительный признак – видовое отличие. В дальнейшем при изучении курса математики у студентов необходимо выработать устойчивый навык правильно строить свою речь при определении любых понятий. Работа студентов с «категорийным» математическим аппаратом на первом курсе позволяет сформировать базовые умения и навыки правильного построения предложений в ходе рассуждений при определении любых понятий, не только математических. Такая методика позволяет улучшить успеваемость студентов по дисциплине математика, формировать интерес к изучению дисциплины «математика», ликвидировать ложное представление о неспособности изучения математики гуманитариями, сформированное в школе. Это является одним из важных фактором создания условий успешности в профессиональном образовании и в будущей деятельности юриста.

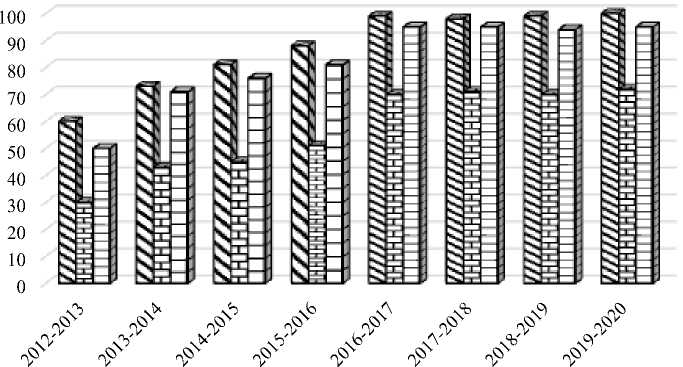
Данная методика применялась в ЮжноУральском государственном университете (ЮУрГУ) при обучении студентов 1 курса очной формы обучения по специальности 40.05.02 Правоохранительная деятельность с 2012/2013 учебного года. Все виды занятий по математике со студентами юридического направления подготовки проводились в сотрудничестве, с обязательным вовлечением даже в теоретическое лекционное занятие большого количества студентов. На практических занятиях использовались разноуровневые задания [2] и обязательное деление группы на микрогруппы [3], которые формировались по собственному желанию студентов, с обязательным распределением их по зонам в пространстве большой аудитории. В микрогруппе [4] работали студенты: разного уровня знаний математики (по симпатиям – более сильные студенты оказывали консультативную помощь более слабым в математике студентам); одинаково высокого уровня знаний математики (студенты работали на соревновательной основе, обычно отсаживались в конец аудитории, т.к. обычно вели себя довольно шумно); среднего уровня подготовленности (в основном работали самостоятельно, с невысоким темпом работы при консультации преподавателя или назначенного им консультанта из числа более сильных сту- дентов); низкого уровня подготовки (рассаживались на первых партах перед преподавателем и работали с наглядным разбором заданий на доске под непосредственным руководством преподавателя). При этом студенты могли свободно перемещаться по аудитории, переходить из группы в группу, при условии соблюдения рабочей обстановки в аудитории и относительной тишины. В представленной ниже диаграмме приведен анализ качественной успеваемости студентов 1 курса очной формы обучения по специальности 40.05.02 Правоохранительная деятельность (рис. 1).

и Критерии оценки □ Критерии оценки □ Критерии оценки

Рис. 1. Показатели качества

При изучении дисциплины «Математика» в результате использования данной методики параллельно с применением элементов балльно-рейтинговой системы обучения (2013/2014 – 2018/2019) и в дальнейшем – внедрением балльнорейтинговой системы обучения (с 2019/2020) для студентов 1 курса очной формы обучения по специальности 40.05.02 Правоохранительная деятельность снизился процент пропуска занятий по неуважительной причине с 50% до 5% и устойчиво держится на одном уровне. Количество студентов, получивших оценки неудовлетворительно по промежуточной аттестации снизилось до 5%.

Таким образом, можно сделать вывод, что применение описанной методики обучения студентов юридических направлений позволяет сформировать у студентов интерес к обучению, повысить успеваемость по дисциплине «Математика», снизить «боязнь» выступления перед аудиторией (развитию которой способствует система повсеместного тестирования), а как известно, профессия юриста – профессия публичная. Дальнейшие исследования в данном направлении планируется расширить на изучение и анализ работы выпускников данной специальности после их трудоустройства.