Подход к твёрдотельному моделированию геометрических объектов в точечном исчислении

Процесс современного проектирования невозможно представить без использования систем автоматизированного проектирования (САПР), которые стали эффективным инструментом геометрического моделирования. Геометрические модели прошли многоэтапный процесс эволюции, начиная от ручного черчения, двухмерного и трёхмерного моделирования, использования облачных технологий и цифровой поддержки жизненного цикла изделий до использования средств искусственного интеллекта и машинного обучения.

Существующие САПР хорошо подходят для решения инженерных задач с ограниченным количеством объектов, но пока не могут обеспечить достаточную производительность для создания полноценных цифровых двойников, включающих большие массивы трёхмерных элементов. Другим недостатком современных САПР является отсутствие программного обеспечения, объединяющего возможности геометрического моделирования (CAD) и расчётных САПР (CAE), что приводит к необходимости импорта геометрических моделей объектов в расчётные комплексы и к возникновению проблем, связанных с недостаточной интероперабельностью отечественных и зарубежных САПР. Основой современных САПР является геометрическое ядро и математический аппарат, на основе которого оно реализовано.

1    Теоретическая часть

Существует несколько видов представления геометрических моделей в САПР, которые включают точечную, каркасную, граничную, конструктивную и воксельную 1 модели. Наибольшее распространение в САПР имеет граничная модель [1], которая получила аббревиатуру BREP ( Boundary REPresentation ) или B - rep [2-4]. Стоит отметить, что геометрически не совсем корректно называть замкнутую оболочку полноценной твёрдотельной моделью (ТМ), но эта условность используется, в т.ч. и в формате представления данных IFC 2 .

Среди отечественных разработчиков геометрического ядра САПР можно выделить два программных продукта: C3D [5, 6] и RGK [7, 8]. Оба этих геометрических ядра используют граничную модель BREP . В работах [9, 10] показано, что поверхность (оболочка) – это двухпараметрическое множество точек, а геометрическое тело – это трёхпараметрическое множество, принадлежащее трёхмерному пространству. В обоих случаях речь идёт о переменных или текущих параметрах, а под геометрическим телом понимается геометрическое множество точек, у которого количество текущих параметров соответствует размерности пространства [9]. Одномерным геометрическим телом является отрезок прямой – выделенная часть одномерного пространства, двумерным телом – выделенная часть плоскости и т.д., а нульмерным геометрическим телом является точка – уникальный геометрический объект, который не имеет никаких метрических характеристик и вместе с тем любой геометрический объект можно представить организованным множеством точек.

Для аналитического описания кривых, поверхностей и гиперповерхностей многомерного пространства разработан математический аппарат «Точечное исчисление» [11]. Точечное исчисление используется также для моделирования геометрических тел, как выделенной части пространства, заполненного организованным множеством точек [9, 10]. Похожий подход, основанный на методах многомерной интерполяции, предложен в [12-14] и реализован на другом математическом аппарате.

Близкой к описанию геометрических тел является воксельная модель, обеспечивающая представление объектов в виде трёхмерного массива объёмных элементов [15-17]. Воксель-ная модель является обобщением растровой модели на трёхмерное пространство и унаследовала все недостатки растровых моделей, к которым относятся: большие массивы информации, необходимые для представления объёмных данных; значительные затраты оперативной памяти; трудности, связанные с увеличением или уменьшением изображений. Моделирование геометрических тел в виде организованного множества точек можно представить как векторное представление воксельных моделей. Если размер вокселя устремить к точке, то геометрические объекты можно описать организованным множеством точек, получив векторные модели, которые более предпочтительны в САПР по сравнению с растровыми.

ТМ, схожая с воксельной, используется в CAE , реализованных на основе метода конечных элементов (МКЭ) [18,19]. При стремлении размера объёмного элемента к бесконечно малой величине (точке) получается точечная ТМ, близкая к предложенной, но вычислительная сложность МКЭ при этом стремится к бесконечности. Если использовать представление

1 Воксел (от англ. volumetric pixel или voxel — объёмный пиксель) — элемент объёмного изображения, содержащий значение элемента растра в трёхмерном пространстве.

• ²    IfcGeometricConstraintResource.

геометрических объектов с помощью текущей точки, которая своим движением заполняет пространство, то можно получить модель, которая описывается простыми точечными уравнениями. Эти уравнения сводятся к системе однотипных параметрических уравнений, позво- ляющих реализовать параллельные вычисления по данным на уровне математического аппа- рата [20].

Пример моделирования геометрического тела предложенным способом (см. рисунок 1).

Для параметризации ТМ параллелепипеда можно воспользоваться простыми отношениями трёх точек прямых DA , DB и DC на его сторонах:

DP   DQDR и =    , v =----, w =

DA   DBDC

В результате получаются три точечных уравнения прямых:

P = ( A - D ) и + D , Q = ( B - D ) v + D , R = ( C - D ) w + D.

Для определения текущей точки М трёхпараметрического множества можно дважды воспользоваться точечной формулой параллельного переноса [11]:

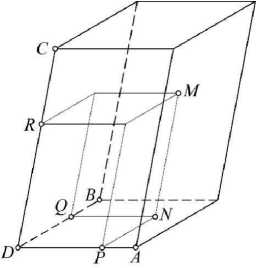
Рисунок 1 - Геометрическая схема определения твёрдотельной модели параллелепипеда

N = P + Q - D

M = R + N - D

^ M = ( A - D ) и + ( B - D ) v + ( C - D ) w + D .

В уравнении (1) A, B , C , D - исходные точки, которые не только формируют локальный симплекс трёхмерного пространства для определения искомого множества точек, но и однозначно определяют положение и размеры параллелепипеда в глобальной системе координат. Параметры и , v , w в предложенной параметризации (рисунок 1) изменяются от 0 до 1, обеспечивая заполнение точками внутренней части параллелепипеда. Используя свойства точечного исчисления, можно представить уравнение (1) в более компактном виде:

M = Au + Bv + Cw + D ( 1 - и - v - w ) .

Эти две формы представления геометрических объектов в точечном исчислении являются полностью идентичными и всегда могут быть получены одна из другой. Выбор формы представления точечного уравнения зависит от конкретной задачи и определяется удобством использования. Под точками A, B, C, D, M в уравнении (1) понимаются координатные векторы. Количество координат зависит от размерности пространства. Переходя к координатной форме для трёхмерного пространства, может быть получена следующая система параметрических уравнений:

x M = ( x A - ^XD ) ^{и +}( x B - x D ) ^{v +} ( x c - ^X D ) w ⁺ x D

< У м = ( y A - y D ) ^{и +}( y B - y D ) v ⁺ ( У С - У о ) w ⁺ У о • ⁽²⁾ , z M = ( z A - ^ZD ) ^{и +}( z B - z D ) v ⁺ ( z C - ^Z D ) w ⁺ z D

Таким образом, для определения всех параметров положения и формы ТМ параллелепипеда понадобилось 12 параметров. Если использовать для этих целей граничную модель, то количество параметров увеличивается в разы, поскольку нужно определить каждую из шести плоскостей тремя точками, а каждую точку - тремя координатами. Итого получается 54 параметра. Это только поверхность тела без учёта внутренней составляющей. Есть и другие параметризации, но для этого необходимо использовать геометрические условия, реализация которых требует дополнительных вычислительных ресурсов.

Уравнение (1) включает необходимые геометрические условия и позволяет реализовать параллельные вычисления по данным за счёт использования координатных векторов A, B, C, D, M . Все уравнения системы (2) являются полностью идентичными за исключением координат точек. Таким образом, вычислительные потоки являются сбалансированными, что минимизирует простой ядер процессора и оптимизирует его вычислительную нагрузку.

В описанной параметризации использованы линейные функции от текущих параметров u , v , w . Такие геометрические тела называются изотропными. Предложенный подход подразумевает, что для определения ТМ могут использоваться и нелинейные функции, которые управляют скоростью движения текущей точки внутри геометрического тела. Таким способом можно моделировать не только изотропные, но и анизотропные геометрические тела с функционально-управляемой анизотропией. Это открывает новые возможности геометрического моделирования физических свойств исследуемых объектов. Если под геометрическим телом понимать выделенную часть пространства, то становится возможным моделирование изотропных и анизотропных энергетических, магнитных, тепловых, световых, звуковых и других полей в виде геометрических объектов с линейной и нелинейной структурой пространства. Аналогичным образом, понимая под геометрическим телом не только твёрдые тела, можно использовать предложенный подход для моделирования физических свойств жидкостей и газов. А возможность обобщения понятия геометрического тела на многомерное пространство с учётом математического аппарата точечного исчисления позволяет использовать практически неограниченное количество параметров, описывающих соответствующие им физические свойства.

Предложенный подход к твёрдотельному моделированию представляет собой обобщение граничной и других моделей геометрических тел. Из точечного уравнения ТМ всегда в виде частных случаев можно получить уравнения поверхности оболочки путём фиксации граничных значений текущих параметров, определяющих модель геометрического тела. Например, для ТМ параллелепипеда из уравнения (1) путём фиксации граничных значений параметров u , v , w получены соответствующие грани параллелепипеда.

и = 0 ^ BCD . и = 1 ^ а // BCD .

v = 0 ^ ACD . v = 1 ^ в // ACD .

w = 0 ^ ABD . w = 1 ^ у // ABD .

Аналогичным образом можно получить каркасную геометрическую модель путём одновременной фиксации двух параметров, определив, таким образом, все 12 рёбер параллелепипеда. При одновременной фиксации трёх параметров можно получить все 8 узловых точек параллелепипеда, включая исходные точки A, B , C , D . Изменяя значения параметров от 0 до 1, можно получить точечную геометрическую модель в виде облака дискретных точек.

Следующее направление исследований - это визуализация геометрических объектов на экране компьютера. Здесь разработаны алгоритмы, благодаря которым оптимизирована визуализация существующих геометрических моделей [21-23]. В отличие от них предложенный подход к определению геометрических тел, как выделенной части пространства, позволяет разработать и реализовать новые алгоритмы рендеринга изображений для систем твёрдотельного геометрического моделирования, виртуальной и дополненной реальности. Кроме того, такой подход к моделированию геометрических тел создаёт предпосылки для разработки технологии генерации полноценных объёмных изображений в трёхмерном пространстве, основанной на генерации в трёхмерном пространстве полноценных ТМ с помощью световых лучей функционально-управляемой плотности (геометрическое тело с нелинейной структурой пространства).

Исходя из перечисленных возможностей и перспектив использования предложенного подхода к твёрдотельному моделированию, выделено три основных направления в рамках реализации стратегического проекта «Суверенные САПР»:

• ■    геометрическое ядро САПР нового поколения;

• ■    компьютерное моделирование материи и энергии;

• ■    технология генерации объёмных изображений в трёхмерном пространстве.

2 Результаты экспериментов

Предложенный подход к твёрдотельному моделированию прошёл апробацию на примере моделирования геометрических тел различной формы. Примеры моделирования геометрических тел в виде выделенной части трёхмерного пространства представлены в таблице 1.

В таблице 1: и = 1 - u , V = 1 - v , w = 1 - w - обозначение дополнений параметров u , v, w до единицы, принятое в точечном исчислении [11]. В таблице приведены только некоторые из возможных параметризаций моделей геометрических тел. Многие параметризации представлены в общем виде. Например, чтобы получить из тела трёхосного эллипсоида двухосное тело или шар, достаточно выбрать соответствующие координаты точек A, B , C , D . При этом точечное уравнение остаётся неизменным. Аналогично - с тороидальным телом. В таблице оно реализовано в общем виде, когда эллипс движется по эллиптической траектории, и соответствующими значениями координат точек модель может быть преобразована в круговое тороидальное тело.

Наряду с простыми геометрическими телами проведены вычислительные эксперименты по моделированию геометрических тел с более сложной геометрией.

Все представленные в работе ТМ визуализированы средствами компьютерной алгебры, но для этих целей могут быть использованы и другие инструменты компьютерной графики и научной визуализации.

Проведённые вычислительные эксперименты показали обоснованность и достоверность предложенного подхода.

Заключение

Предложен новый математический аппарат векторного представления геометрических объектов. Можно выделить следующие преимущества предложенного подхода и перспективы его использования в САПР:

• ■    разработка новых методов хранения геометро-графической информации, основанных на использовании точечных уравнений, инвариантных относительно параллельного проецирования;

• ■    замена некоторых булевых операций над геометрическими телами аналитическими, а воксельных моделей - векторными;

• ■    отсутствие необходимости использования матриц преобразования и согласования геометрической информации в процессе взаимодействия между CAD и CAE ;

• ■    реализация параллельных вычислений по данным на уровне математического аппарата «Точечное исчисление» и по задачам за счёт использования конструктивных алгоритмов геометрического моделирования на проективной и аффинной основе;

• ■    разработка новых методов расчёта напряжённо-деформированного состояния твёрдых тел, основанных на функционально-управляемой анизотропии и альтернативных по отношению к МКЭ;

• ■    разработка новых высокопроизводительных методов рендеринга изображений;

• ■    разработка новой технологии генерации полноценных объёмных изображений в трёхмерном пространстве.

Таблица 1 – Модели геометрических тел в трёхмерном пространстве

Наименование тела	Геометрическая схема формообразования	Точечное уравнение		Визуализация твёрдотельной модели
Треугольная пирамида	НПОС \ AW	M = Auvw + Bvw + Cuvw + Dw, u e [ 0;1 ] , v e [ 0;1 ] , w e [ 0;1 ] .		4- 3“ 2 1 о 4
Параллелепипед	CA----f--- r / По D PA	M = Au + Bv + Cw + + D ( 1 - u - v - w ) , u e [ 0;1 ] , v e [ 0;1 ] , w e [ 0;1 ] .
Треугольная призма	I        I I       XC	M = A ( uv - w ) + Bv + Cvu + Dw, u e [ 0;1 ] , v e [ 0;1 ] , w e [ 0;1 ] .
Трёхосный эллипсоид	r	M = ( A - D ) u cos 2 co + ( B - D ) u sin 2 cos + ( C - D ) u sin 9 + _ u e [ 0;1 ] , 2 е [ 0;2 ж ] , 9 e	s 9 + 9 + D , П П _ 2;2J .	6    4
Тороид	липни a       Ag	M = ( A - D ) | 1 + — u cos/ X     a + ( B - D ) [1 + —u cos 2 I     a         > + ( C - D ) u sin 2 + D u e [ 0;1 ] , 2 e [ 0;2 n ] , 9 e	. ^cos 9 + sin 9 + , [ 0;2 n ] .

Авторский вклад

Конопацкий Е.В. - общая концепция подхода к твёрдотельному моделированию и получение уравнения; Ротков С.И. - анализ существующих методов твёрдотельного моделирования; Лагунова М.В. - сравнение предложенного подхода с существующими методами твёрдотельного моделирования; Безсольнов М.В. - вычислительные эксперименты по твёрдотельному моделированию.