Поиск областей неопределенности кинетических параметров математических моделей химической кинетики на основе интервальных вычислений

Изучение механизмов сложных химических реакций на. сегодняшний день представляет огромный практический интерес. Кинетическая модель является основой математического моделирования химических реакций. Для построения кинетической модели необходимо знать участвующие в химической реакции вещества, и элементарные стадии. Традиционно при моделировании химических реакций принято использовать средние значения кинетических параметров. Моделирование химических реакций на. основе средних значений параметров не позволяет гарантировать такой режим функционирования, который может возникать в процессе эксплуатации [1]. На самом деле кинетические параметры находятся в некотором интервале возможных значений, так как определены по экспериментальным данным в ходе решения обратной задачи идентификации механизмов сложных химических реакций.

Математическое описание химических реакций представляет собой систему дифференциальных, как правило, нелинейных уравнений с заданными начальными условиями, число неизвестных которой равно числу участвующих в реакции веществ. В то же время непосредственному измерению доступна, только часть из этих веществ. Поэтому возникает обратная задача, определения параметров системы дифференциальных уравнений, воспроизводящих часть ее решений. Следствием недостаточной информативности может стать неединственность решения обратной задачи. Кинетические измерения задаются внутри некоторого интервала. точности, определяемого величиной погрешности измерений, к которым, в том числе, относятся экспериментальные концентрации в определенные моменты времени протекания реакции. Решением обратной задачи определения кинетических параметров становится некоторая область, вариация кинетических констант внутри которой сохраняет требуемое качество описания измерений.

Определить доверительный интервал в задаче математической обработки эксперимента можно методом максимального правдоподобия. В этом случае необходимо знание статистического закона распределения погрешности измерений, которое для реальных систем, как правило, отсутствует. Другая постановка расчета областей неопределенности сделана Л.В. Канторовичем [2]. Она не требует знания информации о статистических свойствах распределения погрешности измерений. Необходимо только знание величины предельно допустимой погрешности эксперимента, информация о которой чаще всего присутствует у экспериментатора. Поиск интервальных значений кинетических параметров, образующих искомую область, предполагает достаточно большой объем вычислений. Для повышения эффективности решения данной задачи наряду с высокопроизводительными параллельными вычислительными системами целесообразно использовать понятия и методы интервального анализа [3–6].

1.    Вывод математической модели

В основе составления кинетических уравнений для сложных процессов лежит положение о независимом протекании элементарных реакций [7]. В таких процессах одно и то же вещество X i может принимать участие в качестве исходного или конечного вещества в нескольких элементарных стадиях, т.е. сложная реакция может быть записана в виде:

n

^2 V ij X i = 0, j = 1,m,                                (1)

i =1

где X i – вещества, участвующие в реакции, ν ij – стехиометрический коэффициент при компоненте X i в j-й стадии, m – число элементарных стадий. Для элементарных реакций значениями ν ij могут быть только 0, 1, 2 и 3 (редко). Для итоговых уравнений таких ограничений не существует. В сложных реакциях стехиометрические коэффициенты могут быть дробные.

Скорость реакции ω i по i-му компоненту выражается изменением количества этого компонента N i в единицу времени в единице реакционного пространства. По отношению к исходным веществам такую характеристику называют скоростью превращения или расходования, по отношению к продуктам – скоростью образования.

В закрытой системе скорость гомогенных реакций –

_ 1 dN i

= Vp dt скорость гетерогенных реакций –

_ 1 dN i ^ i = FPP

где V p – объем реакционного пространства, F – площадь поверхности раздела взаимодействующих фаз.

Скорость гомогенных реакций, выраженная через концентрацию i-го компонента Ci посредством соотношения N = VC, (V — объем реакционной смеси), согласно (2), можно записать в виде:

^ i =

1 VdC i + C i dV

V p       dt

Если объем реакционной смеси при протекании химической реакции практически не изменяется (dV ~ 0), то V _p = V, и выражение (4) принимает вид:

w i =

V dC i dt ^.

Следует отметить, что это определение широко распространено в научной литературе, но не может служить в качестве общего определения понятия скорости, так как часто ока-V dC зывается, что величина dt i связана не только с числом актов химического превращения, но и с тем, по какому закону изменяется объем системы. В то же время, это изменение может осуществляться произвольным образом. На практике с протеканием газовых реакций при переменном объеме приходится сталкиваться в тех случаях, когда в реакции изменяется число молекул, а давление в системе поддерживается постоянным. Поэтому при разработке математического описания сложного процесса необходимо учитывать изменение числа молей реакционной смеси (или реакционного объема) в ходе протекания химических реакций [8]. Чтобы определить, существует ли такое изменение в ходе реакций, построим матрицу стехиометрических коэффициентов Г, элементами которой являются стехиометрические коэффициенты участвующих в реакции веществ νij . Ее строки соответствуют элементарным реакциям, а столбцы - веществам. В общем виде стехиометрическую матрицу Г можно представить:

ν 11 ν 12 ^... ν 1 m

Г _ V 21 V 22   ... V 2 m

* * *              * * *            * * *             * * *

ν n 1 ν n 2 ^... ν nm

Размерность стехиометрической матрицы n х m, где n - число веществ, m - число элементарных реакций. Стехиометрические коэффициенты веществ ν ij , исходных для данной реакции, входят со знаком « — » , продуктов реакции - со знаком « + » . Если вещество не участвует в реакции, его стехиометрический коэффициент принимается равным нулю.

Далее с помощью матрицы Г находят компоненты вектора 5 j по следующему правилу

n

5 j _ ^V ij , j = 1,m.                               (6)

i =1

Если хотя бы одна из компонент вектора δ j отлична от нуля, то реакция протекает с изменением числа молей.

Согласно закону сохранения массы (2), суммарный материальный баланс для варианта, когда суммарная концентрация C _ ^2П =1 C i изменяется во времени, имеет вид:

dC i     ^{d ( C}x i )                     q

^_   -  ^_ —r' i ^_1'n                      ⁽⁷⁾

j =1

с начальными условиями: X i (0) _ x ⁰ , где x i _ CC - концентрация i-го компонента в мольных долях, r j – скорость j-й реакции, определяемая согласно закону действующих масс. Общий вид для элементарной химической реакции:

P r _ knC A l ' l =1

где r – скорость реакции, k – константа скорости реакции, C _A ^{α l} _l – концентрация реагента A l в степени, равной стехиометрическому коэффициенту α l в уравнении реакции, P – количество исходных реагентов.

Замыкает систему уравнений (7) условие нормировки по компонентам реакционной среды:

n

^ x i ^_ 1.                                      ⁽⁸⁾

i =1

Начальная мольная плотность жидкости (начальная суммарная концентрация) C o постоянна при любых температурах. Тогда можно разделить (7) на C o . Получим систему дифференциальных уравнений

^Nx i )           ТТЛ • т

--dt-- = 2^vij Wj, i = 1,n, j=1

где N = С - относительное изменение числа молей реакционной среды, W j = j - приведенные скорости химических реакций. Обозначим

Fi = it Vij Wj, i = 1n(10)

j =i

Преобразуем левую часть системы уравнений (9), применив правило дифференцирования произведения функций и условие нормировки (8). Получим

'. = fi = F' ~ xi Fn, i = ГП,    dN = fn+1 = Fn dt           Ndt с начальными условиями:

xi(0) = x0, i = 1,n, N (0) = 1.(12)

Функции F _n , F i выписываются с учетом матрицы стехиометрических коэффициентов.

Система уравнений (11) с начальными условиями (12) является математической моделью сложной (многостадийной) реакции, учитывающей изменение числа молей в ходе ее проведения.

• 2.    Постановка обратной задачи по вычислению областей

неопределенности кинетических параметров

Классическая постановка обратных задач состоит в поиске констант скоростей реакции, минимизирующих критерий соответствия расчета состава многокомпонентной реагирующей смеси экспериментальным данным:

ns

E(k) = E Eix Rj - x Ejh                             (13)

i =1 j =1

где x _i ^R _j – расчетные значения концентраций веществ, участвующих в реакции; x _i ^E _j – экспериментальные данные; i – номер компоненты, j – номер замера; k – вектор кинетических констант; n – число веществ, концентрация которых поддается измерению; s – число замеров каждой из компонент.

Решение обратной задачи неоднозначно. Обычно это не число (точка в пространстве констант), а область, возникающая, по крайней мере, по двум причинам: 1) избыточность схемы (большое количество констант); 2) погрешность измерений. Эту область принято называть областью неопределенности. В таком случае целесообразно решать обратную задачу по определению некоторых интервалов, образующих область неопределенности, любая вариация кинетических констант скоростей внутри которых сохраняет качество описания измерений, устанавливаемое величиной, предельно допустимой погрешности эксперимента.

Применим основные понятия и методы теории интервального анализа [3, 4, 5] к решению обратной задачи по определению искомой области. Основная идея интервального анализа состоит в замене арифметических операций и вещественных функций над вещественными числами интервальными операциями и функциями, преобразующими интервалы, содержащие эти числа. Ценность интервальных решений заключается в том, что они содержат точные решения исходных задач.

Пусть γ ij – величина допустимой погрешности измерения концентрации i-го компонента в j-й замер. Тогда результатом решения обратной задачи по вычислению области неопределенности будут некоторые интервальные значения кинетических констант скоростей:

k 1 = [k 1 ; k 1 ], ..., k m = [k m ; k m ],                                  (14)

где k j , k j , j = 1,m есть нижние и верхние границы интервалов соответственно. Суть (14) состоит в том, что при решении прямой задачи (11)-(12) для V k 1 G k i , V k 2 £ k 2 , ..., V k m £ k m могут быть получены расчетные концентрации, удовлетворяющие:

^x 1j ^{£ [x} 1 j    ^Y 1 j ; ^x 1j + ^Y 1 j ^{]     x} 1 j ,   ’”’    x nj ^{£ [x} nj    ^Y nj ; x nj + ^Y nj ^]     x nj ,    j ¹, s. ⁽¹⁵⁾

Как известно, решение обратной задачи предполагает многократное обращение к решению прямой задачи. Тогда решение системы (11)-(12) с интервальными параметрами (14) приведет к интервальным значениям расчетных концентраций:

x Rj = [x Rj ; ^{x R} j 1, -, x R = ^[x ^R j ; x ^Rj 1, j =TTs-                      ⁽¹⁶⁾

Тогда требуется найти такие интервальные значения кинетических констант скоростей реакции (14), что ns

^{Q( k )} = ^^ q ^{( x R} , ^x E ) ^ ^{min,                       (17)}

i=1 j=1

где q(x R , x E ) = max {| x R — x E | , | x R — x E |} - расстояние между двумя интервалами, k -интервальный вектор кинетических констант.

• 3.    Алгоритм решения прямой задачи методом интервального анализа чувствительности

Для решения задачи (11) – (12) в условиях (14) будем использовать модифицированный метод интервального анализа чувствительности, ранее описанный в работе [6]. Основная идея метода заключается в анализе частных производных решения по параметрам. Для его реализации используется аппарат интервального анализа. Запишем задачу (11) – (12) в виде системы обыкновенных дифференциальных уравнений:

dx- = f i (t,^x,^k), i = ^1,n, n = q + ^1,

где q – количество веществ, вступающих в реакцию, xi(0) = xoi, i = 1,n — 1; xn(0) = xon = N (0) = 1.                  (19)

Будем искать решение системы (18) с начальными условиями (19) в виде x = ( x ⁽¹⁾ , x ⁽²⁾ ,..., x ⁽ⁿ⁾ ), где x ⁽ⁱ⁾ = [x i ,x i ], x i - нижняя и x i - верхняя границы соотвествующего интервала. Аналогичное представление характерно для вектора констант скоростей (14).

Пусть требуется оценить x ⁽ⁱ⁾ - верхнюю границу решения по i-й координате. Для ее оценки система уравнений (18) с начальными условиями (19) примет вид:

′ x = f(t,x,k), k £ k,     x(0) = xo £ xo-                       (20)

Здесь kj = < kj, kj, -kj, если xkj (t) < 0, если xkj- (t) > 0, если xkj (t) 9 0, (21) X0j, если xj (t) < 0, x0j = * x0j, если xj (t) > 0, (22) - x0 j, если xkj (t) 9 0, где xkj (t) — интервальное расширение dxj и x0j (t) — интервальное расширение d^ij. Если интервалы xkj (t), xj(t) не содержат в себе нуль, то система (20) не содержит интервальных параметров и решается интервальными или двусторонними методами с произвольной точностью [9].

Интервальные функции x kj (t), x j (t) можно определить, одновременно решая (18)-(19)

и систему вида:

x kj' = ^ df i (t,x,k)x kj + f(t,x,k),                       (23) i =i XXl                  j x k = 0, i = 1,n, j = 1,m,                             (24) x 0 j = ^ df i (t, x, k)x ij' ,                                    (25) l =1 x l 0 x     S 1, при i = j ,    • • i x j = O ij = <          .         i,j = 1,n-                           (26) [0, при i = j;

Совместное решение (18) – (19), (23) – (26), равно как и системы (20), можно получить приближенным явным методом Рунге–Кутты 4-го порядка точности. При этом решение системы дифференциальных уравнений проводится на основе алгоритма нахождения интервальных расширений для полиномиальных функций.

Оценка нижней границы решения по i-й координате x ⁽ⁱ⁾ проводится аналогично с соответствующими корректировками, вытекающими из соображений достижения минимума функции на границах получаемых интервалов.

Метод интервального анализа чувствительности дает возможность определения такого момента времени t opt > 0 [6], до которого найденные границы множества решений (18)-(19) могут считаться оптимальными.

Существуют иные подходы к построению двустороннего решения (18) - (19). Так, в [10] на примере реакции с постоянным реакционным объемом рассмотрен метод, основанный на понятиях монотонности, изотонности функций по переменным и приводящий к представлению исходной системы в виде двух независимых подсистем, параллельное решение одной из которых дает нижнюю, другой – верхнюю границы интервального решения (18) – (19).

4.    Алгоритм интервального решения обратной задачи по определению констант скоростей

Процедура решения обратной задачи по вычислению областей неопределенности кинетических констант состоит в поиске интервальных значений констант скоростей стадий, минимизирующих функционал (17). Для минимизации функционала (17) будем использовать модифицированный под интервальные вычисления метод Хука – Дживса, который представляет собой комбинацию исследующего поиска с циклическим изменением переменных и ускоряющего поиска по образцу. Сформулируем алгоритм поиска кинетических констант по шагам.

Шаг 1. Ввод исходных данных: t - время протекания реакции, x (0) — вектор начальных концентраций, x ^E – матрица интервальных значений экспериментальных концентраций в фиксированные моменты времени, ε – минимальное значение функционала (17) (критерий остановки поиска), h j – шаг вариации по границам каждой координаты (константы скорости), e j – минимально допустимое значение шага вариации по границам каждой координаты в ходе исследующего поиска, imax – максимальное количество итераций поиска, k _j ^down , k _j ^up – величины, образующие область поиска (нижний и верхний предел соответственно); j = 1,m, m - количество констант скоростей.

Шаг 2. Задается стартовая точка (начальное приближение) k ^j = ( k j , k 2 ,..., k m ), где k j = [k j ; k j ]. В качестве начального приближения может быть выбран вектор вырожденных интервалов. Номер текущей координаты s = 1. Номер итерации поиска i = 0. Вычисляется значение функционала Q( k ^j ).

Шаг 3. Проводится решение прямой задачи при четырех наборах кинетических параметров:

kj+ = (kj, k2>..., [kj + hs; Й>-> km) при kj + hs < kup, ks— = (kj, k2>-> [kj — hs; Й>-> km) при kj - hs > kdown, kj+ = (kj, k2,..., [kj; k1 + hs],..., km) при kj + hs < ku, ks- = (kj, k2,..., [kj; kj - hs],..., km) при kj - hs > kdown.

Варьирование границ на данном шаге алгоритма также сопровождается контролем выполнения условия ≪ непересечения ≫ верхней и нижней границы текущей координаты. Вычисляются значения функционала Q( k ^j ₊ ), Q( k ^j_ ), Q( k j+ ), Q( k j^ ) при заданных наборах параметров.

Шаг 4. Если Q( k ^j ) < Q( k ^j ₊ ), Q( k ^j ) < Q( k ^j- ), Q( k ^j ) < Q( k s + ), Q( k ^j ) < Q( k s — ), то шаг h s уменьшается с переходом на Шаг 3. Уменьшение h s на этом шаге алгоритма ограничивается минимально допустимым значением e _s . При отсутствии возможности уменьшать шаг далее текущая координата не изменяется. В противном случае k ¹ заменяется на один из векторов k _s ¹ ₊ , k _s ¹ _- , k _s ¹ ₊ , k _s ¹ _- , соответствующий минимальному из значений функционалов.

Шаг 5. Если s < m, то s = s + 1 и переход на Шаг 3. Иначе путем исследующего поиска по границам всех координат (Шаг 2 – Шаг 4) получаем новый набор констант k ² = ( k j , k 2 ,..., k m ). Если условия окончания алгоритма Q( k ) < е или количество итераций поиска, равное установленному максимальному значению i, не выполняются, то переход на Шаг 6.

Шаг 6. Начинается поиск по образцу. Проводится расчет нового набора констант по формуле k ³ = k ^j + c ( k ² - k ^j ), где c – параметр алгоритма. Обычно выбирается равным 2. В случае интервальных вычислений c = [2; 2] - вырожденный интервал.

Шаг 7. Исследующий поиск (Шаг 2 – Шаг 4) для нового набора констант k ³ , за исключением того, что шаги вариации по константам h _s на этом этапе метода не уменьшаются. В результате получается набор констант k ⁴ = ( k j , k 2 ,..., k m ).

Шаг 8. Если вектор k ⁴ отличен от k ³ , то осуществляем замену k ^j = k ² , k ² = k ⁴ , i = i+1 и переход на Шаг 6. В противном случае k ^j = k ² , i = i + 1 и переход на Шаг 3 к исследующему поиску.

5.    Вычислительный эксперимент

Проведем вычислительный эксперимент по решению обратной задачи определения области неопределенности констант скоростей на примере промышленно значимой реакции олигомеризации α-метилстирола. Продукты реакции являются ценным нефтехимическим сырьем и используются в качестве диэлектрических жидкостей, основы смазочных масел, пластификаторов каучуков, реактивного топлива, изоляционного материала, стойкого к радиолизу теплоносителя [11]. Введем обозначения для веществ, участвующих в реакции: X i -α-метилстирол; X 2 – 4-метил-2,4 дифенилпентен-1; X 3 – 4-метил-2,4 дифенилпентен-2; X 4 – 1,1,3-триметил-3-фенилиндан; X 5 – тримеры. Реакция является многостадийной и протекает в условиях изменения количества молей реакционной среды. Экспериментальные данные получены в лаборатории приготовления катализаторов Института нефтехимии и катализа РАН [12].

В результате решения обратной задачи был найден набор параметров k ¹ = (k 1 ,..., k]^), при котором наблюдается наименьшее отклонение между расчетными и экспериментальными значениями концентрации веществ, участвующих в реакции. В табл. 1 представлены начальное приближение поиска области неопределенности и интервальный вектор констант скоростей, образующий искомую область.

Таблица 1

Константы скоростей, полученные в ходе решения обратной задачи

Константа скорости	Начальное приближение k 1	Интервальное решение k ⋆
k 1	1,19575	[ 1,00825; 1,38325 ]
k 2	0,12781	[ 0,10613; 0,14656 ]
k 3	0,19794	[ 0,17294; 0,23525 ]
k 4	0,02630	[ 0,02318; 0,02552 ]
k 5	0,06974	[ 0,06896; 0,06974 ]
k 6	0,49184	[ 0,47934; 0,50590 ]
k 7	0,00001	[ 0,00020; 0,00040 ]
k 8	0,41116	[ 0,40178; 0,41116 ]
k 9	0,07412	[ 0,07295; 0,07373 ]
k 10	0,00001	[ 0,00001; 0,00176 ]
k 11	0,00649	[ 0,00478; 0,00493 ]
k 12	0,00001	[ 0,00001; 0,00001 ]

Интервальное решение обратной задачи получено в ходе минимизации критерия отклонения расчетных и экспериментальных значений концентраций x R и x E (i = 1, 5 - количество веществ, j = 1, 7 - количество замеров), представленных в табл. 2. Компоненты интервальной матрицы экспериментальных концентраций представляют собой интервалы, содержащие 10%-ную погрешность от значений концентраций, соответствующих решению прямой задачи для набора параметорв k ¹ .

На рис. 1 – рис. 3 представлена динамика изменения концентраций трех из пяти веществ, участвующих в реакции: точками • обозначены данные эксперимента, □ - верхние и нижние границы интервальных компонентов матрицы экспериментальных данных x _i ^E _j , сплошной линией – результаты решения прямой задачи при наборе констант скоростей k ¹ ,

Таблица 2

Концентрация компонентов, мол. доли t, ч x1E x2E x3E x4E x5E 0 [1; 1] [0; 0] [0; 0] [0; 0] [0; 0] 0,5 [0,3617; 0,4421] [0,3553; 0,4343] [0,0565; 0,0691] [0,0689; 0,0842] [0,0578; 0,0707] 1 [0,1608; 0,1965] [0,4110; 0,5024] [0,0984; 0,1203] [0,1013; 0,1238] [0,1287; 0,1573] 2 [0,0547; 0,0669] [0,3521; 0,4303] [0,1518; 0,1855] [0,1458; 0,1782] [0,1958; 0,2394] 3 [0,0279; 0,0341] [0,2812; 0,3436] [0,1801; 0,2201] [0,1884; 0,2303] [0,2228; 0,2723] 4 [0,0182; 0,0222] [0,2227; 0,2721] [0,1921; 0,2348] [0,2302; 0,2814] [0,2371; 0,2898] 5 [0,0141; 0,0172] [0,1760; 0,2151] [0,1934; 0,2363] [0,2701; 0,3301] [0,2467; 0,3015] пунктирной линией – результаты решения прямой задачи, полученные для интервалов констант скоростей k⋆ . Вариация кинетических констант в пределах полученных интервалов неопределенности k⋆ не изменяет динамику кинетических кривых. Выход основных продуктов реакции чувствителен к такой вариации в среднем, не более, чем на 10 - 12%. Это означает, что любой набор кинетических параметров, принадлежащий области неопределенности по компонентам вектора констант k⋆ , приводит к решению прямой задачи, неизменно лежащему в пределах границ интервального решения. При этом значения расчетных концентраций веществ находятся в пределах допустимой погрешности эксперимента. Следует отметить, что полученное интервальное решение прямой кинетической задачи в условиях интервального решения к* будет оптимальным до момента topt = 0,45 ч.

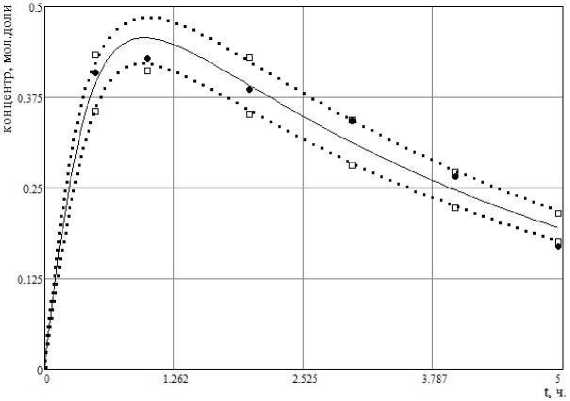
Рис. 2 . Расчетные и экспериментальные концентрации X ₂

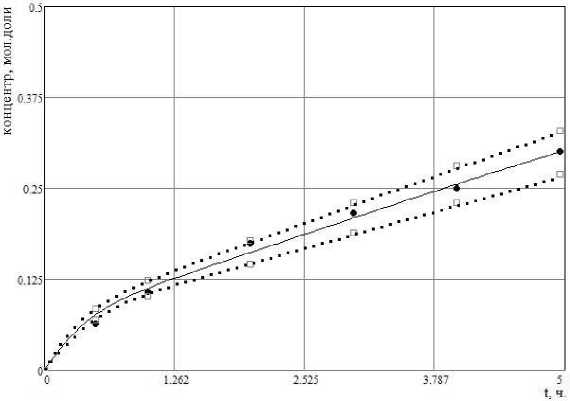
Рис. 3 . Расчетные и экспериментальные концентрации X ₄