Полиномиальные уравнения Вольтерра I рода в задаче моделирования нелинейных динамических систем с обратной связью

В теории моделирования систем управления традиционно используется аппарат дифференциальных уравнений. Тем не менее разработка альтернативных методов моделирования, связанных с приложением интегральных уравнений типа Вольтерра, является актуальной прикладной задачей (например, [1, 2]).

Как известно, одним из наиболее универсальных методов математического моделирования нелинейных динамических систем типа черного ящика является представление отклика системы y ( t ) на входной сигнал x ( t ) в виде полинома Вольтерра. Полином Вольтерра N -й степени, отображающий x ( t ) в y ( t ) , имеет вид

N

y ( t ) = ∑ ∑     f i ₁,..., i_n ( t ), t ∈ [0, T ],                  (1)

n = 1 1 ≤ i ₁ ≤ ... ≤ i_n ≤ p

Работа выполнена при поддержке гранта РФФИ № 09-01-00377.

где tt f',...^ (t) = J ...J K^..^ (t, sp..., sn )П Х,Д Sj) dSj, t e [0, T ],(2)

t имеет физический смысл времени, x ( t ) = ( x ₁( t ),..., x p ( t )) есть p -мерная вектор-функция времени, у ( t ) - скалярная функция времени, причем у (0) = 0, у ‘ ( t ) e С _[0 , _T ] . Ядра Вольтерра К_ц ii в (2) симметричны лишь по тем переменным, которые соответствуют совпадающим индексам. При построении модели (1), (2) в теории динамических систем надо уметь находить ядра Вольтерра. Для решения этой задачи можно использовать метод [3, 4], основанный на задании специальных тестовых входных сигналов.

Предположим далее, что задача идентификации ядер Вольтерра K i i в (2) решена. Будем считать также, что возмущения x , ( t ), i = 2, p в (2) известны. Помимо нужной гладкости исходных данных в (1), (2) будем предполагать, что K ₁( t , t ) * 0 V t e [0, T ]. Рассмотрим наиболее интересный для приложений случай N = 2 в (1). В случае стационарной динамической системы вместо (1), (2) имеем p             p              p i - 1

i V 1,i X i + i V 2,i x + i! V 2, ji ( X j ,X i ) = у ( t ), t e [0, T ],        (3)

i = 1              i = 1                i = 2 j = 1

t

Vvx = J ^k - ⁽ t ^- s ) X⁽ s ) ds , 0 tt

• V 2, - X-² = JJ K и ( t - S 1 , t - S 2 ) X , ( S 1 ) X , ( S 2 ) dS 1 ds 2 , 00 tt

• V 2, ji ^{( x} - , ^Xj ) = JJ K ji ⁽ t ^{- s} 1 , t ^{- s} 2 ) ^Xj ^{( S} 1 ) X ^{( s} 2 ) ^ds 1 ^ds 2 , i * j ; i , j = ¹, p .

Рассмотрим задачу стабилизации (регулирования), связанную с поиском управляющего воздействия x ₁ ( t ), поддерживающего выходной сигнал у ( t ) на заданном уровне у * . Такая постановка возникает в связи с задачами автоматического управления техническими объектами. В этом случае уравнение (3) является полиномиальным уравнением Вольтерра I рода, непрерывное решение которого, вообще говоря, носит локальный характер. В работах [5-8] приведены результаты в области теории и численных методов построения непрерывных решений полиномиальных уравнений (при N = 2,3 в (1)) для случая, когда x ( t ) - скалярная функция времени.

1.    Постановка задачи

В работе [9] рассмотрена численная схема решения полиномиального уравнения (3) для p = 2 при условии отсутствия обратной связи. Развивая исследование, начатое в [9], рассмотрим алгоритм получения управляющего воздействия x1 (t) с учетом апостериорных данных об отклонении выходной переменной у (t) от желаемого значения у *, так что x1(t) = u(t- h), u(^) = 0, ^e [-h,0], h - известное постоянное запаздывание. В этом случае задача регулирования нелинейного динамического объекта сводится к поиску непрерывного решения u* (t) полиномиального уравнения Вольтерра I рода pp

• V1,1u + Z V1,ixi +Z V2,1i (u, X) + V2,1 u 2 + i=2

2.    Полиномиальные уравнения Вольтерра I рода

pp i

+Z V2,ix + ZZ Vj Xj, Xi) = f (t),(4)

i = 2               i = 2 j = 2

где f ( t ) = Л t ) - Л t - h ), t e [0, T ].   Сигнал ^ ( t ) = у * - у ( t ), e ( ^ ) = 0,

^e [ - h ,0] считаем рассогласованием или ошибкой управления.

Чтобы понять специфику полиномиального уравнения (3), рассмотрим случай постоянных ядер: K i = k i , k 1 >  0, K ji = k i , 1 <  j <  i <  p . Все функциональные пространства считаем вещественными.

Не уменьшая общности, зададим к 1 = 1, так что (3) принимает вид

t

t

pt

1 + Z k i i j x i ( ^s ) ds J x 1 ( s ) ds + k 11 J x 1 ( s ) ds

i = 2      0

_ 0

к 0

= f ( t ),    t e [0, T ],

У

где

pt                  p f (t) = у (t) - Z ki J Xi( s) ds - ZZ kji J Xi (s) ds  J Xj (s) ds .

t

i

t

t

Л

i = 2     0

Теорема 1. Пусть

i = 2 j = 2

к 0

Ук 0

У

f ( t ) e C^_T ] , f (0) = 0.

Тогда решение (5), (6) определяется формулой

x ( t ) =

f ‘ ( t )

У

+— в ( t ) —( 1 + в ( t ) ) - 11, a ( t )   2 k 11      к a ( t ) ⁽ J

к ^{а (} t )

где

t ei (t) = J xi (s)ds, i = 2, p ,

p

в( t) = Z ki iei (t), i=2

a (t ) = ^( 1 + в ( t ) ) 2 + 4 k ii f ( t ).

Доказательство. Убедимся, что подстановка (8)-(11) в (5) обращает его в тождество. Имеем:

t                      i - ^{e (} t) +« ⁽ t ) i

I = [ x ^; ( s ) ds = — f du = —(-£ (t ) + a (t ) - 1 ) ,     (12)

₀             2 k _{11 1}           2 k ₁₁

отсюда, с учетом (9)-(11), p t

1 + Z k i i J x ( s ) ds I + k ii 1 ² = f ( t ).

i = 2      0

Теорема 1 доказана.

Замечание 1. Условие f (0) = 0 использовалось для вычисления в (12)

нижнего предела интегрирования, соответствующего замене и = -в ( s ) + а ( s ).

Для установления принадлежности решения к классу C _{[0, T ]} нужны дополнительные предположения, обеспечивающие строгую положительность подкоренного выражения в (11).

Убедимся, что в некоторых случаях непрерывное решение уравнения (5), (6) носит глобальный характер. Следуя [6], рассмотрим следующую теорему.

Теорема 2. Пусть f (t) знакопостоянна на [0,T] . Если при этом sign ku = sign f (t), то

x ; ( t ) e c _[0 T ] v t < ^ .

Доказательство немедленно следует из (8) – (11).

Теорема 2 доказана.

Заметим, что в линейном случае условие у (0) = 0 гарантирует отсутствие решений в классе обобщенных функций. Следующая теорема показывает, что при переходе к (5), (6) это заведомо не так.

Теорема 3. Если x ; ( t ) - решение уравнения (5), (6), то

( .             1 _            1

x ;^; ( t ) =-

x i ⁽ t ) ⁺ —5⁽t ) ⁺—Z k i i x ⁽ t )

V k 11 k ii ¹=2

также решение (5), (6). Здесь 5 (t ) есть 5 - функция Дирака.

Доказательство. Покажем, что подстановка (13) в (5) обращает его в тождество. Действительно, в силу (13)

t-                    11      t-

I = j x f* ( s ) ds = - j x f ( s ) ds ----E k J x ( s ) ds ,

^J0                0              k 11 k 11~ ¹ i 0 i'

следовательно pt

¹ + E k u J x ^{( s} ) ^ds

I + k_n 1 ² =

i = 2      0

p

1 + E к i i = 2

J x i ( s ) ds J x f ( s ) ds + k_n

tt

0 J 0

J x ( s ) ds k 0          7

- f ( t ),

поскольку x f ( t ) - решение (5), (6).

Теорема 3 доказана.

Единственность решения (5), (6) в классе С[0 T] обеспечивает следую- щая теорема.

Теорема 4. Если решение (5), (6) в С _[0 , T ] существует, то оно единственно.

Доказательство. Сделаем противоположное предположение, что существуют два решения x f ( t ), x f* ( t ) * x f ( t ), принадлежащие C _{[0 T} ] . Тогда разность x f ( t ) - x f* ( t ) удовлетворяет тождеству

u(t) J (xf (s) - xf* (s))ds - 0, t e [0, T], где

u ( t ) = 1 + в (t ) + k_n J ( x f ( s ) + x f* ( s )) ds .            (14)

В силу непрерывности x f ( t ) и x f* ( t ) значение u ( t ) в (14) не может тождественно равняться нулю, так как и (0) = 1. Следовательно,

J (xf (s) - xf* (s))ds - 0, t e[0, T], а значит, xf (t) - xf* (t), что противоречит предположению.

Теорема 4 доказана.

3.    Мажорантные уравнения

Предположим далее, что допустимые входные возмущения есть x, (t) g X , = {Xie(t), Xi g R, t g [0, T]}, i = 2, p, здесь e(t) - функция Хевисайда.

По аналогии с [5-8], рассмотрим мажорантное интегральное уравнение для (5), (6) в виде

p

1 - tYM^L

1 ii

V       i = 2

t

J ^ ( s ) ds - M 11

f t

J ф ( s ) ds

V 0        7

pi

= Ft + 1 ² ii M j, L , L i , i = 2 j = 2

где

M , = | ^ , | >  0,    L , = A i l >  0, M ,i= | k ,i | >  0, 1 <  j <  i <  p ,

p

^F = F + £ M i L , F = maxi y ^,( t )| >  0.

i = 2                     < <

Заменой вида (9) решение уравнения (15) может быть сведено к нахождению решения задачи Коши

F + 2 t £ i.M„L,L,+ 6 t i „L i

6( t ) =---------------- _p----------- , 6 (0) = 0, t g [0, T ]     (16)

1 - 2 M u6( t) -1^M 1L i=2

и его дифференцированию. Так как замена вида (9) сводит (15) к квадратному относительно 6(t) уравнению ppi

1 - 1 i M 1 i L | 6 ( t ) - M 11 6 ( t )² = Ft + 1 ² ^^ M ji L j L i ,

V       i = 2          7                                      i = 2 j = 2

то его решение, удовлетворяющее условию 6(0) = 0, имеет вид где

x ⁽ t ) =

6 * ( t ) =

1 f       ^р

— 1 ^- t i M 1 , l - x ( t )

11 V       i = 2

p 2 t i M 1i L- 1 1

V i = 2              7

- 4 tM 11

'

I ² + 1 ii M , v         i = 2 , = 2              7

Ясно, что (17), (18) и является точным решением мажорантной задачи Коши (16).

Таким образом, если исходным данным в (5), (6) отвечает набор ( F , M i , M ,i , L i ), 1 <  j <  i <  p , то непрерывное решение уравнения (5), (6)

x f ( t ) заведомо существует и единственно на [0, T ], где

ɶ

p т < т• = _ £M 1 iL + 2M 11 F - 2у|, nV t2                у

Y = M_пF £ M_uLi + M_пF I + M _п££ Mj ,

( р

ɶ

pi

V i = 2

( р Л²

п = £ M А V i = 2

У          i = 2 j = 2

pi

- ⁴ M 11 ££ м^, i = 2 j = 2

причем справедливо неравенство

| х (t )| < ф (t), t е[о, т *), где, с учетом (18), (19), ф (t) =----1----

2 M _п х ( t )

pp

У M_UL - tn + 2 FM_n--£M_uL_t .

1 i i                            11                                  1 i i

V i = 2                         У ² M 11 i = 2

4.    Численный алгоритм учета обратной связи

Допустим, что численное решение полиномиального уравнения (4) существует. Найдем его кубатурным методом средних прямоугольников.

Введем сетку узлов ti = ih, t 1 = i— 2

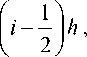
i = 1, n , nh = T . Аппроксими- руем интегралы в (4) суммами. Для нахождения аппроксимации u; (t) в

i

-м узле получим квадратное уравнение относительно u

h

1 •

i—

У

У

h 2 K

u

h

i

V

i -

i

+ h к 1 1 + 2 h £ к 11

V

j = 2

2, ^j

u

i—

h

p

i

\

у

= f (h - z(ih) — h £ K 1

i

i -

где

p

i

j = ² V

j

I—

+ h £ K 11

к = 2

^{j -}? ^к-

uh

с—

i - к + ¹

+ h ££ к 1

А = 2 к = 1

¹ А 1 , 2, ^к

x

г —

h

' А

1        1

i - к +-

u

h

² У

i—

p

i

+ h ££ к 1 А

А = 2 к = 1

' 1,1

^{j -} 2 ^{к -} 2

h

ХА i - к+

uh

i - j + 1 2

, (20)

z ⁽ ih ) = h ££ ^к а 1

i

i

у

А = 2 j = 1 V

j

I—

i

+ h£K_uu

АА

к = 1

^{j -} 2, ‘-

г —

h

^Х А

1 , 1

i - к +-

А - 1

i

У ( lh ) = h £ к 1 _а + h £ к 11

j = ² V

к = 2

^{j -} 2, ‘-

u

г —

h

p

i

I - к-

+ h ££ K vА

+ h ££ к 1

А = 2 к = 1

h

v = 2 к = 1

¹ А. 1 , ^{j -} _? ^к

г —

h

^Х А

■ 11 ^{j -} -, i.

^X v

г —

- к + 1

² у

xh

^А - - j ■

,

■ , 1

i - к +—

2 У

u

h

i - 7 — 2

z ( lh ),

y ( h ) = z ( h ), f ( h ) = £ ( h ), f ( lh ) = £ ( lh ) - £ (( l - 1) h ), ^ ( ih ) = y *- y ( ih ), l = 2, n .

Выбор нужного корня в (20) определяется условием

u 1 ^h

h - 0

■> U (0) =

y '(0)

K 1 (0)

Дальнейшее развитие работы связано с исследованием нелинейных процессов теплообмена. В качестве эталонной динамической системы будет рассмотрена математическая модель переходного процесса в элементе теплообменного аппарата, предложенная в [10].

Заключение

В работе исследуется один класс нелинейных интегральных уравнений Вольтерра I рода, связанный с задачей моделирования нелинейной динамики в векторном случае. Разработан адаптивный алгоритм учета обратной связи для применения полиномов Вольтерра в задачах автоматического управления нелинейными динамическими системами типа черного ящика. Для установления области существования непрерывного решения применена техника получения неулучшаемых оценок решений нелинейных интегральных неравенств, разработанная в [5–8]. Также показано, что, несмотря на условие у (0) = 0, данные полиномиальные уравнения Вольтерра I рода заведомо имеют решение в классе обобщенных функций.