Понятие и критерии емкостного типа некомпактного риманова многообразия на основе обобщенной емкости
Автор: Кесельман Владимир Михайлович
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика и механика к 75-летию проф. В.М. Миклюкова. Часть I
Статья в выпуске: 2 т.22, 2019 года.
Бесплатный доступ
Вводится достаточно общее понятие интегральной емкости на римановом многообразии, которое включает в себя основные классические для геометрической теории функций емкости, в том числе конформную емкость. В терминах этой обобщенной емкости, как и в классике, определяется понятие типа (параболический, гиперболический) некомпактного риманова многообразия. Приведены интегральные критерии емкостного типа некомпактного риманова многообразия. Их частными случаями являются известные критерии конформного типа риманова многообразия.
Риманово многообразие, емкость, конформный тип, p-параболический тип, p-гиперболический тип, объем геодезического шара, площадь геодезической сферы, функция исчерпания
Короткий адрес: https://sciup.org/149129856
IDR: 149129856 | УДК: 517.95 | DOI: 10.15688/mpcm.jvolsu.2019.2.2
Текст научной статьи Понятие и критерии емкостного типа некомпактного риманова многообразия на основе обобщенной емкости
DOI:
1. Обобщенная емкость и емкостной тип некомпактного риманова многообразия
Всюду в работе рассматривается произвольное п-мерное (п > 2) гладкое связное риманово многообразие, обозначаемое через М п или просто М .
Понятие типа риманова многообразия опирается на понятие емкости его компактного подмножества. Мы вводим достаточно общее понятие интегральной (или вариационной) емкости компакта на римановом многообразии, включающее в себя основные классические для геометрической теории функций емкости, в том числе так называемую конформную емкость. Базой такого определения емкости для нас были работы Г. Шоке [9] (где рассмотрена общая концепция емкости), В.Г. Мазьи [5] (где вводится и используется обобщенная емкость для множеств в R ” ) и В.М. Миклюкова [6] (в которой обобщенная емкость применяется на римановом многообразии). В данной работе в определении емкости мы придерживаемся подхода В.Г. Мазьи.
1.1. Понятие (F,p)-емкости компакта на римановом многообразии
Пусть F = F(х, £,) — какая-либо гладкая неотрицательная функция, где (х, £,) G G ТМ п , обращающаяся в ноль только при L = 0 и удовлетворяющая следующему условию: для любых х G М п , L G Т ж М п , Л G R выполняется неравенство
F(х, Л^ < c F | Л | F(х, ^)
с некоторой постоянной c F > 1, не зависящей от х, ^ и Л.
Такую функцию F будем называть допустимой для (F,p) -емкости , в связи со следующим ниже определением (F,p)-емкости.
Фиксируем произвольно число p > 1. Назовем (F,p)-емкостью компактного множества К С Мп число capF,p К := inf
j (F(х, V u)) p dv,
где точная нижняя грань берется по всем локально липшицевым функциям и, финитным в М п и таким, что и > 1 на К. (Здесь градиент V u и элемент объема dx связаны с исходной римановой метрикой многообразия М п .)
Отметим, что более правильно емкость cap Fp K следовало бы называть (F, p)-емкостью компакта К относительно абсолюта многообразия М п , поскольку ее значение зависит от «массивности» идеальной границы (абсолюта) многообразия.
Частные случаи (F,p)-емкости
В классическом случае, когда F(х, ^) = | ^ | , введенная (F,p)-емкость (2) называется p -емкостью , а при p = п — конформной емкостью .
В монографиях [5] и [6] в определении (F, p)-емкости предполагается, что функция F является однородной первой степени по переменной ^, то есть для любых (х, £,) G G ТМ п и Л G R выполняется равенство
F (х, Л ^) = | Л | F (х, ^).
Значит, в этом случае условие (1) выполняется с постоянной c F = 1.
В классическом случае p-емкости функция F удовлетворяет, помимо основного условия однородности (по переменной ξ), еще и «неравенству треугольника» (аксиоме нормы) по аргументу ξ. Ниже, в теореме 1, нам потребуется более слабое неравенство («обобщенное неравенство треугольника»):
F(х, ^ + ^ 2 ) < C F (F(х, ^ 1 ) + F(х, ^ 2 )) (3)
для любых х G Мп, ^ 1 G Т ж Мп, ^ 2 G Т ж М п .
Наряду с классическим случаем p-емкости в качестве F(х, ^) могут выступать любые нормы в пространстве Т ж М п . Более того, эти примеры (F,p)-емкости, как показывает следующее замечание, можно существенно расширить.
Замечание 1. Гладкая функция F = F(х, £,), (х, ^) G ТМ п , будет допустимой для (F,p)-емкости, если справедливы неравенства:
У(х, ^) G ТМп : ci/(х)||^||ж < F(х, ^) < C2/(х)||^||ж с некоторыми постоянными с1 > 0 и с2 > 0, не зависящими от ж и ^.
Здесь || • Цх — какая-либо норма в пространстве Т х М п , а f = /(ж), ж G М п , — произвольная положительная функция на М п .
Такая функция F удовлетворяет также и «обобщенному неравенству треугольника» (3). При этом в качестве постоянной с F можно взять с р = с 2 /с 1 .
Основные свойства емкости
Введенная (F, р)-емкость обладает следующими свойствами.
Монотонность емкости. Для любых компактных множеств К 1 и К 2 , таких, что К 1 с К 2 , справедливо неравенство:
cap F,p К < cap F,p К.
Непрерывность емкости. Для компакта К с М и произвольного числа г > 0 существует такая окрестность U с М компакта К, что для всех компактов К, таких что К с К с U, верно неравенство cap Fp К < cap F,p К + г .
Неравенство Шоке. Для любых компактных подмножеств К 1 и К 2 многообразия М выполняется следующее неравенство:
cap F,p К U К + cap F,p К cap К < cap F,p К + cap F,p К 2 .
Функция компактных множеств, удовлетворяющая приведенным здесь свойствам, называется емкостью Шоке .
1.2. Понятие (F,p)-емкостного типа риманова многообразияДалее предполагается, что многообразие Мп является некомпактным.
Будем говорить, что многообразие М п имеет (F,p) -параболический тип , если cap F,p К = 0 для любого компакта К с М п .
В противном случае (то есть если cap F,p К > 0 для какого-либо компакта К с М п ) будем говорить, что многообразие М п имеет (F,p) -гиперболический тип .
В случае p-емкости это определение совпадает с общеизвестным определением р- типа (при р = п — конформного типа) риманова многообразия М п .
Хорошо известно, что в определении р-параболического типа многообразия выполнение условия обращения в нуль p-емкости компакта К достаточно требовать лишь для одного невырожденного континуума (под которым понимается, как обычно, связное отличное от точки компактное множество).
Аналогичный факт имеет место и для принятого нами понятия (F, р)-параболи-ческого типа многообразия в случае, когда допустимая для (F,p)-емкости функция F удовлетворяет еще «обобщенному неравенству треугольника».
Теорема 1. Пусть допустимая для ( F^ ) -емкости функция F удовлетворяет условию (3). Предположим, что cap Fp К = 0 для некоторого невырожденного континуума К с Мп. Тогда cap F,p K = 0 для любого компакта К с Мп.
Следствие 1. Предположим, что допустимая для (F,p') -емкости функция F удовлетворяет «обобщенному неравенству треугольника» (3).
Тогда многообразие Мп имеет (F,p'} -параболический тип в том и только том случае, когда cap F,p К = 0 хотя бы для одного невырожденного континуума К .
Соответственно, Мп имеет (F,p'} -гиперболический тип в том и только том случае, когда cap F,p К > 0 для любого невырожденного континуума К с Мп.
2. Критерии (F,p)-емкостного типа некомпактного риманова многообразия
В данном разделе для введенного понятия (F,p)-емкостного типа многообразия Мп мы распространяем полученные в совместной с В.А. Зоричем работе [2] критерии конформного типа (то есть когда F(х, ^) = | ^ | , р = п) некомпактного многообразия М п , выраженные в виде условий на рост объема V(г) и площади S(г) граничной сферы геодезического шара радиуса г в полной метрике, конформно-эквивалентной исходной метрике многообразия.
В предлагаемых критериях (F,p)-емкостного типа многообразия роль класса конформных полных метрик принимает на себя класс функций исчерпания данного многообразия, играющих роль функции геодезического расстояния г на полном некомпактном многообразии.
В свою очередь, роли функций объема V(г) и площади S (г) сферы геодезического шара радиуса г играют, соответственно, вводимые ниже величины обобщенного объема V F,p,h (г) и обобщенной площади S F,p,h (r).
Дадим сначала точные определения названных понятий: функции исчерпания многообразия, а также обобщенной площади и обобщенного объема.
2.1. Функция исчерпания многообразия и связанные с нею обобщенные площади и объeмы
Для функции h Е С(М, R) и ее значения t Е R введем обозначения множеств
B h (t) := { х Е М : h(x) < t } , E h (t) := { х Е Мп : h(x) = t } , которые естественно называть, соответственно, h -шаром и h -сферой (радиусов t) на многообразии М .
Функцией исчерпания многообразия М назовем такую локально липшицеву неотрицательную и неограниченную в М функцию h, что семейство открытых шаров B ^ (t), t > 0, образует исчерпание многообразия М , то есть все эти h-шары предкомпактны, B h (t 1 ) b B h (t 2 ) при любых t 1 < t 2 , причем U t B ^ (t) = М .
Очевидно, что функция исчерпания многообразия М достигает минимума в М , который для определенности будем считать равным нулю.
Исходным примером функции исчерпания для нас является в случае полного многообразия М функция расстояния г = г(р), р Е М , текущей точки р до некоторой фиксированной точки р 0 Е М . Функция г порождает шаровое исчерпание многообразия геодезическими шарами B T (t), t Е (0, + то ), с центром в р 0 . Известно, что г — липшицева в М функция и |V г | = 1 почти всюду в М .
Далее, если функция h локально липшицева в М, то для произвольного ее значе ния t положим
S F, PAt) : = /
J E h (t)
F р (х, V h)/ |V h | ds,
где ds — элемент (п — 1)-мерной меры Хаусдорфа на М п (в метрике многообразия М п ). Величину S F,p,h (t) будем называть (F,p, h) -площадью h-сферы E h (t).
В классическом случае F(х, ^) = | ^ | для рассматриваемой в качестве функции исчерпания полного многообразия М функции расстояния h = г величина S p,h (t) (для любого р) совпадает с обычной площадью геодезической сферы S (t) радиуса t.
В свою очередь, роль обычного п-мерного объема V(U ) какого-либо множества U С Мп для произвольно заданной на нем локально липшицевой функции h будет играть следующая величина:
V F,p,h
(U ) := У F р (х, V h)
dv,
которую назовем (F,p, h) -объемом множества U .
Далее в качестве U рассматривается h-шар B ^ (t) и вместо обозначения V F,p,^ (B ^ (t)) используется символ V F,p,^ (t).
2.2. Критерии (F,p)-емкостного типа многообразия
В целях краткости формулировок будем говорить про некоторое свойство, что оно реализуемо в классе каких-либо объектов, если существует такой объект этого класса, для которого данное свойство имеет место.
Теорема 2. Некомпактное многообразие Мп имеет (F,p) -параболический тип тогда и только тогда, когда в классе его функций исчерпания реализуемо любое (или хотя бы одно) из следующих условий:
0) V^ p,^ и ) < го ;
VF,p,h ( t )
1) lim —,pp < го t^+^ t
+ ^
∑︁ i=1 x
( t i+1 — t i ) P
V F',p^ ( t i+1 ) — V F,p,h ( t i )
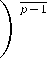
= го
для некоторой положительной возрастающей неограниченной сверху числовой последовательности { t i } , г E N , значений функции h ;
+ ro 1
/(ет) ”dt = ro , t0 > 0
t 0
-
4) ^ / tl+1 ( v . t - t' ) P —1 dt = ro
г=1 Jti \VF,p,h(t) — VF,p,h(ti U для некоторой положительной возрастающей неограниченной сверху числовой последовательности {t^}, i E N, значений функции h;
+ ^ i
-
5) / - 1 dt = 00 , t o > 0 .
J \bF,P,hVt); t o
Эти условия располагаются в следующем порядке подчиненности:
-
0) ^ 1) ^ 3) ^ 4) ^ 5) (4)
для любой, но одной и той же функции исчерпания h .
Отметим, что в основе получения приведенных емкостных критериев лежит ключевой критерий 0), который в классическом случае (то есть когда F(ж, ^) = | ^ | , р = п) восходит к следующему геометрическому критерию конформно параболического типа многообразия, первоначально, по-видимому, полученному В.А. Зоричем в обзоре [12] и, независимо в том же году, в статье [11].
Некомпактное риманово многообразие имеет конформно параболический тип тогда и только тогда, когда конформной заменой метрики его можно превратить в полное многообразие конечного объема .
Замечание 2. Согласно теореме 2, приведенные в ней условия 0)–5) эквивалентны между собой в классе всех функций исчерпания многообразия (F,p)-параболического типа. Однако, как утверждается в теореме 4, для одной и той же функции этого класса никакие из указанных условий уже не являются эквивалентными. Тем не менее каждое из приведенных условий 1)–5) является точным (в определенном смысле) достаточным условием (F, р)-параболичности типа.
Например, в условии 1) знаменатель t p нельзя, вообще говоря, заменить на функцию большего роста. Однако при некоторых дополнительных предположениях о функции исчерпания h ограничение на рост величины V F,P,h (t) (при t ^ + го ) в этом условии можно ослабить. Например, приведенный в теореме 2 список условий можно дополнить следующим (также точным) условием (F, р)-параболичности типа некомпактного многообразия М п .
Следствие 2. Предположим, что для некоторой функции исчерпания многообразия 1
М п функция S F -p h (t) является выпуклой вниз при всех достаточно больших t и выполняется условие:
1)’ lim < го .
/ > ■ ^ tp(ln t)p-1 .
3. Описание функций обобщенного объема в классе функций исчерпания многообразия
Тогда многообразие М п имеет (F,p) -параболический тип.
В работе Р. Гримальди и П. Пансу [11] было получено описание функций, которые могут служить на некомпактном полном многообразии М конформно параболического или конформно гиперболического типов функциями объема геодезического шара V(г) радиуса г для достаточно большого г при конформных заменах исходной метрики многообразия.
Мы приведем версию указанного результата для функций (F,p, К) -объема К-шара V h (t) на многообразии (F, p)-параболического или (F,p) -гиперболического типов, в которой роль конформно эквивалентных замен исходной метрики полного многообразия М будут играть функции исчерпания К данного многообразия.
Аналогично упомянутому результату работы [11], следующая теорема отвечает на вопрос, когда положительная возрастающая функция v(t), t Е [t o , + № ) (где t o > 0), реализуется как функция V FjPjh (t) при t > t 0 в классе функций К исчерпания многообразия М п , точнее, когда имеет место представление
V t > t o : v(t) = V F^h (t)
для некоторой функции исчерпания К многообразия М ?
Теорема 3. Предположим, что допустимая для (F,p) -емкости функция F (ж, ^) однородна по переменной ξ .
Пусть v = v(t) , t Е [t 0 , + то ) , — произвольная положительная возрастающая абсолютно непрерывная функция такая, что величина 1/v' локально ограничена.
Если многообразие М п имеет (F,p) -параболический тип, то функция v реализуется как функция V Fph (t) при t > t 0 в классе функций К исчерпания многообразия.
В случае если многообразие М п имеет (F,p) -гиперболический тип, то функция v реализуется как функция VF p^ (t) при t > t 0 в классе функций К исчерпания многообразия М п тогда и только тогда, когда она удовлетворяет условию
+ ^ 1
/ (^ У- 1 dt < № .
v ‘ (t)J
Используя теорему 3, можно обосновать высказанное выше в замечании 2 утверждение о том, что ни одна из импликаций, указанных в (4), вообще говоря, не обратима на произвольном некомпактном многообразии (F,p)-параболического типа (на многообразии (F,р)-гиперболического типа такой вопрос не возникает, поскольку, в силу теоремы 2, ни одна из этих импликаций в этом случае неверна).
Теорема 4. Предположим, что многообразие М п имеет (F,p) -параболический тип. Тогда в классе его функций исчерпания реализуема любая из следующих пар условий:
-
1) \ 0); 2) \ 1); 3) \ 1); 2) \ 3);
-
3) \ 2); 4) \ 2); 4) \ 3); 5) \ 4).
Здесь мы используем обозначение вида Л) \ В) для любой пары условий Л) и В' ) из теоремы 2 , которое означает, что для одной и той же функции исчерпания К условие Л) выполнено, а условие В ) не выполнено.
Следствие 3. Условие 1)’ следствия 2 вместе с предположением о выпуклости вниз 1
функции S F - p'h ( t' ) реализуемо в классе функций исчерпания произвольного многообразия (F,p) -параболического типа, так что утверждение следствия 2 является критерием (F,p) -параболичности многообразия в указанном классе.
При этом условие 1)’ находится в следующем порядке подчиненности с условиями 1) и 2) теоремы 2:
1) ^ 1) ’ ^ 2), (5)
а иные импликации между условиями теоремы 2, включающие условие 1)’, вообще говоря, не справедливы (для одной и той же функции исчерпания h при указанном 1
предположении выпуклости функции S p — h (t~)).
Кроме того, при ослаблении предположения в следствии 2 о выпуклости вниз 1
функции S- p -l h (t) , например, до предположения о ее монотонном возрастании, выполнение условия 1)’, вообще говоря, не гарантирует (F,р) -параболический тип многообразия М п .
4. Достаточные условия параболичности через «взвешенные объемы» шаров
Как уже отмечалось выше, на полном многообразии М п в качестве его функции исчерпания h традиционно выступает функция расстояния г = г(х), х Е М п , до некоторой фиксированной точки х 0 Е М п . Напомним, что |V r | = 1 почти всюду в М п . Поэтому в классическом случае F(х, ^) = | ^ | величины V p,p,h (t) и S pp,h (t) представляют собой, соответственно, п-мерный объем V(t) и (п — 1)-мерную площадь S(t) сферы геодезического шара B(t) радиуса t (с центром в точке х 0 ).
Тогда приведенные в теореме 2 условия 1)–5) представляют собой достаточные условия р-параболического типа некомпактного полного многообразия М п в терминах роста величин V (t) и S(t) при t ^ + ^ .
Эти достаточные условия р-параболичности, вообще говоря, хорошо известны и, по-видимому, впервые были получены в следующем порядке: условие 1) при р = 2 — C. Ченгом и C. Яу в [8], а при произвольном р > 1 — в [3]; условие 2) — в [10], условие 3) — А. Григорьяном (при р = 2) в [1], а для произвольных р > 1 — в [2]; условие 5) — Л. Альфорсом (при п = р = 2, причем как критерий параболичности поверхности в классе ее конформных изоморфизмов) в [7]. Для общего вида функции F(х, ^), но однородной по ^, условие 5), как достаточное условие (F,р)-параболического типа, непосредственно вытекает из оценки (F,р)-емкости, установленной в [5].
На самом деле, из теоремы 2 можно получать за счет выбора отличной от г функции исчерпания h и другого вида достаточные условия (F,р)-параболического типа многообразия. Приведем один вид таких условий р-параболичности, в которых вместо объема шаров используется их «взвешенный объем».
Предварительно для произвольного множества U С М и любой заданной на нем липшицевой положительной функции h введем, следуя В.М. Миклюкову, величину
v
(U) := / и
h q dv,
q E R ,
которую назовем h -взвешенным объемом множества U .
В частности, в качестве h можно взять ту же функцию г расстояния на М (до некоторой точки х 0 / U ). В простейшем случае q = 0 «взвешенный объем» V h [0] (U) представляет собой обычный п-мерный лебегов объем множества U .
Следствие 4. Пусть h — какая-либо липшицева функция исчерпания на некомпактном многообразии М п .
Предположим, что выполняется одно из следующих условий:
1а) lim Vi:^)) < +то tF+ю tp-:
для произвольного числа q такого, что q < р ;
"- г(
t ^p-W
v^Wt))
)
i/(p-i)
dt
-^ = то t p/p
для произвольного числа q такого, что q < р ;
2а) lim t:-p V^(Mп \ Bh(t) < +то для произвольного числа q такого, что q > р;
/ + ^
i/(i - p) dt
= то t :/p
(t(4-p^/pv£J4Mп \Bh(t))j для произвольного числа q такого, что q > р;
v V [ p ] (Bh (t))
3а )
l^m " , p, ” < + то ;
. . x ln p t
3b) / ()
V )Jpl (B , (t))
1/(p - 1)
dt
— = то t
(условия 2a) и 2b) имеют смысл, конечно, только, если V^^(M п ) < то ).
Тогда многообразие М п имеет р -параболический тип.
Условия 1a), 2a), 3a) на рост «взвешенного объема» впервые получены В.М. Ми-клюковым (см. по этому поводу [6]; условие 3 a) использовалось также в [4]). Отметим, что соответствующие им условия 1b), 2b), 3b) допускают несколько более высокий рост «взвешенного объема».
Например, р-параболичность типа многообразия на основании условия 1b) будет обеспечена, если (ср. с условием 1a))
— V [ q] (B h (t))
lim < +то , q < р, t^+^ tp-pF (t)
где F = F(t ), t > t o > 0, — произвольная положительная функция, для которой
Г+^ dt _
J t(F (О) 1/»'-1) = то •
В частности, в качестве F могут выступать функции вида F (t) = (ln t) p 1 , F (t) = = (In t Inln I/) ’ 1 и т. п.
Список литературы Понятие и критерии емкостного типа некомпактного риманова многообразия на основе обобщенной емкости
- Григорьян, А. А. Об одной лиувиллевой теореме на римановом многообразии / А. А. Григорьян // Успехи матем. наук. - 1982. - Т. 37, № 3. - C. 181-182.
- Зорич, В. А. О конформном типе риманова многообразия / В. А. Зорич, В. М. Кесельман // Функциональный анализ и его приложения. - 1996. - Т. 30, № 2. - C. 40-55.
- Кесельман, В. М. О римановых многообразиях a-параболического типа / В. М. Кесельман // Изв. вузов. Математика. - 1985. - № 4. - C. 81-83.
- Кесельман, В. М. О поведении «в целом» неограниченных гиперповерхностей с квазиконформным гауссовым отображением / В. М. Кесельман, В. М. Миклюков // Сиб. матем. журн. - 1984. - Т. 25, № 6. - C. 195.
- Мазья, В. И. Пространства С.Л. Соболева / В. И. Мазья. - Л.: Изд-во ЛГУ, 1985. - 416 c.
- Миклюков, В. М. Геометрический анализ / В. М. Миклюков. - Волгоград: Изд-во ВолГУ, 2007. - 530 c.
- Ahlfors, L. Sur le type d'une surface de Eiemann / L. Ahlfors // C.R. Acad. Sci. Paris. Ser. A. - 1935. - Vol. 201. - P. 30-32.
- Cheng, S. Y. Differential equations on Riemannian manifolds and their geometric application / S. Y. Cheng, S.-T. Yau // Comm. Pure and Appl. Math. - 1975. - Vol. 28. - P. 333-354.
- Choquet, G. Theory of capacities / G. Choquet // Annales de l'institut Fourier. - 1954. - Vol. 5. - P. 131-295.
- Coulhon, Th. Harnack inequality and hyperbolicity for subelliptic p-Laplacians with applications to Picard type theorems / Th. Coulhon, I. Holopainen, L. Saloff-Coste // Geometric and Functional Analysis. - 2001. - Vol. 11, № 6. - P. 1139-1191.
- Grimaldi, R. Sur la croissance du volume dans une classe conforme / R. Grimaldi, P. Pansu // Math. pures et appl. - 1992. - Vol. 71. - P. 1-19.
- Zorich, V. A. The global homeomorphism theorem for space quasiconformal mappings, its development and related open problems / V. A. Zorich // Lecture Notes in Math. - 1992. - Vol. 1508. - P. 131-148.


