Поперечные электрические флуктуации в квазидвумерной сверхрешетке с "параболическим" законом дисперсии

Частное решение уравнения (4) ищем в виде

g(Рх’Ру) = (^яМ"п\ 5(py)e"pJcL'r

А_хв( РхЖ^Г- Л | +

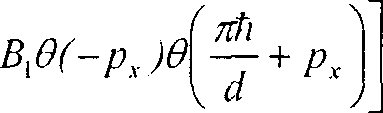
где 6(х)- ступенчатая функция Хевисайда. Подставляя (5) в (4), находим уравнения для определения постоянных Д, и В. ₃

- Ave^,,cE-dr + Bie*icE-lk =0

Аналогично записываются условия для А, и В, (с заменой в (6) Е_х —> E_v ). Из (6)

находим

При E_v =0 полученное решение ((5),(7)) переходит в функцию распределения, найденную в [6] применительно к одномерной СР (ОХ - ось СР). То же самое имеет место и в случае Е_х = 0, когда OY - ось СР.Таким образом, функция распределения (5), состоящая из двух независимых слагаемых, относится к ситуации, когда оси ОХ и OY направлены вдоль главных осей простой квадратной решетки.

Как нетрудно видеть, уравнение (4) ковариантно относительно поворотов системы координат, и поэтому для любой другой («штрихованной») системы в уравнении (4), а значит, и в решении (5) достаточно сделать замены р -> р', Ё -> Ё' ■ Далее считаем «штрихованной» рассмотренную выше систему координат.

В интересующем нас случае, когда оси координат повернуты на 45° относительно главных осей квадратной 2СР, имеем

Рх⁺Рг Pv-Px E_x+E_v _ E_v-E_x

= р'-"- < е-‘— '      <8)

Подставляя (8) в «штрихованную» функцию (5), находим соответствующую данному случаю функцию распределения, с помощью которой вычисляем плотность тока

е

(2лй )"

J f A^-g(Px,Pv)^dPxdp_y

В результате имеем

1л     л

(Ю)

2\Jh^(E~+Ej)+ sh^/(Ev-Ej) J ’ где единицей измерения напряженности поля является величина Ео = Т2Й / edr , а плотности тока - у0 = 2пеМ/лгЬ . Выражение для js записывается аналогично (10) с заменой х<^у.

Пусть в направлении OY образец гальванически разомкнут:

Л=0.                                 (11)

Подставляя (10) в (11), получаем уравнение для спонтанного поперечного поля E_v, решения которого имеют вид

ФИЗИКА

о,

Отметим, что точка бифуркации Е _с = 1.174 в точности совпадает с положением максимума функции (10) при Е_х =0.

Устойчивость полученных решений определяется неравенством dEv дЕ;

где Ф = ^j_vdE_v+const - синергетический потенциал. Условия (11) и (13) выполняются при £, = Е„ , а значит, решения (12) соответствуют минимумам потенциала Ф. Таким образом, как и в случае косинусоидального закона дисперсии [1 -4], здесь мы имеем дело с НФП второго рода.

Справа от точки бифуркации потенциал имеет вид Ф^Е;,Е^=^Е(Е_Х+Е_у)+Е(Е_Х-Е_?.)) , (14)

где

Е(х) = ^---В₀х² + лВ_г //7|х|^- +

у (1-1^2к )в_1к р?*'² ^(2к-2)(2к)! UJ

(H>D.

Здесь 5„ - числа Бернулли.

На рис. 1 представлен синергетический потенциал Ф для различных значений тяну щего поля.

При учете флуктуаций тока ^8jv(t)^ условие разомкнутости по полному току в OY- направлении принимает вид

dE_v 4я ЭФ

dt

е дЕ

4д .

--5k(t) 8           ’

где е - диэлектрическая проницаемость. Токовая корреляционная функция для теплового (аддитивного и некоррелированного) шума равна [7]

^jv(t)5jv(t ^ = ^^8(1-1 ), (17) где V - объем системы, а ст - электропроводность в слабых полях. В данной работе мы не учитываем влияния электрического поля на коррелятор (17). При этом стоит заметить, что учет этого влияния приводит лишь к непринципиальным поправкам в окончательных результатах в аналогичной задаче для косинусоидального закона дисперсии [8].

Далее, переходя от уравнения Ланжевена (16) к эквивалентному ему уравнению Фоккера - Планка для функции распределения w=w(E;,E²,t) случайной величины E_v [9]

8 dw д . .   .    ._ d'w

--— —— (j лм) + ш(Т ) —— 4л dt dEv '          дЕ;

где у(Т) = 4локТ1еУ , находим стационарную функцию распределения

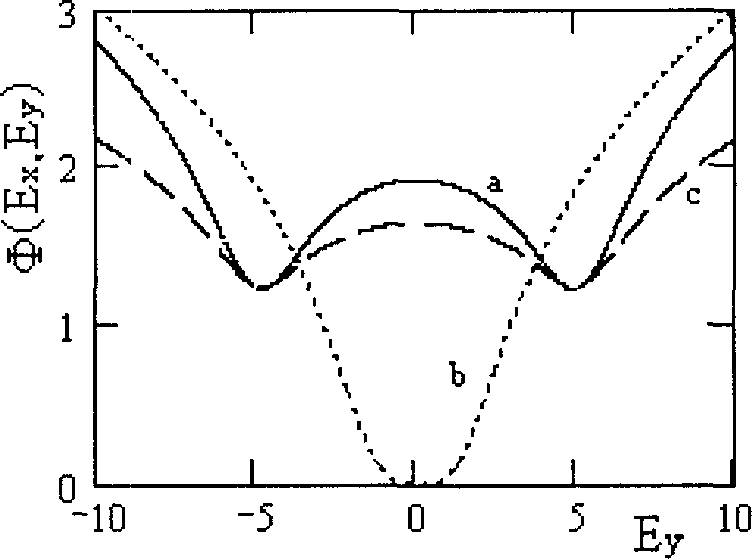
Рис Л. Синергетический потенциал как функция поперечного поля Е для различных значений поля Е_х: а - Е_х=3; b --Е_х=1.174; с - синергетический потенциал для косинусоидального закона дисперсии (Е_х=3)

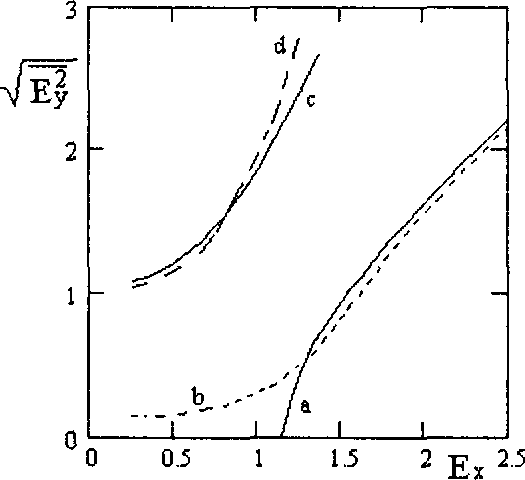
Рис.2. Поперечное электрическое поле как функция тянущего поля: а - E_v- E_vs ; b - поле ^Е^, рассчитанное по формуле (20) при а = 50 ; с и d - отношение поля -^Е^к значению поля Найквиста (1/VcT) для а = 10 и а = 20 соответственно

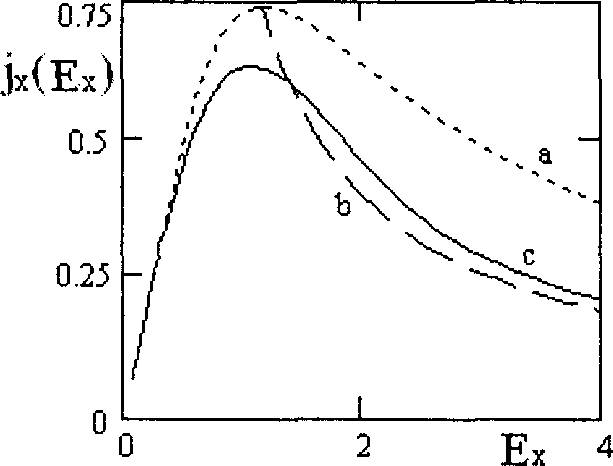
Рис.З. Вольт-амперная характеристика

при различных значениях поперечного поля: а — Е_¥ = 0; b - E"_v = Е'„; с - Е_у = Е_у

w(E;,E_¥) = Ae"“*,                                    (19)

где А = А(Е_х,а) — нормировочная постоянная, a = sV]4nkT.

Средний квадрат флуктуаций поперечного поля находится по формуле

Е\.(Е;,а) =

^E;w(E;,E;,a)dE¥ ^w( E;,E;,a)dEv _

Примеры поведения ^Е_¥ представлены на рис.2.

При отсутствии тянущего поля (Е_¥ =0) и при а » 1 из (20) с учетом (14) имеем £² «\(а , что практически совпадает со стандартной формулой Найквиста [7] ( Е;. = \/а);

это означает, что предлагаемая теория справедлива при а »1 •

Спонтанное поперечное поле влияет на вид вольт-амперной характеристики сверхрешетки. Подставляя квадрат поперечного поля в выражение для jx, находим зависимости jx—jx(Ex) в различных случаях.

Численные оценки результатов сводятся в основном к оценке величины Ес. При d=10'7 см, т =10"12 с величина Ес=900 В/см.

ЛРх.Ру) = -;- г f \g(Px- Рх.Ру- Py)f₀(Px,Py)^dPxdp_y . (21)

Знание температурной зависимости f необходимо, например, для исследования стохастического резонанса в 2СР. Соответствующие результаты будут представлены в отдельной публикации.