Построение гидрогеохимических разрезов с учётом структурно-литологического строения отложений

В настоящее время значительным препятствием для содержательного анализа гидрогеологических и, в частности, гидрогеохимических данных являются проблемы с построением детальных пространственных моделей изучаемых показателей. Традиционно используемые карты для отдельных горизонтов или комплексов не отражают в полной мере сложную картину изменения параметров по разрезу отложений. Задача анализа и прямого картирования данных по разрезу наследует множество проблемных вопросов, связан- ных с фрагментарностью данных и их невысокой достоверностью. И в значительной степени эта задача усложняется необходимостью учета структурнолитологического строения отложений, их анизотропии, поскольку этот фактор оказывает решающее влияние на неравнозначность субвертикального и сублатерального направлений при прослеживании содержания как отдельных водорастворенных компонентов, так и общей минерализации подземных вод.

Для учёта особенностей строения отложений при картировании в этих условиях необходима разработка специальных методов и их апробация в решении практических задач. Среди множества методов решения этой задачи наиболее подходящим и эффективным для построения карт в анизотропных средах, на наш взгляд, является вариационный метод геокартирования, который позволяет реализовывать разнообразные условия средствами физико-математического моделирования [1, 2, 4, 7].

Для применения различных модельных представлений и для учета информации о свойствах картируемого показателя в точках наблюдения в этом методе заложены возможности добавления в минимизируемый функционал условий приближенной согласованности достаточно общего вида глобальных уравнений (характеризующих модельные условия) и локальных уравнений (представляющих результаты и условия наблюдений в точках).

В этом методе обеспечивается возможность использования не только значений картируемого показателя в точках наблюдения, но и значения первых и вторых производных. Например, для согласования результатов сейсмических исследований могут использоваться значения, зафиксированные в отдельных пикетах, а также величины изменения параметра в направлении между пикетами (производные по направлению). При картировании напора подземных вод условия непротекания могут задаваться непосредственно в виде локальных уравнений в частных производных, определяющих равенство нулю производной напора по направлению вектора нормали к границе. Условие постоянства напора (значение которого неизвестно) вдоль некоторой линии (например, зоны разгрузки) может задаваться аналогично, только условия в этом случае имеют вид равенства нулю производной вдоль линии границы.

Этот же подход может использоваться для учета косвенной информации, задаваемой в виде некоторых границ, геометрию которых необходимо учитывать при решении задач геокартирования. Например, при построении гидрогеохимических карт (минерализации и содержания основных водорастворенных компонентов) водоносных комплексов Западной Сибири предположение о наличии контроля химического состава подземных вод литологическими свойствами вмещающих пород учитывалось введением условия приближенного постоянства вдоль границ выделяемых стратонов картируемого показателя (равенства нулю его производной) [6].

Аналогичный подход даёт относительно неплохие результаты и при построении гидрогеохимических разрезов, например, с применением условий выдер- жанности гидрогеохимических параметров вдоль границ залегания основных флюидоупоров – кровли кристаллического фундамента, юрского, неокомского и апт-альб-сеноманского водоносных комплексов. Но отрицательным моментом является то, что с удалением от границ водоносных комплексов их влияние уменьшается и согласованность геометрии изолиний минерализации и границ комплексов, соответственно, уменьшается. Очевидно, что при наличии более детальной информации о структурно-литологическом строении разреза в рамках такого подхода можно обеспечить необходимое согласование с имеющимися данными о минерализации подземных вод. Однако такая детальность информации не всегда доступна или усилия по ее подготовке и преобразованию в требуемый вид не всегда приемлемы по отношению к уровню значимости получаемых результатов для решения конечных практических задач.

Определенным недостатком рассмотренного выше варианта учета пространственной анизотропии является также то, что в качестве модельных условий рассматривается только ее латеральная составляющая, а вертикальная определяется исходя из иных физических предпосылок. На наш взгляд это снижает общность постановки задачи по учету анизотропии и тем самым уменьшает возможности по обеспечению надежных результатов построений в условиях широкого разнообразия свойств геологических объектов и характера их пространственной неоднородности.

Необходимые для таких задач черты общности обеспечивает подход к моделированию анизотропии на основе аналогии с результатами воздействия деформационных процессов на изначально недеформи-рованный геологический объект. В рамках используемого нами вариационного метода геокартирования, реализующего средства физико-математического моделирования, постановка и решение задачи учета деформационного преобразования (при условии его однозначности и гладкости до второго порядка включительно) осуществляется достаточно просто.

% (u, v), у (u, v), u(x, y), v(x, y) (1) решение преобразуется к виду

S*(u, v) = S*(x(u, v),y(u, v))

Это решение может быть получено и другим путем. Соотношения между координатами (1) можно использовать для соответствующего преобразования вида дифференциальных операторов локальных и глобальных уравнений, и решать задачу минимизации функционала непосредственно в координатах преобра- зованного пространства.

Изменение дифференциальных операторов первого и второго порядка локальных и глобальных урав- нений при переходе к новым координатам осуществля- ется в соответствие с известными правилами диффе- ренцирования сложных функций

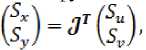
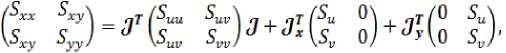
где 3(u,v) – матрица Якоби преобразования

3 =

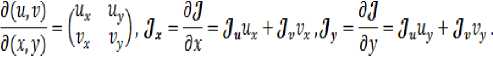
Условием невырождённости преобразования является отличие от нуля определителя матрицы Якоби (UI * 0). Интегралы, входящих слагаемыми в минимизируемый функционал, преобразуются согласно соотношениям

J F(x,y)dxdy = J F(x(u,v),y(u,v))|J|-1dudv.

a n' (4)

Таким образом, соотношения (2 – 4) позволяют переопределить используемые в задаче картирования исходные данные в точках наблюдения и модельные условия в форму соответствующих дифференциальных уравнений в частных производных, учитывающих локальные особенности деформационного преобразования в каждой точке области картирования. Представляется очень важным, что для реализации такого решения не требуется непосредственного использования функция преобразования координат (1). Достаточно только информации о матрице Якоби такого преобразования.

Отметим, что в рамках численной схемы реализации вариационно-сеточного метода в общем случае невозможно строго учесть преобразование области интегрирования 11 в область Q и, соответственно, получаемое решение является приближенным. Однако, учитывая аппроксимационный характер самого вариационного метода картирования, а также то, что использование деформационной модели в этом подходе реализуется не на базе строгого описания физических процессов, а лишь в качестве ассоциативной основы, обеспечивающей ожидаемые результаты картирования в условиях анизотропии, такое приближение представляется допустимым.

Входящая в соотношения (2 – 4) матрица Якоби играет очень важную роль и вместе с тем имеет достаточно простую физическую интерпретацию. Ее можно представить как результат последовательного воздействия трех простых преобразований – поворота, сжатия и скоса. Матрицы Якоби этих преобразований с точностью до масштабного множителя могут быть представлены в виде:

= /cos(a) sin(a)\ = /1 0\ /1 tg^X \-sin(a) cos(tz)/,j2 \0 уН3 ^0 1 '

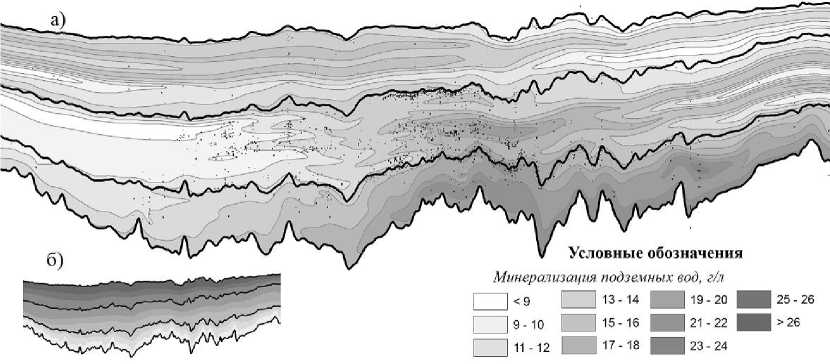
Рис. 1. Картирование минерализации подземных вод по разрезу отложений (а - с учетом анизотропии, б - модель строения отложений).

для преобразования поворота на угол --"' ■ масштабного изменения (растяжения или сжатия) по одной из осей в ■' раз, для преобразования скоса на угол ^ . соответственно. Матрица Якоби результирующего преобразования определяется произведением (в необходимом порядке) матриц 3-_, 3- и 3, .

Очевидно, что вследствие различий в природе самих картируемых показателей, причин, определяющих анизотропию их изменения в пространстве, а также условности самого подхода по моделированию деформационного преобразования в рассматриваемых здесь задачах геокартирования, не существует единого алгоритма для определения коэффициентов матрицы Якоби. Однако ясный физический смысл параметров л. 5 ну позволяет использовать их как показатели анизотропии, которые могут быть относительно просто определены на основе имеющейся геологической информации о свойствах геологических объектов (например, о геометрии залегания пластов).

Отметим, что параметры л. 5 ; I у могут быть как постоянными, так и переменными в области картирования, что позволяет единообразно осуществлять расчеты для вариантов, как с однородной, так и с неоднородной анизотропией.

Определённые сложности в реализации рассматриваемого подхода связаны с необходимостью обоснования выбора модельных закономерностей (в виде глобальных уравнений), определяющих изменение свойств геологических объектов в некотором абстрактном исходном, недеформированном пространстве. Это обусловлено неоднозначностью и значительной долей условности самой постановки задачи учета анизотропии на основе моделирования деформационного преобразования.

Однако как показывает практика решения задач геокартирования (без учета анизотропии) в большинстве случаев вполне приемлемые результаты обеспечиваются применением стандартных условий минимума кривизны и (или) минимума поверхности. При этом для свойств, изменения которых ограничены в достаточно узких пределах (например, пористость пород), или не имеющих явных трендовых изменений в про- странстве, предпочтительно использовать условие минимума поверхности. А для свойств, в изменении которых могут быть значительные трендовые изменения (например, при построении структурных планов), надежнее использовать условие минимума кривизны. В задачах картирования с учетом анизотропии, очевидно, можно также применять оба этих стандартных подхода, по крайней мере, в качестве первого варианта решения.

Рассмотрим пример использования этого подхода для учета структурно-литологического строения отложений при картировании гидрогеохимических разрезов. В качестве исходных данных для этого примера взяты результаты определения общей минерализации подземных вод глубоких горизонтов Западно - Сибирского нефтегазоносного бассейна в области субширотного направления от Красноленинского района на западе, до Пыль-Караминского на востоке, протяженностью около 1000 км и шириной 50 км. На рис. 1а приведены результаты выполненного картирования с использованием преобразованного условия «минимума поверхности». Местоположение данных со значениями минерализации подземных вод по разрезу отложений на рисунке представлены точками черного цвета.

Для учета анизотропии при построении учитывалась геометрия залегания кровли (и подошвы) основных водоносных комплексов (апт-альб-сеноманского, неокомского, юрского и палеозойского) и закладывалась модель унаследованного осадконакопления, при которой в залегании отдельных пластов прослеживаются черты структурных планов нижележащих и вышележащих отложений. Модельная схема строения отложений, использованная для построения, представлена в виде отдельной вставки (рис. 1б).

Матрица Якоби в данном примере определялась как результат преобразований поворота и сжатия, т. е. в виде произведения двух матриц 3 ■_ и 3:. Коэффициент । принимался постоянным, угол ■"•: определялся в каждой точке картирования в соответствии с углом залегания пластов (в рамках используемой модели строения отложений). Отметим, что величина параметра , может быть различной и определяться, например, исходя из данных о палеогеографических условиях формирования разреза осадочного чехла, которые для юрско-меловых отложений Западной Сибири к настоящему времени достаточно детально изучены.

Как видно из рисунка, полученная картина распределения минерализации подземных вод по разрезу отложений вполне соответствует ожидаемому виду рассматриваемой анизотропии – выдержанности значений по напластованию отложений и существенно большей вариативности в поперечном направлении.

Отметим, что приведённый пример выполнен в рамках существующего программного комплекса GST [3, 5]. В этом же комплексе выполнены сопутствующие построения, в частности построение схемы строения отложений на основе модели унаследованного осадконакопления. При необходимости, возможности комплекса позволяют реализовывать и другие, более сложные варианты учета анизотропии. Заложенные в GST средства алгоритмизации геоинформационных технологий обеспечивают возможность выполнения (при необходимости в автоматизированном режиме) последовательного построения всех необходимых промежуточных данных и конечного результата в рамках единого проекта. Также могут использоваться реализованные в GST специализированные средства, такие как учет разнообразной косвенной информации, оценка достоверности выполненных построений, картирование с учетом интегральных условий и другие.

Подход к моделированию деформации на основе преобразования дифференциальных уравнений в частных производных, определяющих модельные условия при решении задачи картирования, очевидным образом обобщается на случай трехмерных задач. Этим снимаются значительные трудности постановки и решения содержательных задач трехмерного моделирования, в которых неоднородность и анизотропия отложений, как правило, является неотъемлемым и важнейшим внешним фактором, определяющих закономерности пространственного изменения свойств геологических объектов.

Работа выполнена при поддержке гранта РФФИ № 15-05-01982 А.