Построение компромиссного набора стратегий в одной линейной дифференциальной игре трех лиц

В работе [4] автором был предложен один способ рационального поведения игроков, названный им принципом компромисса, для конфликтной ситуации, в которой интерес каждого игрока, помимо минимизации своей платы, состоит еще и в том, чтобы любой из его оппонентов не мог получить результат лучший (меньший) некоторой заданной величины. Предложенный подход состоял в том, что компромиссный набор стратегий игроков обеспечивает каждому игроку значение платы не хуже (не больше) верхней компромиссной оценки. При этом никакое единоличное уклонение игрока от стратегии, предписываемой компромиссным набором, не позволяет ему получить значение платы лучше (меньше) нижней компромиссной оценки.

Реализация указанного набора стратегий осуществлялась путем построения системы гладких потенциалов, представляющих собой непрерывно дифференцируемые функции текущего времени и фазовых координат, производные которых в силу дифференциальных уравнений движения сохраняют постоянный знак. Формализация стратегий игроков и отвечающих им движений соответствовала

подходу, принятому в монографиях Н.Н. Красовского и А.И. Субботина [1–2] для антагонистических дифференциальных игр и обобщенному на случай игр нескольких лиц А.Ф. Клейменовым в работе [3].

В статье был также рассмотрен пример, иллюстрирующий развиваемую теорию. На взгляд автора приведенный пример не в полной мере использовал возможности изложенного алгоритма, так как динамика игры в этом примере представляла собой лишь "простое движение".

Настоящая работа посвящена построению и исследованию модельного примера, адекватно отражающего возможности алгоритма реализации принципа компромисса на базе построения системы гладких потенциалов.

1. Описание игры

Динамика игры описывается линейным векторным дифференциальным уравнением вида

^ X

к ^х з 7

к 2

1 7 к x 7

^ U 1

(w

^{+ u 2}

к u 3 7

к v 7

+ w 2

к w 3 7

(1.1)

Игра заканчивается в момент времени T . Це-

левыми множествами служат точки в трехмерном пространстве (рис. 1):

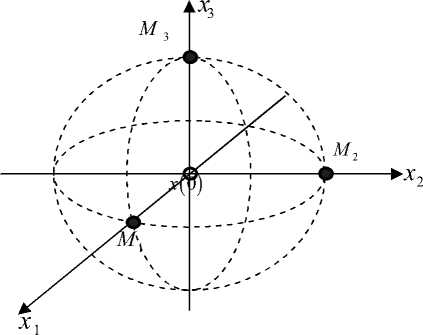
Рис. 1

Коши однородной системы

Г x 1 3		Г 1	4	1 3	Г x 1 3
x 2	=	1	1	1	x 2	(2.1)
к x 3 7		к 2	- 4	1 7	к x 3 7

имеют вид x11 [ t ,т] = 5 e3( ‘т) + у cos (t - т )-- Isin (t- т), x12 [t,т] = Ie3(tт) -1cos(t-т) + +y-sin (t - т),

M i =

Г m\ m ?

( i ) m () к ³ 7

i = 1,2,3,

где ml1 =1, m21 = 0, m^1 = 0, m(2) = 0, m22) = 1, m32) = 0, m(3) = 0, m 23) = 0, m 33) = 1.

На рис. 1 показано расположение целевых множеств игроков. Геометрическим ограничением на управления является множество

г u? u 2	’	Г v v 2	’	г w 1 3 w	e P =
к u 3 7		к v 3 7		4 w 3 7

= 1 P 2

p 1 ⁺ p 2 ⁺ p 3 ^ ¹ ’ .

^ P 3 7

Заданы нижние компромиссные оценки

S, = 0.8, S ₂, = 0.8, S ₃, = 0.8 1 *                2 *                3 *

и верхние компромиссные оценки

S 1 * = 0.9, S 2 * = 0.9, S ₃ * = 0.9.

• ^- |srn ( t ^{- т} ),

x 2i [ t , т ] = -5 e ^{3 (} t ^-т ) -1 cos ( t - т ) -

• ^- } Sin ( t ^{- т} ) ,

x ₂₂ [ t , т ] = I e ³⁽ t ^{- т} ) + -5 cos ( t - т ) +

+f-sin (t - т), x23 [t,т] = 130e3(‘ ■') -130 cos (t - т) +

+^sin (t - т), x31 [ t ,т] = 2sin (t - т), x32 [t, т] = -4sin (t - т), x32 [ t, т] = cos (t - т) + sin (t - т),

Выпишем гладкие потенциалы, отвечающие нижним компромиссным оценкам

M t , ^x ) =

= max

max ll , X [ T , t ] x) - max ll , m) I II l = 1 L'       ^L ' m e m. '

\ ( t - 1 ) ,0 } =

2. Построение гладких потенциалов

Выпишем характеристическое уравнение для системы (1.1) и найдем его корни:

= max 1 max

II ^l ll=1

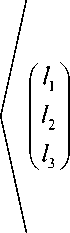
Г 3      .    . 3

X x1 j[ T, t ] xj j=1

X x 2j[ T. ' ] xj j=1

X x 3 j [ T ’ t ] x j к j = 1                7

1 - A 4     1 1    1 - A 1	= 0 ^
2     - 4  1 - A

3 - A + 3 A ² - Л³ = 0 ^ Л = 3, A 2, ₃ =± i .

Элементы фундаментальной матрицы

- max me Mi

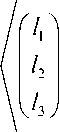
m

m

m

( ‘ )

2 i ’

3 j

,0

= max <  max

II l = 1

E is E x([ t , t ]

s = 1

к J = 1

^x J

j

^- E ^l s m i i s = 1

где

= max <

E l s ( z s ( t ^, x )^- m s ) ) s = 1

^z s ( t , x ) = E X sj [ T , t ] X j , s = 1,2,3 .

j = 1

Вектор l ⁰ ( t , t , x ) e { l e R³| ||l || = 1 } , на

6A

—s* t , x = 5 1

⁽4 ^d z s ⁽ t , x )

E(zs(t,x) ms)

=  /32

J E ( z s ( t , x ) - m s¹ ) )

V s = 1

d t s '⁽ t , x ) =

E (z( t, x)-m^-^x s =1                            d t

< / E( zs (t,x)-ms'))

V s = 1

- e i , i = 1,2,3 ,          (3.1)

котором достигается максимум, имеет вид l0 (t, x ) = f z1(t, x)- m.

=    3       ^{1             z} 2 ⁽ t , ^{x )- m} 2^

. E( z s ( t , x ) - m «) [ z з ( t , x ) - m 3^ V s = 1                                                     ^X

Тогда для всех i = 1,2,3 находим

ε t,x dX1 i, ) d

—S . ( t , x )

^d x ’ d

Ld x- ^s * ⁽ t , ^x )

j

S . ( t , x ) = max <

E ( z s ( t • x )^- m ?) +

+ a , ( T - 1 ) ,0 } .

Аналогично вычисляются гладкие потенциалы, отвечающие верхним компромиссным оценкам:

s * ( t , x ) = max { max [( l , X [ T , t ] x ^ -

- max ll , m} + e i m e M i '

= max <

E ( z s ( t • x )

- m s ’)’ + в , ( T - 1 ) ,0

3. Компромиссное управление

Для формирования неравенств, определяющих набор компромиссных управлений, требуется вычислить частные производные от потенциалов. Имеем

s*( t,x ) = dx та sx«

- T- s ( t , x ) ^d x ’

d

S ( t , ^x ) d x ₃

j

i E( zs(t, x)- ms)

\ s = 1

^x E ( z s ( t , x ) - m s ) ) ^x .

s = 1

x

a x

³ z s ⁽ ' , x ) a x ’

3zs (t,x > к   5x3   J

, i = 1,2,3.        ⁽3.²⁾

Выпишем левые части неравенств, определяющие компромиссные управления игроков в каждой текущей позиции ( t , x ) . В силу (3.1), (3.2) находим б

— s* t, x + б t 1Л ’

+ min u e P

—

]□ ( Z s ( t . x ) — m ! ")'^ s = 1                                  ^d t

i( zs (t ■ x)—ms1’)

s = 1

—

— a 1 + .               = x

J i( zs (t ■ x)—m()) V s =1

^x mn( i ( z s ( t ■ x ) ^— m s °’) ^-

\ s = 1

M t i x !

a x , MM a x 2 MM

V ^{d x} 3    7

,

' 1

( X i ^

' u 1 + v 1 + w1 ^л

x ₂

x +

u ₂ + v ₂ + w ₂

V ²

— 4

1)

x

X

d лх dt 82* ( t■ x) +

d

+ min —8 (t, x), Ax + u + v + w > = vEP \xx M 7

i( zs (t, x)

s = 1

—

m ( M& s jM ^s ) d t

Д z s ( t ■ x )^— m S ’) s = 1

— a 2 +

X

+          ^ X

л i( zs (t, x)—ms’)

i( zs (t, x)—mi2’)- s=1

i ( z s s = 1

( t , x ) —

V u 2 + v 2 + ^w 2 7 m . ^d z s ⁽ t , x ) ^s )       d t

i ( z s ( t ■ x ) ^— m s ^)

s = 1

—

a 1 +

+

=• X

i( zs (t, x)—ms >)

s = 1

i( zs (t, x)—ms1’)- s=1

'MM' a x .

MM a x 2

MM

V ^{d x} 3    7

—

,

^ x 1 + 4 x ₂ + x ₃ + v 1 + w 1 ^л

^x 1 + x 2 + x 3 + v 2 + w 2 _V 2 x 1 — 4 x ₂ + x ₃ + v ₃ + w 3

3       3,                            x

i i( zs (t, x)—ms1’)

s = 1

—

(^azst^x)

d x j

i( z s ( t , x ) ^— m s 9

s = 1

■ ( 3.3 )

^d z^{s (} t , ^x )' ■ x 1

dzs ( t, x )

^{d x 2}

^d z s ⁽ t , x ) Эх

V ^{d x} 3    7

,

' x 1 + 4 x ₂ + x 3 + u 1 + w 1

x 1 + x ₂ + x ₃ + u ₂ + w ₂

_V 2 x 1 — 4 x ₂ + x ₃ + u ₃ + w 3

i Z(z,(‘■ x)-ms!))

s = 1

—

,(2)\ ^d z s ⁽ t , x )

d x j

3 ₂ i ( z s ( t ■ x )^— mv}

. ( 3.4 )

—M t ■ ^x ) +

d

+ min( — s ₃ J t , x ), Ax + u + v + w) = ^{w e} P \ xx

i ( Z , ( t , x ) — m )' "t" s = 1                              ^d t

^(zs (t■ x) — ms ’)

s = 1

— a 3 +

+            = X

A i( Zs ( t, x) — ms’)

—

X

X ( z s ( t , x )^— m s ³⁾) ^ s = 1

^d z^{s (} t , ^x ) a x ^d z s ⁽ t , ^x ) a x 2

dx

V    ^d x 3    7

^x x 1 + 4 x ₂ + x 3 + u 1 + v 1

x + x 2 + x 3 + u 2 + v 2

_V 2 x 1 — 4 x ₂ + x ₃ + u 3 + v 3

X E(z.(t,x) — ms”)

s = 1

-

, (3Y\^dzsl^t,^x l

,

+ ,           =X

, X( zs ( t, x ) — mF)

^X( Д ( z s ( t , x ) - ^ s ¹’) ^ \ s = 1

f^ z s l ' T x ! 'I 0 x 1 ^d z s ⁽ t , x ) a x 2 ^d z s ⁽ t , ^x )

V    ⁵ x ₃    )

^л x 1 + 4 x ₂ + x ₃ + u 1 + v 1 + W 1 ^л

,

^d x j

X ( z s ( t , x ) - ^ s ^}) s = 1

. ( 3.5 )

x 1 + x ₂ + x ₃ + u ₂ + v ₂ + W _{2 V} 2 x 1 — 4 x ₂ + x ₃ + u ₃ + v ₃ + W 3

, ( 3.6 )

d./x/a./x,

— s ( t , x ) + ( — S ( t , x ) , Ax + u + v + w} = a t ^{2 (} , ) \a x ^{2 (} , )

d*/\/S*/4.

— S , ( t , x ) + ( — s , ( t , x ) , Ax + U + v + W = a t          \a x

X (z, (t, x) — mj^ s=1______________________________d t

X ( z s ⁽ t , ^x ) s = 1

-

m (2)4 ^d z s ⁽ t , x ) ^s ) a t

—

—

V 2

X( z s ( t , x )^— m s 9 s = 1

Д ( z s ( t , ^x ) - m s ⁾) s = 1

^в 2 +

^{— e} 1 ⁺

X ( s=1

— 4

X (

s = 1

,                     = X

X( zs (t, x)—ms})

s = 1

+            = X

i X( zs(t, x)—ms’)

zs

z s ( t , ^x ) ^— m P^

a ^x 1

^d z s ⁽ t ■ x )

В ^x 2 ^s ⁽ ‘ ■ x )

V    ^d x 3    )

,

1 I ( x 1 I

^ U 1 + V 1 + W 1 ^л

1)

•

x ₂

V x 3 7

+

u ₂ + v ₂ + w ₂

V u ₂ + v ₂ + W 2 )

( t , x ) — m s '^TT)

—

^x{  X ( z s ( t , x ) ^— m s ²⁾) ^

s = 1

I 0 x 1 ^Sz s ⁽ t , x ) ^d x 2 ⁵ z s ⁽ t , x )

V    ⁵ x ₃    )

,

^л x 1 + 4 x ₂ + x ₃ + u 1 + v 1 + W 1

x 1 + x ₂ + x ₃ + u ₂ + v ₂ + W _{2 V} 2 x 1 — 4 x ₂ + x ₃ + u ₃ + v ₃ + W 3

, ( ^3.7 )

d*/\/d,/4.

— s ₃ ( t,x ) + (— s ₃ ( t , x ) ,Ax + u + v + w) = a t ^{3 (}, ) \a x ^{3 (}, ) ,                    /

X ( z s ( t , ^x ) - mS ) s = 1

в 1 +

X (z„( t, x)—msA^tx s =1                             d t

—

Д ( z s ( t , ^x ) - m s ⁽³⁾) s = 1

e +

4 Z( z ( t , ^x ) - m P)

/ 3 /

X\ E(zs(t,x)-mS3}-

\ s = 1

(SzsM ] Bxi dzs!t,x)

- X 2

,

4. Численный эксперимент

Численный эксперимент для данного примера проводится по схеме, аналогичной той, которая была применена в работе [4]. В частности, здесь полагается T = 1, компромиссные оценки принимаются равными

S 1 * = 0.8, S 2 * = 0.8, S 3 * = 0.8,

S 1 * = 0.9, S 2 * = 0.9, S 3 * = 0.9 ,

\                     l    ⁵ x 3

X + ^x 2 + ^x 3 + u 2 + v 2 + w 2

_v 2 x 1 - 4 x ₂ + x 3 + u 3 + v 3 + w ₃ J

J

а коэффициенты в гладких потенциалах – 37

1    2    3    200

Система неравенств, из которой определяется компромиссный набор стратегий, имеет вид

—s„ t , x +

+ mini — £ , ( t , x ) , Ax + u + v + w) >  0,

u * P \ x x                         /

—s„ t , x +

5 1 '

min (— s.„ ( t , x ) , Ax + u + v + w) >  0,

v * P \dx    ^{v 7}                /

— s* t , x +

+ min (— S 3 * ( t , x ) , Ax + u + v + w] >  0,

w * P \ xx                          /

51S1 (t,x) + d *

+ ( — s 1 ( t , x ) , Ax + u + v + w} <  0, ( 3.9 )

\ dx

В качестве начальной позиции выбрана точка (10, x10, x20, x30 ) = (0,0,0,0). Непосредственно проверяется, что s1 * (0,0,0,0) = s 2 * (0,0,0,0) = s 3 * (0,0,0,0) = = 0.815, s1* (0,0,0,0 ) = s 2* (0,0,0,0 ) = s 3* (0,0,0,0 ) = = 0.82.

Тогда начальная позиция удовлетворяет неравенствам

S 1 * <  s , * ( 0,0,0,0 ) < S i , i = 1,2,3.

— s * ( t , x ) +

— s* (t, x) + dt 31    ’

(— S 3 ( t , x ) , Ax + u + v + w) <  0 .

Рассмотрим последовательно следующие ситуации:

• а)    среди игроков нет уклонистов;

• б)    первый игрок уклоняется от компромиссного набора, прицеливаясь на свое целевое множество;

• в)    второй игрок уклоняется от компромиссного набора, прицеливаясь на свое целевое множество;

• г)    третий игрок уклоняется от компромиссного набора, прицеливаясь на свое целевое множество.

Управления уклонистов выбираем, как и в [4], в виде

ukl u ukl

Z ( m¹

—

xs

m

. ( 1 )

—

\

m

—

,

v ukl

1           ( 1 )

) l m 3

—

^x 3 J

Здесь левые части системы неравенств (3.9) вычисляются по формулам (3.2)–(3.8).

( 2 ) m 1 ( )

—

Z ( m?

—

xs

m

. (2)

—

,

1          ( 2 )

) l m 3

—

^x 3 J

( (3)       Л

^m (> - x 1

w u' ( I , x , , x 2 , x 3 ) = 3         — m 2’ ^- x 2 ^.

Длина временного полуинтервала при построении ломаных Эйлера принимается равной 8 = 0,001.

Результаты расчетов приведены в таблице, данные которой подтверждают факт принадлежности значения платы i -го игрока промежутку ] S i „ , S ’ ] , i = 1,2,3 для компромиссного набора стратегий. При этом уклонение игрока от этого набора не привело к достижению игроком-уклонистом величины платы меньшей, чем его нижняя компромиссная оценка (см. таблицу).

Игроки	Нижняя компро-мисcная оценка	Величина платы при уклонении	Величина платы для ком промиссной ситуации	Верхняя компром исcная оценка
Первый игрок	0,8	0,8343	0,8653	0,9
Второй игрок	0,8	0,803	0,9	0,9
Третий игрок	0,8	0,8058	0,9	09

Заключение

В статье приведен модельный пример, иллюстрирующий алгоритм построения компромиссного набора стратегий в линейной дифференциальной игре трех лиц с существенно более сложной динамикой, чем в аналогичном примере из работы [4]. Показана возможность применения этого алгоритма для случая линейной динамики игры, не являющейся "простым движением", и его эффективность для этого случая.