Построение математических моделей востребованности работодателями выпускников самарского государственного технического университета на основе рейтинга "Эксперт РА"

Алгоритм расчета рейтингового функционала состоит в следующем[4]:

• •    В соответствии с результатами экспертного опроса слушателей формируется список 100 ВУЗов, качество образования которых наиболее оценено наиболее высоко.

• •    По каждому из 100 ВУЗов формируется массив показателей в соответствии с предложенной системой оценки.

• •    По каждому показателю рассчитывается среднее по 100 ВУЗам значение (простое среднее арифметическое).

• •    Показатель каждого конкретного ВУЗа сравнивается со средним значением данного показателя для всех ВУЗов, по итогам сравнения конкретный показатель каждого ВУЗа оценивается по балльной шкале.

• •    Исходя из присвоенных балльных оценок по каждому из показателей, рассчитывается значение интегрального рейтингового фактора.

• •    Исходя из значений интегральных рейтинговых факторов и присвоенных им весовых коэффициентов (веса: качество образования – 0,5, востребованность работодателем – 0,3, научная и инновационная активность – 0,2) рассчитывается средневзвешенное значение рейтингового функционала.

• •    100 ВУЗов ранжируются в порядке убывания значения рейтингового функционала

  Рассмотрим показатели рейтинга «Эксперт РА» для СамГТУ. В табл. 2 представлены значения по рейтингу «Эксперт РА» для СамГТУ с 2012 по 2016 гг., а на рис. 1 – позиции СамГТУ в рейтинге [5, 6]. Позиции вуза улучшаются с каждым годом. В 2012 г. СамГТУ был на 84 месте, в 2013 – на 73, 2014 – 56, 2015 – 54 и в 2016 году вуз уже занимает 52 позицию.

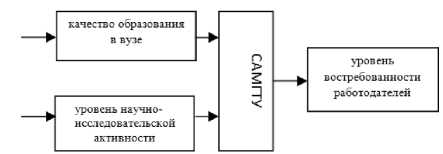
Построим модель востребованности работодателями специалистов, выпускаемых СамГТУ (рис. 2). В качестве входных факторов будим использовать показатель качества образования и уровень научно-исследовательской активности, выходом будем считать уровень востребованности работодателями. Для построения модели будем использовать данные из рейтинга «Эксперт РА».

Таблица 1. Веса факторов рейтинга «Эксперт РА»

Качество образования в ВУЗе				Уровень востребованности работодателями выпускников ВУЗа		Уровень научноисследовательской активности ВУЗа
0,5				0,3		0,2
урове нь преп одава ния	межд унаро дная интег рация	ресур сное обесп ечени е	востребо ванность среди абитурие нтов	качество карьеры выпускн иков	сотрудни чество с работода телями	инновац ионная активнос ть	научны е достиж ения	инновацио нная инфрастру ктура
0,25	0,25	0,25	0,25	0,5	0,5	0,5	0,3	0,2

Таблица 2. Показатели рейтинга «Эксперт РА» для СамГТУ по годам

Год	Качество образования	Научноисследовательская активность	Востребованность работодателями
2012	108	75	44
2013	113	66	29
2014	92	56	25
2015	100	49	23
2016	76	66	29

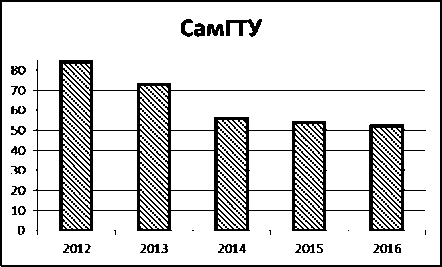
Рис. 1. Позиции СамГТУ в рейтинге «Эксперт РА»

где Y – уровень востребованности выпускников СамГТУ в расчетный год работодателями; K – показатель качества образования; V – уровень научноисследовательской активности; A – масштабный

коэффициент; α , β - функции эластичности.

Преобразуем исходные данные в обратные величины по формуле (2):

-1т/-1

K = V = Y =

¹ К ; ¹ V ; ¹ Y

;

;

Построим модель востребованности работодателями специалистов, выпускаемых СамГТУ (рис. 2). В качестве входных факторов будем использовать показатель качества образования и уровень научно-исследовательской активности, выходом будем считать уровень востребованности работодателями. Для построения модели будем использовать данные из рейтинга «Эксперт РА».

где Y 1 – обратная величина уровня востребованности выпускников СамГТУ в расчетный год работодателями; K 1 - обратная величина показателя качества образования; V 1 – обратная величина уровня научно-исследовательской активности.

Исходная модель (1) на основе ПФ в форме Кобба–Дугласа примет следующий вид:

Y₁ = AK “V ^e

Оценка адекватности исходных статистических данных и модели производится по критерию Дарбина-Уотсона и коэффициенту автокорреляции, которые находятся по формуле (2) и (3) соответственно.

d =

Рис. 2. Модель востребованности выпускников работодателями

n

^ (( y i ^- у и ) ^- ( y - 1 ^- y и - 1 ⁾⁾²

i = 2

n

Z ( У , - У т )²

I = 1

где Уi, У, -1 - действительная востребованность;

Построим модель с учетом влияния указанных факторов на основе производственной функции (ПФ) в форме Кобба–Дугласа:

y и , y и -1 - расчетная востребованность выпускников СамГТУ; n - объем выборки. Допустимый интервал для критерия Дарбина-Уотсона изменяется в пределах 0< d <4.

Y = AK ^α V ^β

ra

= 1 -

d

,

где d - статистика Дарбина-Уотсона.

Для измерения мультиколлинеарности - попарной корреляционной зависимости между факторами, используют коэффициент множественной детерминации:

Е(^-У,т)2

Я2=1--4------

Коэффициент К² показывает, какая доля дисперсии результативного признака объясняется влиянием объясняющих переменных. Если связь отсутствует, то Д³=0. Коэффициент детерминации не определяет, увеличивается ли или уменьшается выход с ростом входа. Функциональная связь возникает при значении равном 1, а отсутствие связи - 0 [7, 8].

С помощью линейного регрессионного анализа по методу наименьших квадратов (МНК) рассчитаем параметры модели на четырехлетием временном интервале (с 2012 по 2015 гг.) по несгла-женным и сглаженным значениям. Применим метод сглаживания ряда по трем точкам. В табл. 3 и на рис.З и 4 представлены две получившиеся модели. Коэффициент корреляции близок 1 и равен 0,8463 и 0,9997 соответственно для несглаженной и сглаженной модели. Критерий Дарбина-Уотсона находится в допустимом диапазоне и равен 2,3 и 2,1 соответственно.

Таблица 3. Параметры и характеристики моделей ПФ Кобба-Дугласа за 2012-2015 гг.

Параметры модели	Неслаженные данные	Сглаженные данные
1п(А)	1,5398	1,3455
а	-0,3168	-0,1126
Р	1,4781	1,6484
d	2,3	2,13
Ra	-0,15	-0,23
R2	0,8463	0,9997

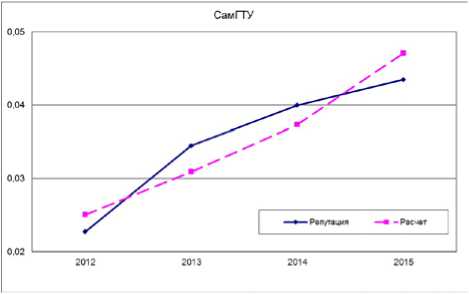
Рис. 3. Модель востребованности

Значения эластичности по качеству образования равны -0,31 и -0,11 соответственно, а эластичность по уровню научно-исследовательской активности равна 1,47 и 1,64. При этом р>а, что отражает больший вклад научно-исследовательской активности на уровень востребованности работодателей. При увеличении показателя качества образования на 1%, уровень востребованности работодателей снижается на 0,3% и 0,1% соответственно.

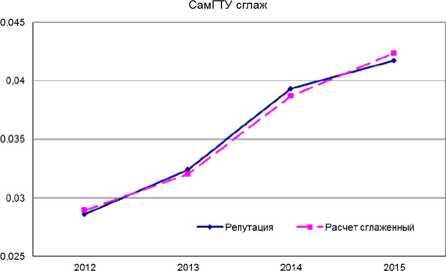
Рис. 4. Сглаженная модель востребованности

В целом модель, идентифицированная на интервале 2012-2015 гг., достаточно удовлетворительно описывает тенденцию функциональной взаимосвязи между входными и выходными характеристиками рейтинга «Эксперт РА» и исходных данных. По сглаженной модели расчеты практически точно совпадают с исходными данными. Модель является адекватной анализируемым процессам. Добавим в модель данные по 2016 г., построим прогноз и сравним с действительными данными по 2016 г. В табл. 4 и на рис. 5 и 6 представлены полученные модели. Качество модели получилось очень хорошее. Построенная модель с достаточной точностью описывает уровень востребованности работодателями в течение года. Коэффициент корреляции увеличился и достигает значение 0,99, почти равен 1.

Таблица 4. Параметры и характеристики моделей ПФ Кобба-Дугласа за 2012-2015 гг. с прогнозом

Параметры модели	Неслаженные данные	Сглаженные данные
1п(А)	1,4781	2,4634
а	-0,3168	0,00487
Р	1,5399	1,4091
d	2,7058	2,022
Ra	-0,35291	-0,0113
R2	0,992674	0,9999

Величина критерия d=2,7 и d=2,02 свидетельствует об отсутствии автокорреляции остатков, следовательно, зависимость (3) обладает высокими прогнозными свойствами. Однако по модели, построенной по реальным данным, видно, что востребованность работодателей в 2016 г. находится на уровне 2013 г., что видно также из исходных данных и табл. 2, а по сглаженной модели не наблюдается. Это связано с усреднением исходных данных. По несглаженной модели данные получаются более реальные.

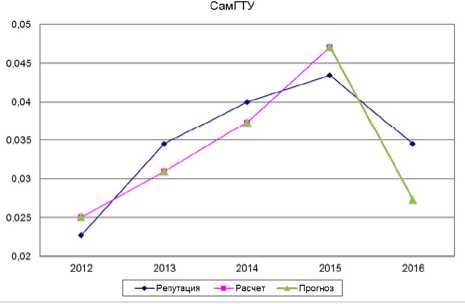
Рис. 5. Несглаженная модель с прогнозом

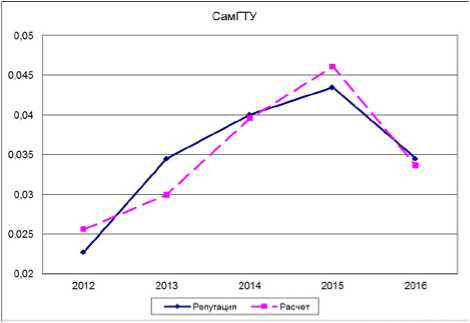
Рис. 7. Несглаженная модель с 2012 по 2016 гг.

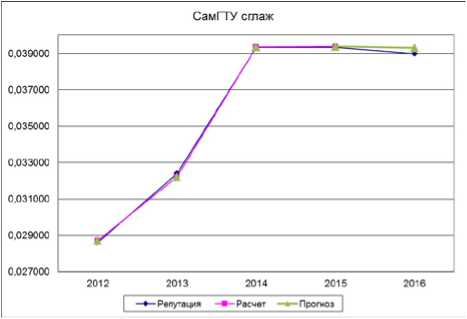
Рис. 6. Сглаженная модель с прогнозом

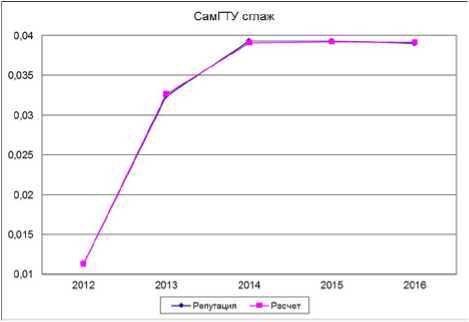
Рис. 8. Сглаженная модель с 2012 по 2016 гг.

Таким образом, показатели качества производственной функции определяют возможность ее применения для исследования уровня востребованности работодателями выпускников СамГГУ. Построим модель по реальным данным за период с 2012 по 2016 г. В табл. 4 и на рис. 7 и 8 представлены полученные модели. Значения эластичности по качеству образования повысились и стали положительны. При этом так же р>а, что отражает больший вклад научно-исследовательской активности на уровень востребованности работодателей.

Таблица 5. Параметры и характеристики моделей ПФ Кобба-Дугласа за 2012-2016

Параметры модели	Неслаженные данные	Сглаженные данные
1п(А)	3,4187	1,922
а	0,29	0,0237
Р	1,325	1,2557
d	2,616	2,966
Ra	-0,308	-0,483
R2	0,9931	0,9999

Построим модель с 2012 по 2016 г. и предположим, что входные параметры в 2017 г. поменяются по сравнению с 2016 г., качество образование в вузе станет 70, т.е. на 8% снизится и уровень научно-исследовательской активности станет 60, что на 10% ниже значения в 2016 г. в рейтинге «Эксперт РА». На рис. 9 и 10 представлены полученные модели.

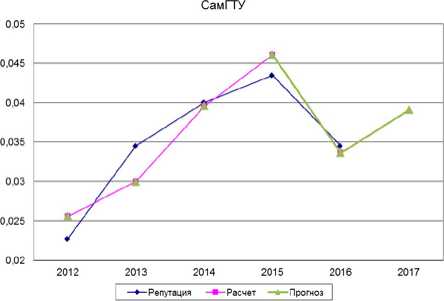
Рис. 9. Несглаженная модель с 2012 по 2016 гг. с прогнозом на 2017 г.

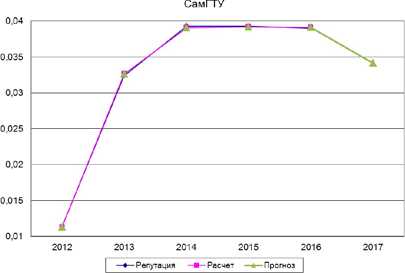
Рис. 10. Сглаженная модель с 2012 по 2016 гг. с прогнозом на 2017 г.

По несглаженной модели показатель уровень востребованности работодателями снизится до 26, что на 13% ниже показателя 2016 г., а вот по модели, построенной по сглаженным данным, показатель повыситься на 1%, и будет равен 29,3. Можно сделать вывод, что при улучшении показателя качество образование в вузе на 50% до 38 при неизменном уровне научно-исследовательской активности, равной 66, показатель уровня востребованности работодателями составит 24, а при неизменном уровне образовательной деятельности и при уменьшении на 50% научно-исследовательской активности, уровень востребованности работодателями составит 12. Данные значения показателей свидетельствуют о большем влиянии научно-исследовательской активности на уровень востребованности работодателями.

Выводы: все построенные агрегированные модели достаточно точно описывают тенденцию функциональной взаимосвязи между показателем качества образования и уровнем научно-исследовательской активности рейтинга «Эксперт РА» и могут быть использованы в качестве имитационных моделей для получения управленческих решений. Анализ коэффициентов эластичности показал, что больший вклад на уровень востребованности работодателей оказывает научно-исследовательская активность, что можно объяснить хоздоговорными работами. В них обычно кроме преподавателей участвуют студенты, при этом к окончанию вуза они приобретают существенный научный и практический потенциал, авторитет и связи с промышленными предприятиями и научными объединениями. Большинство студентов на старших курсах уже работают по специальности. А готовых специалистов, знакомых со спецификой производства, работодатели с большим удовольствием принимают на работу [9].