Построение наилучшей гарантирующей стратегии игрока в одной антагонистической игре с недифференцируемой ценой

Известно, что функция цены в антагонистических дифференциальных играх является непрерывной, но необязательно непрерывно дифференцируемой функцией. В случае ее дифференцируемости эффективным методом построения оптимальных стратегий игроков служит принцип перехода Р.Айзекса [1], реализация которого сводится к интегрированию дифференциального уравнение Беллмана – Айзекса. В противном случае строить допустимые (гладкие) позиционные стратегии игроков, обеспечивающие седловую точку в игре, не удается.

В книге [2] указанные стратегии реализуются в форме экстремального прицеливания на соответствующие стабильные мосты. В статье на примере конкретной дифференциальной игры с недифференцируемой ценой демонстрируется возможность применения данного подхода для ее решения

1. Постановка дифференциальной игры

Рассмотрим динамический конфликтно управляемый объект

X j = x ₃, X ₂ = x ₄, x ₃ = u + v , x ₄ = u ₂ + v ₂, (1.1) t e [ t o , T ] , x 1 ( 0 ) = x _w, X 2 ( 0 ) = x 20 ,

^X 3 ( ⁰ ) = ^X 30 , ^X 4 ( ⁰ ) = ^X 40 ,

и =

u 1

< u 2 >

e P = {u e R2| ||u|| < a} ,

v =

v ₁

v

e Q = {v e

R2| И < в} ,0 < в < а,

I [и fl, и И = 4 x 2 (T) + xI (T).

Здесь x =

x1 x x3 x

e R ⁴ — фазовый вектор игры,

t e [ t₀ , T ] — текущее время, и , v e R ² - векто-

ры управляющих параметров первого и второго игроков соответственно, I — функция платы, минимизируемая первым игроком и максимизируемая вторым игроком.

Описанная здесь конфликтная ситуация допускает следующую физическую интерпретацию. Материальная точка единичной массы, управляемая двумя игроками, движется по

гладкой горизонтальной плоскости. Каждый игрок в любой момент времени может воздействовать на точку, прикладывая к ней силу, произвольную по направлению и ограниченную по величине. Цель первого игрока – минимизировать в конечный момент времени геометрическое расстояние от управляемой точки до начала координат, а второго игрока – максимизировать это расстояние.

2. Принцип перехода Р. Айзекса

Предполагая, что цена игры является дифференцируемой функцией позиции, будем искать ее как решение дифференциального уравнение Беллмана – Айзекса [1]

max

+в

de

de⁰  de ⁰

--1-- dt    dx.

+ ( ^{в - a} )

id e

V [dx

+

de dx.

= 0 ,

de° .     _

--+ min max

de0

d t

u e P  v e Q

5 x i

de3

+ Л-- x4 + dx 2

de

3 +t^

dx.

' 3 )

x 4 +

+

de0

d x _{4 4}

= 0 . (2.3)

Последовательность операций min и в (2.1) допускает обратную замену, а

управления, на которых указанные min и max достигаются, имеют вид u0[t,x] — -a-R(t,x) , v0[t,x] = fi-R(t,x),

de ⁰_t      . de ⁰

+--(Ui + Vi) +-- dx-              dx4

( u ₂ + v 2 ) = 0

R ^{( (} t , ^x ) ) =

(2.1)

I de ⁰ J²

+

Ide ⁰ J²

3 )

^d x 4

)

(e J a . з

Ц1

^ О x 4 )

. (2.4)

с граничными условиями e0 (T, x 1, x 2, x 3, x 4

x j + x₂ .

(2.2)

Пусть

Ide ⁰J²

Id x ₃ J

+

Ide ⁰J²

Id x 4 J

^ 0.

Преобразуем выражение

de0 ,     _

=--+ min max dt    ueP  veQ

de

d x i

x

de0

+ ~— x4 + dx 2

de ⁰  ,        . de ⁰

+--(u1 + Vi)+-- dx3             dx4

( u 2 + ^v 2 ) = 0.

Последовательно вычисляем:

de ⁰   de⁰

d t     d x.

d e⁰

+ — x4 + dx2

+ min

de0

^{u e P} |_ dx₃

u

de0

+--u3

d x 4  ²

+

+ max

de0

de0

---V +--v

dx3

dx4

= 0 ,

de ⁰   de⁰

d t     d x.

de0

x ₄

^d x 2

—

-a

de ⁰ Y

V [d ^x 3 )

+

de ⁰ Y

dx.

+

Заметим, что равенство

\   de0   de0

F ( t , x ) — + ^{y J}    dt    dx,

de0

x +--x + dx2

⁺ ( ^{в - a} )

id e у [a x

' 3 )

+

имеет место и в случае, когда

de dx,

+

de0

d x 4 )

J ²

= 0

e ] ² dx. ,

= 0.

Функцию e ⁰, являющуюся решением задачи

(2.1), (2.2), будем искать в виде

e

( t , x 1 , x ₂, x ₃, x 4

) =

— a <^[ x + ( T — t ) x^ ) ^ + [ x ₂ + ( T — t ) ^X4 ] +

h ( t — t )2 +b-----—, где a, b e R1 - постоянные, подлежащие определению.

Построение функции e ⁰ будем производить в области

Z — { ( t , x )| t e [ 1 0 , T ] , [ x i ( t ) + ( T - 1 ) x з ( t ) ] ² + + [ x ₂ ( t ) + ( T — t ) x₄ (t ) ] } > 0 .

Из граничных условий (2) следует, что a — 1 .

Тогда

де0

^“

д t

XX + x₂x ₄ + ( T - 1 ) ( x ₃ ² + x 2 )

2                        “12 ⁺

де0

дx x + x3 (T -1)

[ ^X 1 ⁺( ^{T - 1} ) ^X 3 ) ] ⁺ [ ^X 2 ⁺( ^T — ¹ ) ^X 4 ] д е⁰

д x₂

x ₂ + x ₄ ( T — 1 )

[ Xj +(T — 1) x3)] + ^ x2 + ( T — 1) x4 J де0

дx3

[ X 1 + x 3 ( T — 1 ) ] ( T — 1 )

^ x 1 + ( T — 1 ) x ₃) ] +1^ x ₂ + ( T — 1 ) x ₄ ] д е⁰

В области Z управления u ⁰ [•] , v ⁰ [•] , вычисленные по формулам (2.4) с учетом (2.5), допустимы и, следовательно, оптимальны. При этом

I [ u “ [ • ] , v 0 [ • ] ] = е ⁰ ( 1 0 , X 0 ) —

[ ^X 10 ⁺ ( ^{T — 1} 0 ) ^X 30 ) ] ⁺[ ^X 20 ⁺ ( ^{T — 1} 0 ) ^X 40 ] ⁺ + ( в — a 'fT—^ .

Пример 1.   Полагаем     a = 5, в — 1, t 0 = 0 , T — 1,    X10 = 1 , X20 = 1 ,

X ₃g — 0.5, x ₄₄ — 0.5.

Рассмотрим три случая:

• 1)    оба игрока действуют оптимально (выбирают свои стратегии в соответствии с формулами (2.5));

• 2)    первый игрок действует оптимально, а второй придерживается произвольного допустимого программного управления, напри-

  мер управления

  
  

  v ( ^{1 ) —}

  
  

  ^ в • sin 31

  _ч в • cos3 1 ₂

  
  

  1 e [ 0,1 ] ;

  
  

• 3)    второй игрок действует оптимально, а первый придерживается произвольного до-

  д x ₄

  _         [ X 2 + X 4 ( T — 1 ) ] ( T — 1 )

  J+^-tX)^f7 2 +T^^ ^.

  Подставим найденные частные производные функции е⁰ в уравнение (2.3). В результате получим

  
  

  пустимого программного управления, напри-

  
  

  мер, управления

  
  

  u ( 1 ) —

  
  

  ^г — a • sin 3 1^Л _v— a • cos3 1 _y

  
  

  , 1 e [ 0,1 ] .

  
  

  — b ( T — t ) + ( в — a )( T — t ) — 0 ^ b = в — а .

  
  

  Таким образом,

  
  

  е

  
  

  ( 1 , X 1 , x ₂, x ₃, x ₄

  
  

  ) =

  
  

  ^X +'( T - ^ ) x j)] + [ x ₂ + ( T — 1 ) x ₄ ] + ⁺ ( ^{в — a} ) ⁽ T ₂¹ ) , R ( 1 , x 1 , x₂, x₃, x ₄ ) =

  ^X H T —o x oH x T^^

  
  
  
  
  

  ^ X + ( T — 1 ) x₃^Л , x 2 + ( T ^{— 1} ) ^x 4 _y

  
  

  (2.5)

  
  

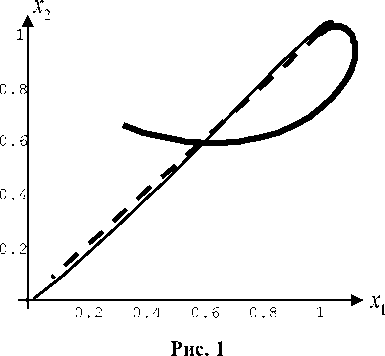
  На рис. 1 показаны траектории движения управляемой точки на плоскости для всех трех случаев. При этом в случае 1) траектория обозначена пунктирной линией, в случае 2) – жирной линией и в случае 3) – обычной линией.

  
  

• 3.    Стабильный мост и экстремальное прицеливание

Тот факт, что пара стратегий u ⁰, v ⁰ образует седловую точку в игре, подтверждается двойным неравенством

I [ u 0 , v ] = 0.0238062<0.12132= I [ u 0 , v 0 ] <

<0.734656= I [ u , v ⁰].

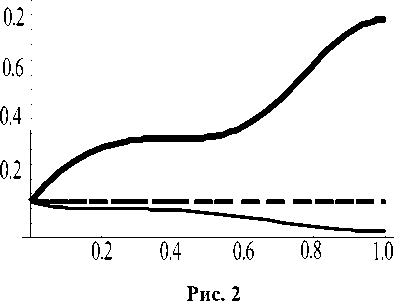
Функция s⁰ должна оставаться постоянной вдоль траектории движения для первого случая, монотонно убывать для второго случая и монотонно возрастать для третьего случая. Указанные зависимости функции s⁰ от времени приведены на рис. 2.

Вне области Z позиционные стратегии игроков (2.4), (2.5) уже не являются допустимыми, а цена игры - функция s ⁰ перестает быть непрерывно дифференцируемой функцией. В случае, когда в процессе игры ( t , x [ t ] ) ^ Z дифференциальное уравнение (1.1) при подстановке в него позиционных стратегий (2.4), (2.5) игроков не может быть проинтегрировано.

Покажем, что для начальных позиций ( t ₀, x ₀ ) ^ Z первый игрок, применяя экстремальное прицеливание на подходящий стабильный мост, в состоянии привести управляемую точку в начало координат при любых противодействиях второго игрока, т.е. получить наилучшее для себя значение платы.

Полагаем

W ={(t,x)|s° (t, x)< 0} •

Очевидно, что множество W_u обладает следующими свойствами

• 1)    W . ( T ) = { x ( T . x ) e W . } =•

  
  

• 2)    для любых { t , , x , } e W_u , v * e Q,

t *e( t,, T ] x (•) = x (•, t,, x,, v ’) существует решение дифференциального уравнения в контингенциях x1

= x ₃, x ₂ = x ₄,

eP + v’, t e[t,,t*], x(t,) = x, такое, что x(t’) e Wu (t*) = {x|(t*,x) e Wu} •

Таким образом, множество W представляет собой стабильный мост первого игрока, обрывающийся в финальный момент времени в начале координат.

Определим U ^e стратегию первого игрока, осуществляющую экстремальное прицеливание на стабильный мост W . u

Пусть x ^ W_u , t e [ t ₀, T ] . Найдем вектор p_t из условия ll x - p j 1= min ll x - p ll • p e W_u ( t )

Для этого решим задачу математического программирования на условный минимум с ограничением типа неравенства

JE( P i - x^ ^ min ,

V i = 1

у/[pl + (T - t) p3)] +[p2 + (T - t) p4 ] +

+ (в - a)(T - t)<

Эта задача эквивалентна следующей задаче:

( p i ^- x l ) 2 ⁺( p 2 ^- x 2 ) 2 ⁺

+ (p3 -x3)2 +(p4 -x4)2 ^min,(3.1)

[pi +(T-t)p3)] +[p2 +(T-t)p4]

t - 1

• -(a - в)           0.(3.2)

Составим для нее функцию Лагранжа

L ( p i , p 2 , p 3 , p 4 , ^ ) =

= ( pl - xl ) +( p 2 - x2 ) +

+ (p3 -x3 ) + (p4 -x4 ) +

Заметим, что

+A^[ pi +( T - t ) p3)] + [ p 2 + ( T - t ) p 4 ] -

u e ( t , x )

= -a •

s 3 ( t , x )

s ₃ ² ( t , x ) + s 2 ( t , x )

-(a - в)2

u ^ ( t , x )

= -a •

s 3 ( t , x )

yjs32 (t, x ) + s4 (t, x )

и выпишем необходимые условия экстремума

— = 2 ( P

'Pi       V 1

- xi) + 2 [Pi + pз (T -1)] A = 0,

" = 2 (P ap2    211

- x2) + 2 [p2 + p4 (T -t)] A = 0,

Окончательно устанавливаем, что

Ue (t, x ) = ue (t, x),           x ^ Wu (t), произвольный u e P,  x e Wu (t)

(3.3)

5 L

^d P 3

= 2(p3 -x3) + 2(T-1)[p1 + p3 (T-1)] A = 0, dL dp 4

= 2 ( p4 - x4 ) + 2 ( T - t )[ p 2 + p4 ( T - t )] A = 0.

Управление точкой первый игрок осуществляет по следующей схеме. Интервал времени [ 0, T ] разбивается на полуинтервалы [ ТТ + i ) , i = ⁱ,², - .

Добавляя к полученным уравнениям условие связи (3.2), получим систему из пяти уравнений относительно неизвестных p i , p 2 , p 3 , p 4 , ^A •

Ее решение p * , p 2 , p ₃ * , p 4 , A *, полученное средствами пакета Mathematica, весьма громоздко и здесь не приводится.

Можно показать, что набор величин p * , p 2 , p з , p 4 действительно доставляет условный минимум в (3.1), (3.2).

Полагаем

На каждом из таких полуинтервалов управление первого игрока считается постоянным и равным U^e ( р , x ( т ) ) = const , а управление второго игрока – произвольной допустимой реализацией вектора его управляющих параметров. Равномерный предел соответствующих ломаных Эйлера будет являться движением рассматриваемой точки, порожденным стратегией (3.3) первого игрока.

В книге [2] показано, что каждое такое движение будет оставаться на множестве W вплоть до момента времени T . Последнее обстоятельство обеспечивает наилучший результат в игре для первого игрока.

^ ^ з ( t , x )^л s ₂ ( t , x ) s 3 ( t , x ) ч s 4 ( t , ^x ) >

*A ^x i ^- p i

*

x 2 - p 2

*

^x 3 ^- p 3

ч ^x 4 - p 4 y

Пример 2. Пусть a = 7 , в = 2 , 1 0 = 0,

T = ¹ , ^x i0 = ⁱ , x 20

= i, x ₃₀ = 0.5, x ₄₀ = 0.5.

Заметим, что начальная позиция принадлежит множеству W_u . Тогда стратегия (3.3) обеспе-

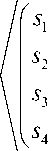
( t , x )' ( t , x ) ( t , x )

⁽ t , x L

ue

4 u 2

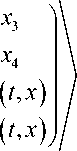
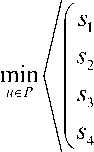
( t , x )^Л ( t , x ) ( t , x )

⁽ t , ^x L

u

ч ^u 2

( t , x ) ⁽ t , x ) y

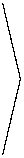
чивает значение платы в игре, равное нулю, т.е. переводит геометрические координаты точки в начало координат в конечный момент времени.

Движение точки, порожденное управлением (3.3) первого игрока, аппроксимируем ломаными Эйлера, построенными на разбиениях интервала времени [ 0,i ] на 20, 50 и 80 частей.

Плата на каждой из этих аппроксимаций принимает соответственно значение

I ₂₀ = 0.034i, I ₅₀ = 0.0i37,

I ₈₀ = 0.0043.            (3.4)

На рис. 3 показана траектория движения точки, построенная на базе ломаной Эйлера для 80 разбиений.

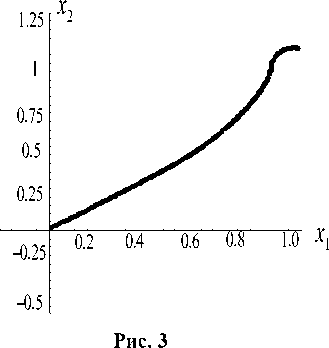
В отличие от предельного движения аппроксимирующая его ломаная Эйлера может в некоторые моменты времени покидать мно-

жество W . Это обстоятельство объясняет тот факт, что значение платы для ломаных Эйлера не является чистым нулем. Однако, как это видно из (3.4), в пределе величина платы стремится к нулю.

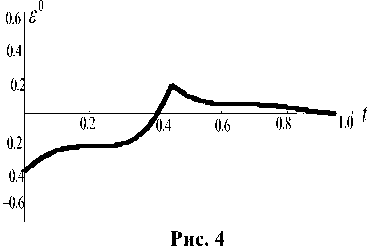
На рис. 4 приведен график изменения функции ε , вычисленной вдоль ломаной Эйлера, в зависимости от времени. В моменты времени, для которых ε >  0 позиция выходит за пределы множества W_u

Заключение

Таким образом, в игре с недифференцируемой ценой построена наилучшая гарантирующая стратегия первого игрока в форме прицеливания на стабильный мост. При этом указанная стратегия оказалась разрывной по фазовому вектору игры. Применение пакета Mathematica позволило получить ее аналитическое выражение. Проведенные численные эксперименты подтвердили оптимальность построенной стратегии.