Построение спектральной плотности решения линейного стохастического дифференциального уравнения в частных производных с постоянными запаздываниями

Предисловие

Необходимость математического моделирования роста растений связана с земледелием двояко: с одной стороны – для обеспечения текущих потребностей агротехнологии выращивания культурных растений (продуктов питания), с другой стороны – для селекционной работы по выведению новых, более продуктивных и более приспособленных к внешним условиям сортов растений. Понятно, что широта (в отличие от узкоспециализированно-сти) применения матмоделей обеспечивается их простотой и простотой интерпретации их параметров. Ниже описаны достаточно простые модели роста однолетних растений, использующие аппарат классической теории автоматического управления.

1.    "Дифференциальный" подход к моделям

Исторически сложилось так, что математические модели роста растений рассматривались как модели скорости роста биомассы, например: "для свободно растущего рас-

тения две функции возраста Аj(t) – количество средств существования j-го типа и B(t) – скорость роста биомассы свободно растущего растения возраста t" [1, с. 715]1, где B(t) может быть вектором, учитывающим рост биомассы отдельных органов растения (корней, листьев, стеблей, плодов и т. п.). В такой "дифференциальной" форме модель представляла собой систему дифференциальных уравнений, и если в модель вводилось управление (для получения максимальных урожаев), то оно, соответственно принципу максимума Понтрягина, давало решение на границах допустимой области управлений: максимум допустимой освещенности, максимум допустимого полива, максимум допустимых доз минеральных удобрений2 и т. п. Однако не всеми параметрами можно управлять, особенно это касается климатических параметров, и задача селекции – получение сортов, продуктивных как раз в неоптимальных условиях роста растения (эта общая задача практически неизменна за всю историю селекции [15]).

Проблемы получения математических моделей роста растений отмечались как в 1980–1990-е гг.: "В настоящее время <1990-е гг.> одним из главных препятствий на пути целенаправленного создания агрохимически эффективных сортов является отсутствие моделей как концептуального уровня, так и основанных на экспериментальных данных" [3, с. 302], – так и в недавнем прошлом: "необходимо отметить заметный скепсис ученых-физиологов по поводу возможностей современных математических дисциплин при моделировании продукционных, в том числе и ростовых процессов" [6, с. 103].

Одним из препятствий построения математических моделей роста растений является как раз "дифференциальная" форма модели, затрудняющая интерпретацию и идентификацию параметров модели. "Эмпирические параметры <дифференциальных> уравнений также несут на себе отпечаток случайности и не могут с большой степенью достоверности использоваться для прогнозирования темпов роста растений и формирования урожая" [6, с. 103].

Пример одной из "дифференциальных" моделей роста растений, многократно проверенный на экспериментальных данных приведен ниже.

2.    Пример модели и данных

Информационная структура математической модели роста картофеля [11] показана на рис. 1.

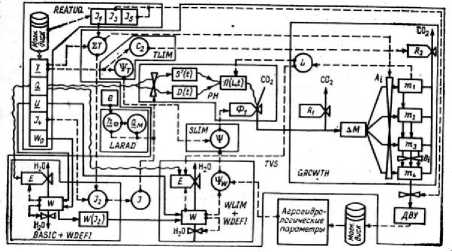
Рис. 1. Структура модели роста картофеля, по [11, с. 86]

Однако ключевым для модели является представление данных в этой модели, пример эмпирических данных и модельного приближения приведен на рис. 2 в виде относитель- ной биомассы органов растения, приведенной в каждый момент роста к 1, показывающей в "дифференциальном" виде скорость роста от-3

дельных органов растения.

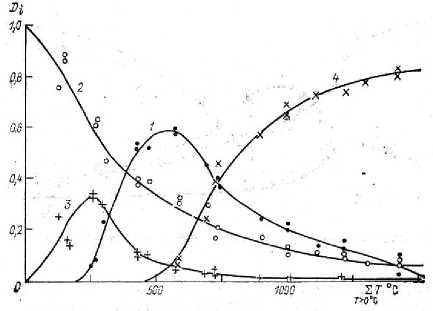
Рис. 2. Данные и результат моделирования для картофеля сорта Белорусский ранний, относительные биомассы: 1 – листья, 2 – стебли, 3 – корни, 4 – клубни, по [11, с. 86] ( по горизонтали – сумма средних температур за день, больших 0 ° С)

Значительная нелинейность функций роста, представленных на рис. 2, затрудняет их сопоставление с действительными процессами роста растения. Если же данные рис. 2 проинтегрировать и привести к виду перенормированному к 1 относительно накопленной к концу роста (сбору урожая) биомассе, то получается простая картина (см. рис. 3, 4).

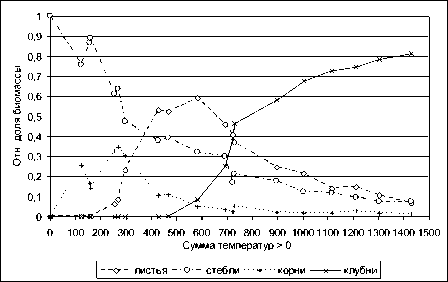
Рис. 3. Экспериментальные данные из рис. 2, [11, с. 86], "дифференциальная" форма

• ³    О функциях роста в аналогичной форме см. также [12, с. 67].

4.    Модель растения как конечная система 5.    Модель роста как конечный набор звеньев

Более современные модели, хотя и отображали результаты в "интегральной" форме [8, с. 330, рис. 7.4], но для моделей использовали функции роста в дифференциальной форме [8, с. 299–300], см. также п. 2.

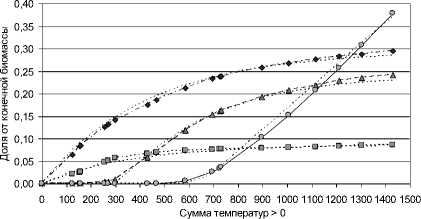
-4- листья -■■♦■- стебли ------- корни          клубни стебли_м      корни_м       листья_м      клубни_м

Рис. 4. Проинтегрированные данные из рис. 2, 3 , "интегральная" форма, относительно конечной биомассы, принятой за 1

Кривые на рис. 4 содержательно понятны относительно предметной области (накопления органами растением биомассы), и, кроме того, по теории автоматического управления кривые на рис. 4 хорошо приближаемы функциями реакции на единичное воздействие типовых динамических звеньев (1–2-го порядка) и их комбинаций. О том, почему содержательно допустимо такое приближение, сказано ниже.

Хотя в фундаментальном смысле геномом (и вообще наследственностью) не определяются полностью свойства живого организма (в частности свойство быть живым)4, для прикладных целей, в том плане, что имеется дело с живыми организмами в благоприятной для них среде, с определенным набором протекающих в них и между ними и окружающей средой процессов, в первом приближении модель растения выглядит как конечная система, описываемая приближенно некоторой совокупностью линейных звеньев порядка не выше 2. В этой модели генотип и окружающая среда рассматриваются неразрывно, соответственно высказанным еще в середине XX в., и многократно проверенным к нач. XXI положениям биологической нау-ки5. Таким образом, взгляд на рост растения как на определенный и генотипом и средой некий переходный процесс от начального до конечного состояния (с перенормировкой по конечному состоянию) позволяет усматривать в этом процессе некие достаточно простые закономерности.

В простой модели роста растения его рост рассматривается как реакция на единичное воздействие (функцию 1(t)), соответствующее моменту времени t0 – посеву семени в почву (при благоприятных для роста внешних условиях). Тогда рост органов растения как реакция на это воздействие есть комбинация функций типовых звеньев: запаздывающего звена, апериодического звена, интегрирующего звена (см. [9], [4]). Тогда для "интегральных" данных приведенных на рис. 4 функции модели роста картофеля (см. рис. 2–4) таковы, как указано в таблице: листья – апериодичес-ское звено с запаздыванием; стебли – апериодическое звено; корни – апериодическое звено; клубни – интегрирующее звено c запаздыванием. (На рис. 2–4 физическое время заменено на "биологическое" – сумму температур, что не меняет вида закономерностей; условное время обозначено за t).

Кроме того, имеется общий коэффициент модели k0, переводящий относительные величины рис. 4 и таблицы (h1–h4) в конечную (на сбор урожая) биомассу в ц/га.

По рис. 4 и таблице легко видеть, что запаздывание роста клубней примерно равно двойному запаздыванию роста листьев, относительно начала роста, τ4≈2τ1. Постоянные ни, своего развития и определённо реагировать на те или иные условия" [5]. К концу XX – нач. XXI в. единство в жизни растения генотипа и условий среды было опытно подтверждено, вплоть до влияния среды на генотип, а именно была "показана способность растений пшеницы (а может быть и всего класса эукариот) к переопределению генетических формул сорта под влиянием обеспеченности элементами питания и другими факторами среды, как <…> механизм неспецифической природы" [3, с. 296], необходимый для сохранения вида. И, ближе к современности, установлено, что "изменение определенных условий окружающей среды приводит к изменению локализации <в геноме> QTL (хозяйственно-ценных признаков), вовлеченных в реализацию некоторых признаков <у яровой мягкой пшеницы>" [13, с. 65].

времени (T 1 –T 3 ) роста служебных органов (не урожая) приближенно равны.

Функции модели для отдельных органов

Орган	Формула реакции на 1(t)	Параметры*
Листья	h 1 (t)= 1( τ 1 ) ⋅ k 1 (1–exp(–(t– τ 1 )/T 1 )	k 1 =0,229; Т 1 =370; τ 1 =320
Стебли	h 2 (t)= 1(0) ⋅ k 2 (1–exp(–t/T 2 )	k 2 =0,284; Т 2 =420
Корни	h 3 (t)= 1(0) ⋅ k 3 (1–exp(–t/T 3 )	k 3 =0,084; Т 3 =370
Клубни	h 4 (t)= 1( τ 4 ) ⋅ k 4 (t– τ 4 )/T 4	k 4 =0,371; Т 4 =2100; τ 4 =650

*k i – безразмерны, Т i , τ i – в условных единицах биологического времени, для данных рис. 2–4 – сумма дневных температур, больших 0

Какие параметры столбца 3 таблицы, и в какой мере определяются генотипом и условиями роста – подлежит отдельному опытному определению для конкретных сортов рас-тений6.

Модель позволяет определить особенности роста урожая, в отличие от роста других органов: рост урожая описывается интегральным звеном с запаздыванием.

6.    Примеры приложения модели

Примеры интерпретации модели приведены по оцифрованным интегрированным с перенормировкой данным. Для ячменя получается следующая картина (рис. 5): – "дифференциальные" данные (из [10]), понимание затруднено; рис. 6 – проинтегрированные данные, интерпретация аналогична таковой в п. 5.

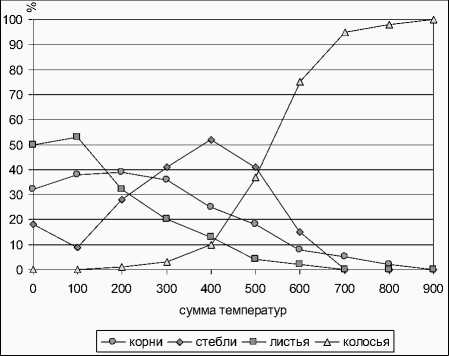
Рис. 5. Функции текущей приведенной к 1 биомассы для ячменя, по [10]

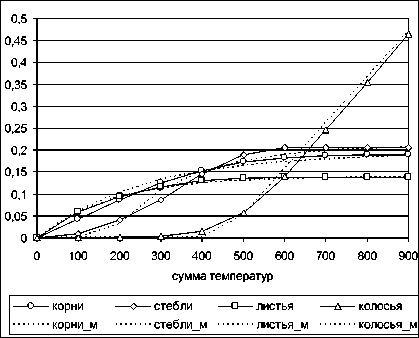
Рис. 6. Функции модели для ячменя, по рис. 5, см. п. 5

Для ячменя, как и для картофеля, по модели (рис. 6) легко различимы функции роста служебных органов и урожая (колосьев); для пшеницы получается несколько иной результат, – к функции роста урожая относится не только рост колосьев, но и стеблей (т. е. пшеница, кроме зерна, на урожай, как на результат интегрального роста биомассы, дает и солому), см. рис. 7.

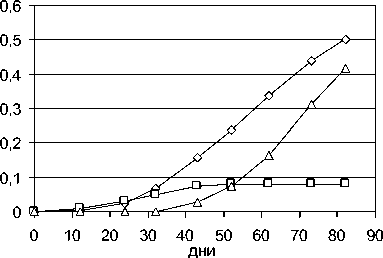
стебли     листья     колосья

Рис. 6. Приближенные функции роста для пшеницы, к итоговой биомассе, по проинтегрированными и перенормированным данным из [10]

Заключение

Таким образом, с использованием интегральных данных, приведенных к общей биомассе растения на конец роста, посредством стандартных средств теории автоматического управления (функций реакций основных передаточных звеньев на единичное воздействие), построены простые модели роста культурных растений, допускающие ясную качественную интерпретацию, и требующие дальнейшего определения количественных параметров.