Построение трендовой составляющей аддитивной модели долгосрочного прогнозирования объемов потребления электроэнергии оптового рынка электрической энергии и мощности России на примере объединенной энергосистемы Урала

На электроэнергетическом рынке плановые объемы потребления формируются на основе двусторонних договоров. В действительности фактические объемы электропотребления практически всегда отличаются от плановых. Отклонения от плановых показателей продаются на балансирующем рынке (БР), при этом системный оператор Единой энергетической системы России (СО) регулярно проводит дополнительные конкурентные отборы заявок поставщиков, с учетом текущего прогнозного потребления электроэнергии.

Причины возникновения отклонений различны и квалифицируются собственными или внешними инициативами. Собственная инициатива возникает по причине действий участника рынка (потребителя или поставщика), внешняя – в результате команд СО или аварии, приведшей к вынужденному изменению режима производства или потребления электроэнергии [1].

Для определения стоимости отклонений для различных видов инициатив используются расчетные формулы (срезки), рассчитываемые на каждый час суток для каждого узла расчетной модели. Срезки определяются как максимальные (минимальные) значения индикатора БР и цены рынка на «сутки вперед» (РСВ), тем самым стимулируя к более точному исполнению планового потребления и производства электроэнергии. На основе стоимости отклонений определяются предварительные требования и предварительные обязательства БР, разница между которыми формирует небаланс БР. Цены балансирующего рынка формируются на основании рыночных кривых спроса и предложения, при возникновении изменений спроса, если нужно большее или меньшее количество электроэнергии. Если фактическое электропотребление энергосистемой превысило план, то системный оператор поочередно рассматривает заявки генераторов, начиная с ближайшей справа от равновесной цены. Заявки генераторов присоединяются, пока не будет удовлетворена потребность покупателей в электроэнергии. Цена балансирующего рынка в данном случае будет равна точке пересечения необходимого покупателям объема с кривой предложения.

Если же возникла обратная ситуация и фактическое электропотребление энергосистемой оказалось ниже плана, то системный оператор поочередно снижает нагрузку электростанций, начиная с ближайшей слева от равновесной цены. Цена балансирующего рынка в данном случае будет определена по цене заявки генератора, чья ступень оказалась на пересечении с необходимым потребителям объемом.

Таким образом, в условиях работы Оптового рынка электрической энергии и мощности России задача долгосрочного прогнозирования основных параметров рынка электроэнергии является весьма актуальной и практически значимой [2]. Одновременно важна оценка прогнозных значений максимальной нагрузки и максимального потребления, базой для которой служит накопленная статистика по работе рынка.

Определимся со структурой аддитивной модели прогнозирования.

Временной ряд является совокупностью трех составляющих [3]:

– долговременной тенденции или тренда (Т);

– периодических колебаний (S);

– случайных колебаний (E).

Данные по объему потребления электроэнергии можно отнести к временному ряду, так как показатели объема потребления являются численными показателями, упорядоченными во времени и характеризующими уровни развития потребляемой электроэнергии в последовательные моменты времени. Пример временного ряда объема потребления электроэнергии по данным ОЭС Урала с 2009 по 2017 гг. представлен на рис. 1.

На рис. 1 видно наличие случайных и периодических колебаний, но наличие тренда необходимо доказать с помощью формальных методов.

Интерес для данного исследования представляет анализ не только временного ряда объема потребления электроэнергии, но и тарифа РСВ. График динамики тарифа РСВ представлен на рис. 2.

Основная задача эконометрического исследования временного ряда заключается в выявлении функционального или количественного выражения всех отдельных составляющих аддитивной модели [4, 5].

Графический анализ временного ряда объема потребления электроэнергии (см. рис. 1) свидетельствует о наличии сезонных колебаний, период

Объем потребления, МВт*ч

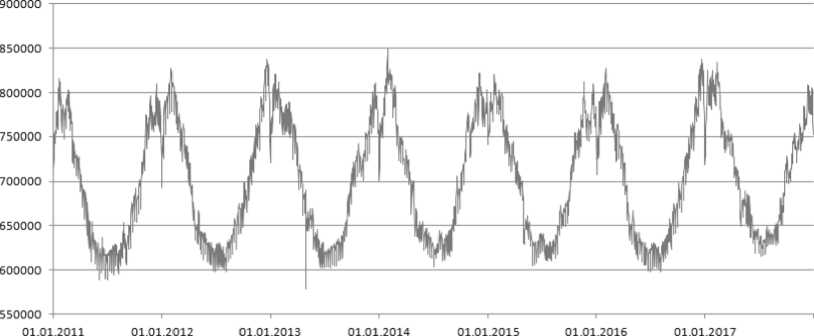
Рис. 1. Потребление электроэнергии ОЭС Урала в 2011 – 2017 гг.

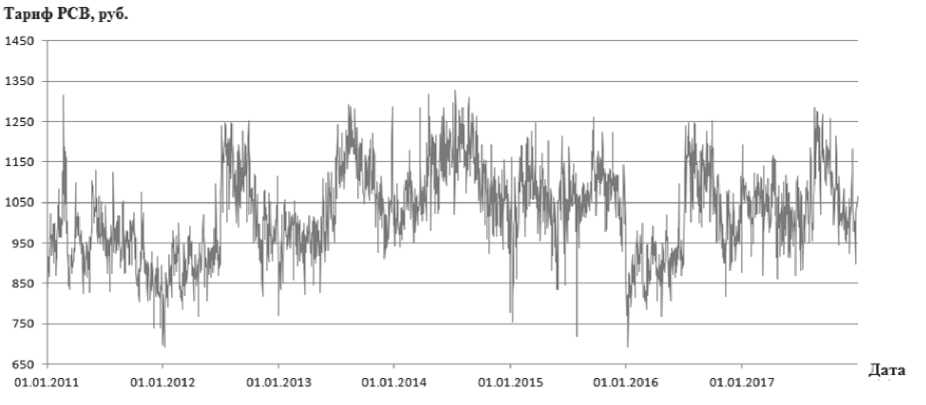
Рис. 2. Тариф рынка на сутки вперед по данным ОЭС Урала за 2011 – 2017 гг.

которых равен 1 году, наиболее существенные «всплески» в динамике ряда просматриваются при переходе из 4 квартала в 1, так как амплитуда периодических колебаний примерно постоянна, то для исследования выбираем аддитивную модель временного ряда:

Y = T + 5 + E . (1)

Определение функциональной формы тенденции временного ряда является важнейшей задачей анализа экономических процессов. Решение задачи моделирования тенденции начинается с определения ее наличия и предположений о характере тренда.

Решим задачу подбора методики для определения наличия тренда.

Одним из наиболее широко применимых методов диагностики наличия тенденции является метод сравнения средних, который применим для выявления монотонной тенденции временного ряда, который разбивается напополам, в результате чего получаются ряды: y ₁, y ₂,... y_{n 1} и

Уп1 +1, Уп1 + 2,-, Уп=п1 + n 2 с количеством уровней n и n2 . Отдельно для каждой части вычисляются средние уровней ( y1, y2) и выборочные дисперсии (s12,s22).

Далее рассчитывается значение критерия

Стьюдента по формуле [6]:

_т = | y i ^- y 2I

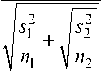
Нулевая гипотеза об отсутствии тенденции, т. е. о равенстве средних отвергается, если выполняется условие т >  t_{1 -a} m , где t_{1 -a} m - табличное значение t -критерия Стьюдента при уровне значимости а и числе степеней свободы m = п 1 + п ₂ - 2.

Суть второго метода (Фостера-Стюарта) заключается в том, что каждому уровню ряда yi , начиная со второго, ставится в соответствие два значения pi и qi по следующим критериям:

- p i = 1, если уровень y i меньше всех предыдущих уровней, иначе p i = 0 ;

- qi = 1, если уровень yi больше всех преды- дущих уровней, иначе qi = 0 .

Критерий принятия решений вычисляется по формуле [6]:

t_p > t_{1 -a} , _{n - 1}, где t _{1 -a} , _{n - 1} - табличное значение t -критерия Стьюдента при уровне значимости α и числе степеней свободы n – 1.

Согласно методу сравнения средних для временного ряда объема потребления электроэнергии т = 7,62 >  t ₀ 95 ₂₅₅₅ = 1,96 , а для ряда тарифа РСВ Т = 36,48 >  t 0,95,2555 = 1,96.

Согласно критерию Фостера-Стюарта для временного ряда объема потребления электроэнергии расчетное значение t_p = 50,537, что больше табличного значения t _{0 95 2556} = 1,96 , а для ряда тарифа РСВ t_p = 109,5, следовательно, наличие тенденции установлено обоими методами для обоих временных рядов.

Для определения типа тенденции возможно использование разных методик.

Прогнозирование стационарных временных рядов дает существенно лучшие результаты. Временной ряд называется стационарным, если уровни ряда приблизительно однородны и имеют вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени.

Для определения стационарности временного ряда используется тест Дики-Фуллера (тест на единичный корень), который основан на оценке параметра X = а 1 - 1 уравнения Y ( t ) = X • Y_t-1 + е _t . Выдвигаются 2 альтернативные гипотезы: H0: λ = 0; H1: λ<0. Для параметра λ рассчитывается значение t-статистики Стьюдента, если оно меньше нижнего порогового значения DF-статистики, то гипотезу о наличии единичного корня следует отклонить и принять альтернативную о стационарности процесса Y_t [1].

Самый распространенный метод приведения ряда к стационарному виду – это использование интеграции первого порядка, т. е. прогнозирование не самого ряда или процесса, а его изменения или прироста. Т. е. получаем ряд

ZL (t) = z (t) - z (t -1), где Z(t) – исходный временной ряд, а Z (t) – ряд прироста или разности соседних значений.

На практике иногда модель временного ряда получается более точной, если использовать инте- грацию второго порядка, т. е. делать не одно вы- t

p

n

S ⁽ P i ^- q)

= i =2 __________

ⁿ 2 ∑ ¹ i = 2 i

читание, а два, последовательно:

Z ( t ) = Z ( t ) - Z ( t - 1)

Z ( t ) = Z ( t ) - Z ( t - 1)

Аналогично методу сравнения средних выдвигается гипотеза об отсутствии тенденции, которая отвергается, если выполняется условие

В таком случае интегрировать, т. е. суммировать, придется дважды, чтобы спрогнозировать будущее значение искомого временного ряда. Брать порядок интеграции больше 2 раз неразум-

но, так как давно показана неэффективность подобных моделей.

Исследования на наличие тренда были проведены для рядов абсолютных изменений тарифа РСВ и объема потребления электроэнергии. Наличие тенденции в обоих временных рядах подтверждается методом Фостера-Стюарта, следовательно, с вероятностью 0,95 можно утверждать, что присутствует восходящая тенденция в рядах абсолютных приростов тарифа РСВ и объема потребления.

Исследуя последовательные разности уровней ряда y_t первого ( A y_t = y_t - y_{t - 1}), второго (A ² y_t = A y_t - A y_t - 1 ) и следующих порядков, можно сделать вывод о наличии тенденции, описываемой полиномиальной функцией от времени t [7, 8].

Если исходный временной ряд содержит тенденцию, а временной ряд последовательных разностей n -го порядка не содержит тенденцию, то можно сделать вывод, что тенденция задается полиномом порядка n:

y_t = а о + a i t + a 2 t ² +... + a n t n .               (5)

Для доказательства наличия экспоненциальной тенденции необходимо исследовать отношения последовательных уровней ряда (цепные коэффициенты роста) k_t = -y- , если исходный вре- y t - 1

менной ряд содержит тенденцию, а временной ряд коэффициентов роста не содержит тенденцию, то можно сделать вывод, что тенденция экспоненциально зависит от времени ( y_t = а 0 • а { ). Величина a ₁ в данном случае численно равна среднему коэффициенту роста уровня явления за единицу измерения временного параметра t.

Если наблюдается линейная зависимость между логарифмами уровней ряда ln y_t и соответствующих промежутков времени ln t , то рекомендуется использовать степенную функцию y_t = а 0 • / “ '

Было проведено исследование наличия тенденции для разностей уровней с 1 по 10 порядков, для каждого полученного ряда методом Фостера-Стюарта подтверждается наличие тенденции. Исследование разностей уровней более высоких порядков нецелесообразно, так как сложность вычислений по построенным моделям не оправдывается их точностью. Таким образом, исследование разностей уровней разных порядков не дает однозначного ответа об эффективном применении полиномиальных функций. Наличие степенной и экспоненциальной зависимостей тоже отвергаются, так как существует тенденция между цепными коэффициентами ряда, а коэффициент корреляции между натуральным логарифмом уровней ряда и натуральным логарифмом промежутков времени равен 0,244, что говорит об отсутствии корреляционной зависимости.

Аналогичные исследования были проведены отдельно для каждого года временного ряда объема потребления электроэнергии. Сводные результаты представлены в табл. 1.

Текущую экономическую ситуацию нельзя назвать стабильной, поэтому годовые экономические показатели могут существенно отличаться. Возникает вопрос, можно ли считать выборки наблюдения с 2011 по 2017 гг. единой выборкой или принципиально различными и уравнения регрессии для них должны строиться отдельно. Ответ на этот вопрос можно получить с помощью теста Чоу, согласно которому выдвигается гипотеза о том, что две выборки являются частями одной объединенной выборки.

Согласно тесту Чоу, нулевая гипотеза H ₀ о том, что две выборки являются частями одной объединенной выборки, отвергается при уровне значимости α, если выполняется условие: F =

( E ² - E 2 - E 2 ) • ( n - k i + k 2 )

( E \ + E 2 ) • ( k i + k 2 - k )

> F a ; k i + k 2 - k ; n - k i + k 2 ⁽⁶⁾

где E2 – сумма квадратов остатков объединенной выборки; E12 – сумма квадратов остатков первой выборки; E22 – сумма квадратов остатков второй выборки; k1 – количество объясняющих перемен- ных первой выборки; k2 – количество объясняющих переменных второй выборки; k – количество объясняющих переменных объединенной выборки; Fa;k1 + k2 -k; n-k1 + k2 — квантиль Фишера при заданном уровне значимости a и числом степеней свободы k1 + k2 - k и n - k1 + k2; n - количество наблюдений в объединенной выборке [9].

Результаты теста Чоу для линейных парных регрессий двух выборок подтверждают гипотезу H ₀ . Следовательно, весь период данных потребления и тарифа РСВ с 2011 по 2017 гг. можно рассматривать как единую совокупность. Исследование отдельных периодов этой совокупности не даст искаженных представлений о поведении всей совокупности в целом.

Анализируя полученные результаты, можно сделать следующие выводы:

Таблица 1

Показатели критерия Фостера-Стюарта для разностей уровней с 0 по 6 порядков

Порядок	2011	2012	2013	2014	2015	2016	2017
0	6,48	22,67	16,19	12,95	6,48	6,48	29,14
1	3,24	16,18	12,95	6,47	19,42	9,71	3,24
2	6,47	12,94	6,47	12,94	3,24	6,47	6,47
3	9,70	3,23	3,23	3,23	9,70	6,47	12,93
4	6,47	6,47	0	16,17	3,23	12,94	0
5	3,24	6,47	0	6,47	0	12,95	3,24
6	3,24	3,24	9,71	19,42	6,47	0	16,18

• 3 . Для 2015 и 2017 гг. наблюдается полиномиальная зависимость 5 и 6 порядков, соответственно.

Хотя использование полиномов высоких порядков может привести к повышению точности модели, но их построение и вычисления по ним являются трудоемким процессом. Так как в исследуемом временном ряду наблюдается сезонность, а наличие тенденции установлено, то целесообразно построить уравнения каждой компоненты аддитивной модели в отдельности. Уравнение тенденции получаем с помощью метода скользящего среднего. Цель сглаживания временного ряда по методу скользящего среднего заключается в получении ряда с меньшим разбросом уровней.

Сам метод заключается в замене исходных уровней ряда y_t сглаженными значениями y ' _t , которые получаются как среднее значение g уровней исходного ряда, симметрично окружающих значение y_t . Было проведено сглаживание временного ряда объема потребления электроэнергии для различных интервалов сглаживания:

• –    недельный, g = 7;

• –    месячный, g = 30;

• –    годовой, g = 365.

Временной ряд, полностью не подверженный колебаниям, получился для интервала сглаживания, равного 365, т. е. с периодом в 1 год. Результаты сглаживания представлены на рис. 3.

Были построены различные модели, описывающие полученный сглаженный временной ряд, сводные результаты представлены в табл. 2.

Согласно результатов табл. 2 наибольшую эффективность показывает модель полинома второго порядка, так как имеет наибольший коэффициент детерминации и наименьшую среднюю ошибку аппроксимации, т. е. наилучшим образом описывает исходные данные. Данную модель рекомендуется применять как трендовую составляющую аддитивной модели временного ряда объема потребления электрической энергии.

Решена задача построения трендовой составляющей аддитивной модели долгосрочного прогнозирования рынка электрической энергии и мощности России. Рассчитаны показатели и критерии, доказывающие эффективность и адекватность полученной модели. На основе данных объема по- требления электроэнергии ОЭС Урала за 2011– 2017 гг., взятых с официального сайта Системного оператора Единой энергетической системы России, тестом Чоу доказано, что рассматриваемый временной промежуток можно считать единой совокупностью. Установлено наличие трендовой составляющей. Ошибка аппроксимации для модели тренда в виде полинома второго порядка составила 0,33 %. Совокупность данных фактов говорит о том, что разработанная модель является достоверной для долгосрочного планирования объемов потребления рынка электрической энергии и мощности России, и ее использование позволит повысить энергоэффективность производства промышленным предприятиям при работе на Оптовом рынке электрической энергии и мощности.