Поведение полиномов Гронуолла на границе области суммируемости

В работе [1] показано, что если метод (bm,n) суммирует ^k_0zk к 1/(1 - z) в некоторой об- k ласти D, то можно описать область Df, в которой этот метод будет суммировать ^ akzk к k=0

f ( z ) • Поэтому изучение С- областей метода суммирования достаточно провести для геометриче-

Е”  к к=0 z

•

Гронуолл в работе [4] описал широкий класс методов суммирования расходящихся рядов. Метод Гронуолла [ F ( w );1(1 - w ) ] задается отображающей функцией F ( w ) = ^ k = 1 C k w^k ( c * 0) и весовой функцией 1/(1 - w ), и элементы его матрицы определяются по формулам

F 1 г (1 - F ( w )) F n ( w ) , .

cF п = —Ф  ---- dw ( m , n >  0), ^m ’ n 2 n * (1 - w ) w^{m + 1}

где интегрирование ведется по у - простому достаточно малому контуру вокруг начала координат. На отображающую функцию F ( w ) в работе [1] накладываются три условия: 1) F ( w ) анали-

Краткие сообщения

тична в замкнутом единичном круге K , исключая, может быть, точку w = 1, и однолистна в K ; 2) F ( w ) непрерывна в K , F (0) = 0, F (1) = 1, F ( K ) с K ; 3) ряд Тейлора F ( w ) абсолютно сходится при w = 1.

Определение. Полином P m ( z ) = ^ ^ = 0 c F , _n ( ^ k = 0 z k ) будем называть m -м полиномом Грону-олла метода [ F ( w ); 1/(1 - w ) ] .

Из условия F (0) = 0 следует, что c m , _n = 0 при n >  m , поэтому степень m -го полинома Гро-нуолла не превосходит m . Область T ( F ), ограниченную кусочно-гладкой кривой т (F ) = { z : z = [ F ( e^{l x} )] ^{- 1} , x e [0 ; 2 n ]} назовем областью суммируемости метода [ F ( w );1/(1 - w ) ] .

^

Как доказано в работах [2] и [3] метод [ F ( w );1/(1 - w ) ] суммирует ряд ^ z^k к 1 / (1 - z ) в области к = 0

T ( F ). Вне этой области последовательность P m ( z ) расходится. Условие F ( K ) с K означает, что область суммируемости метода [ F ( w );1/(1 - w ) ] включает область сходимости степенного

Z “ к к = 0 ^z .

В работе [2] рассматривается скорость сходимости полиномов Гронуолла в случае аналитической отображающей функции внутри области T ( F ).

Легко видеть, что последовательность Pm (z) не обязана сходится к 1/(1 - z) на границе области T(F). Для F(w) = w, например, последовательность Pw (z) = ^yzm не сходится к у1- ни для m         1-z                       1-z какого z, лежащего на границе области T(F), равной единичному кругу. Тем не менее последо вательность {Pm (z)} ограничена для каждого z Ф1. Аналогичный факт имеет место и в общем случае.

Теорема . Если отображающая функция F ( w ) имеет ограниченное изменение на единичной окружности и ее производная не равна 0 на единичной окружности, то для каждого z e т ( F ) \ {1} последовательность { P m ( z )} ограничена.

Доказательство. В работе [1] показано, что

PF = J1 X    (1 - F (w)) dw m 1 - z 2ni -^ (1 - zF(w))(1 - w) wm+1 .

Поэтому достаточно для оценки полинома P m ( z ) оценить интеграл

1 г     (1 - F ( w )) dw

2ni ® (1 - zF(w))(1 - w) wm+1 , т.е. коэффициент при wm в разложении в степенной ряд функции (|zF^w^-w). Так как z e т(F) \ {1}, то z = 1/F(w0) для некоторого w0 = e“0, где x0 e (0; 2п). Рассмотрим функцию

(1 - F ( w ))( w _n - w ) ------------⁰-----, если w Ф w<

1 - zF ( w )                 ⁽

(1 - F ( w )) F ( w ₀)

-------------—, если w = w _n.

F / w e)              ⁰

Докажем, что степенной ряд функции ^(w) абсолютно сходится при w = 1. Выберем такое число в > 0 , что x0 e (Р,2л - Д). Так как функция F(w) имеет ограниченное изменение на единичной окружности, то и Re (^(eix)), и Im (^(eix)) также имеют ограниченное изменение на отрезках [0, Д] и [2п - Д, 2.П] как дробно-рациональные функции от функций с ограниченным из-

Матвеева Л.В.

Поведение полиномов Гронуолла на границе области суммируемости менением. Так как (1 - zF(w))w=w0 =-zF'(w0) * 0, то функция ^.Fww) имеет в w0 простой полюс, и функция ф(w) аналитична в w0 . Отсюда вытекает, что Re (ф(eix)) и Im (ф(eix)) имеют ограниченное изменение на отрезке [в,2п - в]. Следовательно, Re (ф( eix)) и Im (ф( eix)) имеют ограниченное изменение на всем отрезке [0,2п] и по теореме Харди-Литлвуда степенной ряд ф(w) абсолютно сходится при w = 1. Представим функцию TpzFFywj-w) в виде произведения ф(w) на

~              ~

7---—г. Перемножим степенные ряды -,—¹—г = — > , „ w и -¹- = > w :

( w g - w )(1 - w )      '                              '       ( w ₀ - w ) w ₀ Z—tk = 0         1 - w n—in = 0

( w ₀ - w )(1 - w )

w ₀

I

^

= 0

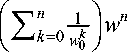
1 ^—1 ^

^^ n = 0 w ₀    ⁿ

1L

... n + 1 w ₀

^{1 - w} 0

wn

Перемножим степенные ряды

ф ^{( w} ) = I n = 0 b n w n

1              1     ^       wn+1   и и---------= — I --— wn .

( w ₀ - w )(1 - w )   w ₀    ^{n 0} 1 - w ₀

Получим

ф ^{( w} )

( w ₀ - w )(1 - w )

w ₀

-

E^ [ m i   m=01 ^^ k=0 k ^^

m

bk

■ k = 0 w m ^{+ 1 - k}

wm

Z ^

k = 0 l b k I = C . Тогда

• ¹    d)     ^{(1 -} F ^{( w}))d^w     = ¹ fV ^m b - V m    ^bk ) <  2 c

2 n i ; (1 - zF ( w ))(1 - w ) w^{m + 1}     w 0 - 1 1^{1 k} = ⁰ k ^{1 k} = ⁰ w m ^{+ 1 - k} J - | w 0 - 11"

Таким образом, p F ( z )| < |j- z | + |ji zz | i wC i. И правая часть выражения не зависит от m . Теорема доказана.