Повышение эффективности передачи и распределения электрической энергии в условиях Севера и Арктики

Электроснабжение труднодоступных территорий северо-востока России, в частности Республики Саха (Якутия), осуществляется в основном от секций шин 6 (10) кВ понижающих подстанций, подводящих электрическую энергию от дизельных электрических станций (ДЭС) к районным центрам муниципальных образований (рис. 1) [1]. Данные электропередачи имеют из-за природноклиматических особенностей региона большую протяженность воздушных ли- ний электропередачи (ВЛ), характеризуются перегрузкой трансформаторных подстанций 10/0,4 кВ внутри районных центров, недогрузкой в относительно небольших сельских поселениях, а так же несоответствием в определенных отрезках сечения проводов передающейся мощности, что приводит к увеличенным потерям активной мощности в цепочке «секция шин 10 кВ подстанции» - «конечный потребитель», слабой надежностью электропередачи и не эффективной работой ДЭС [2].

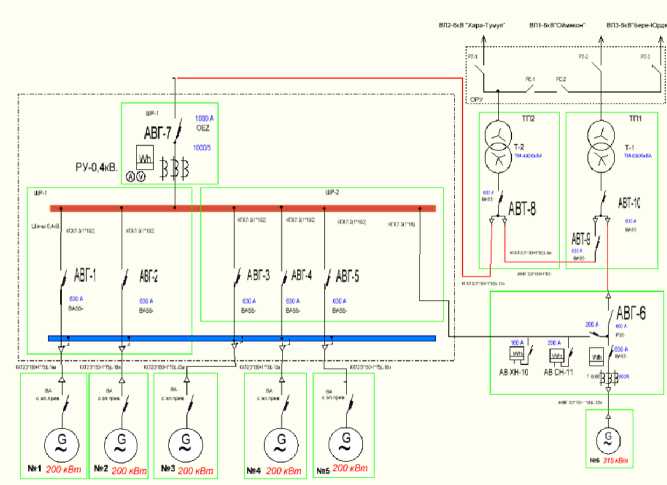
Рис. 1. Схема выдачи электрической энергии

Для решения данной проблемы предлагается использование оптимизационных методов, основанных на принципах математического программирования, позволяющее найти экстремальные значения целевой функции, которая является формализованным математическим описанием или моделью, раскрывающей протекающие в указанных распределительных сетях процессы.

Целевая функция в данном случае представляет собой функцию для которой требуются определить экстремумы в зависимости от критериев оптимальности, таких как: минимум потерь активной мощности в электрических сетях, оптимальное расположение центров питания, подбор оптимального сечения проводника, подбор оптимальной трассы для питания центров питания или конечных потребителей и т.д. В единой целевой функции возможно применения в качестве критерия оптимальности минимального значения суммарных приведенных затрат, но для упрощения вычислительной нагрузки предлагается разбить имеющуюся задачу по оптимальному электроснабжению сельских поселений на несколько блоков, которые буду взаимодействовать между собой с помощью исходных и выходных данных.

Основные параметры, которые сведены в отдельные расчетные блоки:

• -    построение картограммы и определение условного центра электрических нагрузок;

• -    выбор места расположения распределительных пунктов и трансформаторных подстанций;

• -    схемы питающих и распределительных сетей;

• -    выбор сечений п роводников на высокой и низкой классах напряжения.

Для сопоставления физических параметров, например, геометрических размеров участка электроснабжения, длин линий электропередачи, определения фактического места установки центров питания или введения дополнительных ограничений по размещению объектов электроэнергетической инфраструктуры, с расчетными параметрами, требуется совместить генеральный план с координатной плоско- стью и обозначить координаты, размещаемых объектов по оси абсцисс и ординат в о.е.

Далее идет ввод исходных данных.

Пример оптимального проектирования схемы электроснабжения показан в работе [2].

Производится проектирование схемы электроснабжения сельского поселения. Определены требуемая мощность конечных потребителей и располагаемый резерв мощности близлежащих трансформаторных подстанций. Известны также расстояния от питаемых объектов до каждой трансформаторной подстанции. Требуется определить оптимальную с точки зрения минимума приведенных затрат схему электроснабжения предлагаемого района.

Приведенные годовые затраты на сооружение и эксплуатацию электрической сети определяются по выражению:

З_пр = РнК + Сэ , руб, где р н — нормативный коэффициент капитальных вложений; К - капитальные вложения; С э - стоимость потерь электроэнергии в проводах ЛЭП.

Величина капитальных вложений на сооружение ЛЭП зависит от ее сечения и длины:

К = (a + Ь х S) х l , руб, где a,b - расчетные коэффициенты; S,l - сечение и длина ЛЭП соответственно.

Стоимость потерь электрической энергии в проводах ЛЭП определяется законом Джоуля-Ленца:

С_э = З х 1 ² х R х Ц х t , где I, R - ток в фазе линии и ее активное сопротивление; Ц - отпускная цена кВт^ч электрической энергии; t - число часов работы линии в год.

Активное сопротивление линии можно определить по выражению

l

R = р — , где р - удельное сопротивле ние материала провода. Сечения проводников в сетях высокого напряжения определяются по экономической плотности тока:

Для n участков электрической сети суммарные приведенные затраты определятся выражением:

mn     mn

З пр = ZZ k i ^x lu + ZZ ^k 2 ^x kj ^x I и , где i = 1 j = 1                  i = 1 j = 1

I ij – ток, потребляемый j-м потребителем с i-й подстанции; l ij – расстояние от j-го потребителя до i-й подстанции; k 1 , k 2 – постоянные коэффициенты.

Для достижения минимальных приве- денных затрат достаточно минимизировать второй член уравнения, при этом значение коэффициента k2 можно не учитывать. С учетом того, что ток в линии прямо пропорционален передаваемой по ней мощности, получим выражение целевой функции решаемой задачи:

mn

Z = ZZ P ,j X I, j

^ min.

Требуется найти минимум целевой функции при следующих ограничениях:

• 1.    Суммарная мощность, потребляемая всеми потребителями с одной подстанции, должна быть равна располагаемой мощности подстанции

• 2.    Суммарная мощность, передаваемая всеми подстанциями одному потребителю, должна быть равна требуемой мощности этого объекта

• 3.    Величина мощности, передаваемой по линии, должна быть положительной.

Перед решением задачи необходимо проверить баланс располагаемой и требуемой мощности и при необходимости привести задачу к сбалансированной.