Представители множеств в диагностике
Автор: Мазуров вЛ.Д., Смирнов А.И.
Журнал: Вестник экономики, управления и права @vestnik-urep
Рубрика: Математика
Статья в выпуске: 2 (31), 2015 года.
Бесплатный доступ
Представитель множества - произвольный элемент этого множества. Это понятие применяется к решению задачи факторного анализа. Данный метод связан с кластерным анализом. Демонстрируется применение предлагаемых идей к комитетным конструкциям и восстановлению трехмерных изображений по их плоских проекциям.
Представитель множество кластер, факторный анализ анализ изображений
Короткий адрес: https://sciup.org/14214680
IDR: 14214680 | УДК: 519.95+519.863
Текст научной статьи Представители множеств в диагностике
Представитель множества – любой его элемент. Система представителей набора множеств – любое множество, имеющее непустое пересечение с каждым множеством этого набора. Понятие системы представителей является частным случаем понятия комитетной конструкции [1]. В случае бесконечных множеств проблема представителей связана с противоречиями – это известная аксиома выбора. Далее мы будем рассматривать только конечные множества. Проблема нахождения минимальной системы представителей и важна, и трудна. Системы различных представителей наборов множеств изучались ещё с 1935 года Ф. Холлом (Hall P.) [2], затем П .Халмошем (Halmos P.R.) [3] в 1950 году, А. Гофманом (Hoffman A.J.) и Г. Куном (Kuhn H.W.) [4] – в 1955 году. С 1998 года – А.М. Райгородским [6], Ю.И. Журавлевым [7], Ю.А. Флеровым [8] в ряде работ по комбинаторной оптимизации.
Комитетные конструкции примыкают к этому направлению. Для числа p (0 < p < 1) p -комитетом системы множеств называется множество C такое, что его пересечение с каждым множеством системы содержит более, чем p -ю часть множества C . Такие конструкции изучались Вл.Д. Мазуровым [1; 8] с 1965 года, М.Ю. Хачаем [8; 9] с 1995 года. Идея комитетных конструкций состоит в том, чтобы вместо одного решающего правила искать коллектив решающих правил, этот коллектив вырабатывает коллективное решение в силу процедуры, обрабатывающей индивидуальные решения членов коллектива.
Так, например, комитет системы неравенств – это такой набор элементов, что каждому неравенству удовлетворяет большинство элементов этого набора.
Комитетные конструкции – некоторый класс обобщений понятия решения для задач, которые могут быть как совместными, так и несовместными. Это класс дискретных аппроксимаций для противоречивых задач, их можно также соотнести с т.н. раз- мытыми решениями. Метод комитетов в настоящее время определяет одно из направлений анализа и решения задач эффективного выбора вариантов, оптимизации, диагностики и классификации.
В процессе эксплуатации метода комитетов выявились такие его важные для прикладных задач свойства, как эвристичность, интерпретируемость, гибкость – возможность дообучения и перенастройки, возможность использования наиболее естественного класса функций – кусочно-аффинных функций.
Другая сторона вопроса о комитетных конструкциях связана с понятием коалиций при выработке коллективных решений, при этом ситуации резко различаются в случае коллективных предпочтений (здесь много подводных камней) и в случае правил коллективной классификации, в этом случае процедуры можно строго обосновать и они имеют более широкие возможности.
При решении задач диагностики и прогнозирования предприятий часто используются веса факторов, которые даются экспертами, а далее проводится голосование мнений экспертов. Однако такие процедуры могут быть некорректными, и существует аппарат построения корректных процедур.
Нами показано, что при сведении задачи к классификационной можно строить коллективы экспертов (комитеты), корректно решающие задачу диагностики. Метод комитетов здесь позволил получить точные результаты и обоснованные процедуры обучения, которые позволяют решать широкий класс задач, сводимых к разделению конечных множеств с единственным требованием непустоты их пересечения.
В наших работах мы выдвинули прецедентно-классификационный принцип, применение которого позволяет избежать противоречий выбора. А именно, предлагается следующая схема: задача принятия решений сводится к задаче классификации или к обучению распознаванию на основе прецедентов. Попу- лярное изложение этих методов содержится, например, в работе [10].
Далее задача классификации сводится к системе линейных неравенств. которая может быть и несовместной. Для этой системы находится комитетное решение, которому соответствует корректное решающее правило диагностики.
При попытке подбора модели фиксированного класса для описания материала наблюдений может возникнуть противоречие, если упомянутый класс моделей слишком узок. Это противоречие выразится в том, что задача идентификации модели, имеющая вид системы соотношений, связывающих параметры модели, не будет иметь решения.
В этом случае можно либо расширять класс используемых моделей, включая в него более сложные, либо использовать «коллективы» моделей. В данной работе реализуется второй путь, причём используются конструкции максимальных совместных и минимальных несовместных подсистем, а также понятие p -комитета.
Напомним определения этих понятий [1] для случая системы соотношений вида x e Dj (Vj e J) (1)
где Dj – некоторые заданные множеств а (например, Dj может представлять собой множество всех решений какого-либо неравенства).
Определение 1. Максимальной совместной подсистемой системы (1) называется такая совместная подсистема x e Dj (Vj e S), где S c J, что для любого i e J \ S система x e D j (Vj e S U {i})
несовместна.
Определение 2. Минимальной несовместной подсистемой системы (2) называется такая несовместная подсистема x e D j (V j e T ), где T c J, что для любого i e T система x e D (Vj e T \{i})
совместна.
Определение 3. Пусть 0 < p < 1 . Конечное множество K называется p -комитетом системы (1), если
IK n Dj| > p|K| (Vj e J), где A означает число элементов множества A .
Перечисленные конструкции применяются в распознавании образов и в математической статистике. Другие приложения связаны с задачами Борсука [11] о разбиении множества на части меньшего диаметра, Эрдёша-Хадвигера о раскрасках [12], Грюнбаума о покрытии множеств шарами [13]. Имеются также приложения в геометрии чисел.
В геометрии чисел изучаются свойства чисел с помощью геометрических методов. Наряду с Г. Минковским основателем этой теории ее классиками также являются Дж. Фаркаш (Farkas J.) [14], Г.Ф. Вороной [15], С.Н. Черников [16], И.И. Ерёмин [17].
В частности, в геометрии чисел доказан следующий факт: если на плоскости взять любой симметричный прямоугольник площадью более четырёх, то в нём обязательно окажется точка с целыми координатами и хотя бы одна из координат – ненулевая.
Теорема Минковского-Фаркаша [17] даёт условия того, что некоторое линейное неравенство является следствием системы линейных неравенств.
Интересно, что теория размерностей Вапника-Червоненкиса [18] также связана с упомянутыми конструкциями. Эта размерность для совокупности M областей из X есть мощность максимального множества A из X , которое дробится областями из M , т.е. проекция M на A – это все подмножества множества A .
В качестве простого приложения упомянем задачу о формировании группы экспертов, покрывающей компетенциями некоторую проблемную область. Важны также за- дачи кластеризации конечных множеств – соответствующие методы применяются в экономике. Ещё один интересный пример приложений – поиск факторов в задачах анализа сигналов.
По замечанию нобелевского лауреата Даниэля Канемана [19], американского психолога, восприятие информации основано на субъективном опыте, но согласованный совместный поиск учёных направлен на объективное восприятие данных. В этом случае важны математические методы обработки знаний.
Здесь предлагается новая процедура латентного факторного анализа, зависящая от некоторого заранее выбранного класса функций F е {Rm ^ R }. Подобный метод использовался в одном медицинском исследовании [20] факторов риска заболеваний – при сотрудничестве с д.м.н. Е.Р. Лебедевой и магистром математики Д.В. Гилёвым. При этом разработан новый метод факторного анализа. Этот метод использует нахождение минимальных по включению несовместных и максимальных по включению совместных подсистем системы f (x) > 0 (x е L, f е L‘).
Здесь L – действительное линейное пространство, L - сопряжённое пространство непрерывных функций над L . Названные подсистемы используются в определении дискриминантных функций и кластеров при распознавании образов.
Конкретизируем постановку задачи в частном случае. Предположим, что получен материал наблюдений в виде таблицы объект\ признак:
A = a 1 , a
,
am = [ a 1 , a 2 ,..., a n ] .
Здесь вектор-строка ai – описание i -го объекта, aj – вектор-столбец значений j -го признака на объектах.
Используем функции f е F , где функция f , первоначально неизвестная, определяет в результате анализа форму кластера. Запишем систему ограничений:
f ( a j> 0 ( j е J , f е G ).
Это система неравенств относительно неизвестной функции f . Если система совместна, то считаем, что имеется только одна латентная переменная – она является комбинацией совокупности всех признаков. Однако, как правило, эта система несовместна. В таком случае выбираем решения максимальных по включению совместных подсистем этой системы – от каждой подсистемы по одному решению.
В итоге получаем набор f 1 ,..., f q . Для fk кластер переменных имеет вид G k = { j е J : f k ( a , .) > 0) } . Тогда соответствующий латентный фактор – это комбинация признаков, входящих в Gk .
Класс F выбирается в соответствии с содержательным смыслом кластеров. Как правило, используется класс квадратичных функций f ( x ) = xTQx + b , где Q - матрица.
Что касается других постановок задачи анализа изображений, то мы рассматривали [21] также неоднозначную интерпретацию n -мерных сцен как проекций «прозрачных» полиэдров в пространство меньшей размерности. При этом использовался аппарат линейного программирования. В данной работе применяется метод максимальных по включению совместных подсистем (МСП) для восстановления трехмерной структуры многогранника по его известным ортогональным проекциям.
В классической постановке этой задачи предполагается наличие нескольких ракурсов изображения, позволяющих разрабатывать алгоритмы на основе хорошо апробированных проективных методов, таких, как например, алгоритм восстановления по стереопаре (Standard and Wide-base Stereo) и других (см. обзор [22]). Но в настоящее время внимание исследователей смещается в область восстановления трехмерных сцен по одному изображению [23]. Интересен в связи с этим проект Корнуэльского университета (Cornell University) «Make3D», начавшийся в Стэндфордском университете и также имеющий целью решение пока еще не ставшей типичной задачи восстановления трехмерной модели сцены всего по одному фотоснимку. Этот проект показал, что значительный объем информации содержится в так называемых монокулярных признаках (monocular cues) самого изображения, которые до этого зачастую игнорировались. Для понимания механизмов формирования видимых образов особый интерес представляет анализ неоднозначных изображений, которые допускают две или более интерпретации (так называемые трансформирующиеся или обращающиеся изображения). В данной работе рассматривается одна из разновидностей этой задачи задача интерпретации плоских проекций трехмерных объектов – «прозрачных многогранников», заданных их скелетами. Эта задача важна не только в прикладном аспекте, но и с точки зрения понимания механизмов восприятия и интерпретации изображений человеческим мозгом. Особенно интересен аспект восприятия человеком так называемых двойственных и противоречивых отображений, эта задача интенсивно исследуется в последние годы философами, психологами и математиками [24].
Одним из самых простых и самых исследованных изображений такого рода является так называемый куб Неккера [25] – контурное изображение, соответствующее параллельной проекции вершин и ребер куба на плоскость. Это изображение и две его возможные пространственные интерпретации приведены на рис. 1 :
При достаточно длительном наблюдении эта фигура как бы спонтанно (самопроизвольно) «переворачивается»: одна объемная проекция сменяется другой. По-видимому, в данном случае обе интерпретации равноправны и мозг «пробует» каждую из этих гипотез поочередно, не имея оснований выбрать окончательно одну из них – полностью отсутствует контекстная информация (отсутствует перспектива - нет разницы в размерах граней), помогающая принять решение в распознавании обычных зрительных образов.
Закономерности динамики восприятия таких неоднозначных фигур подробно анализировались, в частности Дж. Кальоти [26], показавшим, что во многих отношениях они сходны с явлениями самоорганизации в диссипативных структурах за порогом неустойчивого, критического состояния. Особенностью этих процессов является динамическое чередование (инверсия) двух стационарных состояний, в которых находится система.
Куб Неккера является представителем т.н. класса «каркасных моделей», содержащими только вершины и ребра объекта.
Идея использования максимальных непротиворечивых подсистем приводит к новому подходу к решению задачи трехмерной интерпретации плоских изображений на основе поиска максимальных (по включению) совместных подсистем некоторой несовместной системы линейных неравенств. В качестве класса трехмерных объектов при этом используется класс вы-
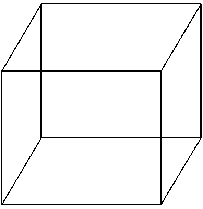
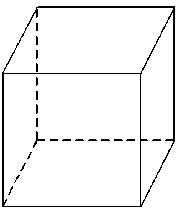
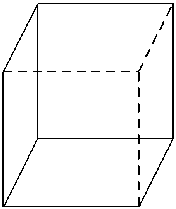
Рис. 1. Куб Неккера и его возможные пространственные интерпретации пуклых многогранников, а неравенства упомянутой несовместная система ограничений отражают требования видимости граней этого многогранника.
В наших работах [21, 27] демонстрируется новый подход к решению задачи трехмерной интерпретации плоских изображений на основе поиска максимальных (по включению) совместных подсистем некоторой несовместной системы линейных неравенств. В качестве класса трехмерных объектов при этом используется класс выпуклых многогранников, а неравенства упомянутой несовместной системы ограничений отражают требования «видимости» граней этого многогранника. При этом понятие «видимости» в работе [21] строго формализовано и корректность его определения доказана соответствующими утверждениями.
Список литературы Представители множеств в диагностике
- Мазуров Вл.Д. Метод комитетов в задачах оптимизации и классификации. М.: Наука, 1990.
- Hall P. On Representatives of Subsets. J. London Math. Soc. 1935. 10 (1). P. 26-30.
- Halmos P.R., Vaughan H.E. The marriage problem // American Journal of Mathematics. 1950. №72. PP. 214-215.
- Hoffman A.J., Kuhn H.W. On Systems of distinct representative // Linear inequalities and related systems. Annals of mathematics studies. 1956. No. 38. P. 199 - 206.
- Райгородский А.М. Системы общих представителей. М.: Изд-во МФТИ - МЦМНО, 2009.
- Журавлёв Ю.И. Избранные научные труды. М.: Магистр, 1998.
- Журавлёв Ю.И., Флёров Ю.А., Вялый М.Н. Дискретный анализ. Основы высшей алгебры. М.: МЗ-Пресс, 2006.
- Мазуров Вл.Д., Хачай М.Ю. Бустинг и полиномиальная аппроксимируемость задачи о минимальном аффинном разделяющем комитете // Труды Института математики и механики. 2013. Т. 19. № 2. С. 231 - 237.
- Хачай М.Ю. О вычислительной сложности задачи о минимальном комитете и смежных задач // Докл. РАН. 2006. Т. 406. № 6. С.742-745.
- Мазуров Вл.Д., Смирнов А.И. Методы распознавания образов в интеллектуальных информационных системах // Вестник Уральского института экономики, управления и права. 2008. №2(3). С. 122-131.
- Райгородский А.М. Проблема Борсука. М.: Изд-во Московского центра непрерывного математического образования, 2006.
- Райгородский А.М. Проблема Эрдеша-Хадвигера и хроматические числа конечных геометрических графов // Матем. сб., 2005. Т. 196. № 1. С.123-156.
- Райгородский А.М. Проблемы Борсука и Грюнбаума для решетчатых многогранников // Изв. РАН. Сер. матем. 2000. Т. 69. Вып. 3. С. 81-108.
- Farkas J. Ьber die Theorie der Einfachen Ungleichungen // Journal fьr die Reine und Angewandte Mathematik. 1902. No. 124 (124). P. 1 - 27.
- Вороной Д.Ф. Исследования многогранников. - Журнал чистой и прикладной математики. 1908. №134. С.198 - 207.
- Черников С.Н. Линейные неравенства. М.: Наука, 1968.
- Еремин И.И. Системы линейных неравенств и линейная оптимизация. Екатеринбург: Изд-во УрО РАН, 2007.
- Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М.: Наука, 1974.
- Канеман Д. Думай медленно… Решай быстро. М.: АСТ, 2013.
- Гилев Д.В., Лебедева Е.Р., Мазуров Вл.Д. Анализ факторов возникновения голов- ной боли (сдано в печать в Уральский медицинский журнал).
- Мазуров Вл.Д., Смирнов А.И. Интерпретация противоречивых изображений на основе систем линейных неравенств // Труды Института математики и механики УрО РАН. 2012. Т. 18. № 3. С. 144 - 154.
- Юрин Д.В. Современные концепции восстановления трехмерных сцен по набору цифровых изображений: наполнение систем виртуальной реальности // Трехмерная визуализация научной, технической и социальной реальности. Кластерные технологии моделирования. Ижевск: УдГУ, 2009. Т. 1. С. 96-100.
- Hartley R., Zisserman A. Multiple view geometry in computer vision. Cambridge: Cambridge University Press, 2004. 672 p.
- Евин И.А. Синергетика мозга. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2005.
- Грегори П. Разумный глаз. - М.: Мир, 1972.
- Кальоти Дж. От восприятия к мысли. М.: Мир, 1998.
- Мазуров Вл.Д., Смирнов А.И. Противоречия и классификация // Вестник Уральского института экономики, управления и права. 2011, №1(14). С. 86-94.


