Представление трех безразмерных геометрических характеристик пищевых пористых систем в форме статистических функций

Исключительное многообразие материалов, имеющих поровую структуру, объясняет использование почти в любом производстве процессов, связанных с тепло-и массо-обменом в этих сложных системах. Это сушка, влагона-полнение и любые другие фильтрационные процессы в пищевых, медицинских, химических, нефте- и газодобывающих технологиях, в агросекторе, сохранении и дренировании грунтовых вод и др., где перерабатывается дисперсная среда или твердые пористые материалы [1–7].

Реальные пористые среды имеют сложную систему порового пространства, которую

невозможно полностью формализовать с одновременным учетом всех ее особенностей. Поэтому для расчетов фильтрационных задач с определением скоростей движения фильтрата, эффективности промывки, растворения, сушки осадка или любого пористого материала используют экспериментальные геометрические параметры пористых материалов. В их числе три базовых безразмерных геометрических параметра в виде коэффициентов прерывистости, просветности и пористости [6]. Эти коэффициенты относятся ко всей совокупности полиразмерной поровой структуры и потому являются интегральными осредненным физическими параметрами, характеризующими пористую систему в целом [3, 6].

Исследования геометрии пористого пространства имеют долгую историю. Много публикаций со статистическими исследованиями появлялось в последние два десятилетия, о чем свидетельствуют объемные обзоры, например, в [8, 9]. В публикациях направленность исследований с учетом полиразмерной микроструктуры порового пространства связана со стыковкой статистических функций случайного распределения размеров пор с экспериментальными результатами, например, с гистограммами, и определением на этой основе интегральных характеристик порового пространства [10]. Ими нельзя оценивать вклад пор отдельных размеров или размерных групп. При этом понятно, что поток в мелких порах движется медленнее по сравнению с потоком в крупных, и в реализуемом процессе проявляется неоднородность, например, в условиях промывки, сушки, экстракции, вытеснения. Отсюда следует актуальность разработки таких геометрических безразмерных коэффициентов, в которых отражались бы функции статистического распределения пор по размерам в полиразмерной структуре пористых материалов.

Цель работы – получение формул геометрических безразмерных коэффициентов прерывистости, просветности и пористости, которые должны содержать функции статистического распределения пор по размерам в поли-размерной структуре пористых материалов.

Материалы и методы

Исследование относится к аналитической разработке методики определения безразмерных параметров пищевых пористых сред. В качестве примера рассмотрен пористый материал, близкий по геометрическим характеристикам типовому пищевому продукту с однородной и изотропной пористой средой, подобной крахмалу, мелкодис- персным пищевым добавкам, муке. Исследование основано на статистическом логнормальном распределении случайных величин и аналитической взаимосвязи между тремя безразмерными интегральными параметрами пористых систем.

Для кубика пористого материала с ребром l коэффициент прерывистости α (в дальнейшем – прерывистость) представляет собой отношение величины отрезка Δ (м), составленного из стянутых в линию всех пор, отнесенную к длине ребра l (м), на которой производится подсчет пор. Коэффициент просветности β (в дальнейшем – просветность) представляет собой отношение величины площади пор S п (м²) к квадратной площади грани кубика S (м²), являющейся счетным полем при экспериментальном построении гистограммы. Коэффициент пористости γ (в дальнейшем – пористость) – это отношение объема стянутых воедино пор кубика V п (м³) к объему кубика V (м³):

α = Δ/ l , β = S п / S , γ = V п / V , б/р.      (1)

Существует теорема об аналитической взаимосвязи между этими тремя коэффициентами [1]. Ею доказывается, что для пористых материалов со статистически упорядоченной, однородной и изотропной пористой системой пор α = γ ^1/3, β = γ ^{2 /3}, γ = α ³ = β ^3/2, б, р. (2)

Для неоднородных и анизотропных сред эти соотношения корректируются [11].

Отметим, что в представленном формулами (1) и (2) виде эти коэффициенты являются числами и отражают интегральные характеристики пористого материала. Требуется преобразовать функции коэффициентов (2) таким образом, чтобы ими можно было бы учитывать в поли-размерной поровой структуре долю влияния пор каждого размера на основе статистического распределения пор по их размерам. Примем без потери общности методики распределение логнормальным [3, 8, 12]. Будем основывать на нем дальнейшие рассуждения, которые могут быть распространены и на пористые системы с нормальным распределением размеров пор.

Логнормальное распределение описывает формула

• 1    ( ln x — In a )

• 1              -7l1

у ( x ) = —^ e ⁽ "  ^J , ^б/Р     (3)

x^j 2 n где параметр x – случайная величина; y(x) – частота распределения параметра x в безразмерных долях; σ – среднеквадратичное отклонение; a – коэффициент.

В (3) все параметры записаны в безразмерном виде для соответствия правой части равенства безразмерной функции y ( x ).

Дальнейшее исследование проводим с использованием примера гистограммы статистического логнормального распределения пор.

В качестве примера имеем:

• •    гистограмму распределения пор по размерам в пористом теле (рисунок 1), близкую к логарифмическому, в безразмерных координатах: x – ось абсцисс, y ( x ) – ось ординат в долях от количества;

• •    всего на квадратном счетном поле количество пор составляет N Σ = 3066 шт.;

рассчитывается по (5) со средним значением b ср i = ( b i + b i + 1 )/2.

Размерную непрерывную аналитическую функцию φ ( b ) получаем с помощью формул (4) и (5), в которых дискретные параметры φ ( b ) i и b i заменяем на текущие φ ( b ) и b . Значит, функция φ ( b ) будет иметь вид

^{ф (} b ) =

с • V2n

• экспериментальное значение пористости

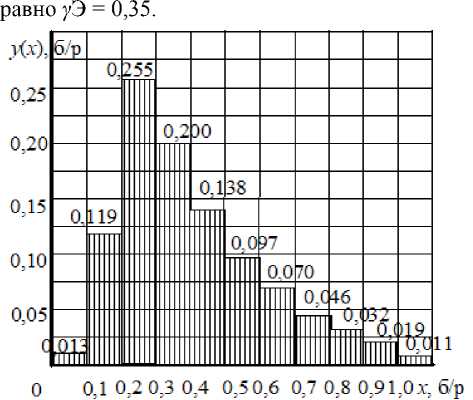
Рисунок 1. Гистограмма частотного распределения пор по характерному размеру: y ( x ), б/ р – доля пор каждого размера; x , б/ р – безразмерный характерный параметр пор

Figure 1. The histogram of the frequency distribution of the pore size characteristic: y ( x ), d/l – the proportion of pores of each size; x , d/l is the dimensionless characteristic parameter

В (6) три константы а 0 , b 1 и σ пока неизвестны. Их определяем с использованием трех характерных точек на ниспадающей кривой гистограммы в координатах φ ( b ) – b : на вершине, посередине и на конце гистограммы. Их координаты А 1 (6,437 · 10^-3; 9,5 · 10^-6), А 2 (4,193 · 10^-3; 18,3 · 10^-6) и А 3 (1,103 · 10^-3; 31,5 · 10^-6) подставляем в (6). В результате получаем три уравнения с тремя неизвестными. Решая их, получаем значения трех неизвестных: а 0 = 1,061 ∙ 10^-5 (м), b 1 = 3,089 ∙ 10^-5 (м) и σ = 0,576 (б/р). Таким образом, формула (6) принимает вид:

3066 • 3,089 •Ю^{- 6   2}

0,576 • V2 n

ln

b

1,06140 " -

0,576

= 0,00656 • e

ln b

1,06140'

0,576

Функция φ ( x ) является первой производной от кумулятивной функции ψ ( b ). Значит, d [ ψ ( b )] = φ ( b ) db и с учетом (7) имеем:

Аналитическая часть

Для определения коэффициентов (2) должны быть известны два размерных параметра: Δ и l . Их следует найти на основании экспериментальной гистограммы (рисунок 1), полученной в результате сканирования поверхности площадью l 2 образца. Для этого по рисунку 1, имеющему безразмерные координаты, должна быть построена гистограмма с размерными координатами осей, где высота прямоугольников φ i ( b ) (м) соответствует величинам отрезков из стянутых в непрерывную прямую пор для каждого размера b i (м). Их значения вычисляем по формулам:

b i = b 1 х i , а 0 i = b 1 а , (4)

φ ( b ) i = y ( b ) i b i N Σ , (5)

где b 1 – пока неизвестная линейная величина, м.

Гистограмма в координатах φ ( b ) – b будет иметь вид, аналогичный показанному на рисунке 1. На нем ордината гистограммы φ ( b ) i

V ( ^b ) =

N= ' b с • *J2n

— b 2

i e

h^b I2

с

db =

— b 2

= 0,00656 i e

ln

b

1,061 • 10 ^{- -}

0,576

db .

Проинтегрированная функция ψ ( b ) соответствует площади, занимаемой всеми порами размеров, меньших b .

Для кубика счетное поле (поле, где считали поры) является квадратным. Значит, сторона, занимаемая для статистически упорядоченной однородной и изотропной системы, является тоже квадратной. Тогда на ней площадь поверхности всех пор от нуля до b max будет равна по (8)

Д™ . = JC" V (b)db = 1,397 - 10 6.     (9)

Вестник ВГУИТ/Proceedings of VSUET, Т. 81, № 2, 2019

По (1) и (2)

a max

^A max l

Прерывистость α по (1) пока не можем

определить, поскольку не знаем в рассматриваемом эксперименте величину длины стороны l квадрата счетного поля. Поэтому прибегнем

к ее расчету с использованием экспериментального

значения пористости γ Э , определение которого является стандартной процедурой. По условию рассматриваемого примера имеем γ Э = 0,35. Поэтому по (10) получаем l = 1,983 • 10 -6 м.

Теперь, зная численное значение l , по (1) и (2) можем получить в общем виде функции α , β , γ и построить по данным примера их графики для пор 0... b .

A a = — l

If ^b max  z,x„     1,983 - IO - ⁶

J_o   v ( b )db    ,

,

A)2    %

7 7 = ^Y

'I S b * ^{( b} )d^b

. It b m‘" v ( b )db V v Jo             7

f b ^ ^{( b} )d^b

3,932 •10 ^{- 12,}

(  [Tb )

f V(b)db

. к^b m” y ( b )db

VN 0o            7

b             ³ 2

f o V ( bW ) 7,798 - 10 - ¹⁸

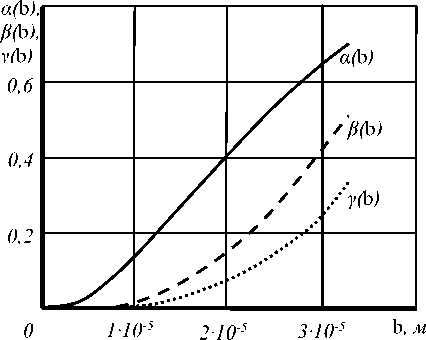
Параметры в (11)–(13) являются безразмерными функциями (рисунок 2).

Результаты и обсуждение

Экспериментальная величина пористости входит в (11)–(13). Она как интегральный параметр является коррелирующей результаты приведенного аналитического решения. Аналогичным образом можно получить формулы, основанные на других типах случайного распределения размеров пор, например, для нормального распределения.

Рассмотренная методика позволяет учитывать долю влияния пор отдельных размерных групп на геометрические параметры, что существенно уточняет вычисления в расчетах тепло- и массообменных процессов пищевых сред.

Рисунок 2. Графики функций α , β и γ , рассчитанные по (11)–(13)

Figure 2. Graphs of functions α , β and γ calculated by (11)–(13)

Заключение

Предложена методика представления трех безразмерных геометрических характеристик пористых материалов в форме статистических функций. Методика позволяет получать формулы для конкретных гистограмм пористых материалов.

Аналитически получены формулы трех безразмерных геометрических параметров пористой среды: прерывистости, просветности и пористости. Ими учитывается статистика случайного распределения характерного размера пор. Формулы включают экспериментальный интегральный параметр пористости, определяемый стандартными методиками. Он корректирует результаты автоматизированного определения распределения размеров пор. Формулы позволяют проводить вычисление влияния отдельных размерных групп пор или всего их размерного ансамбля, что является важным в расчетах тепло-и массообменных процессов в пористых средах.

Данная методика позволяет применять ее в подобных исследованиях для статистических задач различного вида.